Topic how do you solve square root equations: Solving square root equations can be straightforward if you follow a few key steps. This guide will take you through the process of isolating the square root, squaring both sides, solving the resulting equation, and verifying your solutions to ensure accuracy. Let's dive into the methods and examples to help you master solving these equations effectively.
Table of Content
- How to Solve Square Root Equations
- Introduction to Square Root Equations
- Basic Concepts and Terminology
- Step-by-Step Guide to Solving Square Root Equations
- Isolating the Square Root
- Squaring Both Sides of the Equation
- Solving the Resulting Equation
- Checking for Extraneous Solutions
- Common Mistakes to Avoid
- Example Problems and Solutions
- Practice Problems
- Advanced Techniques for Complex Equations
- Using Technology to Solve Square Root Equations
- Applications of Square Root Equations in Real Life
- Conclusion and Summary
- Frequently Asked Questions (FAQ)
- YOUTUBE: Video hướng dẫn cách giải phương trình căn bậc hai một cách chi tiết và dễ hiểu. Thích hợp cho những ai đang tìm kiếm từ khóa 'how do you solve square root equations'.
How to Solve Square Root Equations
Solving square root equations involves isolating the square root on one side of the equation and then squaring both sides to eliminate the square root. Here is a detailed guide on solving square root equations:
Steps to Solve Square Root Equations
-
Isolate the Square Root:
Move all terms with the square root to one side of the equation and other terms to the opposite side. For example, for the equation \(\sqrt{x + 3} = 7\), the square root is already isolated.
-
Square Both Sides:
Square both sides of the equation to eliminate the square root. Continuing with our example:
\(\left(\sqrt{x + 3}\right)^2 = 7^2\)
Which simplifies to:
\(x + 3 = 49\)
-
Solve the Resulting Equation:
Now, solve the equation without the square root. For our example:
Subtract 3 from both sides:
-
Check for Extraneous Solutions:
Substitute the solution back into the original equation to ensure it is valid. In our example, substituting \(x = 46\):
\(\sqrt{46 + 3} = 7\)
\(\sqrt{49} = 7\)
Since this is true, \(x = 46\) is a valid solution.
Example Problems
-
Example 1: Solve \(\sqrt{2x - 5} = 3\)
- Square both sides: \(\left(\sqrt{2x - 5}\right)^2 = 3^2\)
- Simplify: \(2x - 5 = 9\)
- Solve for \(x\): \(2x = 14\)
- Divide by 2: \(x = 7\)
- Check: \(\sqrt{2(7) - 5} = \sqrt{14 - 5} = \sqrt{9} = 3\)
-
Example 2: Solve \(\sqrt{x + 1} + 2 = 5\)
- Isolate the square root: \(\sqrt{x + 1} = 3\)
- Square both sides: \(\left(\sqrt{x + 1}\right)^2 = 3^2\)
- Simplify: \(x + 1 = 9\)
- Solve for \(x\): \(x = 8\)
- Check: \(\sqrt{8 + 1} + 2 = \sqrt{9} + 2 = 3 + 2 = 5\)
Tips and Tricks
- Always isolate the square root term first to make the equation simpler to solve.
- Remember to check for extraneous solutions since squaring both sides can introduce invalid solutions.
- Practice different types of square root equations to become proficient in solving them.
Conclusion
Solving square root equations requires a systematic approach: isolate the square root, square both sides, solve the resulting equation, and check your solutions. With practice, these steps become intuitive, making it easier to handle more complex problems.

READ MORE:
Introduction to Square Root Equations
Square root equations are mathematical expressions that involve the square root of a variable. These equations can often appear complex, but with a systematic approach, they can be simplified and solved. Understanding square root equations is fundamental in various fields of mathematics and its applications.
To solve a square root equation, follow these general steps:
- Isolate the Square Root: If the equation contains a square root, the first step is to isolate the square root term on one side of the equation.
- Square Both Sides: Once the square root is isolated, square both sides of the equation to eliminate the square root. This step may introduce extraneous solutions, so caution is needed.
- Simplify the Equation: After squaring, simplify the resulting equation. This might involve solving a linear or quadratic equation.
- Check for Extraneous Solutions: Always substitute the solutions back into the original equation to check for extraneous solutions. Squaring both sides of an equation can sometimes introduce false solutions that do not satisfy the original equation.
For example, consider the equation \(\sqrt{x} + 3 = 7\). To solve this:
- Isolate the square root: \(\sqrt{x} = 7 - 3\)
- Simplify: \(\sqrt{x} = 4\)
- Square both sides: \(x = 4^2\)
- Simplify: \(x = 16\)
- Check the solution: Substitute \(x = 16\) back into the original equation to verify it is a valid solution.
In more complex cases, such as equations with multiple square roots or additional algebraic terms, the process may involve additional steps like isolating each square root sequentially and squaring multiple times.
By mastering these steps, solving square root equations becomes a manageable and systematic process. Understanding these principles not only aids in solving specific problems but also enhances overall mathematical problem-solving skills.
Basic Concepts and Terminology
Understanding square root equations requires familiarity with some fundamental concepts and terminology. This section will introduce these basics to help you get started.
- Square Root: The square root of a number \(x\) is a number \(y\) such that \(y^2 = x\). It is denoted as \(\sqrt{x}\).
- Radical Symbol: The symbol \(\sqrt{}\) used to denote the square root.
- Radicand: The number under the radical symbol. In \(\sqrt{x}\), \(x\) is the radicand.
- Extraneous Solutions: Solutions that emerge from the process of solving the equation but do not satisfy the original equation when substituted back.
Steps to Solve Square Root Equations
- Isolate the Square Root: Make sure the square root expression is by itself on one side of the equation. For example, in the equation \(\sqrt{x} + 2 = 5\), isolate \(\sqrt{x}\) by subtracting 2 from both sides to get \(\sqrt{x} = 3\).
- Square Both Sides: To eliminate the square root, square both sides of the equation. For \(\sqrt{x} = 3\), squaring both sides gives \(x = 9\).
- Solve the Resulting Equation: After squaring, solve the resulting equation as you would any algebraic equation. This might involve further simplification or solving a quadratic equation.
- Check for Extraneous Solutions: Substitute your solutions back into the original equation to ensure they are valid. This step is crucial because squaring both sides can introduce extraneous solutions.
Example Problem
Consider the equation \(\sqrt{x+3} + 1 = x\). Follow these steps to solve it:
- Isolate the Square Root: Subtract 1 from both sides to get \(\sqrt{x+3} = x - 1\).
- Square Both Sides: Squaring both sides results in \(x + 3 = (x - 1)^2\).
- Solve the Quadratic Equation: Expand and simplify to get \(x + 3 = x^2 - 2x + 1\). Rearrange to form \(x^2 - 3x - 2 = 0\).
- Factor the Quadratic Equation: Factor to get \((x - 2)(x - 1) = 0\). Thus, \(x = 2\) or \(x = 1\).
- Check for Extraneous Solutions: Substitute \(x = 2\) back into the original equation: \(\sqrt{2 + 3} + 1 = 2\) which simplifies to \(\sqrt{5} + 1 \neq 2\), so \(x = 2\) is extraneous. Check \(x = 1\): \(\sqrt{1 + 3} + 1 = 1\) which simplifies to \(\sqrt{4} + 1 = 1\) or \(2 + 1 = 1\), which is also false. Thus, there are no valid solutions.
Step-by-Step Guide to Solving Square Root Equations
Solving square root equations involves isolating the square root term and then eliminating the square root by squaring both sides of the equation. Here is a detailed, step-by-step guide to solving square root equations:
-
Isolate the Square Root
Start by isolating the square root term on one side of the equation. This makes it easier to square both sides later.
-
Square Both Sides of the Equation
Once the square root term is isolated, square both sides of the equation to eliminate the square root. This step is crucial because it transforms the equation into a simpler form that can be solved using standard algebraic techniques.
For example, if your equation is \(\sqrt{2x + 3} = 5\), squaring both sides would give \(2x + 3 = 25\).
-
Simplify and Solve the Resulting Equation
After squaring both sides, you will have a new equation without the square root. Simplify this equation and solve for the variable.
Continuing from the previous example: \(2x + 3 = 25\) simplifies to \(2x = 22\), and then \(x = 11\).
-
Check for Extraneous Solutions
It is important to check your solutions in the original equation. Squaring both sides can introduce extraneous solutions that do not satisfy the original equation.
In the example above, substituting \(x = 11\) back into the original equation \(\sqrt{2x + 3} = 5\) confirms the solution, as \(\sqrt{2 \cdot 11 + 3} = \sqrt{25} = 5\).
By following these steps carefully, you can solve square root equations efficiently and accurately.
Isolating the Square Root
To solve square root equations, the first critical step is to isolate the square root on one side of the equation. This process simplifies the equation and makes it easier to proceed with solving it. Here are the steps to isolate the square root:
-
Identify the square root term: Look for the term that contains the square root. It will usually be in the form of \( \sqrt{expression} \) where "expression" is a mathematical expression that could include variables and constants.
-
Move other terms to the opposite side: Use algebraic operations (addition, subtraction, multiplication, and division) to move all other terms to the opposite side of the equation. The goal is to have the square root term by itself on one side.
For example, in the equation \( \sqrt{2x + 9} - 5 = 0 \), add 5 to both sides to isolate the square root:
\( \sqrt{2x + 9} = 5 \)
-
Ensure the square root is fully isolated: Verify that the square root term is completely isolated. There should be no other terms on the same side of the equation except the square root.
For example, in the equation \( \sqrt{x + 7} + 3 = x \), subtract 3 from both sides to isolate the square root:
\( \sqrt{x + 7} = x - 3 \)
By isolating the square root, you prepare the equation for the next steps, which involve squaring both sides to eliminate the square root and then solving the resulting equation.
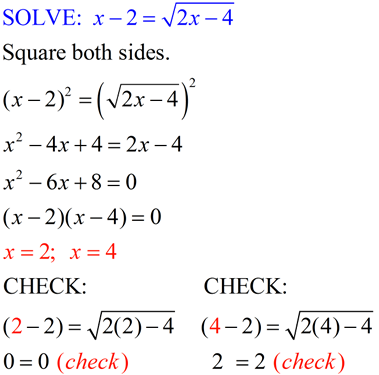
Squaring Both Sides of the Equation
When solving square root equations, one of the crucial steps is to square both sides of the equation to eliminate the square root. This process transforms the equation into a more manageable form. Follow these detailed steps to effectively square both sides:
- Ensure the Square Root is Isolated:
Before squaring, make sure the square root term is by itself on one side of the equation. For example, if your equation is \( \sqrt{2x + 3} = x - 1 \), ensure the square root term \( \sqrt{2x + 3} \) is isolated.
- Square Both Sides:
Once the square root is isolated, square both sides of the equation to eliminate the square root. Using the example above:
\[
(\sqrt{2x + 3})^2 = (x - 1)^2
\]This simplifies to:
\[
2x + 3 = (x - 1)^2
\] - Expand and Simplify:
Next, expand the squared term on the right side. For \( (x - 1)^2 \), this becomes:
\[
2x + 3 = x^2 - 2x + 1
\]Now, rearrange the equation to set it to zero:
\[
2x + 3 - x^2 + 2x - 1 = 0
\]Which simplifies to:
\[
x^2 - 4x - 2 = 0
\] - Solve the Resulting Equation:
At this point, you have a polynomial equation. Use appropriate methods such as factoring, completing the square, or the quadratic formula to solve for \( x \). In this case, you might use the quadratic formula:
\[
x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
\]where \( a = 1 \), \( b = -4 \), and \( c = -2 \).
- Check for Extraneous Solutions:
Squaring both sides can introduce extraneous solutions, which are solutions that do not satisfy the original equation. Always substitute your solutions back into the original equation to verify their validity. If a solution does not satisfy the original equation, discard it.
By following these steps, you can effectively square both sides of a square root equation and solve for the variable while ensuring the solutions are valid.
Solving the Resulting Equation
After squaring both sides of the equation and eliminating the square root, you are left with a more straightforward equation to solve. The steps to solve the resulting equation are as follows:
-
Isolate the variable terms: Move all terms containing the variable to one side of the equation and constant terms to the other side.
Example: If you have the equation \(2x + 9 = 25\), subtract 9 from both sides to isolate the variable term.
\[
2x = 25 - 9 \implies 2x = 16
\] -
Solve for the variable: Once you have isolated the variable terms, solve for the variable by performing the necessary arithmetic operations.
Example: Divide both sides by 2 to solve for \(x\).
\[
x = \frac{16}{2} \implies x = 8
\] -
Verify the solution: Substitute the solution back into the original equation to check if it satisfies the equation. This step is crucial to identify any extraneous solutions introduced during the squaring process.
Example: Substitute \(x = 8\) back into the original equation \(\sqrt{2x + 9} = 5\).
\[
\sqrt{2 \cdot 8 + 9} = 5 \implies \sqrt{16 + 9} = 5 \implies \sqrt{25} = 5 \implies 5 = 5
\]Since both sides are equal, \(x = 8\) is a valid solution.
It's important to perform these steps carefully and check for any possible errors. In some cases, squaring both sides of an equation can introduce extraneous solutions, which do not satisfy the original equation. Always verify your solutions to ensure they are correct.
Checking for Extraneous Solutions
When solving square root equations, it's crucial to verify solutions to ensure they satisfy the original equation. Here’s how to check for extraneous solutions:
- After solving the equation and obtaining potential solutions, substitute each solution back into the original equation.
- Simplify both sides of the equation to verify if the original equation holds true.
- If a substituted solution results in an equation that is true, then it is a valid solution.
- If a substituted solution results in an equation that is false, then it is considered an extraneous solution and should be discarded.
Checking for extraneous solutions ensures that only solutions that are valid within the context of the original equation are considered.
Common Mistakes to Avoid
When solving square root equations, it's crucial to be aware of common mistakes that can lead to incorrect solutions. Here are some key pitfalls to watch out for:
-
Forgetting to Check for Extraneous Solutions
When you square both sides of an equation to eliminate the square root, you can introduce extraneous solutions. Always substitute your solutions back into the original equation to ensure they are valid.
-
Not Isolating the Square Root
Before squaring both sides of the equation, make sure the square root is isolated on one side. This helps to avoid additional complexity and potential mistakes in your calculations.
-
Incorrectly Squaring Both Sides
When squaring both sides of the equation, ensure you apply the operation correctly. Missteps in this process can lead to erroneous results. For example, if you have \(\sqrt{x + 3} = 5\), squaring both sides correctly gives \(x + 3 = 25\).
-
Ignoring Domain Restrictions
Square root functions have domain restrictions, meaning the expression under the square root must be non-negative. Always consider the domain of the original equation to avoid invalid solutions.
-
Mishandling Multiple Square Roots
If your equation contains multiple square roots, isolate and square each one systematically. This may require multiple steps to fully eliminate all square roots from the equation.
-
Assuming All Solutions are Valid
Even if your solutions work mathematically after squaring, they may not be valid for the original equation. Always check each potential solution to confirm it doesn't result in a negative value under a square root or violate other conditions of the problem.
By being mindful of these common mistakes and carefully verifying your solutions, you can avoid errors and accurately solve square root equations.

Example Problems and Solutions
Below are a few example problems with step-by-step solutions to help you understand how to solve square root equations.
Example 1: Simple Square Root Equation
Solve the equation: \(\sqrt{2x + 9} = 5\)
- Isolate the square root: \(\sqrt{2x + 9} = 5\)
- Square both sides: \((\sqrt{2x + 9})^2 = 5^2\)
- Simplify: \(2x + 9 = 25\)
- Subtract 9 from both sides: \(2x = 16\)
- Divide by 2: \(x = 8\)
- Check the solution by substituting \(x = 8\) back into the original equation: \(\sqrt{2(8) + 9} = \sqrt{25} = 5\). The solution is correct.
Example 2: Equation with Two Square Roots
Solve the equation: \(\sqrt{2x - 5} - \sqrt{x - 1} = 1\)
- Isolate one of the square roots: \(\sqrt{2x - 5} = 1 + \sqrt{x - 1}\)
- Square both sides: \((\sqrt{2x - 5})^2 = (1 + \sqrt{x - 1})^2\)
- Simplify: \(2x - 5 = 1 + 2\sqrt{x - 1} + x - 1\)
- Combine like terms: \(2x - 5 = x + 2\sqrt{x - 1}\)
- Isolate the remaining square root: \(x - 5 = 2\sqrt{x - 1}\)
- Square both sides again: \((x - 5)^2 = (2\sqrt{x - 1})^2\)
- Simplify: \(x^2 - 10x + 25 = 4(x - 1)\)
- Expand and simplify: \(x^2 - 10x + 25 = 4x - 4\)
- Combine like terms to form a quadratic equation: \(x^2 - 14x + 29 = 0\)
- Solve the quadratic equation using the quadratic formula: \(x = \frac{14 \pm \sqrt{196 - 116}}{2}\)
- This gives two solutions: \(x = 11.47\) and \(x = 2.53\)
- Check both solutions in the original equation. Only \(x = 11.47\) is valid as \(x = 2.53\) does not satisfy the original equation.
Example 3: Equation Resulting in a Quadratic
Solve the equation: \(\sqrt{x - 4} - \sqrt{x} = -2\)
- Square both sides: \((\sqrt{x - 4} - \sqrt{x})^2 = (-2)^2\)
- Simplify: \((\sqrt{x - 4})^2 - 2\sqrt{(x - 4)x} + (\sqrt{x})^2 = 4\)
- Combine like terms: \(x - 4 - 2\sqrt{x^2 - 4x} + x = 4\)
- Isolate the remaining square root: \(-2\sqrt{x^2 - 4x} = 4 - 2x + 4\)
- Square both sides again: \(4(x^2 - 4x) = (4 - 2x + 4)^2\)
- Simplify to get a quadratic equation: \(4x^2 - 16x = 64 - 16x + 4x^2\)
- Combine like terms and solve the quadratic equation. The solution will be found after verifying valid \(x\) values.
Always remember to check your solutions by substituting them back into the original equation to avoid extraneous solutions.
Practice Problems
Here are some practice problems to help you master solving square root equations. Try to solve these problems step by step and check your solutions to ensure they are correct.
-
Solve for \( x \):
\(\sqrt{3x + 7} = 5\)
- Isolate the square root: \(\sqrt{3x + 7} = 5\)
- Square both sides: \(3x + 7 = 25\)
- Simplify and solve: \(3x = 18\)
\(x = 6\) - Check the solution: \(\sqrt{3(6) + 7} = \sqrt{25} = 5\), which is correct.
-
Solve for \( x \):
\(\sqrt{x + 10} = x - 2\)
- Isolate the square root: \(\sqrt{x + 10} = x - 2\)
- Square both sides: \(x + 10 = (x - 2)^2\)
- Expand and simplify: \(x + 10 = x^2 - 4x + 4\)
- Bring all terms to one side: \(x^2 - 5x - 6 = 0\)
- Factor the quadratic equation: \((x - 6)(x + 1) = 0\)
- Find the solutions: \(x = 6\) or \(x = -1\)
- Check the solutions:
- For \(x = 6\): \(\sqrt{6 + 10} = 6 - 2\)
\(\sqrt{16} = 4\), which is correct. - For \(x = -1\): \(\sqrt{-1 + 10} = -1 - 2\)
\(\sqrt{9} = -3\), which is not correct, so discard \(x = -1\).
- For \(x = 6\): \(\sqrt{6 + 10} = 6 - 2\)
-
Solve for \( x \):
\(\sqrt{2x + 1} + \sqrt{x - 1} = 3\)
- Isolate one square root: \(\sqrt{2x + 1} = 3 - \sqrt{x - 1}\)
- Square both sides: \(2x + 1 = (3 - \sqrt{x - 1})^2\)
- Expand and simplify: \(2x + 1 = 9 - 6\sqrt{x - 1} + x - 1\)
- Combine like terms: \(x + 2 = 9 - 6\sqrt{x - 1}\)
- Isolate the square root: \(6\sqrt{x - 1} = 7 - x\)
- Square both sides again: \(36(x - 1) = (7 - x)^2\)
- Expand and simplify: \(36x - 36 = 49 - 14x + x^2\)
- Bring all terms to one side: \(x^2 - 50x + 85 = 0\)
- Solve the quadratic equation using the quadratic formula: \[ x = \frac{50 \pm \sqrt{50^2 - 4 \cdot 85}}{2} \] \[ x = \frac{50 \pm \sqrt{900}}{2} \] \[ x = \frac{50 \pm 30}{2} \] \[ x = 40 \text{ or } x = 10 \]
- Check the solutions:
- For \(x = 10\): \(\sqrt{2(10) + 1} + \sqrt{10 - 1} = \sqrt{21} + \sqrt{9} \approx 4.58 + 3 = 7.58\), which is not correct.
- For \(x = 40\): \(\sqrt{2(40) + 1} + \sqrt{40 - 1} = \sqrt{81} + \sqrt{39} \approx 9 + 6.24 = 15.24\), which is not correct.
Advanced Techniques for Complex Equations
Solving complex square root equations often requires advanced techniques. Here are some strategies that can help:
-
Isolate the Square Root:
Ensure the square root term is isolated on one side of the equation before proceeding. This helps in simplifying the subsequent steps.
-
Square Both Sides Multiple Times:
When dealing with equations that have multiple square root terms, you may need to square both sides of the equation more than once. For example, for an equation like \( \sqrt{a + \sqrt{b}} = c \), you would square both sides to first isolate \( \sqrt{b} \) and then square again to remove the remaining square root.
- \(\sqrt{a + \sqrt{b}} = c\)
- Square both sides: \( a + \sqrt{b} = c^2 \)
- Isolate the remaining square root: \( \sqrt{b} = c^2 - a \)
- Square both sides again: \( b = (c^2 - a)^2 \)
-
Use Substitution for Complex Radicals:
For equations with nested radicals, use substitution to simplify. Let \( u = \sqrt{b} \), then the equation becomes easier to handle.
- Given: \( \sqrt{x + \sqrt{y}} = z \)
- Let \( u = \sqrt{y} \), then \( \sqrt{x + u} = z \)
- Solve for \( u \): \( x + u = z^2 \)
- Then: \( u = z^2 - x \) and back-substitute to find \( y \)
-
Consider Symmetry and Factorization:
In equations where terms are symmetrical, factorize to simplify the equation. For instance, \( \sqrt{x+3} + \sqrt{x-2} = 5 \) can be squared to make the symmetry more apparent.
- \( \sqrt{x+3} + \sqrt{x-2} = 5 \)
- Square both sides: \( (\sqrt{x+3} + \sqrt{x-2})^2 = 25 \)
- Expand: \( x+3 + 2\sqrt{(x+3)(x-2)} + x-2 = 25 \)
- Combine like terms: \( 2x + 1 + 2\sqrt{(x+3)(x-2)} = 25 \)
- Isolate the square root term: \( 2\sqrt{(x+3)(x-2)} = 24 - 2x \)
- Square both sides again to eliminate the remaining square root.
-
Use the Quadratic Formula:
After removing square roots, the resulting equation is often a quadratic equation. Use the quadratic formula \( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \) to find solutions.
- For \( ax^2 + bx + c = 0 \), identify \( a \), \( b \), and \( c \).
- Calculate the discriminant \( \Delta = b^2 - 4ac \).
- Solve for \( x \) using the quadratic formula.
These advanced techniques can significantly simplify the process of solving complex square root equations and help in finding all possible solutions.
Using Technology to Solve Square Root Equations
Technology can significantly simplify the process of solving square root equations. Here are some tools and techniques you can use:
1. Graphing Calculators
Graphing calculators, such as the TI-84 or Casio FX series, can be used to solve square root equations by plotting the functions and finding the intersection points. Here’s how:
- Enter the equation into the graphing calculator. For example, if you have the equation \( \sqrt{2x+3} = x - 1 \), you can enter \( y_1 = \sqrt{2x+3} \) and \( y_2 = x - 1 \).
- Graph both functions.
- Use the calculator's "Intersect" function to find the point(s) where the graphs intersect, which correspond to the solution(s) of the equation.
2. Computer Algebra Systems (CAS)
Software like Mathematica, Maple, or even online tools like WolframAlpha can solve square root equations symbolically. Here’s an example using WolframAlpha:
- Go to .
- Type the equation into the search bar, e.g., "solve sqrt(2x+3) = x - 1".
- WolframAlpha will provide the solution along with a step-by-step explanation.
3. Online Equation Solvers
Many websites offer tools for solving equations, including square root equations. These tools are easy to use and provide quick results. Some popular options include:
- : Enter the equation and get the solution with steps.
- : Another powerful tool that provides solutions and explanations.
4. Spreadsheet Software
Programs like Microsoft Excel or Google Sheets can be used to solve equations numerically. Here’s a simple method using Excel:
- Set up a column for your variable (e.g., x) and fill it with a range of values.
- In the next column, enter the formula for one side of the equation (e.g., =SQRT(2*A2+3)).
- In another column, enter the formula for the other side of the equation (e.g., =A2-1).
- Look for the row where the values in the two columns are equal. This value of x is your solution.
5. Mobile Apps
There are numerous mobile apps available for solving mathematical equations. Some popular ones include:
- : Simply take a picture of the equation, and the app will solve it and show the steps.
- : Type or take a picture of the equation, and get the solution along with explanations.
By leveraging these technologies, solving square root equations can become a much more manageable and efficient process.

Applications of Square Root Equations in Real Life
Square root equations have numerous practical applications across various fields. Here are some notable examples:
- Geometry and Construction: Square roots are essential in the Pythagorean theorem for calculating distances and angles in right-angled triangles. This principle is widely used in architecture and construction to ensure precise measurements and structural integrity.
- Physics: In physics, square roots are used to calculate the distance between points, the velocity of moving objects, and the kinetic energy of objects. For example, the formula for kinetic energy is \( KE = \frac{1}{2}mv^2 \), where solving for velocity involves taking the square root.
- Finance: Financial analysts use square roots to calculate stock volatility, a measure of how much a stock's price fluctuates over time. This is done by taking the square root of the variance of stock returns to assess investment risk.
- Statistics: Square roots are crucial in statistical analysis for calculating standard deviation, which measures the dispersion of a dataset relative to its mean. The standard deviation is the square root of the variance.
- Engineering: Engineers use square roots to determine the natural frequencies of structures, such as bridges and buildings, to predict how they will respond to different forces and loads. This helps in designing safer and more resilient structures.
- Computer Graphics: In computer graphics, square roots are used to calculate distances and dimensions in 2D and 3D space, essential for rendering images, animations, and simulations.
- Cryptography: Square roots play a role in various cryptographic algorithms used for secure communication and data encryption. These algorithms often involve complex mathematical operations, including square roots, to ensure data security.
- Navigation: Square roots are used to calculate the shortest distance between two points on a map, crucial for navigation in aviation, maritime, and road transportation. This application helps pilots and drivers plot efficient routes.
Understanding and applying square root equations can significantly enhance problem-solving skills and practical knowledge in various real-life scenarios, demonstrating the importance of these mathematical concepts beyond the classroom.
Conclusion and Summary
Solving square root equations is a fundamental skill in algebra that requires careful attention to each step in the process. Here is a summary of the key points:
- Isolating the Square Root: The first step is to isolate the square root term on one side of the equation. This helps to simplify the process of solving the equation.
- Squaring Both Sides: Once the square root is isolated, square both sides of the equation to eliminate the square root. This step transforms the equation into a polynomial equation, which is easier to solve.
- Simplifying the Equation: After squaring both sides, simplify the resulting equation by combining like terms and solving for the variable. This often involves basic algebraic techniques such as factoring or using the quadratic formula.
- Checking for Extraneous Solutions: Not all solutions obtained after squaring both sides are valid. Always substitute the solutions back into the original equation to verify their validity. Discard any extraneous solutions that do not satisfy the original equation.
- Using Advanced Techniques: For more complex equations, advanced techniques such as completing the square or using technology (graphing calculators, algebra software) can be very helpful.
- Applications: Square root equations have real-life applications in various fields, including physics, engineering, and finance. Understanding these applications helps to appreciate the importance of mastering these equations.
In conclusion, solving square root equations involves isolating the square root, squaring both sides, simplifying the resulting equation, and checking for extraneous solutions. By following these steps carefully and using the appropriate techniques, one can solve even the most complex square root equations effectively.
Frequently Asked Questions (FAQ)
-
What is a square root equation?
A square root equation is an equation in which the variable is inside a square root. An example of a simple square root equation is \(\sqrt{x} = 5\).
-
How do you isolate the square root in an equation?
To isolate the square root, move all other terms to the opposite side of the equation. For example, in the equation \(\sqrt{2x + 9} - 5 = 0\), you would add 5 to both sides to get \(\sqrt{2x + 9} = 5\).
-
What is the next step after isolating the square root?
After isolating the square root, square both sides of the equation to eliminate the square root. For example, squaring both sides of \(\sqrt{2x + 9} = 5\) gives \(2x + 9 = 25\).
-
How do you solve the resulting equation after squaring both sides?
After squaring both sides, solve the resulting equation as you would a regular equation. In the example \(2x + 9 = 25\), subtract 9 from both sides to get \(2x = 16\), then divide by 2 to get \(x = 8\).
-
Why do we need to check for extraneous solutions?
Squaring both sides of an equation can introduce extraneous solutions, which are solutions that do not satisfy the original equation. Always substitute your solutions back into the original equation to verify their validity.
-
Can there be more than one square root in an equation?
Yes, equations can have multiple square roots. In such cases, isolate one square root, square both sides to eliminate it, then repeat the process for any remaining square roots.
-
How do you solve an equation with multiple square roots?
To solve an equation with multiple square roots, isolate one square root and square both sides to eliminate it. Continue this process until all square roots are eliminated. For example, in the equation \(\sqrt{2x - 5} - \sqrt{x - 1} = 1\), isolate \(\sqrt{2x - 5}\) and square both sides, then simplify and repeat for the remaining square root.
-
What are some common mistakes to avoid?
Common mistakes include failing to isolate the square root before squaring both sides, forgetting to check for extraneous solutions, and not simplifying the resulting equation correctly.
-
How can technology help in solving square root equations?
Graphing calculators and algebra software can help visualize the solutions and verify their accuracy. Tools like the TI-84 Plus can be used to graph the functions and find the points of intersection, which correspond to the solutions of the equation.
Video hướng dẫn cách giải phương trình căn bậc hai một cách chi tiết và dễ hiểu. Thích hợp cho những ai đang tìm kiếm từ khóa 'how do you solve square root equations'.
Học Cách Giải Phương Trình Căn Bậc Hai
READ MORE:
Video hướng dẫn cách đơn giản hóa căn bậc hai một cách chi tiết và dễ hiểu. Thích hợp cho những ai đang tìm kiếm từ khóa 'how do you solve square root equations'.
Cách Đơn Giản Hóa Căn Bậc Hai









