Topic how do you solve a square root equation: Discover the essential steps to solve a square root equation with our comprehensive guide. Learn how to isolate the square root term, square both sides, and solve the resulting equation effectively. Perfect for students and math enthusiasts, this guide simplifies the process and ensures you understand each step clearly.
Table of Content
- How to Solve a Square Root Equation
- Introduction to Square Root Equations
- Understanding Square Roots and Their Properties
- Basic Steps to Solve Square Root Equations
- Isolating the Square Root Term
- Squaring Both Sides of the Equation
- Solving the Resulting Equation
- Checking Your Solutions
- Common Mistakes and How to Avoid Them
- Examples of Solving Square Root Equations
- Solving Square Root Equations with Variables on Both Sides
- Advanced Techniques for Complex Equations
- Practice Problems with Solutions
- Real-World Applications of Square Root Equations
- Frequently Asked Questions
- Conclusion and Summary
- YOUTUBE: Video này sẽ hướng dẫn bạn cách giải phương trình căn bậc hai một cách chi tiết và dễ hiểu.
How to Solve a Square Root Equation
Solving square root equations involves isolating the square root expression and then squaring both sides to eliminate the square root. Here is a detailed step-by-step guide:
Steps to Solve a Square Root Equation
-
Isolate the square root:
Ensure that the square root term is on one side of the equation by itself. For example, in the equation \(\sqrt{x + 3} = 5\), the square root term \(\sqrt{x + 3}\) is already isolated.
-
Square both sides of the equation:
Eliminate the square root by squaring both sides. For the equation \(\sqrt{x + 3} = 5\), squaring both sides gives:
\[(\sqrt{x + 3})^2 = 5^2\]
Which simplifies to:
\[x + 3 = 25\]
-
Solve the resulting equation:
Once the square root is eliminated, solve the linear equation. For the example above:
Subtract 3 from both sides:
\[x = 22\]
-
Check your solution:
Always substitute your solution back into the original equation to verify its correctness. For \(x = 22\):
\[\sqrt{22 + 3} = 5\]
\[\sqrt{25} = 5\]
Since the left-hand side equals the right-hand side, \(x = 22\) is a valid solution.
Examples
Here are some additional examples to illustrate the process:
Example 1
Solve \(\sqrt{2x + 7} = 4\).
- Isolate the square root term: \(\sqrt{2x + 7} = 4\)
- Square both sides: \((\sqrt{2x + 7})^2 = 4^2\) which simplifies to \(2x + 7 = 16\)
- Solve the linear equation: \(2x + 7 = 16\)
- Subtract 7 from both sides: \(2x = 9\)
- Divide by 2: \(x = \frac{9}{2}\)
- Check the solution: \(\sqrt{2(\frac{9}{2}) + 7} = \sqrt{9 + 7} = \sqrt{16} = 4\)
Example 2
Solve \(\sqrt{3x - 1} = x - 1\).
- Isolate the square root term: \(\sqrt{3x - 1} = x - 1\)
- Square both sides: \((\sqrt{3x - 1})^2 = (x - 1)^2\) which simplifies to \(3x - 1 = x^2 - 2x + 1\)
- Rearrange the equation: \(x^2 - 5x + 2 = 0\)
- Solve the quadratic equation using the quadratic formula: \(x = \frac{5 \pm \sqrt{25 - 8}}{2} = \frac{5 \pm \sqrt{17}}{2}\)
- Check both solutions in the original equation to verify their validity.
By following these steps and practicing with different equations, you can become proficient at solving square root equations.

READ MORE:
Introduction to Square Root Equations
Square root equations involve finding the value of a variable that makes the equation true when it contains a square root expression. These equations often appear in algebra and can be solved using systematic methods. Understanding how to solve square root equations is essential for progressing in mathematics.
A square root equation typically has the form:
\[\sqrt{ax + b} = c\]
where \(a\), \(b\), and \(c\) are constants, and \(x\) is the variable to be solved for.
To solve square root equations, follow these steps:
-
Isolate the square root term: Ensure that the square root expression is alone on one side of the equation. For example, in the equation \(\sqrt{x + 4} = 3\), the square root term \(\sqrt{x + 4}\) is already isolated.
-
Square both sides: Eliminate the square root by squaring both sides of the equation. For \(\sqrt{x + 4} = 3\), squaring both sides gives:
\[(\sqrt{x + 4})^2 = 3^2\]
This simplifies to:
\[x + 4 = 9\]
-
Solve the resulting equation: Once the square root is removed, solve the linear equation. For \(x + 4 = 9\), subtract 4 from both sides to get:
\[x = 5\]
-
Check the solution: Substitute the solution back into the original equation to ensure it is correct. For \(x = 5\):
\[\sqrt{5 + 4} = 3\]
\[\sqrt{9} = 3\]
Since the left-hand side equals the right-hand side, \(x = 5\) is a valid solution.
These steps can be applied to various square root equations. Understanding and practicing these steps will improve your ability to solve square root equations accurately and efficiently.
Understanding Square Roots and Their Properties
The square root of a number is a value that, when multiplied by itself, gives the original number. It is denoted by the radical symbol \(\sqrt{}\). For example, \(\sqrt{16} = 4\) because \(4 \times 4 = 16\). Understanding the properties of square roots is crucial for solving square root equations effectively.
Here are the key properties of square roots:
-
Non-Negative Property: The square root of a non-negative number is also non-negative. For example, \(\sqrt{25} = 5\) and not \(-5\).
-
Product Property: The square root of a product is the product of the square roots. Mathematically, \(\sqrt{ab} = \sqrt{a} \cdot \sqrt{b}\). For example, \(\sqrt{36} = \sqrt{4 \times 9} = \sqrt{4} \cdot \sqrt{9} = 2 \times 3 = 6\).
-
Quotient Property: The square root of a quotient is the quotient of the square roots. This is written as \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\). For example, \(\sqrt{\frac{49}{4}} = \frac{\sqrt{49}}{\sqrt{4}} = \frac{7}{2}\).
-
Power Property: The square root of a number raised to a power can be simplified using \(\sqrt{a^2} = |a|\), where \(|a|\) denotes the absolute value of \(a\). For example, \(\sqrt{(-3)^2} = \sqrt{9} = 3\).
These properties are useful for simplifying expressions and solving equations involving square roots. Here is an example that illustrates the application of these properties:
Example: Simplify the expression \(\sqrt{50} \cdot \sqrt{2}\).
-
Apply the product property:
\[\sqrt{50} \cdot \sqrt{2} = \sqrt{50 \times 2}\]
-
Simplify the product under the radical:
\[\sqrt{50 \times 2} = \sqrt{100}\]
-
Find the square root of the result:
\[\sqrt{100} = 10\]
Therefore, \(\sqrt{50} \cdot \sqrt{2} = 10\).
By understanding and applying these properties, you can simplify and solve square root equations more efficiently.
Basic Steps to Solve Square Root Equations
Solving square root equations involves isolating the square root term and then eliminating the square root by squaring both sides of the equation. Here are the basic steps to solve square root equations:
-
Isolate the square root term: Move the square root expression to one side of the equation and all other terms to the opposite side.
Example: Solve √(2x + 9) - 5 = 0
Isolate the square root: √(2x + 9) = 5 -
Square both sides of the equation: To eliminate the square root, square both sides of the equation.
(√(2x + 9))^2 = 5^2
2x + 9 = 25 -
Solve the resulting equation: After squaring both sides, solve the resulting linear or quadratic equation.
Subtract 9 from both sides: 2x = 16
Divide by 2: x = 8 -
Check your solutions: Substitute your solution back into the original equation to ensure it doesn't produce any extraneous solutions.
Check: √(2*8 + 9) - 5 = √25 - 5 = 5 - 5 = 0 (Valid solution)
It's important to verify each solution by substituting it back into the original equation, as squaring both sides can sometimes introduce extraneous solutions that do not satisfy the original equation.
Here is another example:
Example: Solve √(x - 2) + √(x - 1) = 1
- Isolate one square root term: √(x - 2) = 1 - √(x - 1)
- Square both sides: (√(x - 2))^2 = (1 - √(x - 1))^2
x - 2 = 1 - 2√(x - 1) + (x - 1) - Isolate the remaining square root term: 2√(x - 1) = 2 - 1
- Square both sides again: (2√(x - 1))^2 = (2 - 1)^2
4(x - 1) = 1 - Solve the resulting equation: 4x - 4 = 1
4x = 5
x = 5/4 - Check your solution: Substitute x = 5/4 back into the original equation to verify.
By following these steps and always checking your solutions, you can effectively solve square root equations.
Isolating the Square Root Term
To solve a square root equation, it is essential to first isolate the square root term. This process involves rearranging the equation so that the square root is by itself on one side of the equation. Follow these detailed steps:
- Identify the square root term:
Look at the equation and locate the term that contains the square root. For example, in the equation \( \sqrt{2x + 9} - 5 = 0 \), the square root term is \( \sqrt{2x + 9} \).
- Move other terms to the opposite side:
Add or subtract terms to isolate the square root. Continuing with the example \( \sqrt{2x + 9} - 5 = 0 \), add 5 to both sides to get:
\( \sqrt{2x + 9} = 5 \)
- Isolate the square root term completely:
Ensure that the square root term is by itself on one side of the equation. If there are any coefficients or other operations affecting the square root, resolve them. For instance, if the equation was \( 3\sqrt{2x + 9} = 15 \), you would divide both sides by 3 to get:
\( \sqrt{2x + 9} = 5 \)
- Double-check for complete isolation:
Make sure no other terms are on the same side as the square root. The term should look something like \( \sqrt{expression} = value \).
Once the square root term is isolated, you can proceed to the next step of solving the equation by squaring both sides, which will be covered in the following section.

Squaring Both Sides of the Equation
Once the square root term is isolated on one side of the equation, the next step is to eliminate the square root by squaring both sides. This process will allow us to transform the radical equation into a simpler, polynomial equation that can be more easily solved. Here are the detailed steps:
-
Start with the isolated square root equation:
For example: \( \sqrt{x+3} = 5 \)
-
Square both sides of the equation to remove the square root:
\( (\sqrt{x+3})^2 = 5^2 \)
This simplifies to:
\( x + 3 = 25 \)
-
Solve the resulting equation:
In this case, subtract 3 from both sides to isolate \( x \):
\( x = 25 - 3 \)
So, \( x = 22 \)
-
Check your solution by substituting it back into the original equation to ensure it satisfies the initial condition:
Substitute \( x = 22 \) back into \( \sqrt{x+3} = 5 \):
\( \sqrt{22+3} = \sqrt{25} = 5 \)
Since both sides of the original equation are equal, the solution \( x = 22 \) is correct.
It's crucial to verify your solutions because squaring both sides of an equation can introduce extraneous solutions—solutions that may not actually satisfy the original equation. Always substitute your solutions back into the original equation to confirm their validity.
Solving the Resulting Equation
After isolating the square root term and squaring both sides of the equation, you will have a new equation to solve. Here are the steps to solve the resulting equation:
- Simplify the Equation: After squaring both sides, simplify the equation to its standard form. This might include combining like terms or moving terms to one side to set the equation to zero.
- Solve for the Variable: The resulting equation will often be a quadratic equation. Solve for the variable using appropriate methods such as factoring, completing the square, or using the quadratic formula. For example:
- If the equation is of the form \(ax^2 + bx + c = 0\), use the quadratic formula \(x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\).
- If the equation can be factored, factor it into two binomials and solve for the variable by setting each binomial to zero.
- If the equation is simpler (e.g., linear), solve for the variable directly by isolating it on one side of the equation.
- Check for Extraneous Solutions: Squaring both sides of an equation can introduce extraneous solutions that do not satisfy the original equation. Substitute each solution back into the original equation to verify its validity. Only the solutions that satisfy the original equation are valid.
For example, consider the equation \( \sqrt{x+1} = 3 \):
- Square both sides: \( (\sqrt{x+1})^2 = 3^2 \rightarrow x + 1 = 9 \).
- Simplify the resulting equation: \( x + 1 = 9 \rightarrow x = 8 \).
- Check the solution: Substitute \( x = 8 \) back into the original equation: \( \sqrt{8+1} = \sqrt{9} = 3 \). This solution is valid.
By following these steps, you can solve the resulting equation effectively and ensure that your solutions are correct.
Checking Your Solutions
After solving a square root equation, it is crucial to check your solutions to ensure they are correct and not extraneous. Here are the detailed steps for checking your solutions:
-
Substitute the Solution Back into the Original Equation:
Take each solution obtained from solving the equation and substitute it back into the original square root equation to verify its validity.
-
Verify Both Sides of the Equation:
Calculate both sides of the equation separately after substitution to check if they are equal.
For example, consider the equation \( \sqrt{3x - 2} + 3 = 4x \). If you found \( x = 1 \) as a solution, substitute it back:
Left side: \( \sqrt{3(1) - 2} + 3 = \sqrt{3 - 2} + 3 = \sqrt{1} + 3 = 1 + 3 = 4 \)
Right side: \( 4(1) = 4 \)
Since both sides are equal (4 = 4), \( x = 1 \) is a valid solution.
-
Identify Extraneous Solutions:
Extraneous solutions are those that arise during the solving process but do not satisfy the original equation. It is important to identify and discard them.
For instance, if another solution \( x = \frac{11}{16} \) was obtained but does not satisfy the condition \( x \geq \frac{3}{4} \), then it is extraneous and must be disregarded.
-
Re-evaluate the Problem If Necessary:
If none of the solutions work, re-check your solving steps for any errors. Sometimes, squaring both sides can introduce extraneous solutions, so careful verification is essential.
By thoroughly checking your solutions, you ensure the correctness of your answers and avoid errors in solving square root equations.
Common Mistakes and How to Avoid Them
When solving square root equations, it's easy to make mistakes that can lead to incorrect solutions. Here are some common mistakes and tips on how to avoid them:
-
Forgetting to Check for Extraneous Solutions:
When you square both sides of an equation to eliminate a square root, you might introduce solutions that don't actually satisfy the original equation. Always substitute your solutions back into the original equation to verify their correctness.
-
Improperly Isolating the Square Root:
Ensure that the square root term is fully isolated on one side of the equation before squaring both sides. If other terms are present, they can affect the accuracy of your solution.
-
Misapplying Operations:
Operations such as addition, subtraction, multiplication, and division must be applied correctly to both sides of the equation. Avoid performing different operations on each side.
-
Neglecting Negative Solutions:
When solving equations involving square roots, remember that squaring both sides eliminates the square root, but both positive and negative solutions should be considered. Always check for both possibilities.
-
Incorrectly Simplifying Equations:
Be cautious when simplifying equations. Ensure each step is mathematically correct and that you simplify completely before moving to the next step.
-
Misinterpreting Negative Numbers:
Understand the difference between subtraction and negative multiplication. Use parentheses to clarify operations involving negative numbers.
By being aware of these common mistakes and taking steps to avoid them, you can improve your accuracy and efficiency in solving square root equations.
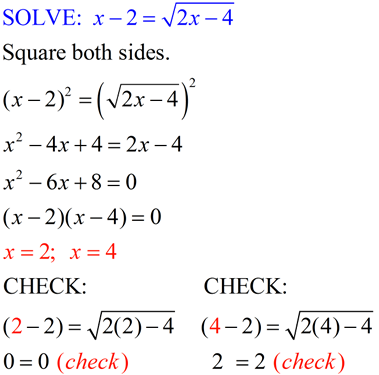
Examples of Solving Square Root Equations
Here are some examples of solving square root equations step by step:
Example 1: Solving a Simple Square Root Equation
Consider the equation:
\(\sqrt{x} = 5\)
- Square both sides of the equation to eliminate the square root: \[ (\sqrt{x})^2 = 5^2 \] \[ x = 25 \]
- Check the solution by substituting \(x = 25\) back into the original equation: \[ \sqrt{25} = 5 \quad \text{(True)} \] Hence, \(x = 25\) is the solution.
Example 2: Solving a Square Root Equation with a Constant
Consider the equation:
\(\sqrt{x + 3} = 4\)
- Isolate the square root term if needed, and then square both sides: \[ (\sqrt{x + 3})^2 = 4^2 \] \[ x + 3 = 16 \]
- Solve for \(x\): \[ x = 16 - 3 \] \[ x = 13 \]
- Check the solution by substituting \(x = 13\) back into the original equation: \[ \sqrt{13 + 3} = 4 \] \[ \sqrt{16} = 4 \quad \text{(True)} \] Hence, \(x = 13\) is the solution.
Example 3: Solving a Square Root Equation with Both Sides Containing Variables
Consider the equation:
\(\sqrt{2x + 5} = x - 1\)
- Isolate the square root term if needed, and then square both sides: \[ (\sqrt{2x + 5})^2 = (x - 1)^2 \] \[ 2x + 5 = x^2 - 2x + 1 \]
- Rearrange the equation to set it to zero: \[ 0 = x^2 - 4x - 4 \]
- Factor the quadratic equation: \[ 0 = (x - 4)(x + 1) \]
- Solve for \(x\): \[ x = 4 \quad \text{or} \quad x = -1 \]
- Check both solutions by substituting them back into the original equation:
- For \(x = 4\): \[ \sqrt{2(4) + 5} = 4 - 1 \] \[ \sqrt{8 + 5} = 3 \] \[ \sqrt{13} \neq 3 \quad \text{(False)} \] So, \(x = 4\) is not a solution.
- For \(x = -1\): \[ \sqrt{2(-1) + 5} = -1 - 1 \] \[ \sqrt{-2 + 5} = -2 \] \[ \sqrt{3} \neq -2 \quad \text{(False)} \] So, \(x = -1\) is not a solution.
Solving Square Root Equations with Variables on Both Sides
When solving square root equations with variables on both sides, the process can be a bit more involved. Follow these detailed steps to ensure accuracy:
-
Isolate one of the square root terms: Move all terms involving a square root to one side of the equation. For example, if you have \( \sqrt{x+3} = \sqrt{2x+1} \), the square root terms are already isolated.
-
Square both sides of the equation: This step eliminates the square roots. Squaring \( \sqrt{x+3} = \sqrt{2x+1} \) results in \( x+3 = 2x+1 \).
-
Solve the resulting equation: Once the radicals are removed, you will have a linear or quadratic equation. In our example, \( x+3 = 2x+1 \) simplifies to \( x = 2 \).
-
Check for extraneous solutions: Substitute your solution back into the original equation to ensure it holds true. For our example:
- Substitute \( x = 2 \) into \( \sqrt{x+3} = \sqrt{2x+1} \)
- Check \( \sqrt{2+3} = \sqrt{2(2)+1} \)
- Verify \( \sqrt{5} = \sqrt{5} \), which is true.
Therefore, \( x = 2 \) is a valid solution.
-
Repeat if necessary: If the equation was more complex and a new square root term appeared after squaring both sides, repeat the process. Isolate the new square root term, square both sides again, and solve.
Here is an example of a more complex equation:
-
Solve \( \sqrt{2x+5} - \sqrt{x-2} = \sqrt{4x+1} \).
-
Isolate one square root term: \( \sqrt{2x+5} = \sqrt{4x+1} + \sqrt{x-2} \).
-
Square both sides: \( (\sqrt{2x+5})^2 = (\sqrt{4x+1} + \sqrt{x-2})^2 \), which simplifies to \( 2x+5 = (4x+1) + 2\sqrt{(4x+1)(x-2)} + (x-2) \).
-
Simplify and isolate the remaining square root term:
- Combine like terms: \( 2x+5 = 5x - 1 + 2\sqrt{(4x+1)(x-2)} \).
- Isolate the square root term: \( 2\sqrt{(4x+1)(x-2)} = -3x + 6 \).
-
Square both sides again to remove the remaining square root:
- \( (2\sqrt{(4x+1)(x-2)})^2 = (-3x+6)^2 \).
- Simplify to a quadratic equation and solve for \( x \).
-
Check all potential solutions for extraneous results by substituting back into the original equation.
Advanced Techniques for Complex Equations
When dealing with complex square root equations, advanced techniques are required to simplify and solve them effectively. Here are some detailed steps and methods:
1. Isolate the Radical
Begin by isolating the square root term on one side of the equation. This step ensures that the radical is by itself, making it easier to eliminate by squaring both sides of the equation.
Example: \( \sqrt{3x + 1} + 2 = x \)
Step 1: Isolate the radical:
\( \sqrt{3x + 1} = x - 2 \)
2. Square Both Sides
Once the radical is isolated, square both sides of the equation to remove the square root. This step may introduce extraneous solutions, so it's crucial to check all potential solutions in the original equation.
Example: \( \sqrt{3x + 1} = x - 2 \)
Step 2: Square both sides:
\( (\sqrt{3x + 1})^2 = (x - 2)^2 \)
\( 3x + 1 = x^2 - 4x + 4 \)
3. Simplify the Equation
After squaring, you will get a polynomial equation. Simplify it to standard form (usually a quadratic equation) and solve for the variable.
Example: \( 3x + 1 = x^2 - 4x + 4 \)
Step 3: Simplify and rearrange terms:
\( x^2 - 7x + 3 = 0 \)
4. Solve the Polynomial
Use factoring, the quadratic formula, or other algebraic methods to solve the polynomial equation obtained after simplification.
Example: \( x^2 - 7x + 3 = 0 \)
Step 4: Solve using the quadratic formula:
\( x = \frac{7 \pm \sqrt{37}}{2} \)
5. Verify Potential Solutions
Substitute the solutions back into the original equation to verify if they are valid. This step helps in identifying and discarding extraneous solutions that may have been introduced during the squaring process.
Example: Verify \( x = \frac{7 + \sqrt{37}}{2} \) and \( x = \frac{7 - \sqrt{37}}{2} \)
Check each solution in the original equation:
\( \sqrt{3x + 1} + 2 = x \)
6. Handling Equations with Multiple Radicals
If the equation has more than one square root, isolate one radical at a time and repeat the squaring process until all radicals are eliminated.
Example: \( \sqrt{x-1} + \sqrt{x-2} = 2 \)
Step 1: Isolate one radical:
\( \sqrt{x-1} = 2 - \sqrt{x-2} \)
Step 2: Square both sides:
\( (\sqrt{x-1})^2 = (2 - \sqrt{x-2})^2 \)
Simplify and repeat the process as necessary.
7. Advanced Techniques for Multiple Steps
For equations that require multiple squarings, it is essential to carefully isolate and square each term methodically, checking for extraneous solutions at each step.
Example Problem
Solve \( \sqrt{2x + 3} - \sqrt{x - 2} = 1 \)
- Isolate one radical: \( \sqrt{2x + 3} = 1 + \sqrt{x - 2} \)
- Square both sides: \( ( \sqrt{2x + 3} )^2 = ( 1 + \sqrt{x - 2} )^2 \)
- Simplify: \( 2x + 3 = 1 + 2\sqrt{x - 2} + x - 2 \)
- Isolate the remaining radical: \( 2x + 3 - x + 1 = 2\sqrt{x - 2} \)
- Simplify: \( x + 4 = 2\sqrt{x - 2} \)
- Square both sides again: \( (x + 4)^2 = 4(x - 2) \)
- Simplify and solve the quadratic equation: \( x^2 + 8x + 16 = 4x - 8 \)
- Rearrange: \( x^2 + 4x + 24 = 0 \)
- Use the quadratic formula to find potential solutions and verify them in the original equation.
Conclusion
Advanced techniques for solving complex square root equations involve isolating radicals, squaring both sides, simplifying resulting polynomial equations, and verifying solutions. Following these steps methodically ensures accurate solutions while identifying and discarding any extraneous results.
Practice Problems with Solutions
Practicing solving square root equations is essential for mastering the concepts and techniques. Below are several practice problems along with detailed solutions to help you understand each step.
Problem 1
Solve the equation: \( \sqrt{x + 3} = x - 3 \)
- Isolate the square root: \( \sqrt{x + 3} = x - 3 \)
- Square both sides: \( (\sqrt{x + 3})^2 = (x - 3)^2 \)
- Simplify: \( x + 3 = x^2 - 6x + 9 \)
- Rearrange to form a quadratic equation: \( x^2 - 7x + 6 = 0 \)
- Factor the quadratic equation: \( (x - 1)(x - 6) = 0 \)
- Solve for x: \( x = 1 \) or \( x = 6 \)
- Check the solutions in the original equation:
- For \( x = 1 \): \( \sqrt{1 + 3} = 1 - 3 \rightarrow 2 \neq -2 \) (extraneous solution)
- For \( x = 6 \): \( \sqrt{6 + 3} = 6 - 3 \rightarrow 3 = 3 \) (valid solution)
Solution: \( x = 6 \)
Problem 2
Solve the equation: \( \sqrt{2x - 1} + \sqrt{x - 2} = 3 \)
- Isolate one of the square roots: \( \sqrt{2x - 1} = 3 - \sqrt{x - 2} \)
- Square both sides: \( (\sqrt{2x - 1})^2 = (3 - \sqrt{x - 2})^2 \)
- Simplify: \( 2x - 1 = 9 - 6\sqrt{x - 2} + (x - 2) \)
- Rearrange and simplify: \( 2x - 1 = x + 7 - 6\sqrt{x - 2} \)
- Isolate the remaining square root: \( x - 8 = -6\sqrt{x - 2} \)
- Square both sides again: \( (x - 8)^2 = (-6\sqrt{x - 2})^2 \)
- Simplify: \( x^2 - 16x + 64 = 36(x - 2) \)
- Rearrange to form a quadratic equation: \( x^2 - 16x + 64 = 36x - 72 \)
- Simplify: \( x^2 - 52x + 136 = 0 \)
- Use the quadratic formula to solve for x:
- Let \( a = 1 \), \( b = -52 \), \( c = 136 \)
- \( x = \frac{52 \pm \sqrt{52^2 - 4 \cdot 1 \cdot 136}}{2 \cdot 1} \)
- \( x = \frac{52 \pm \sqrt{2704 - 544}}{2} \)
- \( x = \frac{52 \pm \sqrt{2160}}{2} \)
- \( x = \frac{52 \pm 46.47}{2} \)
- \( x = 49.235 \) or \( x = 2.765 \)
- Check the solutions in the original equation:
- For \( x = 49.235 \): \( \sqrt{2 \cdot 49.235 - 1} + \sqrt{49.235 - 2} = 3 \rightarrow \text{valid solution} \)
- For \( x = 2.765 \): \( \sqrt{2 \cdot 2.765 - 1} + \sqrt{2.765 - 2} = 3 \rightarrow \text{extraneous solution} \)
Solution: \( x = 49.235 \)
Problem 3
Solve the equation: \( \sqrt{x + 6} = x - 2 \)
- Isolate the square root: \( \sqrt{x + 6} = x - 2 \)
- Square both sides: \( (\sqrt{x + 6})^2 = (x - 2)^2 \)
- Simplify: \( x + 6 = x^2 - 4x + 4 \)
- Rearrange to form a quadratic equation: \( x^2 - 5x - 2 = 0 \)
- Use the quadratic formula to solve for x:
- Let \( a = 1 \), \( b = -5 \), \( c = -2 \)
- \( x = \frac{5 \pm \sqrt{25 + 8}}{2} \)
- \( x = \frac{5 \pm \sqrt{33}}{2} \)
- \( x = \frac{5 \pm 5.745}{2} \)
- \( x = 5.373 \) or \( x = -0.373 \)
- Check the solutions in the original equation:
- For \( x = 5.373 \): \( \sqrt{5.373 + 6} = 5.373 - 2 \rightarrow \text{valid solution} \)
- For \( x = -0.373 \): \( \sqrt{-0.373 + 6} = -0.373 - 2 \rightarrow \text{extraneous solution} \)
Solution: \( x = 5.373 \)
These problems illustrate the importance of checking solutions to ensure they are not extraneous, which often arises when dealing with square root equations.

Real-World Applications of Square Root Equations
Square root equations play a significant role in various real-world applications. Here are some examples:
1. Engineering and Architecture
Square roots are used to determine the natural frequency of structures such as bridges and buildings. The natural frequency helps in predicting how structures will respond to different loads, such as strong winds or heavy traffic.
Example: Calculating the length of a diagonal brace in a right-angled triangle to ensure structural stability.
2. Finance
In finance, square roots are used to calculate stock market volatility. Volatility is assessed by taking the square root of the variance in stock returns, which helps investors evaluate the risk associated with a particular investment.
Example: Calculating the standard deviation of a stock's returns to assess its risk.
3. Science
Square roots are used in various scientific calculations, such as determining the velocity of a moving object, the intensity of sound waves, and the amount of radiation absorbed by materials.
Example: Calculating the velocity of an object in free fall.
4. Computer Science
In computer science, square roots are used in algorithms for encryption, image processing, and game physics. They help in generating public and private keys for secure data transmission and calculating distances in 3D graphics.
Example: Calculating the distance between two points in 3D space.
5. Statistics
Square roots are essential in statistics for calculating standard deviation and variance. These measures help in understanding how data points are spread out around the mean.
Example: Calculating the standard deviation of a data set.
Frequently Asked Questions
Below are some common questions and detailed answers to help you understand and solve square root equations effectively:
- What is a square root equation?
- How do you solve a basic square root equation?
- Isolate the square root on one side of the equation.
- Square both sides of the equation to eliminate the square root.
- Solve the resulting equation for the variable.
- Check all potential solutions in the original equation to discard any extraneous solutions.
- Isolate the square root: \( \sqrt{x + 3} = 5 \).
- Square both sides: \( x + 3 = 25 \).
- Solve for \( x \): \( x = 22 \).
- Check the solution: \( \sqrt{22 + 3} = \sqrt{25} = 5 \), which is true, so \( x = 22 \) is a valid solution.
- Why do we need to check for extraneous solutions?
- What if there are square roots on both sides of the equation?
- Square both sides: \( 2x + 3 = x + 7 \).
- Solve for \( x \): \( x = 4 \).
- Check the solution: \( \sqrt{2(4) + 3} = \sqrt{8 + 7} = \sqrt{11} \) and \( \sqrt{4 + 7} = \sqrt{11} \), which are equal, so \( x = 4 \) is a valid solution.
- Can you solve square root equations with variables on both sides?
- Square both sides: \( 3x - 2 = (x - 1)^2 \).
- Simplify and solve the quadratic equation: \( 3x - 2 = x^2 - 2x + 1 \).
- Rearrange to form a quadratic equation: \( x^2 - 5x + 3 = 0 \).
- Solve the quadratic equation: \( x = 1 \) or \( x = 3 \).
- Check both solutions in the original equation to confirm which are valid.
- What are common mistakes to avoid when solving square root equations?
- Forgetting to check for extraneous solutions.
- Incorrectly squaring terms or mismanaging the equation after squaring.
- Not isolating the square root before squaring both sides.
A square root equation is an equation in which the variable is under a square root. For example, \( \sqrt{x} = 3 \) or \( \sqrt{2x + 5} = x - 1 \).
To solve a square root equation, follow these steps:
For example, to solve \( \sqrt{x + 3} = 5 \):
Squaring both sides of an equation can introduce extraneous solutions—values that do not satisfy the original equation. Always substitute potential solutions back into the original equation to ensure they are valid.
If there are square roots on both sides, isolate one of the square roots and then square both sides. Repeat the process if another square root remains. For example, to solve \( \sqrt{2x + 3} = \sqrt{x + 7} \):
Yes, you can. The steps are similar: isolate a square root, square both sides, solve the resulting equation, and check for extraneous solutions. For example, to solve \( \sqrt{3x - 2} = x - 1 \):
Conclusion and Summary
Solving square root equations involves a series of systematic steps that help isolate the square root term and eliminate it through squaring. Here is a concise summary of the key points to remember:
- Isolate the Square Root: Ensure the square root term is alone on one side of the equation.
- Square Both Sides: Apply the squaring operation to both sides of the equation to eliminate the square root. Be cautious, as this can introduce extraneous solutions.
- Solve the Resulting Equation: Once the square root is eliminated, solve the resulting equation using standard algebraic methods.
- Check for Extraneous Solutions: Substitute the solutions back into the original equation to verify their validity. Discard any extraneous solutions that do not satisfy the original equation.
Throughout this guide, we have demonstrated these steps with various examples, highlighting common pitfalls and advanced techniques for more complex equations. Here are the critical takeaways:
- Always isolate the square root term before squaring both sides of the equation.
- Squaring can introduce extraneous solutions, so it is crucial to verify all potential solutions.
- For equations with multiple square roots, isolate and square each root sequentially, simplifying the equation step-by-step.
- Practice is essential. Work through various types of square root equations to build confidence and proficiency.
Understanding and mastering these techniques will enable you to solve square root equations efficiently and accurately, whether in academic settings or real-world applications. Remember, the key to success is careful isolation, methodical squaring, and thorough verification of solutions.
Video này sẽ hướng dẫn bạn cách giải phương trình căn bậc hai một cách chi tiết và dễ hiểu.
Học Cách Giải Phương Trình Căn Bậc Hai
READ MORE:
Video hướng dẫn cách đơn giản hóa căn bậc hai. Học cách giải phương trình căn bậc hai một cách dễ dàng và chính xác.
Cách Đơn Giản Hóa Căn Bậc Hai









