Topic how do you simplify a square root: Simplifying square roots can seem challenging, but with a few simple steps, it becomes much easier. This guide will show you how to break down square roots into their simplest forms, using methods like prime factorization and recognizing perfect squares. Master these techniques to simplify any square root efficiently and accurately.
Table of Content
- Simplifying Square Roots
- Introduction to Simplifying Square Roots
- Basic Rules for Simplifying Square Roots
- Examples of Simplifying Square Roots
- Using Prime Factorization to Simplify Square Roots
- Simplifying Square Roots of Fractions
- Simplifying Square Roots with Variables
- Advanced Examples and Special Cases
- Common Mistakes and How to Avoid Them
- Practice Problems and Solutions
- Conclusion
- YOUTUBE:
Simplifying Square Roots
Simplifying a square root involves expressing it in the simplest radical form. This often means finding and extracting perfect square factors.
Steps to Simplify a Square Root
- Factor the number inside the square root into its prime factors.
- Identify and separate the perfect squares from the factors.
- Take the square root of the perfect squares and move them outside the radical sign.
- Multiply the numbers outside the radical sign.
- Simplify the expression inside the radical if necessary.
Examples
Example 1: Simplify √12
First, factor 12 into 4 and 3:
\[\sqrt{12} = \sqrt{4 \times 3}\]
Then, use the property of square roots:
\[\sqrt{4 \times 3} = \sqrt{4} \times \sqrt{3} = 2\sqrt{3}\]
So, √12 simplifies to 2√3.
Example 2: Simplify √45
Factor 45 into 9 and 5:
\[\sqrt{45} = \sqrt{9 \times 5}\]
Then, simplify:
\[\sqrt{9 \times 5} = \sqrt{9} \times \sqrt{5} = 3\sqrt{5}\]
So, √45 simplifies to 3√5.
Example 3: Simplify √72
Factor 72 into 36 and 2:
\[\sqrt{72} = \sqrt{36 \times 2}\]
Then, simplify:
\[\sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} = 6\sqrt{2}\]
So, √72 simplifies to 6√2.
Simplifying Fractions Under a Square Root
To simplify the square root of a fraction, use the quotient property:
\[\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\]
Example: Simplify \(\sqrt{\frac{72z^{12}}{2z^{10}}}\)
First, simplify the fraction inside the radical:
\[\sqrt{\frac{72z^{12}}{2z^{10}}} = \sqrt{36z^{2}} = 6z\]
Example: Simplify \(\sqrt{\frac{21}{64}}\)
Rewrite using the quotient property:
\[\sqrt{\frac{21}{64}} = \frac{\sqrt{21}}{\sqrt{64}} = \frac{\sqrt{21}}{8}\]
Example: Simplify \(\sqrt{\frac{80m^3}{n^6}}\)
Rewrite and simplify:
\[\sqrt{\frac{80m^3}{n^6}} = \frac{\sqrt{80m^3}}{\sqrt{n^6}} = \frac{4m\sqrt{5m}}{n^3}\]
Combining Like Square Roots
Like square roots have the same quantity under the radical sign and can be combined by adding or subtracting the coefficients.
Example: Combine \(2\sqrt{3}\) and \(5\sqrt{3}\)
\(2\sqrt{3} + 5\sqrt{3} = (2+5)\sqrt{3} = 7\sqrt{3}\)
Example: Combine \(4\sqrt{2}\) and \(-3\sqrt{2}\)
\(4\sqrt{2} - 3\sqrt{2} = (4-3)\sqrt{2} = 1\sqrt{2} = \sqrt{2}\)

READ MORE:
Introduction to Simplifying Square Roots
Simplifying square roots involves breaking down a radical expression into its simplest form. This process makes the number inside the square root as small as possible while ensuring it remains a whole number. Here are the key steps:
- Factor the number inside the square root into its prime factors.
- Group the prime factors into pairs.
- Move one of each pair of factors outside the square root.
- Multiply the factors outside the square root and keep the remaining factors inside.
Let's look at some examples to illustrate these steps:
- Simplify
$$\sqrt{12}$$ :
- Factor 12 into primes: \(12 = 2 \times 2 \times 3\)
- Pair the factors: \(2\)
- Move one 2 outside: \(\sqrt{12} = 2\sqrt{3}\)
- Simplify
$$\sqrt{45}$$ :
- Factor 45 into primes: \(45 = 3 \times 3 \times 5\)
- Pair the factors: \(3\)
- Move one 3 outside: \(\sqrt{45} = 3\sqrt{5}\)
This method can also be applied to more complex expressions involving variables and fractions. For instance:
- Simplify
$$\sqrt{\frac{72z^{12}}{2z^{10}}}$$ :
- Simplify the fraction: \(\frac{72z^{12}}{2z^{10}} = 36z^2\)
- Apply the square root to each part: \(\sqrt{36z^2} = 6z\)
- Simplify
$$\sqrt{\frac{45x^5}{y^4}}$$ :
- Rewrite using the quotient property: \(\frac{\sqrt{45x^5}}{\sqrt{y^4}}\)
- Simplify each radical: \(\frac{3x^2\sqrt{5x}}{y^2}\)
By following these steps, you can simplify square roots effectively and make calculations easier to handle.
Basic Rules for Simplifying Square Roots
Simplifying square roots involves reducing the number inside the radical sign to its simplest form. Here are the basic rules to follow:
- Identify Perfect Squares: Look for factors of the number that are perfect squares (e.g., 4, 9, 16, 25).
- Rewrite the Square Root: Express the square root as the product of square roots of its factors.
- Simplify the Square Root: Take the square root of the perfect square factor to simplify.
For example, to simplify \( \sqrt{18} \):
- Identify factors: \( 18 = 9 \times 2 \).
- Rewrite the square root: \( \sqrt{18} = \sqrt{9 \times 2} \).
- Apply the product rule: \( \sqrt{9} \times \sqrt{2} \).
- Simplify: \( 3\sqrt{2} \), since \( \sqrt{9} = 3 \).
Here is another example, simplifying \( \sqrt{50} \):
- Identify factors: \( 50 = 25 \times 2 \).
- Rewrite the square root: \( \sqrt{50} = \sqrt{25 \times 2} \).
- Apply the product rule: \( \sqrt{25} \times \sqrt{2} \).
- Simplify: \( 5\sqrt{2} \), since \( \sqrt{25} = 5 \).
When simplifying square roots with variables, use the same principles:
- For \( \sqrt{x^2 \times y} \), simplify to \( x\sqrt{y} \).
Understanding these basic rules helps in simplifying more complex expressions involving square roots.
Examples of Simplifying Square Roots
Here are some examples illustrating how to simplify square roots:
- Simplify \( \sqrt{36} \):
- Simplify \( \sqrt{50} \):
- Simplify \( \sqrt{72} \):
- Simplify \( \sqrt{98} \):
- Simplify \( \sqrt{162} \):
\( \sqrt{36} = 6 \) because \( 6 \times 6 = 36 \).
\( \sqrt{50} = \sqrt{25 \times 2} = 5\sqrt{2} \) by breaking down 50 into factors of 25 and 2.
\( \sqrt{72} = \sqrt{36 \times 2} = 6\sqrt{2} \) using the square root of 36 and simplifying further.
\( \sqrt{98} = \sqrt{49 \times 2} = 7\sqrt{2} \) by factoring 98 into 49 and 2.
\( \sqrt{162} = \sqrt{81 \times 2} = 9\sqrt{2} \) simplifying with the square root of 81.
Using Prime Factorization to Simplify Square Roots
Prime factorization is a useful method for simplifying square roots. Here are the steps:
- Identify the prime factors of the number inside the square root.
- Pair up identical factors that are inside the square root sign.
- Take one factor from each pair outside the square root sign.
- If there's an unpaired factor left inside the square root, leave it there.
- Combine any like terms that are outside the square root.
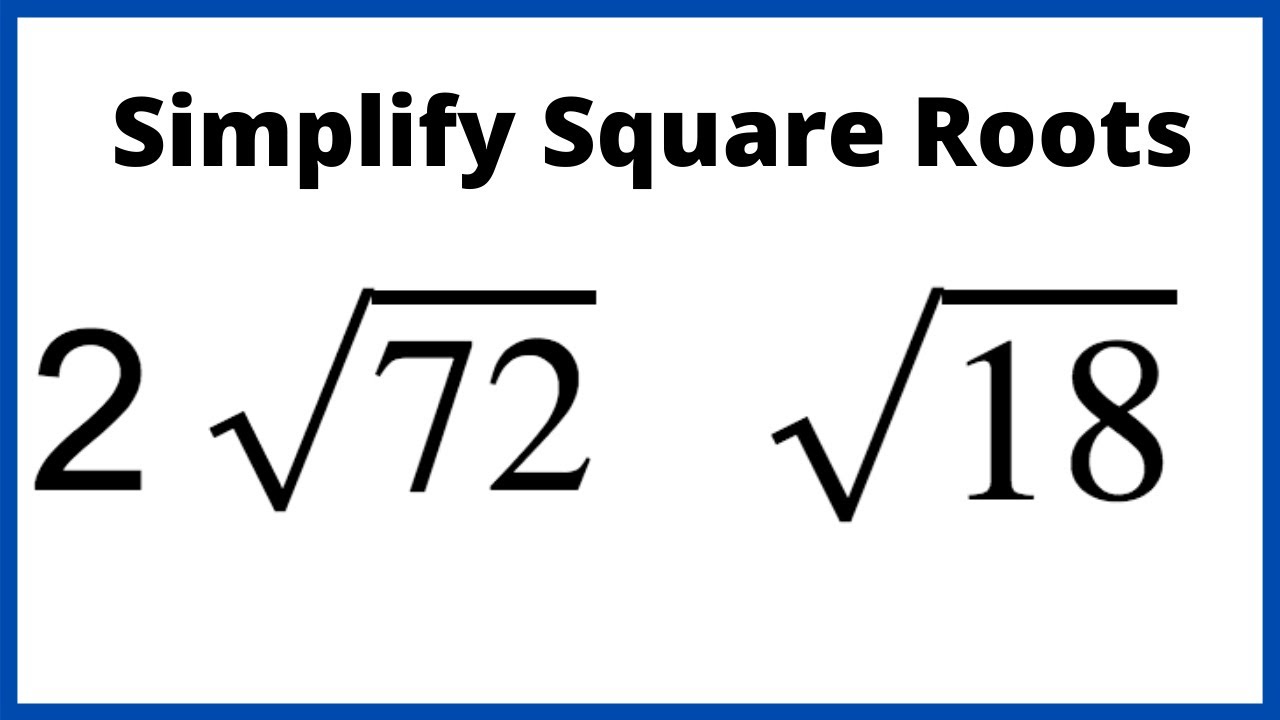
Simplifying Square Roots of Fractions
Here’s how to simplify square roots of fractions:
- Separate the numerator and the denominator.
- Simplify the square root of each part.
- Rationalize the denominator if necessary.
- Combine the simplified parts if possible.
Simplifying Square Roots with Variables
When dealing with variables under a square root, follow these steps:
- Factor the expression under the square root, if possible.
- Identify any perfect squares within the factors.
- Take the square root of each perfect square outside the square root.
- If there are any remaining variables inside the square root, leave them as they are.
- Combine like terms outside the square root, if applicable.
Advanced Examples and Special Cases
Here are some advanced examples and special cases for simplifying square roots:
- Simplify \( \sqrt{75} \):
- Simplify \( \sqrt{200} \):
- Simplify \( \sqrt{18x^4} \):
- Simplify \( \sqrt{\frac{16}{25}} \):
- Simplify \( \sqrt{8 + 6\sqrt{2}} \):
\( \sqrt{75} = \sqrt{25 \times 3} = 5\sqrt{3} \), recognizing the perfect square factor.
\( \sqrt{200} = \sqrt{100 \times 2} = 10\sqrt{2} \), using a perfect square and simplifying.
\( \sqrt{18x^4} = \sqrt{9 \times 2 \times x^4} = 3x^2\sqrt{2} \), factoring and handling variables.
\( \sqrt{\frac{16}{25}} = \frac{\sqrt{16}}{\sqrt{25}} = \frac{4}{5} \), simplifying a square root of a fraction.
\( \sqrt{8 + 6\sqrt{2}} = \sqrt{2(4 + 3\sqrt{2})} = \sqrt{2}(\sqrt{4 + 3\sqrt{2}}) \), handling complex expressions.
Common Mistakes and How to Avoid Them
Here are common mistakes to avoid when simplifying square roots:
- Incorrectly applying square root rules.
- Forgetting to simplify perfect squares.
- Not rationalizing the denominator for square roots in fractions.
- Misidentifying factors inside the square root.
- Missing steps in the simplification process.

Practice Problems and Solutions
Below are several practice problems on simplifying square roots, followed by step-by-step solutions. Use these examples to test your understanding and improve your skills.
Problem 1
Simplify √72
Solution:
- Factor 72 into its prime factors: 72 = 2 × 2 × 2 × 3 × 3.
- Group the prime factors into pairs: (2 × 2) and (3 × 3).
- Take one factor from each pair outside the square root: 2 × 3 = 6.
- The simplified form of √72 is 6√2.
Problem 2
Simplify √180
Solution:
- Factor 180 into its prime factors: 180 = 2 × 2 × 3 × 3 × 5.
- Group the prime factors into pairs: (2 × 2) and (3 × 3).
- Take one factor from each pair outside the square root: 2 × 3 = 6.
- The simplified form of √180 is 6√5.
Problem 3
Simplify √50
Solution:
- Factor 50 into its prime factors: 50 = 2 × 5 × 5.
- Group the prime factors into pairs: (5 × 5).
- Take one factor from the pair outside the square root: 5.
- The simplified form of √50 is 5√2.
Problem 4
Simplify √128
Solution:
- Factor 128 into its prime factors: 128 = 2 × 2 × 2 × 2 × 2 × 2 × 2.
- Group the prime factors into pairs: (2 × 2), (2 × 2), and (2 × 2).
- Take one factor from each pair outside the square root: 2 × 2 × 2 = 8.
- The simplified form of √128 is 8√2.
Problem 5
Simplify √18 + √50
Solution:
- Simplify each square root separately:
- √18 = √(9 × 2) = 3√2
- √50 = √(25 × 2) = 5√2
- Combine like terms: 3√2 + 5√2 = (3 + 5)√2 = 8√2.
Problem 6
Simplify 2√20 + 4√5
Solution:
- Simplify each square root separately:
- 2√20 = 2√(4 × 5) = 2 × 2√5 = 4√5
- 4√5 remains the same.
- Combine like terms: 4√5 + 4√5 = (4 + 4)√5 = 8√5.
Problem 7
Simplify √(75/3)
Solution:
- First simplify the fraction under the square root: 75/3 = 25.
- Then take the square root of 25: √25 = 5.
- The simplified form of √(75/3) is 5.
Conclusion
Simplifying square roots is an essential skill in algebra that can be applied to various mathematical problems. By understanding the basic rules and techniques, such as prime factorization and the quotient property, you can simplify square roots with ease.
- Identify the prime factors of the number inside the square root.
- Pair the prime factors and move one factor out of the square root for each pair.
- Apply the quotient property for simplifying square roots of fractions.
- Practice with various examples to reinforce your understanding.
By mastering these techniques, you can confidently simplify square roots, making complex mathematical problems more manageable. Remember to practice regularly to enhance your skills and avoid common mistakes.
Understanding how to simplify square roots will not only help in solving algebraic equations but also in understanding more advanced mathematical concepts. Keep practicing, and you'll find that simplifying square roots becomes second nature.
Cách Đơn Giản Hóa Căn Bậc Hai
READ MORE:
Đơn Giản Hóa Căn Bậc Hai | Toán Học với Thầy J







