Topic simplify square root 18: Simplifying the square root of 18 can seem challenging, but with a clear, step-by-step approach, it becomes straightforward. This guide will walk you through the process, highlighting key techniques and tips. By the end, you'll be able to simplify √18 with confidence and understand its practical applications.
Table of Content
- Simplifying the Square Root of 18
- Introduction to Square Roots
- Basics of Simplifying Square Roots
- Step-by-Step Guide to Simplifying √18
- Factorization Method
- Identifying Perfect Squares
- Combining Simplified Results
- Examples and Practice Problems
- Common Mistakes to Avoid
- Practical Applications of Simplifying Square Roots
- Advanced Techniques in Simplifying Square Roots
- FAQs on Square Roots Simplification
- Conclusion and Further Resources
- YOUTUBE: Hướng dẫn đơn giản hóa căn bậc hai của 18 một cách dễ hiểu và chi tiết.
Simplifying the Square Root of 18
To simplify the square root of 18, follow these steps:
- Factorize 18
First, find the factors of 18. They are: 1, 2, 3, 6, 9, and 18.
- Identify Perfect Squares
From the list of factors, identify the perfect squares. Here, the perfect squares are 1 and 9.
- Divide by the Largest Perfect Square
Divide 18 by the largest perfect square identified, which is 9:
\( \frac{18}{9} = 2 \)
- Calculate the Square Root
Find the square root of the largest perfect square:
\( \sqrt{9} = 3 \)
- Combine the Results
Combine the results to get the simplest form of the square root of 18:
\( \sqrt{18} = 3\sqrt{2} \)
Why Simplify Square Roots?
Simplifying square roots makes expressions easier to work with, especially when adding, subtracting, or multiplying radicals. It reveals the underlying factors of the number, making calculations more straightforward and the results more understandable.
Additional Example
Let's see another example for more clarity:
Simplify \( \sqrt{12} \):
- Factors of 12: 1, 2, 3, 4, 6, 12
- Perfect squares: 1, 4
- Largest perfect square: 4
- Divide: \( \frac{12}{4} = 3 \)
- Square root of 4: \( \sqrt{4} = 2 \)
- Combine: \( \sqrt{12} = 2\sqrt{3} \)
Practical Applications
Simplifying square roots is useful in various fields such as engineering, physics, and computer science where precise calculations are essential. It is also crucial in solving quadratic equations and in trigonometry where simplifying expressions helps in finding exact values.
Now you have a clear understanding of how to simplify the square root of 18 and why it is important. Keep practicing with different numbers to master this skill!

READ MORE:
Introduction to Square Roots
Square roots are a fundamental concept in mathematics, representing a value that, when multiplied by itself, gives the original number. The symbol for the square root is √. Understanding square roots is essential for simplifying expressions, solving equations, and many practical applications in various fields such as engineering, physics, and computer science.
To simplify a square root, we aim to make the number inside the radical as small as possible while still remaining a whole number. This often involves factoring the number into its prime factors and identifying perfect squares.
For example, consider simplifying the square root of 18:
- Identify the factors of 18: 1, 2, 3, 6, 9, 18.
- Find the largest perfect square among the factors. Here, 9 is the largest perfect square.
- Rewrite 18 as the product of the perfect square and another factor: 18 = 9 × 2.
- Apply the square root to both factors: √18 = √(9 × 2) = √9 × √2.
- Calculate the square root of the perfect square: √9 = 3.
- Combine the results to get the simplified form: √18 = 3√2.
This step-by-step process helps in simplifying square roots efficiently, making calculations easier and more manageable.
Basics of Simplifying Square Roots
Simplifying square roots involves expressing a square root in its simplest radical form. This process makes the number inside the square root as small as possible while ensuring it remains a whole number. Here is a detailed step-by-step method to simplify square roots:
- Identify the prime factors of the number under the square root.
- Group the prime factors into pairs.
- Move one factor from each pair outside the square root.
- Multiply the factors outside the square root together.
- The remaining factor(s) inside the square root are multiplied together.
Let's simplify the square root of 18 as an example:
- Prime factorization of 18: \( 18 = 2 \times 3^2 \)
- Pair the prime factors: \( 3^2 \) can be taken out of the square root.
- Simplify: \( \sqrt{18} = \sqrt{2 \times 3^2} = 3\sqrt{2} \)
Therefore, the simplest form of \( \sqrt{18} \) is \( 3\sqrt{2} \).
Step-by-Step Guide to Simplifying √18
To simplify the square root of 18, follow these detailed steps:
-
List Factors:
First, list the factors of 18: 1, 2, 3, 6, 9, 18.
-
Identify Perfect Squares:
From the list of factors, identify the perfect squares. In this case, the perfect squares are 1 and 9.
-
Divide:
Divide 18 by the largest perfect square you found. Here, 18 ÷ 9 = 2.
-
Calculate the Square Root:
Calculate the square root of the largest perfect square. √9 = 3.
-
Combine Results:
Combine the results to get the simplified form of the square root of 18. Therefore, √18 = 3√2.
In summary, the simplified form of √18 is 3√2.
Factorization Method
The factorization method involves breaking down the number inside the square root into its prime factors. This method simplifies the process of finding the square root by focusing on identifying and using perfect square factors. Follow these steps to simplify √18 using the factorization method:
- Find the Prime Factors of 18:
Start by breaking down 18 into its prime factors. The prime factorization of 18 is:
18 = 2 × 3 × 3 = 2 × 32
- Rewrite the Square Root:
Next, rewrite the square root of 18 using the prime factors:
\(\sqrt{18} = \sqrt{2 \times 3^2}\)
- Separate the Perfect Squares:
Identify and separate the perfect square from the other factors inside the square root. In this case, \(3^2\) is a perfect square:
\(\sqrt{2 \times 3^2} = \sqrt{2} \times \sqrt{3^2}\)
- Simplify the Square Root of the Perfect Square:
Since the square root of \(3^2\) is 3, simplify the expression:
\(\sqrt{2} \times \sqrt{3^2} = \sqrt{2} \times 3\)
- Combine the Results:
Finally, multiply the simplified square root of the perfect square by the remaining square root:
\(\sqrt{18} = 3\sqrt{2}\)
Thus, the simplified form of \(\sqrt{18}\) is \(3\sqrt{2}\). Using the factorization method, you can simplify square roots by breaking down the number into its prime factors and then separating and simplifying the perfect squares.
Identifying Perfect Squares
Identifying perfect squares is an essential step in simplifying square roots. A perfect square is a number that is the square of an integer. Here are detailed steps to help you identify perfect squares when simplifying square roots:
- Understand What Perfect Squares Are:
A perfect square results from squaring an integer. For example:
- 1 is a perfect square (1 × 1)
- 4 is a perfect square (2 × 2)
- 9 is a perfect square (3 × 3)
- 16 is a perfect square (4 × 4)
- 25 is a perfect square (5 × 5)
- Identify Perfect Squares in Factorization:
When simplifying a square root, factorize the number and look for pairs of identical factors. These pairs represent perfect squares. For example, consider the number 18:
18 = 2 × 3 × 3 = 2 × 32
- Separate Perfect Squares from Other Factors:
Rewrite the expression to separate the perfect squares from other factors:
\(\sqrt{18} = \sqrt{2 \times 3^2} = \sqrt{2} \times \sqrt{3^2}\)
- Simplify the Square Root of Perfect Squares:
Since \(\sqrt{3^2} = 3\), the expression can be simplified to:
\(\sqrt{18} = \sqrt{2} \times 3 = 3\sqrt{2}\)
By identifying and using perfect squares, the process of simplifying square roots becomes much easier. Always look for factors that are perfect squares and separate them from the other factors to simplify the expression effectively.
Combining Simplified Results
Combining simplified results involves using properties of square roots to simplify expressions into their simplest form. Here is a detailed step-by-step method:
- Express Each Square Root in Simplified Form
- For example, simplify
\(\sqrt{18}\) . - As shown earlier,
\(\sqrt{18} = 3\sqrt{2}\) .
- For example, simplify
- Combine Like Terms
- If you have multiple terms involving the same square root, combine them by adding or subtracting the coefficients.
- For instance, simplify
\(2\sqrt{18} + 3\sqrt{2}\) . - First, write
\(2\sqrt{18} \) as\(2 \cdot 3\sqrt{2} = 6\sqrt{2}\) . - Now, combine the terms:
\(6\sqrt{2} + 3\sqrt{2} = 9\sqrt{2}\) .
- Multiplying and Dividing Square Roots
- When multiplying or dividing square roots, use the property
\(\sqrt{a} \cdot \sqrt{b} = \sqrt{ab}\) and\(\frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}}\) . - For example,
\(\sqrt{2} \cdot \sqrt{8} = \sqrt{2 \cdot 8} = \sqrt{16} = 4\) . - Another example,
\(\frac{\sqrt{18}}{\sqrt{2}} = \sqrt{\frac{18}{2}} = \sqrt{9} = 3\) .
- When multiplying or dividing square roots, use the property
- Complex Expressions
- For expressions involving multiple square roots, break them into simpler parts.
- For example,
\(2\sqrt{12} + 3\sqrt{27}\) can be simplified as: \(2 \cdot 2\sqrt{3} + 3 \cdot 3\sqrt{3} = 4\sqrt{3} + 9\sqrt{3} = 13\sqrt{3}\) .
By following these steps, you can effectively combine and simplify square root expressions, making them easier to work with in various mathematical contexts.
Examples and Practice Problems
Understanding the process of simplifying square roots can be reinforced through practice. Here are several examples and practice problems to help you master this skill.
Example 1: Simplifying √18
To simplify √18, we follow these steps:
- Factor 18 into its prime factors: 18 = 2 × 3 × 3.
- Pair the prime factors: (3 × 3) × 2.
- Take the square root of the paired factor: √(3 × 3) = 3.
- Multiply the result outside the square root by the remaining factor inside the square root: 3√2.
Thus, √18 simplifies to 3√2.
Example 2: Simplifying √50
To simplify √50, follow these steps:
- Factor 50 into its prime factors: 50 = 2 × 5 × 5.
- Pair the prime factors: (5 × 5) × 2.
- Take the square root of the paired factor: √(5 × 5) = 5.
- Multiply the result outside the square root by the remaining factor inside the square root: 5√2.
Thus, √50 simplifies to 5√2.
Example 3: Simplifying √72
To simplify √72, follow these steps:
- Factor 72 into its prime factors: 72 = 2 × 2 × 2 × 3 × 3.
- Pair the prime factors: (2 × 2) × (3 × 3) × 2.
- Take the square root of each paired factor: √(2 × 2) = 2 and √(3 × 3) = 3.
- Multiply the results outside the square root and leave the remaining factor inside: 2 × 3√2 = 6√2.
Thus, √72 simplifies to 6√2.
Practice Problems
Try simplifying the following square roots on your own. Check your answers below to see if you got them correct.
- Simplify √45
- Simplify √27
- Simplify √98
- Simplify √200
Solutions to Practice Problems
- √45 = 3√5
- √27 = 3√3
- √98 = 7√2
- √200 = 10√2
By practicing these problems, you can strengthen your understanding and ability to simplify square roots effectively.
Common Mistakes to Avoid
Simplifying square roots can sometimes lead to mistakes. Here are some common errors and how to avoid them:
- Forgetting to check for perfect squares: Always identify and use the largest perfect square factor of the number under the square root. For example, with √18, recognize that 9 (a perfect square) is a factor.
- Rushing through the steps: Simplification requires careful, step-by-step calculations. Ensure you factorize correctly and combine terms properly. Take your time to avoid errors.
- Incorrect factorization: Ensure you break down the number into its prime factors accurately. For instance, 18 should be factorized into 2 × 3², not 2 × 9.
- Overlooking the prime factors: Simplify the expression by correctly pairing prime factors. For √18, factorize it as 3√2 by taking out the square of 3.
- Misplacing decimal points: When converting to decimal form, ensure accuracy in placement and calculation. Simplifying √18 to its decimal form should yield approximately 4.24264.
- Not verifying the result: Always check your final simplified form by squaring it back to ensure it matches the original number. For example, (3√2)² should equal 18.
By being aware of these common mistakes, you can improve your skills in simplifying square roots and ensure your results are accurate and simplified correctly.
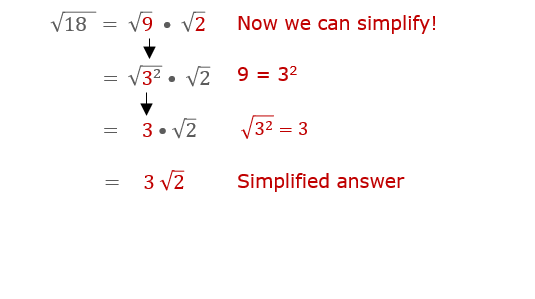
Practical Applications of Simplifying Square Roots
Simplifying square roots is not just an academic exercise; it has numerous practical applications across various fields. Here are some key areas where simplified square roots are particularly useful:
1. Geometry and Trigonometry
In geometry, simplifying square roots is essential for calculating distances, areas, and volumes. For instance:
- Distance Formula: The distance between two points \((x_1, y_1)\) and \((x_2, y_2)\) in a coordinate plane is given by \(d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\). Simplifying the square root can make calculations easier.
- Pythagorean Theorem: In a right triangle, the length of the hypotenuse \(c\) is given by \(c = \sqrt{a^2 + b^2}\), where \(a\) and \(b\) are the lengths of the other two sides. Simplifying this expression helps in finding exact side lengths.
2. Engineering and Physics
Square roots appear frequently in engineering and physics formulas:
- Wave Equations: The speed of a wave \(v\) in a medium can be given by \(v = \sqrt{\frac{T}{\mu}}\), where \(T\) is the tension in the medium and \(\mu\) is the mass per unit length. Simplifying helps in practical calculations.
- Electric Circuits: In alternating current (AC) circuits, the impedance \(Z\) is calculated as \(Z = \sqrt{R^2 + (XL - XC)^2}\), where \(R\) is resistance, \(XL\) is inductive reactance, and \(XC\) is capacitive reactance.
3. Finance
In finance, square roots are used in various models and formulas:
- Standard Deviation: In statistics, the standard deviation is calculated as the square root of the variance. Simplifying the square root can make interpreting the standard deviation easier.
- Interest Rate Calculations: The effective annual rate (EAR) can involve square roots, particularly in compound interest formulas.
4. Computer Graphics
Simplifying square roots is crucial in computer graphics for rendering images and animations:
- Distance and Lighting Calculations: In 3D graphics, the distance between objects and light sources often requires square root calculations for realistic rendering.
- Vector Normalization: Normalizing vectors in graphics involves dividing a vector by its magnitude, which includes a square root calculation.
5. Everyday Life
Square roots are also encountered in daily life situations:
- Construction: Calculating diagonal distances in construction projects often requires simplifying square roots, such as finding the length of a diagonal brace in a rectangular frame.
- Cooking: Recipes may sometimes require adjustments involving square roots, such as scaling ingredient amounts for different sized batches.
Understanding how to simplify square roots enhances your ability to solve problems efficiently in these areas and more, demonstrating the practical importance of this mathematical skill.
Advanced Techniques in Simplifying Square Roots
While basic methods for simplifying square roots are often sufficient, there are several advanced techniques that can be useful for more complex expressions. These methods include rationalizing the denominator, using prime factorization, and simplifying expressions with variables. Here, we will explore these techniques step-by-step.
1. Rationalizing the Denominator
When a square root appears in the denominator of a fraction, it is often helpful to rationalize the denominator. This process involves removing the square root from the denominator by multiplying both the numerator and the denominator by a suitable value.
- Identify the square root in the denominator.
- Multiply both the numerator and the denominator by the same square root to eliminate the root in the denominator.
For example, to simplify \( \frac{1}{\sqrt{2}} \):
\[ \frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2} \]
2. Using Prime Factorization
Prime factorization involves breaking down a number into its prime factors, which can then be used to simplify the square root.
- Factor the number under the square root into its prime factors.
- Group the prime factors into pairs.
- Take one factor from each pair out of the square root.
For example, to simplify \( \sqrt{72} \):
\[ 72 = 2 \times 2 \times 2 \times 3 \times 3 \]
\[ \sqrt{72} = \sqrt{(2 \times 2) \times (3 \times 3) \times 2} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2} \]
3. Simplifying Expressions with Variables
Square roots of expressions involving variables can also be simplified using similar techniques.
- Factor the expression inside the square root.
- Apply the square root to each factor separately.
- Simplify the expression by taking out pairs of variables.
For example, to simplify \( \sqrt{50x^4y^2} \):
\[ 50x^4y^2 = 2 \times 5^2 \times (x^2)^2 \times y^2 \]
\[ \sqrt{50x^4y^2} = \sqrt{2} \times 5 \times x^2 \times y = 5x^2y\sqrt{2} \]
4. Simplifying Complex Fractions
For fractions involving square roots, simplify each part individually before combining them.
- Simplify the numerator and denominator separately.
- Combine the simplified results.
For example, to simplify \( \sqrt{\frac{8x^3}{2x}} \):
\[ \sqrt{\frac{8x^3}{2x}} = \sqrt{4x^2} = 2x \]
Practice Problems
Try simplifying the following expressions using these advanced techniques:
- \( \sqrt{50} \)
- \( \frac{3}{\sqrt{5}} \)
- \( \sqrt{72x^2} \)
- \( \sqrt{\frac{32x^3}{4x}} \)
By mastering these advanced techniques, you can simplify even the most complex square root expressions with ease!
FAQs on Square Roots Simplification
-
What is the square root of -18?
The square root of a negative number is an imaginary number. Therefore, the square root of -18 is represented as \( \sqrt{-18} = 3\sqrt{2}i \).
-
Can we find the square root of 18 by the repeated subtraction method?
No, the repeated subtraction method can only be used for perfect squares, and since 18 is not a perfect square, this method is not applicable.
-
What is the prime factorization of 18?
The prime factorization of 18 is \( 2 \times 3^2 \). This can be useful in simplifying the square root of 18 to \( 3\sqrt{2} \).
-
Is the square root of 18 a rational number?
No, the square root of 18 is not a rational number. It is an irrational number because its decimal representation is non-terminating and non-repeating.
-
Is -3√2 also a square root of 18?
Yes, both \( 3\sqrt{2} \) and \( -3\sqrt{2} \) are square roots of 18, since squaring either of these values results in 18.
Conclusion and Further Resources
Simplifying square roots, such as \(\sqrt{18}\), is a valuable skill in various fields of mathematics and practical applications. By breaking down complex square roots into their simplest forms, you make calculations more manageable and results more comprehensible.
To recap, here are the main steps for simplifying square roots:
- Identify the factors of the number under the square root, looking for perfect squares.
- Express the number as a product of these factors.
- Simplify the square root of the perfect square and combine it with the remaining factor.
For example, simplifying \(\sqrt{18}\) involves recognizing that \(18 = 9 \times 2\). Since \(9\) is a perfect square, we can simplify this to \(3\sqrt{2}\).
Further Resources
To deepen your understanding and practice simplifying square roots, here are some helpful resources:
- - Comprehensive video lessons and practice problems.
- - Clear explanations and examples.
- - Tool for simplifying square roots and other mathematical expressions.
By leveraging these resources and practicing regularly, you can become proficient in simplifying square roots and applying this knowledge in various mathematical contexts.
Hướng dẫn đơn giản hóa căn bậc hai của 18 một cách dễ hiểu và chi tiết.
Cách Đơn Giản Hóa Căn Bậc Hai của 18: Sqrt(18)
READ MORE:
Hướng dẫn cách tìm và đơn giản hóa căn bậc hai của số 18 một cách chi tiết.
Căn Bậc Hai của 18










