Topic simplify square root of 54: Unlock the secret to simplifying the square root of 54 with our easy-to-follow guide! Whether you're a student or math enthusiast, learn the prime factorization technique and master the simplification of √54 to its simplest form. Transform complex problems into manageable solutions with practical examples and step-by-step instructions.
Table of Content
- How to Simplify the Square Root of 54
- Introduction to Simplifying Square Roots
- Prime Factorization Method
- Step-by-Step Simplification of √54
- Visualizing the Simplification Process
- Common Mistakes and How to Avoid Them
- Applications of Simplified Square Roots
- Practice Problems and Solutions
- Frequently Asked Questions (FAQs)
- Conclusion and Summary
- YOUTUBE: Video hướng dẫn cách đơn giản hóa căn bậc hai của 54: Sqrt(54).
How to Simplify the Square Root of 54
Simplifying square roots involves breaking down the number inside the square root into its prime factors and then simplifying. Here, we'll show you how to simplify the square root of 54 step by step.
Step-by-Step Solution
- Find the Prime Factors: Start by finding the prime factors of 54. We see that 54 can be factored into 2 and 27, and 27 can be further factored into 3 and 9, and 9 into 3 and 3. So, the prime factors of 54 are:
- 54 = 2 × 3 × 3 × 3
- Group the Factors: To simplify, group the prime factors into pairs where possible:
- 54 = 2 × (3 × 3) × 3
- Simplify: Take the square root of each group:
- \(\sqrt{54} = \sqrt{2 \times (3^2) \times 3}\)
- \(\sqrt{54} = \sqrt{2} \times 3 \times \sqrt{3}\)
- \(\sqrt{54} = 3\sqrt{6}\)
Result
Therefore, the simplified form of the square root of 54 is:
Visualization
Visualizing the simplification can be helpful. Below is a diagram showing the process:
| Original Expression | Prime Factorization | Grouping | Simplified Form |
| \(\sqrt{54}\) | \(\sqrt{2 \times 3 \times 3 \times 3}\) | \(\sqrt{2 \times (3^2) \times 3}\) | \(3\sqrt{6}\) |

READ MORE:
Introduction to Simplifying Square Roots
Simplifying square roots is a fundamental skill in mathematics that makes complex expressions easier to handle. When we simplify the square root of a number, we express it in its simplest radical form. This process involves breaking down the number inside the square root into its prime factors and simplifying where possible. Here's how to simplify square roots step by step:
- Understand the Concept: The goal is to express the square root in the form of \(a\sqrt{b}\), where \(a\) and \(b\) are integers, and \(b\) has no perfect square factors other than 1.
- Find Prime Factors: Identify the prime factors of the number under the square root. For example, for 54, the prime factors are 2 and 3:
- 54 = 2 × 3 × 3 × 3
- Group the Factors: Arrange the prime factors into pairs. Pairing helps to extract a perfect square from under the square root:
- \(\sqrt{54} = \sqrt{2 \times 3 \times 3 \times 3} = \sqrt{2 \times (3^2) \times 3}\)
- Simplify: Simplify by taking the square root of the paired factors and moving them outside the square root sign:
- \(\sqrt{54} = \sqrt{2 \times (3^2) \times 3} = 3\sqrt{6}\)
In essence, simplifying square roots involves finding the largest perfect square factor of the number and then simplifying it to make calculations more manageable. Practice with different numbers to get a strong grasp of this valuable mathematical technique!
| Number | Prime Factorization | Simplified Form |
|---|---|---|
| 54 | 2 × 3 × 3 × 3 | 3\(\sqrt{6}\) |
| 72 | 2 × 2 × 2 × 3 × 3 | 6\(\sqrt{2}\) |
| 98 | 2 × 7 × 7 | 7\(\sqrt{2}\) |
Prime Factorization Method
The Prime Factorization Method is a systematic way to simplify square roots by breaking down the number inside the square root into its prime factors. This method makes it easier to extract perfect squares and simplify the expression. Let’s walk through the process of simplifying the square root of 54 using prime factorization.
- Find the Prime Factors: Determine the prime factors of the number inside the square root. Prime factors are the prime numbers that multiply together to give the original number.
- For 54, start by dividing by the smallest prime number, 2:
- 54 ÷ 2 = 27
- Next, divide 27 by the next smallest prime number, 3:
- 27 ÷ 3 = 9
- Continue dividing by 3:
- 9 ÷ 3 = 3
- Finally, 3 is a prime number itself. The prime factors of 54 are 2 and 3:
- 54 = 2 × 3 × 3 × 3
- For 54, start by dividing by the smallest prime number, 2:
- Group the Prime Factors: Organize the prime factors into pairs where possible to identify perfect squares:
- \(\sqrt{54} = \sqrt{2 \times 3 \times 3 \times 3}\)
- Group the 3s: \(\sqrt{54} = \sqrt{2 \times (3^2) \times 3}\)
- Extract Perfect Squares: Move the square root of the paired factors outside the radical. Since \(3^2\) is a perfect square, it can be simplified:
- \(\sqrt{54} = \sqrt{2} \times 3 \times \sqrt{3}\)
- Simplify further: \(\sqrt{54} = 3\sqrt{6}\)
By using the Prime Factorization Method, we have simplified the square root of 54 to \(3\sqrt{6}\). This method is reliable and can be applied to any number to simplify square roots effectively.
| Number | Prime Factorization | Grouping | Simplified Form |
|---|---|---|---|
| 54 | 2 × 3 × 3 × 3 | \(\sqrt{2 \times (3^2) \times 3}\) | 3\(\sqrt{6}\) |
| 75 | 3 × 5 × 5 | \(\sqrt{3 \times (5^2)}\) | 5\(\sqrt{3}\) |
| 45 | 3 × 3 × 5 | \(\sqrt{(3^2) \times 5}\) | 3\(\sqrt{5}\) |
Step-by-Step Simplification of √54
Simplifying the square root of 54 involves breaking down the number into its prime factors and extracting the perfect squares. Here’s a detailed step-by-step guide to simplify \(\sqrt{54}\) to its simplest form.
- Prime Factorization: Identify the prime factors of 54.
- 54 can be divided by 2, the smallest prime number:
- 54 ÷ 2 = 27
- Next, divide 27 by 3, the next smallest prime number:
- 27 ÷ 3 = 9
- Continue dividing 9 by 3:
- 9 ÷ 3 = 3
- Finally, 3 is a prime number itself. So, the prime factorization of 54 is:
- 54 = 2 × 3 × 3 × 3
- 54 can be divided by 2, the smallest prime number:
- Organize and Group the Factors: Group the prime factors into pairs to identify perfect squares.
- Rearrange the factors: \(54 = 2 \times 3 \times 3 \times 3\)
- Group the 3s: \(54 = 2 \times (3^2) \times 3\)
- Simplify the Square Root: Take the square root of the grouped factors.
- Express the square root with the grouped factors: \(\sqrt{54} = \sqrt{2 \times (3^2) \times 3}\)
- Extract the perfect square from the square root:
- \(\sqrt{54} = \sqrt{2} \times \sqrt{3^2} \times \sqrt{3}\)
- Simplify the expression: \(\sqrt{54} = \sqrt{2} \times 3 \times \sqrt{3}\)
- Combine the terms: \(\sqrt{54} = 3\sqrt{6}\)
The square root of 54 has been simplified to \(3\sqrt{6}\). This step-by-step process can be applied to other numbers to simplify their square roots effectively.
| Number | Prime Factors | Grouped Factors | Simplified Form |
|---|---|---|---|
| 54 | 2 × 3 × 3 × 3 | 2 × (3²) × 3 | 3\(\sqrt{6}\) |
| 75 | 3 × 5 × 5 | 3 × (5²) | 5\(\sqrt{3}\) |
| 200 | 2 × 2 × 2 × 5 × 5 | (2²) × 2 × (5²) | 10\(\sqrt{2}\) |
Visualizing the Simplification Process
To visualize the process of simplifying the square root of 54, we can use the prime factorization method. This method involves breaking down the number into its prime factors and then simplifying the square root step-by-step. Let's go through the process in detail:
-
Prime Factorization of 54:
The first step is to find the prime factors of 54.
- 54 is an even number, so it is divisible by 2: \(54 \div 2 = 27\).
- Next, 27 is divisible by 3: \(27 \div 3 = 9\).
- Finally, 9 is also divisible by 3: \(9 \div 3 = 3\).
- Thus, the prime factorization of 54 is: \(2 \times 3 \times 3 \times 3\) or \(2 \times 3^3\).
-
Group the Prime Factors:
To simplify the square root, we group the prime factors into pairs.
- We have one 2 and three 3s: \(2 \times 3^3\).
- We can pair two of the 3s: \(3 \times 3 = 9\).
-
Simplify the Square Root:
Now, we can take the square root of each pair and multiply the results.
- \(\sqrt{54} = \sqrt{2 \times 3^3}\).
- \(\sqrt{2 \times 3 \times 3 \times 3} = \sqrt{2} \times \sqrt{3 \times 3 \times 3}\).
- \(\sqrt{3 \times 3} = 3\), so we get: \(\sqrt{54} = 3 \times \sqrt{6}\).
- Thus, the simplified form is \(\sqrt{54} = 3\sqrt{6}\).
The following table summarizes the steps for simplifying the square root of 54:
| Step | Description | Result |
|---|---|---|
| Prime Factorization | Factor 54 into prime numbers | 2, 3, 3, 3 |
| Group Factors | Group the prime factors into pairs | \(2 \times 3^3\) |
| Simplify | Take the square root of each pair and multiply the results | \(3\sqrt{6}\) |
By following these steps, you can easily visualize and understand the simplification process of the square root of 54.
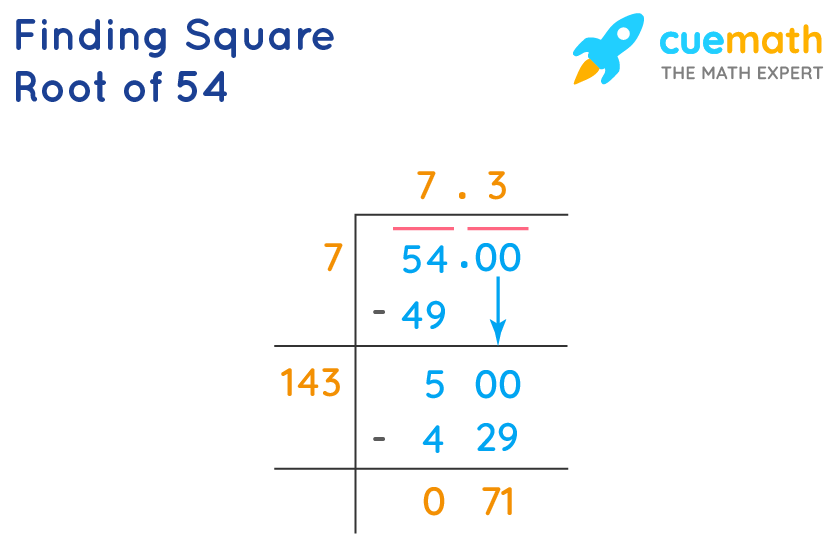
Common Mistakes and How to Avoid Them
When simplifying the square root of 54, there are several common mistakes that students often make. By being aware of these mistakes, you can avoid them and simplify square roots correctly. Here are some common errors and how to prevent them:
-
Incorrect Prime Factorization:
One common mistake is not correctly finding the prime factors of 54. This can lead to incorrect simplification.
- Mistake: Misidentifying the prime factors, such as thinking \(54 = 2 \times 27\) without further breaking down 27.
- Solution: Ensure that you factorize each composite number completely until all factors are prime numbers. For 54, the correct factorization is \(54 = 2 \times 3 \times 3 \times 3\) or \(2 \times 3^3\).
-
Incorrect Grouping of Factors:
Another mistake is not properly grouping the prime factors into pairs.
- Mistake: Grouping incorrectly, such as pairing one 3 with the 2, which leads to wrong simplification steps.
- Solution: Carefully group the prime factors. For 54, pair the 3s together: \(2 \times 3^3\) gives us a pair of 3s (3 × 3) and one remaining 3. This helps in correct simplification.
-
Incorrect Simplification of Square Roots:
Students often make mistakes in simplifying the square roots after factorization.
- Mistake: Simplifying the square root without recognizing perfect squares within the factors, such as missing that \(3 \times 3 = 9\) is a perfect square.
- Solution: Recognize and simplify perfect squares. In \(\sqrt{54} = \sqrt{2 \times 3^3}\), identify \(\sqrt{3 \times 3} = 3\) and simplify: \(\sqrt{54} = 3\sqrt{6}\).
-
Forgetting to Simplify Completely:
Sometimes, students stop simplifying too early and do not simplify completely.
- Mistake: Leaving the expression partly simplified, such as \(\sqrt{54} = \sqrt{2 \times 27}\) without breaking down 27 further.
- Solution: Continue simplifying until you cannot simplify further. For \(\sqrt{54}\), ensure you simplify to \(\sqrt{2 \times 3 \times 3 \times 3}\) which ultimately simplifies to \(3\sqrt{6}\).
-
Misunderstanding Square Root Properties:
A fundamental error is misunderstanding the properties of square roots and multiplication.
- Mistake: Misapplying properties, such as thinking \(\sqrt{ab} = \sqrt{a} + \sqrt{b}\) instead of \(\sqrt{ab} = \sqrt{a} \times \sqrt{b}\).
- Solution: Always apply the correct properties: \(\sqrt{ab} = \sqrt{a} \times \sqrt{b}\). For \(\sqrt{54}\), apply it correctly to get \(\sqrt{2 \times 27} = \sqrt{2} \times \sqrt{27}\).
By understanding and avoiding these common mistakes, you can accurately and confidently simplify square roots like \(\sqrt{54}\) to their simplest form.
Applications of Simplified Square Roots
Simplified square roots are not just a mathematical exercise; they have practical applications in various fields. Here are some key applications of simplified square roots:
-
Geometry and Trigonometry:
Simplified square roots are frequently used in geometry and trigonometry, especially when dealing with right triangles, circles, and other geometric shapes.
- Example: In a right triangle, the length of the hypotenuse can be found using the Pythagorean theorem: \(c = \sqrt{a^2 + b^2}\). If \(a = 6\) and \(b = 3\sqrt{6}\), then \(c = \sqrt{6^2 + (3\sqrt{6})^2} = \sqrt{36 + 54} = \sqrt{90} = 3\sqrt{10}\).
-
Physics and Engineering:
In physics and engineering, square roots appear in formulas involving waves, oscillations, and areas under curves.
- Example: The formula for the period of a pendulum is \(T = 2\pi\sqrt{\frac{L}{g}}\), where \(L\) is the length of the pendulum and \(g\) is the acceleration due to gravity. Simplifying square roots helps in calculating the period more efficiently.
-
Statistics:
In statistics, the standard deviation involves the square root function. Simplified square roots help in understanding and interpreting statistical data.
- Example: If the variance of a dataset is 54, the standard deviation is \(\sqrt{54} = 3\sqrt{6}\).
-
Computer Science:
Algorithms in computer science, especially those related to graphics and spatial calculations, often use square roots.
- Example: Calculating the distance between two points in a 2D plane uses the distance formula: \(d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\). Simplifying square roots helps optimize these calculations for faster processing.
-
Everyday Life:
Simplified square roots can also be applied in daily activities, such as determining the size of a TV or monitor screen, or figuring out the area of a space.
- Example: If you have a square garden with an area of 54 square meters, the length of each side is \(\sqrt{54} = 3\sqrt{6}\) meters.
Understanding how to simplify square roots can thus be beneficial in various practical situations, making it a valuable skill to master.
Practice Problems and Solutions
Practicing the simplification of square roots is essential to master the process. Here are some practice problems along with detailed solutions to help you understand the steps involved:
-
Problem 1: Simplify \(\sqrt{54}\).
Solution:
- Prime factorize 54: \(54 = 2 \times 3^3\).
- Group the factors: \(2 \times 3 \times 3 \times 3\).
- Simplify the square root: \(\sqrt{54} = \sqrt{2 \times 3 \times 3 \times 3} = 3\sqrt{6}\).
-
Problem 2: Simplify \(\sqrt{72}\).
Solution:
- Prime factorize 72: \(72 = 2^3 \times 3^2\).
- Group the factors: \(2 \times 2 \times 2 \times 3 \times 3\).
- Simplify the square root: \(\sqrt{72} = \sqrt{2^3 \times 3^2} = \sqrt{2 \times 2 \times 2 \times 3 \times 3} = 6\sqrt{2}\).
-
Problem 3: Simplify \(\sqrt{98}\).
Solution:
- Prime factorize 98: \(98 = 2 \times 7^2\).
- Group the factors: \(2 \times 7 \times 7\).
- Simplify the square root: \(\sqrt{98} = \sqrt{2 \times 7^2} = \sqrt{2 \times 7 \times 7} = 7\sqrt{2}\).
-
Problem 4: Simplify \(\sqrt{200}\).
Solution:
- Prime factorize 200: \(200 = 2^3 \times 5^2\).
- Group the factors: \(2 \times 2 \times 2 \times 5 \times 5\).
- Simplify the square root: \(\sqrt{200} = \sqrt{2^3 \times 5^2} = \sqrt{2 \times 2 \times 2 \times 5 \times 5} = 10\sqrt{2}\).
-
Problem 5: Simplify \(\sqrt{245}\).
Solution:
- Prime factorize 245: \(245 = 5 \times 7^2\).
- Group the factors: \(5 \times 7 \times 7\).
- Simplify the square root: \(\sqrt{245} = \sqrt{5 \times 7^2} = \sqrt{5 \times 7 \times 7} = 7\sqrt{5}\).
These practice problems demonstrate the step-by-step process of simplifying square roots using prime factorization. By working through these examples, you can gain a better understanding and become more proficient in simplifying square roots.
Frequently Asked Questions (FAQs)
Here are some frequently asked questions about simplifying square roots, specifically focusing on the square root of 54:
-
What is the simplified form of \(\sqrt{54}\)?
The simplified form of \(\sqrt{54}\) is \(3\sqrt{6}\). This is found by breaking down 54 into its prime factors and simplifying:
- Prime factorize 54: \(54 = 2 \times 3^3\).
- Group the factors: \(2 \times 3 \times 3 \times 3\).
- Simplify: \(\sqrt{54} = 3\sqrt{6}\).
-
Why do we need to simplify square roots?
Simplifying square roots makes them easier to work with in equations and other mathematical problems. It also provides a more exact form of the square root, which can be useful in various applications like geometry, physics, and engineering.
-
How do you simplify a square root using prime factorization?
To simplify a square root using prime factorization, follow these steps:
- Factor the number into its prime factors.
- Group the prime factors into pairs.
- Take the square root of each pair and multiply the results.
- Multiply any remaining factors inside the square root.
For example, to simplify \(\sqrt{54}\):
- Prime factorize 54: \(54 = 2 \times 3^3\).
- Group the factors: \(2 \times 3 \times 3 \times 3\).
- Simplify: \(\sqrt{54} = 3\sqrt{6}\).
-
Can all square roots be simplified?
No, not all square roots can be simplified. Only square roots of numbers that have square factors can be simplified. For example, \(\sqrt{18}\) can be simplified to \(3\sqrt{2}\) because 18 has the square factor 9. However, \(\sqrt{7}\) cannot be simplified further because 7 is a prime number and does not have any square factors.
-
Is \(\sqrt{54}\) a rational number?
No, \(\sqrt{54}\) is not a rational number. A rational number can be expressed as a fraction of two integers. Since \(\sqrt{54}\) simplifies to \(3\sqrt{6}\) and \(\sqrt{6}\) is an irrational number, \(\sqrt{54}\) is also irrational.
Understanding these frequently asked questions can help clarify the process and importance of simplifying square roots.

Conclusion and Summary
In this article, we explored the process of simplifying the square root of 54 and its broader applications. By understanding and mastering this process, you can enhance your mathematical skills and apply them in various fields. Here is a summary of the key points covered:
-
Introduction to Simplifying Square Roots: We began by understanding the importance of simplifying square roots and the general approach to doing so.
-
Prime Factorization Method: We used the prime factorization method to break down 54 into its prime factors: \(2 \times 3^3\).
-
Step-by-Step Simplification of \(\sqrt{54}\): By grouping the factors and simplifying, we found that \(\sqrt{54} = 3\sqrt{6}\).
-
Visualizing the Simplification Process: We visualized the simplification process through detailed steps and examples.
-
Common Mistakes and How to Avoid Them: We highlighted common mistakes such as incorrect prime factorization and improper grouping of factors, and provided tips to avoid them.
-
Applications of Simplified Square Roots: Simplified square roots have practical applications in geometry, physics, engineering, statistics, computer science, and everyday life.
-
Practice Problems and Solutions: We provided practice problems with solutions to reinforce the learning process and ensure proficiency.
-
Frequently Asked Questions (FAQs): We answered common questions related to simplifying square roots, providing clarity and further understanding.
By mastering the simplification of square roots, including the square root of 54, you gain valuable skills that are applicable in many mathematical and real-world contexts. Continue practicing and applying these concepts to become more confident and proficient in your mathematical journey.
Video hướng dẫn cách đơn giản hóa căn bậc hai của 54: Sqrt(54).
Cách Đơn Giản Hóa Căn Bậc Hai của 54: Sqrt(54)
READ MORE:
Video hướng dẫn cách đơn giản hóa căn bậc hai của 54.
Đơn Giản Hóa Căn Bậc Hai của 54








