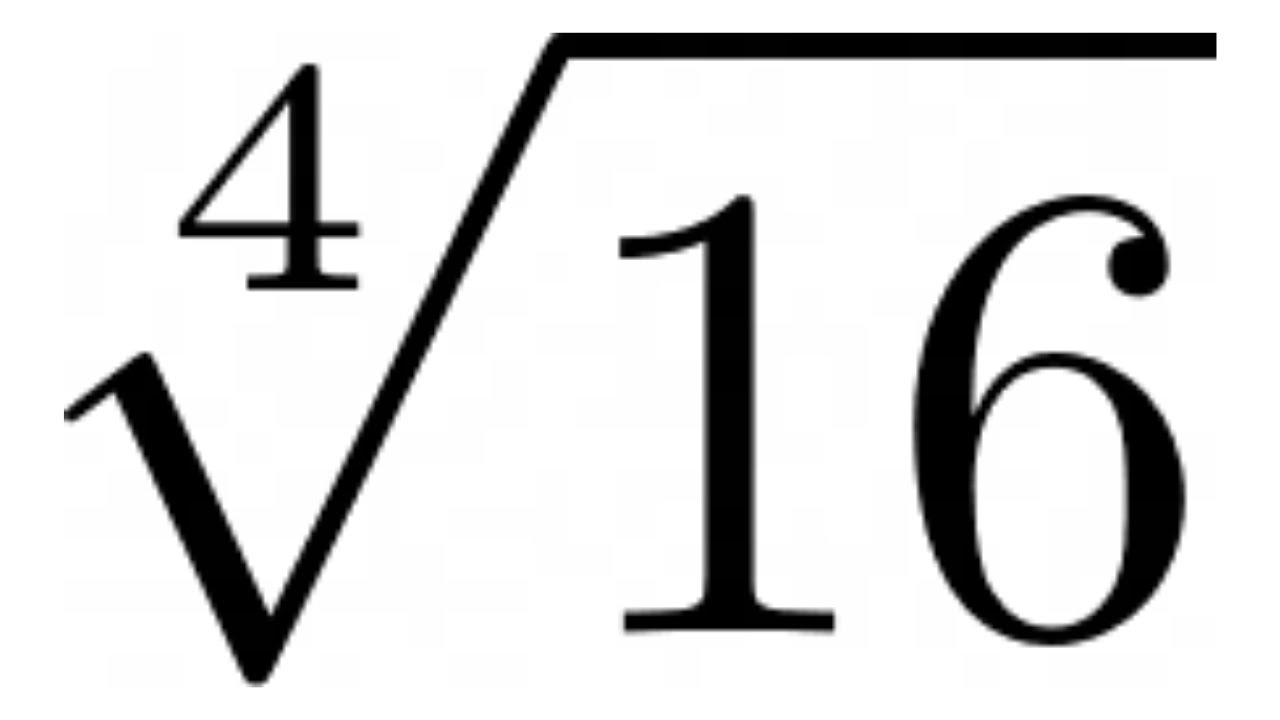Topic simplify square root of 16: Discover how to simplify the square root of 16 easily and efficiently. This comprehensive guide breaks down the steps to simplify √16, explains the mathematical principles behind it, and explores practical applications. Perfect for students, educators, and anyone looking to strengthen their math skills.
Table of Content
- Simplify the Square Root of 16
- Introduction to Square Roots
- Understanding Perfect Squares
- Step-by-Step Guide to Simplifying √16
- Mathematical Explanation and Verification
- Applications of Simplifying Square Roots
- Common Mistakes and How to Avoid Them
- Advanced Concepts Related to Square Roots
- Practice Problems and Solutions
- Additional Resources and Tools
- Conclusion
- YOUTUBE: Hướng dẫn cách đơn giản hóa căn bậc hai của 16: sqrt(16). Video này sẽ giúp bạn hiểu rõ hơn về cách tính toán và ứng dụng của căn bậc hai trong toán học.
Simplify the Square Root of 16
To simplify the square root of 16, follow these steps:
Step-by-Step Process
- Identify the number under the square root: \( \sqrt{16} \)
- Determine if the number is a perfect square. A perfect square is an integer that is the square of another integer. In this case, 16 is a perfect square because \( 4^2 = 16 \).
- Simplify the square root by finding the square root of the perfect square. Thus, \( \sqrt{16} = 4 \).
The simplified form of \( \sqrt{16} \) is 4.
Mathematical Representation
Using Mathjax, we can represent this as:
\[ \sqrt{16} = 4 \]
Verification
To verify, we can square the result:
\[ 4^2 = 16 \]
Since 16 is equal to the original number under the square root, the simplification is correct.
Applications
Knowing how to simplify square roots is useful in various mathematical contexts, such as solving quadratic equations, simplifying expressions, and performing calculations in geometry and algebra.
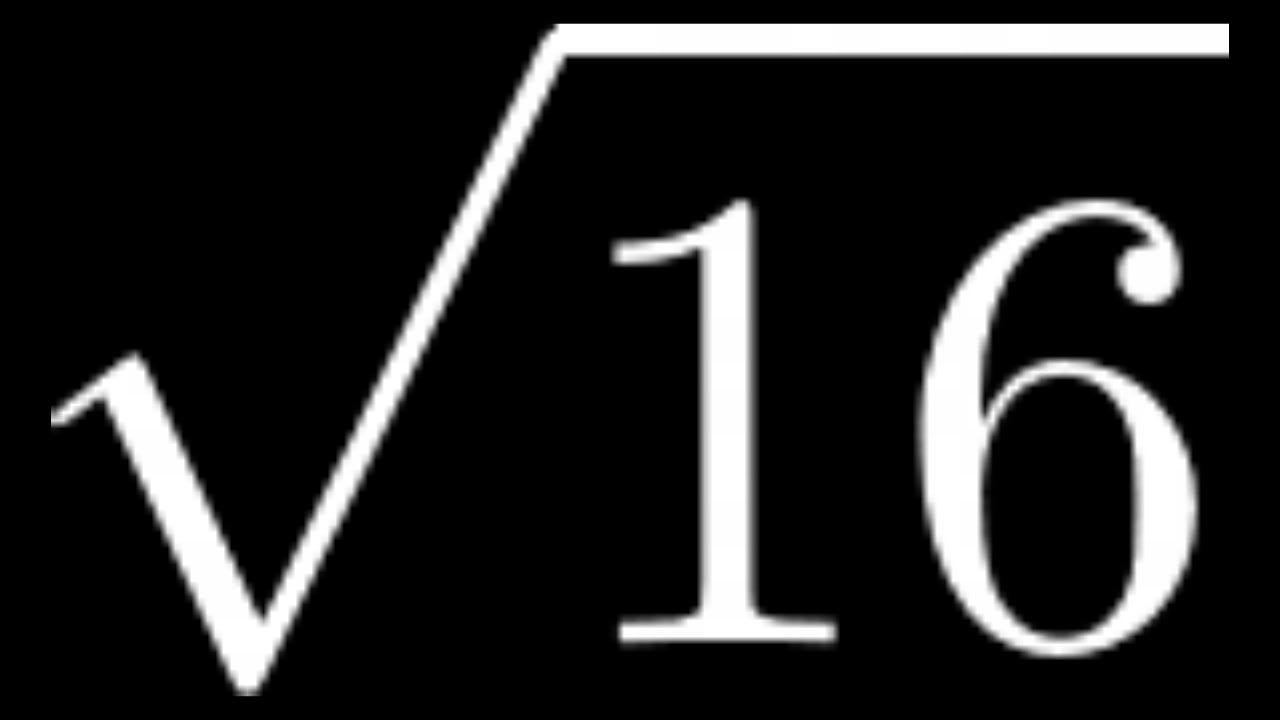
READ MORE:
Introduction to Square Roots
Square roots are mathematical functions that determine the original number which, when multiplied by itself, yields the given number. The square root symbol is denoted by √, and finding the square root of a number involves reversing the process of squaring.
For example, the square root of 16 can be expressed as:
\(\sqrt{16}\)
- First, identify the factors of 16: 1, 2, 4, 8, 16.
- Next, recognize the perfect squares among these factors: 1, 4, 16.
- Since 16 is a perfect square (4 x 4 = 16), the square root can be simplified directly.
The square root of 16 is:
\(\sqrt{16} = 4\)
Square roots can also be expressed in terms of exponents. For instance, the square root of 16 can be written as:
\(16^{\frac{1}{2}}\)
Understanding square roots is fundamental in various mathematical applications, including solving quadratic equations and simplifying radical expressions. With practice, simplifying square roots becomes an intuitive and essential skill for students and professionals alike.
Understanding Perfect Squares
Perfect squares are numbers that can be expressed as the product of an integer multiplied by itself. For example, 16 is a perfect square because it equals \(4 \times 4\). Understanding perfect squares is crucial in simplifying square roots and solving various mathematical problems.
When we simplify the square root of a perfect square, we are essentially reversing the multiplication process. The square root of a number \(x\) is a value that, when multiplied by itself, gives \(x\). For instance, \(\sqrt{16} = 4\) because \(4 \times 4 = 16\).
To recognize perfect squares, it's helpful to know some common examples:
- \(\sqrt{1} = 1\)
- \(\sqrt{4} = 2\)
- \(\sqrt{9} = 3\)
- \(\sqrt{16} = 4\)
- \(\sqrt{25} = 5\)
Simplifying the square root of a non-perfect square involves factoring the number into a product of perfect squares and other factors. For example:
- Find the factors of the number under the square root.
- Identify the perfect square factors.
- Rewrite the square root as a product of the square roots of these factors.
- Simplify the square roots of the perfect squares.
Consider the square root of 18:
- Factor 18 into \(9 \times 2\).
- Recognize that 9 is a perfect square.
- Rewrite \(\sqrt{18}\) as \(\sqrt{9 \times 2} = \sqrt{9} \times \sqrt{2}\).
- Simplify to \(3 \sqrt{2}\).
Understanding these principles helps in simplifying square roots and enhances your overall mathematical skills.
Step-by-Step Guide to Simplifying √16
Simplifying the square root of 16 involves determining the number which, when multiplied by itself, equals 16. Here is a detailed, step-by-step guide to help you understand this process:
-
Identify the Square Root: The square root of a number is a value that, when multiplied by itself, gives the original number. For 16, we are looking for a number 'x' such that \(x \times x = 16\).
-
Prime Factorization Method:
- First, find the prime factors of 16. The prime factorization of 16 is \(2 \times 2 \times 2 \times 2\), or \(2^4\).
- Rewrite the square root of 16 using its prime factors: \(\sqrt{16} = \sqrt{2^4}\).
- Simplify the expression: \(\sqrt{2^4} = 2^{4/2} = 2^2 = 4\).
-
Verification: To verify, simply multiply the result by itself: \(4 \times 4 = 16\), confirming that \(\sqrt{16} = 4\).
Thus, the square root of 16 is simplified to 4.
Mathematical Explanation and Verification
When simplifying the square root of 16, we can use basic properties of square roots and perfect squares to reach our solution. Here's a detailed, step-by-step explanation of the process:
-
Identify the number inside the square root: \( \sqrt{16} \).
-
Check if the number inside the square root is a perfect square. A perfect square is an integer that is the square of another integer. In this case, 16 is a perfect square because \( 4^2 = 16 \).
-
Rewrite the square root of 16 using the perfect square property:
$$ \sqrt{16} = \sqrt{4^2} $$
-
Simplify the square root of a perfect square. The square root of a number squared is the number itself:
$$ \sqrt{4^2} = 4 $$
Therefore, the square root of 16 simplifies to 4. To verify this result, consider squaring the answer to see if we get back to the original number:
$$ 4^2 = 16 $$
This confirms that the square root of 16 is indeed 4.
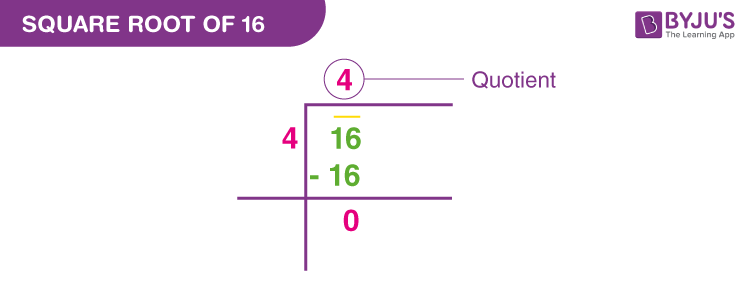
Applications of Simplifying Square Roots
Simplifying square roots is a fundamental mathematical skill with numerous applications in various fields. By reducing square roots to their simplest form, we can make complex calculations more manageable and intuitive. Here are some key applications:
- Mathematics and Algebra: Simplifying square roots is essential in solving algebraic equations, especially those involving quadratic equations and polynomial expressions. For example, solving \(x^2 = 16\) leads to \(x = \sqrt{16} = 4\).
- Geometry: Simplified square roots help in calculating distances, areas, and volumes. For instance, the diagonal of a square with a side length of 4 units can be found using the simplified square root: \(\sqrt{4^2 + 4^2} = \sqrt{32} = 4\sqrt{2}\).
- Physics and Engineering: Square roots appear frequently in formulas, such as those for calculating energy, force, and wave properties. Simplifying these roots can make the equations easier to work with. For example, in the formula for kinetic energy \(E_k = \frac{1}{2}mv^2\), if the velocity \(v\) involves a square root, simplifying it can clarify the calculations.
- Statistics: Standard deviation, a measure of data variability, involves square roots. Simplifying these roots can help in the interpretation of statistical data and results.
- Computer Science: Algorithms for graphics and data processing often use square roots. Simplifying these roots can optimize performance and resource usage.
Understanding how to simplify square roots not only aids in academic pursuits but also enhances practical problem-solving skills across a range of disciplines.
Common Mistakes and How to Avoid Them
When simplifying square roots, it's easy to make mistakes. Here are some common errors and how to avoid them:
- Incorrect factorization: Ensure you correctly factor the number under the square root. For example, the square root of 16 should be factored as \( \sqrt{4^2} \), not \( \sqrt{8 \times 2} \).
- Ignoring negative roots: Remember that square roots can be both positive and negative. For instance, \( \sqrt{16} = \pm 4 \).
- Incorrect application of the product rule: When simplifying \( \sqrt{ab} \), make sure you apply \( \sqrt{a} \times \sqrt{b} \). For example, \( \sqrt{25 \times 4} = \sqrt{25} \times \sqrt{4} = 5 \times 2 = 10 \).
- Overlooking simplest form: Always reduce the square root to its simplest form. For instance, simplify \( \sqrt{50} \) to \( 5\sqrt{2} \) rather than leaving it as \( \sqrt{50} \).
- Misapplying the quotient rule: For \( \sqrt{\frac{a}{b}} \), correctly use \( \frac{\sqrt{a}}{\sqrt{b}} \). An example is \( \sqrt{\frac{9}{4}} = \frac{\sqrt{9}}{\sqrt{4}} = \frac{3}{2} \).
By understanding and avoiding these common mistakes, you can simplify square roots accurately and efficiently.
Advanced Concepts Related to Square Roots
Understanding square roots goes beyond simply simplifying them. Here are some advanced concepts related to square roots that will deepen your mathematical knowledge:
1. Irrational Numbers
Not all square roots simplify to integers. Some square roots are irrational numbers, which cannot be expressed as a simple fraction. For example, √2 is an irrational number.
Mathematically, irrational numbers are those that cannot be written as a ratio of two integers. Their decimal expansions are non-repeating and non-terminating.
2. Simplifying Higher-Order Roots
In addition to square roots, there are cube roots, fourth roots, and so on. The principles of simplifying these roots are similar but involve higher powers. For instance, to simplify ∛27:
\[ \sqrt[3]{27} = 3 \]
This is because \( 3^3 = 27 \).
3. Using Rational Exponents
Square roots can also be expressed using rational exponents. For example, √16 can be written as \( 16^{1/2} \). This notation is particularly useful in algebra and calculus.
More generally, \( \sqrt[n]{a} \) can be written as \( a^{1/n} \).
4. Complex Numbers and Square Roots
When dealing with negative numbers under the square root, we enter the realm of complex numbers. The square root of a negative number involves the imaginary unit \( i \), where \( i^2 = -1 \). For example:
\[ \sqrt{-16} = 4i \]
5. Properties of Square Roots
- Product Property: \(\sqrt{a} \cdot \sqrt{b} = \sqrt{a \cdot b}\)
- Quotient Property: \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
6. Square Root Functions
The square root function \( f(x) = \sqrt{x} \) is a specific type of function with its own properties. It is a one-to-one function, meaning each input has a unique output, and it only takes non-negative values of \( x \).
Graphically, it produces a curve starting from the origin (0, 0) and increases slowly as \( x \) increases.

7. Historical Context and Applications
Square roots have a rich history in mathematics and are used in various fields such as engineering, physics, and computer science. Understanding their properties and applications can provide deeper insights into problem-solving and analytical thinking.
8. Practice Problems
Here are some advanced practice problems to test your understanding:
- Simplify \( \sqrt{50} \)
- Express \( \sqrt[3]{125} \) using rational exponents
- Calculate \( \sqrt{-25} \)
- Prove that \( \sqrt{a^2} = |a| \) for any real number \( a \)
Answers:
- \( \sqrt{50} = 5\sqrt{2} \)
- \( \sqrt[3]{125} = 125^{1/3} = 5 \)
- \( \sqrt{-25} = 5i \)
- \( \sqrt{a^2} = |a| \) by definition of absolute value and properties of square roots.
Practice Problems and Solutions
Practice simplifying square roots with these example problems and detailed solutions. Use the concepts you've learned to solve these problems step-by-step.
-
Simplify \( \sqrt{25} \)
Solution:
- Step 1: Identify that 25 is a perfect square.
- Step 2: \( 25 = 5 \times 5 \)
- Step 3: Therefore, \( \sqrt{25} = 5 \)
-
Simplify \( \sqrt{72} \)
Solution:
- Step 1: Factor 72 into its prime factors: \( 72 = 2^3 \times 3^2 \)
- Step 2: Apply the square root to each factor: \( \sqrt{72} = \sqrt{2^3 \times 3^2} \)
- Step 3: Simplify by separating the factors: \( \sqrt{2^3} \times \sqrt{3^2} = 2\sqrt{2} \times 3 \)
- Step 4: Combine the terms: \( 6\sqrt{2} \)
-
Simplify \( \sqrt{50} \)
Solution:
- Step 1: Factor 50 into its prime factors: \( 50 = 2 \times 5^2 \)
- Step 2: Apply the square root to each factor: \( \sqrt{50} = \sqrt{2 \times 5^2} \)
- Step 3: Simplify by separating the factors: \( \sqrt{2} \times \sqrt{5^2} = \sqrt{2} \times 5 \)
- Step 4: Combine the terms: \( 5\sqrt{2} \)
-
Simplify \( \sqrt{45} \)
Solution:
- Step 1: Factor 45 into its prime factors: \( 45 = 3^2 \times 5 \)
- Step 2: Apply the square root to each factor: \( \sqrt{45} = \sqrt{3^2 \times 5} \)
- Step 3: Simplify by separating the factors: \( \sqrt{3^2} \times \sqrt{5} = 3\sqrt{5} \)
-
Simplify \( \sqrt{98} \)
Solution:
- Step 1: Factor 98 into its prime factors: \( 98 = 2 \times 7^2 \)
- Step 2: Apply the square root to each factor: \( \sqrt{98} = \sqrt{2 \times 7^2} \)
- Step 3: Simplify by separating the factors: \( \sqrt{2} \times \sqrt{7^2} = \sqrt{2} \times 7 \)
- Step 4: Combine the terms: \( 7\sqrt{2} \)
-
Simplify \( 2\sqrt{12} + 3\sqrt{27} \)
Solution:
- Step 1: Simplify each term separately: \( 2\sqrt{12} = 2 \times 2\sqrt{3} = 4\sqrt{3} \) and \( 3\sqrt{27} = 3 \times 3\sqrt{3} = 9\sqrt{3} \)
- Step 2: Combine like terms: \( 4\sqrt{3} + 9\sqrt{3} = 13\sqrt{3} \)

Additional Resources and Tools
For further exploration and practice in simplifying square roots, the following resources and tools can be highly beneficial:
-
Online Calculators
- - Offers a comprehensive calculator that can simplify square roots and other algebraic expressions. It provides step-by-step solutions, making it easier to understand the process.
- - A versatile calculator that helps in simplifying square roots and solving a wide range of mathematical problems. It's user-friendly and gives detailed explanations.
-
Video Tutorials
- - Khan Academy offers numerous free video tutorials on simplifying square roots and related concepts. These videos are excellent for visual learners who need to see each step in action.
- - This YouTube channel provides clear and concise explanations on various mathematical topics, including square roots. The tutorials are easy to follow and highly informative.
-
Practice Worksheets and Problems
- - A great resource for printable worksheets that cover a wide range of math topics, including square roots. These worksheets provide ample practice and come with answer keys for self-assessment.
- - An online platform that offers practice problems and interactive exercises on square roots and other math concepts. It provides instant feedback and tracks your progress.
-
Interactive Tools and Apps
- - Desmos offers an online graphing calculator that is excellent for visualizing and exploring mathematical concepts, including square roots. It's an interactive tool that can help deepen understanding.
- - This computational engine can simplify square roots and provide detailed explanations. It's a powerful tool for solving complex mathematical problems.
Conclusion
In conclusion, simplifying the square root of 16 is a straightforward process, as 16 is a perfect square. We learned that:
- The square root of 16 is 4, because 4 multiplied by itself equals 16.
- We can express this as \( \sqrt{16} = 4 \).
- This concept is crucial in algebra and many other fields of mathematics, making calculations simpler and more efficient.
Understanding how to simplify square roots helps build a foundation for more advanced mathematical concepts and problem-solving techniques. By mastering this basic skill, you are better equipped to tackle more complex equations and appreciate the beauty of mathematics.
We hope this guide has provided a clear and comprehensive understanding of how to simplify square roots and highlighted the importance of this fundamental mathematical operation.
Hướng dẫn cách đơn giản hóa căn bậc hai của 16: sqrt(16). Video này sẽ giúp bạn hiểu rõ hơn về cách tính toán và ứng dụng của căn bậc hai trong toán học.
Cách Đơn Giản Hóa Căn Bậc Hai của 16: sqrt(16)
READ MORE:
Video này giải thích cách tìm căn bậc hai của 16. Khám phá cách tính toán và ứng dụng của căn bậc hai trong toán học.
Căn Bậc Hai của 16