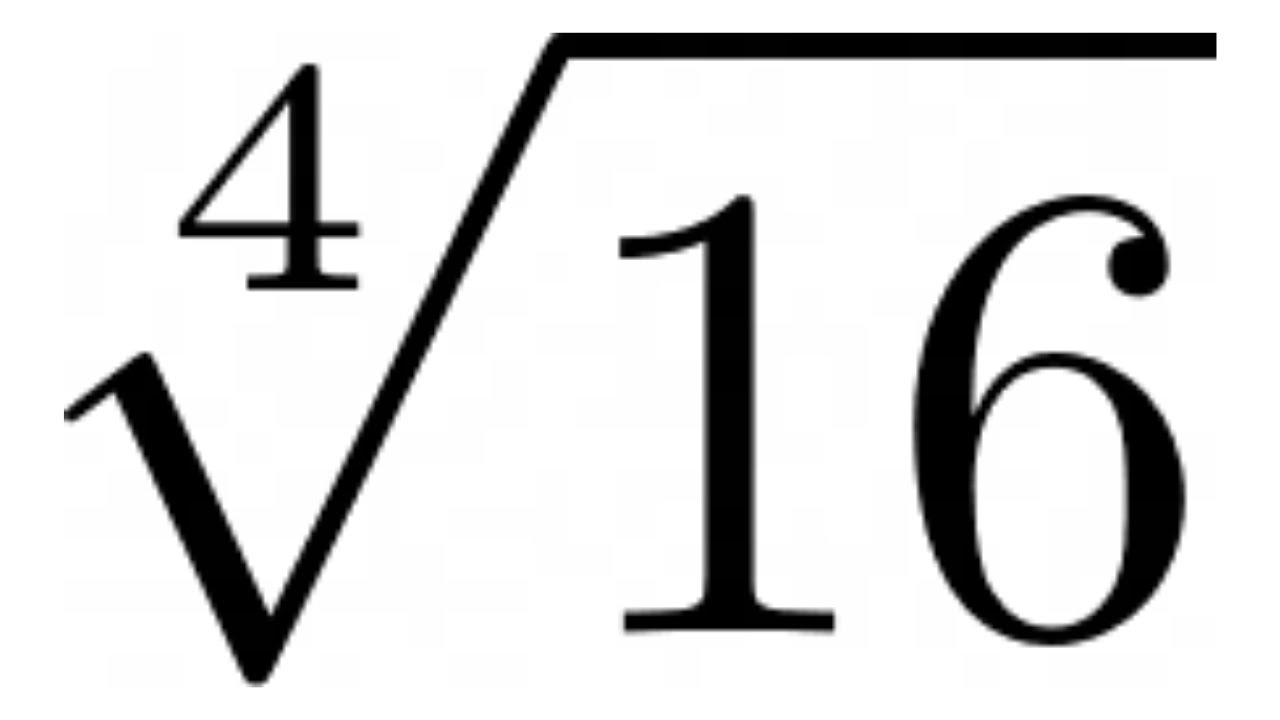Topic square root of negative 16: The square root of negative 16, denoted as √-16, introduces the concept of imaginary numbers. In mathematics, the square root of -16 is represented as ±4i, where 'i' is the imaginary unit. This intriguing topic delves into complex numbers and their applications, making it a fascinating subject for those interested in advanced mathematics.
Table of Content
- Understanding the Square Root of -16
- Understanding the Square Root of Negative 16
- Definition of Square Root
- Imaginary Numbers and the Complex Plane
- Calculating the Square Root of -16
- Properties of Square Roots of Negative Numbers
- Simplifying Square Roots of Negative Numbers
- Examples and Applications
- YOUTUBE:
Understanding the Square Root of -16
The square root of a negative number is not a real number. Instead, it is a complex number. For example, the square root of -16 is calculated as follows:
Mathematical Explanation
The square root of -16 can be represented using imaginary numbers. The imaginary unit is denoted as i, where i is defined as the square root of -1. Therefore, the square root of -16 can be expressed as:
\( \sqrt{-16} = \sqrt{16 \cdot (-1)} = \sqrt{16} \cdot \sqrt{-1} = 4i \)
Steps to Simplify \( \sqrt{-16} \)
- Identify the negative sign inside the square root.
- Separate the negative sign and express it as \( \sqrt{-1} \).
- Simplify the remaining positive number under the square root.
- Combine the results: \( \sqrt{-16} = 4i \).
Complex Numbers and Imaginary Units
In complex number terms, \( 4i \) is an imaginary number where:
- i is the imaginary unit.
- \( 4 \) is the real number coefficient.
Applications of Imaginary Numbers
Imaginary numbers, such as \( 4i \), are used in various fields including engineering, physics, and applied mathematics to solve equations that do not have real solutions.
Examples
Here are some other examples of square roots of negative numbers:
| Radicand | Square Root |
|---|---|
| -20 | ±4.472i |
| -18 | ±4.243i |
| -16 | ±4i |
| -14 | ±3.742i |
Conclusion
To sum up, the square root of -16 is a complex number: \( \pm 4i \). This indicates that the original problem does not have a solution in the set of real numbers but instead in the set of complex numbers.

READ MORE:
Understanding the Square Root of Negative 16
The square root of negative 16 is an intriguing concept in mathematics, as it involves the imaginary unit, denoted by \(i\), which is defined as \(i = \sqrt{-1}\). To find the square root of -16, we use this property of imaginary numbers.
Here's a step-by-step process to understand this:
- First, express -16 as the product of 16 and -1:
- \(-16 = 16 \times (-1)\)
- Next, take the square root of both components:
- \(\sqrt{-16} = \sqrt{16 \times (-1)}\)
- Apply the property of square roots to separate the factors:
- \(\sqrt{16 \times (-1)} = \sqrt{16} \times \sqrt{-1}\)
- Calculate the square root of 16 and use the definition of \(i\):
- \(\sqrt{16} = 4\)
- \(\sqrt{-1} = i\)
- Combine these results:
- \(\sqrt{-16} = 4i\)
Therefore, the square root of -16 is \(4i\), an imaginary number. This approach demonstrates how we use the imaginary unit to handle the square roots of negative numbers effectively.
Definition of Square Root
The square root of a number is a value that, when multiplied by itself, gives the original number. For instance, the square root of 16 is 4 because 4 multiplied by 4 equals 16. The square root operation is denoted by the radical symbol (√).
In mathematical terms, the square root of a number \( x \) is a number \( y \) such that \( y^2 = x \). This can be expressed as:
\[
\sqrt{x} = y \quad \text{if and only if} \quad y^2 = x
\]
For non-negative numbers, there are two square roots: a positive and a negative root. For example:
- The square root of 9 is \( \pm3 \) because \( 3^2 = 9 \) and \( (-3)^2 = 9 \).
- The square root of 25 is \( \pm5 \) because \( 5^2 = 25 \) and \( (-5)^2 = 25 \).
However, when dealing with negative numbers, such as -16, the square root involves complex numbers. The square root of a negative number \( -x \) is expressed using imaginary numbers. The imaginary unit \( i \) is defined as \( \sqrt{-1} \), and thus:
\[
\sqrt{-16} = 4i \quad \text{and} \quad \sqrt{-16} = -4i
\]
In general, for any negative number \(-x\), the square root can be written as:
\[
\sqrt{-x} = \pm i\sqrt{x}
\]
Where \( i \) is the imaginary unit.
Imaginary Numbers and the Complex Plane
Imaginary numbers are used to represent the square roots of negative numbers, which are not possible within the realm of real numbers. The square root of negative 16 is a classic example, leading us into the concept of imaginary and complex numbers.
The imaginary unit is denoted as i, where \( i = \sqrt{-1} \). Using this, the square root of -16 can be expressed as:
\[ \sqrt{-16} = \sqrt{16} \times \sqrt{-1} = 4i \]
Imaginary numbers, such as \( 4i \), do not have a place on the traditional number line. Instead, they are represented on the complex plane. The complex plane is a two-dimensional plane where the x-axis represents the real part of a complex number and the y-axis represents the imaginary part.
A complex number is in the form \( a + bi \), where \( a \) and \( b \) are real numbers. For example, \( 3 + 4i \) is a complex number with a real part of 3 and an imaginary part of 4.
Steps to Plot Complex Numbers on the Complex Plane:
- Identify the real part of the complex number and plot it on the x-axis.
- Identify the imaginary part and plot it on the y-axis.
- Combine these coordinates to place the complex number on the plane.
Let's plot the complex number \( 3 + 4i \) as an example:
- Real part: 3 (x-axis)
- Imaginary part: 4 (y-axis)
- Plot the point at (3, 4) on the complex plane.
By using imaginary numbers and the complex plane, we can perform arithmetic operations on complex numbers, solve quadratic equations with negative discriminants, and explore various fields of engineering and physics where these concepts are essential.
Calculating the Square Root of -16
To calculate the square root of -16, we need to understand the concept of imaginary numbers, as the square root of a negative number is not a real number. The imaginary unit, denoted as i, is defined as the square root of -1.
Here's the step-by-step process to find the square root of -16:
- First, express -16 in terms of its positive counterpart and the imaginary unit:
- Next, use the property of square roots to separate the terms:
- Apply the square root to each term individually:
- We know that √16 = 4 and √(-1) = i:
-16 can be written as 16 * -1.
√(-16) = √(16 * -1)
√(16 * -1) = √16 * √(-1)
Therefore, √(16 * -1) = 4 * i = 4i
So, the square root of -16 is 4i.

Properties of Square Roots of Negative Numbers
When dealing with square roots of negative numbers, we enter the realm of complex numbers. Here are the key properties:
- Imaginary Unit: The imaginary unit \( i \) is defined as \( \sqrt{-1} \). This forms the basis for handling square roots of negative numbers.
- Square Root Representation: For any positive real number \( a \), the square root of -a is represented as \( \sqrt{-a} = i\sqrt{a} \). For example, \( \sqrt{-16} = 4i \).
- Principal Square Root: The principal square root of a negative number is the positive imaginary number. Hence, the principal square root of -16 is \( 4i \).
- Multiple Roots: A negative number has two square roots: one positive and one negative. For \( -16 \), these are \( 4i \) and \( -4i \).
- Non-real Roots: Square roots of negative numbers do not exist in the set of real numbers. They are purely imaginary or complex.
Here is a table illustrating the square roots of some negative numbers:
| Radicand | Square Root Symbol | Value |
|---|---|---|
| -16 | \(\sqrt{-16}\) | ±4i |
| -9 | \(\sqrt{-9}\) | ±3i |
| -4 | \(\sqrt{-4}\) | ±2i |
| -1 | \(\sqrt{-1}\) | ±i |
In summary, the square roots of negative numbers are complex, involving the imaginary unit \( i \). Understanding these properties is essential for advanced mathematical concepts and applications.
Simplifying Square Roots of Negative Numbers
To simplify the square roots of negative numbers, we use the concept of imaginary numbers. Imaginary numbers are essential in dealing with the square roots of negative values because the square root of a negative number is not defined within the set of real numbers. Here are the steps to simplify square roots of negative numbers:
- Identify the negative number under the square root. For example, let's consider the square root of -16.
- Rewrite the negative number as the product of -1 and the positive counterpart of the number. In our example, -16 can be written as \( -1 \times 16 \).
- Use the property of square roots that \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \). This allows us to separate the square root of -1 from the square root of 16: \[ \sqrt{-16} = \sqrt{-1 \times 16} = \sqrt{-1} \times \sqrt{16} \]
- Recognize that the square root of -1 is defined as the imaginary unit \( i \): \[ \sqrt{-1} = i \]
- Simplify the remaining square root. For \( \sqrt{16} \), we get 4: \[ \sqrt{16} = 4 \]
- Combine the results to express the simplified form: \[ \sqrt{-16} = i \times 4 = 4i \]
Thus, the square root of -16 simplifies to \( 4i \). This method can be applied to any negative number under the square root by following these steps:
- Rewrite the number as the product of -1 and its positive counterpart.
- Use the properties of square roots to separate the terms.
- Replace the square root of -1 with \( i \).
- Simplify the remaining square root of the positive number.
This approach ensures that all square roots of negative numbers are correctly expressed in terms of imaginary numbers, making them manageable within the context of complex numbers.
Examples and Applications
Imaginary numbers, although abstract, have various practical applications in different fields. Understanding their examples and applications helps appreciate their significance in both theoretical and applied mathematics.
Examples of Square Roots of Negative Numbers
- Square Root of -1: The most fundamental example is \( \sqrt{-1} \), which is defined as \( i \).
- Square Root of -4: To find the square root of -4, we calculate \( \sqrt{4} = 2 \) and then multiply by \( i \) to get \( 2i \).
- Square Root of -9: Similarly, the square root of -9 is \( 3i \), since \( (3i)^2 = -9 \).
- Square Root of -16: For -16, the square root is \( 4i \), as \( (4i)^2 = -16 \).
- Square Root of -25: The square root of -25 is \( 5i \), because \( (5i)^2 = -25 \).
Applications of Imaginary Numbers in Real Life
Imaginary numbers play a crucial role in various fields, enabling complex analysis and problem-solving.
- Electrical Engineering: Imaginary numbers are used to analyze electrical circuits. Impedance, combining resistance and reactance, relies on complex numbers to describe the phase difference between voltage and current.
- Signal Processing: In signal processing, imaginary numbers facilitate the analysis of signals, particularly in Fourier transforms. This is crucial in telecommunications, audio engineering, and image processing.
- Quantum Mechanics: Complex numbers are essential in quantum mechanics to describe quantum states and probabilities. They are used in the representation of wave functions.
- Control Theory: Imaginary numbers help in the stability analysis of systems. Using the Laplace transform, which incorporates complex numbers, engineers design systems with predictable responses under various conditions.
- Fluid Dynamics: Complex analysis assists in solving fluid flow problems, especially in potential flow theory, where the complex potential function provides insights into flow patterns around objects.
These applications highlight the importance of imaginary numbers beyond theoretical mathematics. They provide precise analysis and innovative solutions in science and engineering, demonstrating the beauty and utility of mathematical concepts in understanding and shaping the world around us.
Căn bậc hai của -16 || Căn bậc hai của một số âm || Căn(-16) || Căn của số âm 16
READ MORE:
Nhân Căn Bậc Hai của Số Âm