Topic square root of 1/64: The square root of 1/64 is a fundamental concept in mathematics that can be simplified to 1/8. Understanding how to find and simplify this square root provides valuable insight into working with fractions and radicals. This article explores the step-by-step process, practical applications, and common mistakes to avoid when calculating square roots.
Table of Content
- Square Root of 1/64
- Introduction to Square Roots
- Simplifying the Square Root of 1/64
- Calculation Methods
- Examples of Square Root Calculations
- Common Mistakes and How to Avoid Them
- Using Calculators for Square Roots
- Square Roots of Perfect Squares
- Square Roots of Imperfect Squares
- Real-life Applications of Square Roots
- YOUTUBE:
Square Root of 1/64
The square root of a fraction can be determined by taking the square root of the numerator and the denominator separately. Let's solve for the square root of step by step.
Steps to Find the Square Root
- Start with the fraction .
- Rewrite the square root of the fraction as the fraction of the square roots: .
- Simplify the square roots in the numerator and the denominator:
- The square root of 1 is 1.
- The square root of 64 is 8.
- Therefore, the square root of is , which can also be written as 0.125.
Summary
Thus, the square root of is , which simplifies to 0.125.
Further Examples
- The square root of is .
- The square root of is .
References
- Mathway: Simplify square root of 1/64
- Microsoft Math Solver: Solve sqrt(1/64)
- Brainly: What is the square root of 1/64

READ MORE:
Introduction to Square Roots
The concept of square roots is fundamental in mathematics. A square root of a number \( x \) is a number \( y \) such that \( y^2 = x \). This means that \( y \), when multiplied by itself, results in \( x \). The principal square root is the nonnegative square root, denoted as \( \sqrt{x} \).
For example, the square root of 9 is 3, because \( 3^2 = 9 \). Similarly, the square root of 1/64 can be calculated by taking the square root of both the numerator and the denominator separately:
- \( \sqrt{\frac{1}{64}} = \frac{\sqrt{1}}{\sqrt{64}} \)
- \( \sqrt{1} = 1 \)
- \( \sqrt{64} = 8 \)
- Therefore, \( \sqrt{\frac{1}{64}} = \frac{1}{8} \)
This simplification shows that the square root of 1/64 is 1/8. Understanding square roots is essential for solving various algebraic equations and applying mathematical principles in real-life scenarios.
Simplifying the Square Root of 1/64
Simplifying the square root of
-
Rewrite the Expression: Begin by expressing the square root of the fraction as the division of the square roots of the numerator and the denominator:
\(\sqrt{\frac{1}{64}} = \frac{\sqrt{1}}{\sqrt{64}}\) -
Evaluate the Square Roots: Calculate the square roots of the numerator and the denominator separately:
\(\sqrt{1} = 1\) \(\sqrt{64} = 8\)
-
Form the Simplified Expression: Combine the results of the square roots to form the simplified fraction:
\(\frac{1}{8}\)
Thus, the square root of
Calculation Methods
Calculating the square root of a fraction such as 1/64 involves several steps. Here are the detailed methods to simplify and calculate this value:
-
Rewrite the Fraction:
Start by rewriting the square root of the fraction as a quotient of two separate square roots:
\[\sqrt{\frac{1}{64}} = \frac{\sqrt{1}}{\sqrt{64}}\]
-
Simplify the Numerator and Denominator:
Next, calculate the square root of the numerator and the denominator individually:
- \(\sqrt{1} = 1\)
- \(\sqrt{64} = 8\)
This gives us:
\[\frac{\sqrt{1}}{\sqrt{64}} = \frac{1}{8}\]
-
Final Result:
Therefore, the square root of 1/64 simplifies to:
\[\sqrt{\frac{1}{64}} = \frac{1}{8} = 0.125\]
By following these steps, we can accurately determine the square root of any fraction, including 1/64. This method ensures clarity and precision in mathematical calculations.
Examples of Square Root Calculations
Calculating square roots can be straightforward when dealing with perfect squares but might seem challenging with fractions or non-perfect squares. Here, we will explore examples, including the square root of 1/64, to illustrate the process.
- Square Root of a Perfect Square:
The square root of 16 is 4 because \( 4 \times 4 = 16 \).
- Square Root of a Fraction:
To find the square root of \( \frac{1}{64} \):
- Rewrite the fraction under the square root as the square root of the numerator divided by the square root of the denominator:
\( \sqrt{\frac{1}{64}} = \frac{\sqrt{1}}{\sqrt{64}} \). - Calculate the square root of the numerator and the denominator separately:
\( \sqrt{1} = 1 \) and \( \sqrt{64} = 8 \). - Combine the results to get the simplified square root:
\( \frac{1}{8} \). - So, \( \sqrt{\frac{1}{64}} = \frac{1}{8} \).
- Rewrite the fraction under the square root as the square root of the numerator divided by the square root of the denominator:
- Square Root of a Non-Perfect Square:
For example, the square root of 10:
- Estimate the value: 3 is less than \( \sqrt{10} \) but 4 is more. So, \( \sqrt{10} \) is between 3 and 4.
- Refine the estimate using a method like averaging: \( \sqrt{10} \approx 3.162 \).
- Square Root of a Negative Number:
Square roots of negative numbers involve imaginary numbers. For instance, \( \sqrt{-9} = 3i \), where \( i \) is the imaginary unit with \( i^2 = -1 \).

Common Mistakes and How to Avoid Them
When working with square roots, especially with fractions like \( \sqrt{\frac{1}{64}} \), it's important to avoid common pitfalls. Below are some typical mistakes and tips on how to steer clear of them:
-
Mistake 1: Incorrect Simplification
One common error is to simplify the square root of a fraction incorrectly. For instance, students might incorrectly simplify \( \sqrt{\frac{1}{64}} \) as \( \frac{1}{\sqrt{64}} \) instead of \( \frac{\sqrt{1}}{\sqrt{64}} \).
How to avoid: Remember to separate the square root of the numerator and the denominator, then simplify each part individually: \( \sqrt{\frac{1}{64}} = \frac{\sqrt{1}}{\sqrt{64}} = \frac{1}{8} \).
-
Mistake 2: Neglecting the Sign
Another mistake is forgetting that square roots can have both positive and negative values. For example, \( \sqrt{64} \) is both 8 and -8.
How to avoid: Always consider both the principal (positive) and negative roots when solving equations involving square roots.
-
Mistake 3: Misapplying the Product Rule
Students sometimes incorrectly apply the product rule for square roots. For example, they might incorrectly simplify \( \sqrt{a \cdot b} \) as \( \sqrt{a} \cdot \sqrt{b} \) without considering that this only holds true when both \( a \) and \( b \) are non-negative.
How to avoid: Ensure that both numbers under the square root are non-negative before applying the product rule: \( \sqrt{ab} = \sqrt{a} \cdot \sqrt{b} \).
-
Mistake 4: Incorrectly Handling Complex Numbers
Some students forget that the square root of a negative number involves complex numbers.
How to avoid: Remember that \( \sqrt{-a} = i\sqrt{a} \) where \( i \) is the imaginary unit, and \( a \) is a positive real number.
-
Mistake 5: Forgetting the Absolute Value
When simplifying expressions involving variables, students often forget to include absolute value signs where necessary. For instance, \( \sqrt{x^2} = |x| \), not simply \( x \).
How to avoid: Always use absolute value to account for both positive and negative values of the variable: \( \sqrt{x^2} = |x| \).
Using Calculators for Square Roots
Calculators are essential tools for calculating square roots efficiently and accurately. There are various types of calculators that can be used, including graphing calculators and scientific calculators. Below are detailed steps on how to use these calculators to find the square root of 1/64.
Graphing Calculators
Graphing calculators are powerful tools that can handle complex mathematical operations. Here’s how to use them to find the square root of 1/64:
- Turn on the graphing calculator.
- Access the square root function. This is usually represented by the symbol √ or can be found in the calculator's math menu.
- Enter the fraction 1/64. You might need to use parentheses to ensure the fraction is entered correctly, like this: (1/64).
- Press the "Enter" or "=" button to calculate the result.
- The display will show the square root of 1/64, which is 1/8 or 0.125.
Scientific Calculators
Scientific calculators are widely used for their convenience and functionality. Follow these steps to calculate the square root of 1/64:
- Turn on the scientific calculator.
- Press the square root button (√). On some calculators, you might need to press the "Shift" or "2nd" button first to access the square root function.
- Input the fraction 1/64. Ensure you use parentheses if needed, like this: (1/64).
- Press the "=" button to get the result.
- The calculator will display the square root of 1/64 as 0.125 or 1/8.
Using calculators to find square roots simplifies the process and helps avoid common calculation errors. Whether using a graphing or a scientific calculator, these steps will help you efficiently find the square root of any number, including 1/64.
Square Roots of Perfect Squares
A perfect square is a number that is the square of an integer. The square root of a perfect square is always an integer or a simple fraction. Let's explore some examples and properties of perfect squares and their square roots.
Understanding Perfect Squares
Perfect squares are the results of multiplying a number by itself. For example, 1, 4, 9, 16, 25, and so on are perfect squares because:
- 1 = 1 × 1
- 4 = 2 × 2
- 9 = 3 × 3
- 16 = 4 × 4
- 25 = 5 × 5
Square Roots of Perfect Squares
The square root of a perfect square is straightforward to calculate because it is the original number used to create the square. Here are some examples:
| Perfect Square | Square Root |
|---|---|
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
| 36 | 6 |
| 49 | 7 |
| 64 | 8 |
| 81 | 9 |
| 100 | 10 |
Fractional Perfect Squares
Perfect squares can also be fractions. To find the square root of a perfect square fraction, take the square root of the numerator and the denominator separately. For example:
- \(\sqrt{\frac{1}{64}} = \frac{\sqrt{1}}{\sqrt{64}} = \frac{1}{8}\)
- \(\sqrt{\frac{4}{9}} = \frac{\sqrt{4}}{\sqrt{9}} = \frac{2}{3}\)
Properties of Perfect Squares
Perfect squares have several unique properties:
- They are always non-negative.
- The square root of a perfect square is always rational.
- If a number is a perfect square, its last digit must be 0, 1, 4, 5, 6, or 9.
Visualizing Perfect Squares
Perfect squares can be visualized as square grids. For example, a 3 × 3 grid represents the number 9:
| 1 | 1 | 1 | ||||
| 1 | 1 | 1 | ||||
| 1 | 1 | 1 |
This visual aid helps in understanding why the square root of 9 is 3.
In summary, understanding the concept of perfect squares and their square roots is fundamental in algebra and mathematics. They provide a basis for more complex mathematical concepts and applications.
Square Roots of Imperfect Squares
Imperfect squares are numbers that are not the square of an integer. Their square roots are often irrational and cannot be expressed as a simple fraction or integer. Calculating the square root of an imperfect square involves approximation methods or the use of calculators. Let's explore how to find and understand the square roots of imperfect squares.
Examples of Imperfect Squares
Here are some examples of imperfect squares and their approximate square roots:
| Imperfect Square | Approximate Square Root |
|---|---|
| 2 | 1.414 |
| 3 | 1.732 |
| 5 | 2.236 |
| 7 | 2.646 |
| 10 | 3.162 |
| 15 | 3.873 |
| 20 | 4.472 |
Methods to Approximate Square Roots
There are various methods to approximate the square root of an imperfect square:
- Long Division Method: This manual method involves a process similar to long division, providing decimal approximations of square roots.
- Estimation and Averaging: Start with a rough estimate and improve it by averaging. For example, to find \(\sqrt{10}\):
- Estimate a number between which the square root lies (e.g., between 3 and 4).
- Average 3 and 4: \(\frac{3 + 4}{2} = 3.5\).
- Check if 3.5 is close by squaring it (\(3.5^2 = 12.25\)), and adjust accordingly.
- Continue refining: average between 3 and 3.5, and so on.
- Using Calculators: Most modern calculators can compute the square root to several decimal places, providing quick and accurate results.
Properties of Square Roots of Imperfect Squares
The square roots of imperfect squares have unique properties:
- They are often irrational, meaning they cannot be exactly expressed as a fraction.
- They are non-repeating, non-terminating decimals.
- They can be approximated to any desired degree of accuracy.
Visualizing Imperfect Squares
Imperfect squares can be visualized using a number line or graph. For example, the square root of 2 can be approximated on a number line between 1 and 2:
| 0 | 1 | 1.4 | 1.41 | 1.414 | 2 | 3 |
This demonstrates how \(\sqrt{2} \approx 1.414\) falls between 1 and 2 on the number line.
Understanding the square roots of imperfect squares helps in dealing with more complex mathematical problems and real-life applications. It also enhances our comprehension of irrational numbers and their properties.
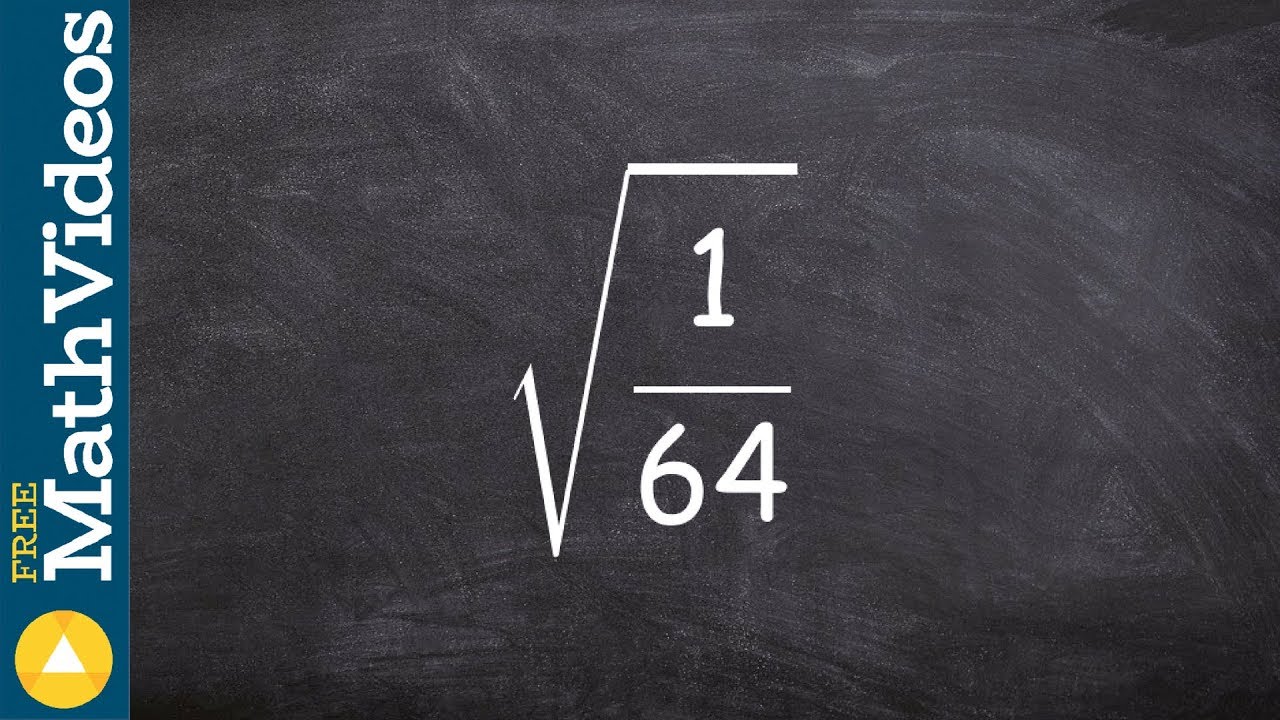
Real-life Applications of Square Roots
Square roots play a crucial role in various real-life scenarios and practical applications. They are used in fields ranging from architecture and engineering to finance and physics. Understanding how to calculate and apply square roots helps solve numerous problems in everyday life and professional tasks.
1. Geometry and Construction
Square roots are fundamental in geometry, especially in calculating dimensions and distances. For example:
- Pythagorean Theorem: In a right-angled triangle, the length of the hypotenuse (\(c\)) can be found using the square root of the sum of the squares of the other two sides (\(a\) and \(b\)): \[ c = \sqrt{a^2 + b^2} \] This principle is crucial in construction and design, where accurate measurements are essential.
- Area Calculation: To find the side length of a square given its area, you use the square root. For instance, if a square has an area of 64 square units, its side length is: \[ \text{Side length} = \sqrt{64} = 8 \]
2. Physics and Engineering
In physics and engineering, square roots are used to calculate various parameters, such as:
- Velocity and Acceleration: In kinematic equations, the square root is often used to solve for time or distance under constant acceleration.
- Wave Frequencies: The relationship between wave speed (\(v\)), frequency (\(f\)), and wavelength (\(\lambda\)) often involves square roots, especially in sound and light wave calculations: \[ v = f \times \lambda \]
- Stress and Strain: In material science, the square root is used to relate stress and strain in materials, which is crucial for understanding material strength and deformation.
3. Finance and Economics
Square roots are used in finance to calculate interest rates, investment returns, and risk assessments:
- Compound Interest: The formula for compound interest involves square roots when solving for the interest rate or time period. For example, to find the annual interest rate (\(r\)) required to double an investment (\(P\)) over \(n\) years: \[ r = \left( \sqrt[n]{\frac{A}{P}} - 1 \right) \times 100 \] where \(A\) is the final amount.
- Standard Deviation: In statistics, the standard deviation of a dataset involves the square root and is used to measure the dispersion of data points from the mean.
4. Medicine and Biology
Square roots are also important in medical and biological research:
- Dosage Calculations: Medication dosages are often calculated using square roots, especially when adjusting for body surface area (BSA) in pharmacology.
- Growth Rates: Biological growth rates, such as population growth, can be modeled using equations involving square roots to estimate future sizes or generations.
5. Computer Graphics and Gaming
In computer graphics and gaming, square roots are used to calculate distances and scaling factors:
- Distance Calculation: The Euclidean distance between two points in a 2D or 3D space is calculated using the square root: \[ \text{Distance} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2} \] This is essential for rendering scenes, collision detection, and character movement in virtual environments.
- Scaling and Rotation: Transformations involving scaling and rotating objects in computer graphics often use square roots to maintain proportions and achieve smooth animations.
Conclusion
Square roots are integral to numerous aspects of daily life and various professional fields. Their application ranges from solving geometric problems to analyzing financial data, and they are indispensable tools in scientific and technological advancements.
Học cách tính căn bậc hai của phân số, căn(1/64)
READ MORE:
Đơn giản hóa Căn Bậc Hai với Phân Số: căn(1/64)