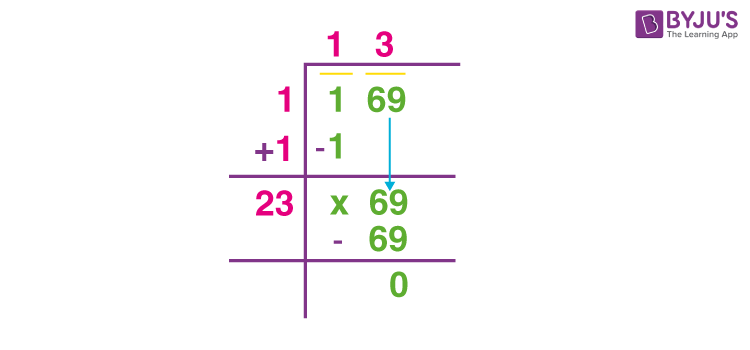
Topic square root of 4/16: The square root of 4/16 is a straightforward calculation that simplifies to a simple fraction. This guide will walk you through the steps to find the square root of this fraction, understand the underlying principles, and apply this knowledge to other similar problems. Let's explore how easy it is to simplify and solve!
Table of Content
- Understanding the Square Root of a Fraction
- Introduction to Square Roots
- Basic Concepts of Fractions
- Simplifying Fractions: Steps and Methods
- Calculating the Square Root of a Fraction
- Mathematical Formula for Square Roots
- Step-by-Step Guide: Finding the Square Root of 4/16
- Simplifying the Fraction 4/16
- Applying Square Root to Simplified Fractions
- Visual Representation of the Process
- Examples of Square Roots of Other Fractions
- Common Mistakes and How to Avoid Them
- Real-Life Applications of Square Roots
- Advanced Topics: Square Roots of Complex Fractions
- FAQs About Square Roots and Fractions
- Conclusion and Summary
- YOUTUBE: Video này kỷ niệm Ngày Căn Bậc Hai 4/4/16 và giải thích ý nghĩa của nó một cách thú vị và dễ hiểu.
Understanding the Square Root of a Fraction
Calculating the square root of a fraction involves determining the square root of both the numerator and the denominator individually. For the fraction 4/16, the process is straightforward:
Step-by-Step Calculation
- Identify the fraction: \( \frac{4}{16} \)
- Simplify the fraction: Divide both the numerator and denominator by their greatest common divisor (GCD). Here, the GCD of 4 and 16 is 4, so: \[ \frac{4}{16} = \frac{1}{4} \]
- Apply the square root: Find the square root of the simplified fraction \( \frac{1}{4} \): \[ \sqrt{\frac{1}{4}} = \frac{\sqrt{1}}{\sqrt{4}} = \frac{1}{2} \]
General Formula
The general formula for the square root of a fraction \( \frac{a}{b} \) is given by:
\[
\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}
\]
This simplifies the process by allowing you to take the square root of the numerator and the denominator separately.
Visual Representation
Here’s a visual step-by-step guide to help understand the calculation:
Diagram showing steps to simplify and find the square root of a fraction.
More Examples
| Fraction | Simplified Form | Square Root |
|---|---|---|
| \( \frac{9}{25} \) | \( \frac{9}{25} \) | \( \frac{3}{5} \) |
| \( \frac{16}{81} \) | \( \frac{16}{81} \) | \( \frac{4}{9} \) |
| \( \frac{49}{64} \) | \( \frac{49}{64} \) | \( \frac{7}{8} \) |
Understanding these principles helps in calculating the square root of any fraction, simplifying mathematical operations.
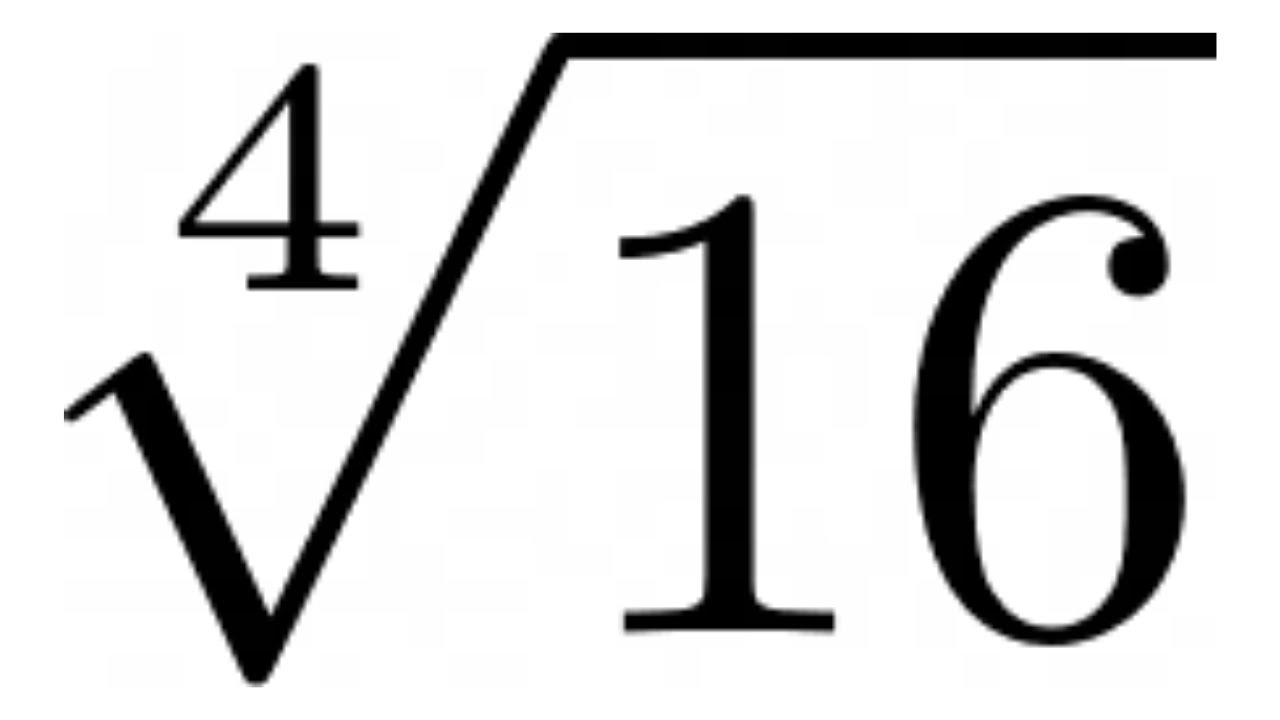
READ MORE:
Introduction to Square Roots
The concept of square roots is fundamental in mathematics, providing a basis for various applications in algebra, geometry, and beyond. A square root of a number x is a value that, when multiplied by itself, yields x. The principal square root is denoted by the symbol √, and it is always the positive root. For example, the principal square root of 9 is 3, because 32 = 9.
Square roots can be applied to whole numbers, fractions, and even complex numbers. When dealing with fractions, the process involves finding the square root of the numerator and the denominator separately.
For instance, to find the square root of the fraction 4/16:
- First, express the fraction under a single square root: √(4/16).
- Next, separate it into individual roots: √4 / √16.
- Simplify each root: √4 = 2 and √16 = 4.
- Combine the simplified values: 2 / 4, which reduces to 1 / 2.
Therefore, the square root of 4/16 is 1/2.
In general, the formula for the square root of a fraction a/b is:
$$ \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} $$
This formula simplifies the process and allows for straightforward calculation, even with more complex fractions. Understanding and calculating square roots are crucial skills in mathematics that facilitate solving quadratic equations, simplifying expressions, and performing various operations in calculus and algebra.
Basic Concepts of Fractions
Fractions are a fundamental concept in mathematics, representing parts of a whole. They are expressed as two numbers separated by a slash, such as \( \frac{a}{b} \), where \( a \) is the numerator (the part) and \( b \) is the denominator (the whole).
- Numerator and Denominator: The numerator indicates how many parts are taken, while the denominator shows the total number of equal parts in the whole. For example, in \( \frac{3}{4} \), 3 is the numerator and 4 is the denominator, meaning three out of four equal parts.
- Proper and Improper Fractions: Proper fractions have a numerator smaller than the denominator (e.g., \( \frac{3}{4} \)), while improper fractions have a numerator equal to or larger than the denominator (e.g., \( \frac{5}{3} \)). Improper fractions can also be expressed as mixed numbers.
- Equivalent Fractions: These are different fractions that represent the same value. For instance, \( \frac{1}{2} \) is equivalent to \( \frac{2}{4} \) and \( \frac{4}{8} \). To find equivalent fractions, multiply or divide both the numerator and denominator by the same number.
- Simplifying Fractions: A fraction is in its simplest form when the numerator and denominator have no common factors other than 1. For example, \( \frac{8}{12} \) simplifies to \( \frac{2}{3} \) because both 8 and 12 can be divided by 4.
- Adding and Subtracting Fractions: To add or subtract fractions, they must have a common denominator. For instance, \( \frac{1}{4} + \frac{3}{8} \) requires converting \( \frac{1}{4} \) to \( \frac{2}{8} \) so that the denominators match, resulting in \( \frac{2}{8} + \frac{3}{8} = \frac{5}{8} \).
- Multiplying and Dividing Fractions: Multiply the numerators and denominators directly. For division, multiply by the reciprocal of the divisor. For example, \( \frac{2}{3} \times \frac{4}{5} = \frac{8}{15} \) and \( \frac{2}{3} \div \frac{4}{5} = \frac{2}{3} \times \frac{5}{4} = \frac{10}{12} \) which simplifies to \( \frac{5}{6} \).
Understanding these basic concepts of fractions is essential for mastering more complex mathematical operations and real-world applications, from cooking recipes to financial calculations.
Simplifying Fractions: Steps and Methods
Simplifying fractions is an essential skill in mathematics that involves reducing the fraction to its simplest form. Here are the detailed steps and methods to simplify fractions:
- Identify the Greatest Common Divisor (GCD):
The first step in simplifying a fraction is to find the greatest common divisor (GCD) of the numerator and the denominator. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
- Divide Both Numerator and Denominator by the GCD:
Once you have identified the GCD, divide both the numerator and the denominator by this number. This step will reduce the fraction to its simplest form.
- Example of Simplifying a Fraction:
Let's simplify the fraction 4/16 using the steps above.
- Step 1: Identify the GCD of 4 and 16.
The factors of 4 are 1, 2, and 4. The factors of 16 are 1, 2, 4, 8, and 16. The GCD of 4 and 16 is 4.
- Step 2: Divide both the numerator and the denominator by the GCD (4).
\[
\frac{4 \div 4}{16 \div 4} = \frac{1}{4}
\]
Therefore, the fraction 4/16 simplifies to 1/4.
- Step 1: Identify the GCD of 4 and 16.
- Use of Prime Factorization:
Another method to simplify fractions is by using prime factorization. This involves breaking down both the numerator and the denominator into their prime factors and then canceling out the common factors.
- Example:
Simplify the fraction 4/16 using prime factorization.
Numerator (4): 2 × 2 Denominator (16): 2 × 2 × 2 × 2 Cancel out the common factors:
\[
\frac{2 \times 2}{2 \times 2 \times 2 \times 2} = \frac{1}{2 \times 2} = \frac{1}{4}
\]Thus, 4/16 simplifies to 1/4.
- Example:
- Cross Multiplication Check:
To verify if a fraction is in its simplest form, you can use cross multiplication. If the cross products are equal, the fraction is in its simplest form.
By following these steps and methods, you can simplify any fraction with confidence and accuracy.
Calculating the Square Root of a Fraction
Finding the square root of a fraction involves taking the square root of both the numerator and the denominator. This method simplifies the process and allows for straightforward calculation. Here’s a detailed step-by-step guide:
- Identify the fraction: Suppose we have the fraction \(\frac{a}{b}\).
- Square root of the numerator and denominator: Take the square root of both the numerator and the denominator separately. This is mathematically represented as: \[ \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \]
- Simplify if possible: Simplify the square roots and the resulting fraction if necessary.
Example: Calculating the Square Root of 4/16
Let's apply these steps to the fraction \(\frac{4}{16}\):
- Write the fraction: \(\frac{4}{16}\)
- Find the square root of the numerator and denominator: \[ \sqrt{\frac{4}{16}} = \frac{\sqrt{4}}{\sqrt{16}} \]
- Calculate the square roots: \[ \sqrt{4} = 2 \quad \text{and} \quad \sqrt{16} = 4 \]
- Form the new fraction: \[ \frac{\sqrt{4}}{\sqrt{16}} = \frac{2}{4} \]
- Simplify the fraction: \[ \frac{2}{4} = \frac{1}{2} \]
Therefore, the square root of \(\frac{4}{16}\) is \(\frac{1}{2}\) or 0.5.
Additional Tips
- If the fraction is not in its simplest form, simplify it before finding the square root to make calculations easier.
- If the denominator contains a square root, you may need to rationalize it by multiplying the numerator and the denominator by the same value to remove the square root from the denominator.
Practice Problem
Try finding the square root of \(\frac{9}{25}\). Follow the steps outlined above and check your answer:
- Write the fraction: \(\frac{9}{25}\)
- Find the square root of the numerator and denominator: \(\sqrt{\frac{9}{25}} = \frac{\sqrt{9}}{\sqrt{25}}\)
- Calculate the square roots: \(\sqrt{9} = 3\) and \(\sqrt{25} = 5\)
- Form the new fraction: \(\frac{3}{5}\)
The square root of \(\frac{9}{25}\) is \(\frac{3}{5}\).

Mathematical Formula for Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. The square root is denoted by the radical symbol \( \sqrt{} \). For any non-negative number \( x \), the square root is written as \( \sqrt{x} \) and satisfies the equation:
\[ y^2 = x \]
Where \( y \) is the square root of \( x \).
Here are some important properties and formulas related to square roots:
- For any positive number \( x \), there are two square roots: one positive and one negative. They can be written as \( \pm \sqrt{x} \).
- The principal (non-negative) square root of \( x \) is denoted by \( \sqrt{x} \).
- If \( x \) is a perfect square (like 1, 4, 9, 16, etc.), then \( \sqrt{x} \) is an integer.
- For any real number \( x \), the square root can also be expressed using exponent notation: \( x^{1/2} \).
Examples:
- To find the square root of 144:
\[ \sqrt{144} = 12 \]
- To find the square root of 60:
\[ \sqrt{60} = \sqrt{4 \times 15} = 2\sqrt{15} \]
- To find the length of the side of a square with an area of 400 square units:
\[ \text{Side length} = \sqrt{400} = 20 \text{ units} \]
The square root formula has various applications in algebra, geometry, and other fields of mathematics. It is essential in solving quadratic equations, computing areas and volumes, and understanding physical laws.
For negative numbers, the square roots involve imaginary numbers. The square root of a negative number \( -x \) is written as \( i\sqrt{x} \), where \( i \) is the imaginary unit representing \( \sqrt{-1} \).
In summary, the square root formula can be expressed as:
\[ \sqrt{x} = x^{1/2} \]
Step-by-Step Guide: Finding the Square Root of 4/16
Finding the square root of a fraction involves a few simple steps. Below, we will guide you through the process using the fraction \( \frac{4}{16} \).
-
Identify the Numerator and Denominator:
In the fraction \( \frac{4}{16} \), the numerator is 4 and the denominator is 16.
-
Simplify the Fraction (if necessary):
Before finding the square root, it is often easier to simplify the fraction. \( \frac{4}{16} \) can be simplified to \( \frac{1}{4} \).
This is done by dividing both the numerator and the denominator by their greatest common divisor (GCD), which is 4 in this case.
\[
\frac{4 \div 4}{16 \div 4} = \frac{1}{4}
\] -
Apply the Square Root to the Numerator and Denominator:
Next, apply the square root to both the numerator and the denominator separately.
\[
\sqrt{\frac{1}{4}} = \frac{\sqrt{1}}{\sqrt{4}}
\]\[
\sqrt{1} = 1 \quad \text{and} \quad \sqrt{4} = 2
\] -
Combine the Results:
After finding the square roots of the numerator and the denominator, combine them to get the final result.
\[
\sqrt{\frac{1}{4}} = \frac{1}{2}
\] -
Verify the Result:
Finally, it's always good practice to verify the result by squaring it back to check if you get the original fraction.
\[
\left( \frac{1}{2} \right)^2 = \frac{1^2}{2^2} = \frac{1}{4}
\]As expected, squaring \( \frac{1}{2} \) gives us back \( \frac{1}{4} \), confirming our result is correct.
Therefore, the square root of \( \frac{4}{16} \) is \( \frac{1}{2} \).
Simplifying the Fraction 4/16
To simplify the fraction \( \frac{4}{16} \), follow these steps:
-
Find the Greatest Common Divisor (GCD) of the numerator and the denominator. The GCD of 4 and 16 is 4.
-
Divide both the numerator and the denominator by the GCD.
\[
\frac{4}{16} = \frac{4 \div 4}{16 \div 4} = \frac{1}{4}
\]
Thus, the fraction \( \frac{4}{16} \) simplifies to \( \frac{1}{4} \).
Alternative Method: Using Prime Factorization
Prime factorization involves breaking down both the numerator and the denominator into their prime factors.
- Prime factors of 4: \( 2 \times 2 \)
- Prime factors of 16: \( 2 \times 2 \times 2 \times 2 \)
Rewrite the fraction using these prime factors:
\[
\frac{4}{16} = \frac{2 \times 2}{2 \times 2 \times 2 \times 2}
\]
Cancel out the common factors:
\[
\frac{2 \times 2}{2 \times 2 \times 2 \times 2} = \frac{1}{2 \times 2} = \frac{1}{4}
\]
Therefore, using prime factorization, we also get the simplified fraction \( \frac{1}{4} \).
Method Summary
Both methods show that simplifying the fraction \( \frac{4}{16} \) results in \( \frac{1}{4} \).
Applying Square Root to Simplified Fractions
When you apply the square root to a simplified fraction, the process becomes straightforward by taking the square root of both the numerator and the denominator separately. Here's a step-by-step guide:
Start with the simplified fraction. For example, consider the fraction \( \frac{1}{4} \).
Take the square root of the numerator and the denominator separately:
\[
\sqrt{\frac{1}{4}} = \frac{\sqrt{1}}{\sqrt{4}}
\]Simplify the square roots:
\[
\frac{\sqrt{1}}{\sqrt{4}} = \frac{1}{2}
\]Therefore, the square root of \( \frac{1}{4} \) is \( \frac{1}{2} \).
Let's look at another example:
Consider the fraction \( \frac{9}{16} \).
Take the square root of the numerator and the denominator separately:
\[
\sqrt{\frac{9}{16}} = \frac{\sqrt{9}}{\sqrt{16}}
\]Simplify the square roots:
\[
\frac{\sqrt{9}}{\sqrt{16}} = \frac{3}{4}
\]Therefore, the square root of \( \frac{9}{16} \) is \( \frac{3}{4} \).
For fractions that do not simplify to a perfect square, you may end up with an irrational number. For example, consider the fraction \( \frac{2}{3} \):
Take the square root of the numerator and the denominator separately:
\[
\sqrt{\frac{2}{3}} = \frac{\sqrt{2}}{\sqrt{3}}
\]To rationalize the denominator, multiply both the numerator and the denominator by \( \sqrt{3} \):
\[
\frac{\sqrt{2}}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{\sqrt{6}}{3}
\]Therefore, the square root of \( \frac{2}{3} \) is \( \frac{\sqrt{6}}{3} \), which is an irrational number.
By following these steps, you can simplify and find the square root of any fraction, whether it results in a rational or irrational number.

Visual Representation of the Process
Visualizing the process of finding the square root of a fraction can greatly aid in understanding. Here, we will break down the square root of step by step with visual aids.
Step 1: Simplifying the Fraction
First, we simplify the fraction . This can be represented visually as:
- Original fraction:
- Simplified fraction: (after dividing both numerator and denominator by 4)
In visual terms, can be represented as 4 parts of a whole divided into 16 sections:

After simplification, it becomes 1 part of a whole divided into 4 sections:

Step 2: Applying the Square Root
Next, we apply the square root to the simplified fraction :
- Square root of numerator: = 1
- Square root of denominator: = 2
Therefore, the square root of is .
This can be visually represented as:

Combining the Steps
To summarize, the visual process of finding the square root of involves:
- Simplifying to
- Taking the square root of to get
This visual approach helps in understanding the process clearly and effectively.
Examples of Square Roots of Other Fractions
Understanding the square root of fractions can be made easier by looking at various examples. Below, we explore some common fractions and their square roots, demonstrating the steps involved in simplifying and solving these fractions.
-
Example 1: Square Root of 9/16
- Start with the fraction: \( \frac{9}{16} \).
- Find the square root of the numerator and the denominator separately: \[ \sqrt{9} = 3 \quad \text{and} \quad \sqrt{16} = 4 \]
- Combine the results to find the square root of the fraction: \[ \sqrt{\frac{9}{16}} = \frac{3}{4} \]
-
Example 2: Square Root of 1/25
- Start with the fraction: \( \frac{1}{25} \).
- Find the square root of the numerator and the denominator separately: \[ \sqrt{1} = 1 \quad \text{and} \quad \sqrt{25} = 5 \]
- Combine the results to find the square root of the fraction: \[ \sqrt{\frac{1}{25}} = \frac{1}{5} \]
-
Example 3: Square Root of 4/9
- Start with the fraction: \( \frac{4}{9} \).
- Find the square root of the numerator and the denominator separately: \[ \sqrt{4} = 2 \quad \text{and} \quad \sqrt{9} = 3 \]
- Combine the results to find the square root of the fraction: \[ \sqrt{\frac{4}{9}} = \frac{2}{3} \]
-
Example 4: Square Root of 25/36
- Start with the fraction: \( \frac{25}{36} \).
- Find the square root of the numerator and the denominator separately: \[ \sqrt{25} = 5 \quad \text{and} \quad \sqrt{36} = 6 \]
- Combine the results to find the square root of the fraction: \[ \sqrt{\frac{25}{36}} = \frac{5}{6} \]
-
Example 5: Square Root of 16/81
- Start with the fraction: \( \frac{16}{81} \).
- Find the square root of the numerator and the denominator separately: \[ \sqrt{16} = 4 \quad \text{and} \quad \sqrt{81} = 9 \]
- Combine the results to find the square root of the fraction: \[ \sqrt{\frac{16}{81}} = \frac{4}{9} \]
These examples illustrate the process of finding the square root of fractions by simplifying the numerator and the denominator separately. This method can be applied to any fraction to determine its square root.
Common Mistakes and How to Avoid Them
When dealing with square roots of fractions, it's easy to make mistakes. Here are some common errors and tips on how to avoid them:
- Mistake 1: Incorrect Simplification
Some students incorrectly simplify the square root of a sum as the sum of the square roots. Remember, \(\sqrt{a + b} \ne \sqrt{a} + \sqrt{b}\). For example, \(\sqrt{4 + 9} \ne \sqrt{4} + \sqrt{9}\).
- Mistake 2: Forgetting to Simplify the Fraction First
Always simplify the fraction before applying the square root. For instance, instead of finding \(\sqrt{\frac{4}{16}}\) directly, simplify it to \(\sqrt{\frac{1}{4}}\) first.
- Mistake 3: Ignoring Rationalization of the Denominator
Ensure the denominator is rationalized. For example, for \(\frac{1}{\sqrt{2}}\), multiply by \(\frac{\sqrt{2}}{\sqrt{2}}\) to get \(\frac{\sqrt{2}}{2}\).
- Mistake 4: Incorrectly Canceling Terms
Do not cancel terms incorrectly. For instance, \(\frac{\sqrt{4}}{\sqrt{16}} = \frac{2}{4} = \frac{1}{2}\), but do not cancel square roots incorrectly across addition or subtraction.
- Mistake 5: Misapplying the Square Root Property
Use the property \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\) correctly. This helps to simplify square root fractions accurately.
By understanding and avoiding these common mistakes, you can ensure accuracy in simplifying square root fractions and improve your mathematical skills.
Real-Life Applications of Square Roots
Square roots are used in various real-life scenarios to solve practical problems. Here are some detailed examples:
-
Architecture and Construction:
Square roots are essential in determining the dimensions and area of different structures. For example, if the area of a square plot is known, the side length can be found by taking the square root of the area. This helps in accurate planning and construction.
-
Physics and Engineering:
Square roots play a critical role in formulas such as calculating the period of a pendulum, where the period is proportional to the square root of the length of the pendulum. In engineering, square roots are used in stress analysis and in determining material properties.
-
Finance:
In finance, square roots are used to calculate the standard deviation of investment returns, which is a measure of risk. The square root of the variance gives the standard deviation, helping investors to understand the volatility of their investments.
-
Medicine:
Square roots are used in dosages calculations in medicine, particularly in adjusting doses based on body surface area. For example, the square root of the height multiplied by the weight (in specific units) helps determine the appropriate dose for patients.
-
Astronomy:
In astronomy, square roots are used to calculate the luminosity of stars. The inverse square law, which relates the brightness of a star to its distance from the observer, involves square root calculations to determine the actual brightness and distance.
-
Geology:
Geologists use square roots to calculate the intensity of earthquakes. The magnitude of an earthquake is often related to the logarithm of the amplitude of seismic waves, and square root calculations help in determining the energy released.
These examples illustrate the importance of understanding square roots and their applications in various fields. Mastery of this concept can lead to better problem-solving skills in everyday life and professional activities.
Advanced Topics: Square Roots of Complex Fractions
In this section, we will explore more advanced concepts related to finding the square roots of complex fractions. This involves fractions that may include irrational numbers, larger numerators and denominators, and additional operations within the square root. Let's delve into these topics with a step-by-step approach.
Square Roots of Fractions with Irrational Numbers
When dealing with fractions that contain irrational numbers, the process of finding the square root remains similar but requires careful handling of the irrational parts.
Consider the fraction \( \frac{\sqrt{2}}{4} \).
- Simplify the fraction if possible: \( \frac{\sqrt{2}}{4} \) is already in its simplest form.
- Apply the square root: \( \sqrt{\frac{\sqrt{2}}{4}} \).
- Separate the square root: \( \frac{\sqrt{\sqrt{2}}}{\sqrt{4}} \).
- Simplify each part: \( \frac{\sqrt[4]{2}}{2} \).
Thus, the square root of \( \frac{\sqrt{2}}{4} \) is \( \frac{\sqrt[4]{2}}{2} \).
Square Roots of Larger Fractions
For larger fractions, the process involves the same fundamental steps but can require more simplification.
Consider the fraction \( \frac{49}{81} \).
- Simplify the fraction if needed: \( \frac{49}{81} \) is already in its simplest form.
- Apply the square root: \( \sqrt{\frac{49}{81}} \).
- Separate the square root: \( \frac{\sqrt{49}}{\sqrt{81}} \).
- Simplify each part: \( \frac{7}{9} \).
Thus, the square root of \( \frac{49}{81} \) is \( \frac{7}{9} \).
Combining Operations with Square Roots
Sometimes, fractions under a square root may involve additional operations such as addition or subtraction within the numerator or denominator.
Consider the fraction \( \frac{1 + \sqrt{3}}{2} \).
- Apply the square root: \( \sqrt{\frac{1 + \sqrt{3}}{2}} \).
- Separate the square root: \( \frac{\sqrt{1 + \sqrt{3}}}{\sqrt{2}} \).
- While this expression cannot be simplified further, it can be left in this form for practical use.
Table of Common Square Roots of Fractions
| Fraction | Square Root |
|---|---|
| \( \frac{1}{4} \) | \( \frac{1}{2} \) |
| \( \frac{9}{16} \) | \( \frac{3}{4} \) |
| \( \frac{25}{36} \) | \( \frac{5}{6} \) |
| \( \frac{1}{9} \) | \( \frac{1}{3} \) |
| \( \frac{49}{64} \) | \( \frac{7}{8} \) |
Conclusion
Understanding how to find the square roots of complex fractions involves mastering the basic steps and then applying them to more intricate cases. Whether dealing with irrational numbers, larger fractions, or additional operations, the principles remain consistent, allowing for accurate and efficient calculations.
FAQs About Square Roots and Fractions
This section addresses common questions regarding the calculation and understanding of square roots and fractions. The explanations provided will help you navigate through these mathematical concepts with ease.
1. How do you find the square root of a fraction?
To find the square root of a fraction, you need to take the square root of both the numerator and the denominator separately.
For example, to find the square root of \( \frac{4}{16} \):
- Find the square root of the numerator: \( \sqrt{4} = 2 \).
- Find the square root of the denominator: \( \sqrt{16} = 4 \).
- Write the fraction with these square roots: \( \frac{2}{4} \).
- Simplify the fraction if possible: \( \frac{2}{4} = \frac{1}{2} \).
Thus, \( \sqrt{\frac{4}{16}} = \frac{1}{2} \).
2. Can you simplify a fraction before finding its square root?
Yes, simplifying a fraction before finding its square root can often make the calculation easier. For instance, with \( \frac{4}{16} \):
- Simplify \( \frac{4}{16} \) to \( \frac{1}{4} \).
- Then find the square root: \( \sqrt{\frac{1}{4}} = \frac{\sqrt{1}}{\sqrt{4}} = \frac{1}{2} \).
3. What if the fraction has an irrational number?
When a fraction involves irrational numbers, the approach remains the same but requires handling the irrational part carefully. For example, \( \sqrt{\frac{\sqrt{2}}{4}} \):
- Separate the square roots: \( \frac{\sqrt{\sqrt{2}}}{\sqrt{4}} \).
- Simplify each part: \( \frac{\sqrt[4]{2}}{2} \).
4. How do you handle square roots of fractions with complex numerators or denominators?
For more complex fractions, such as \( \frac{1 + \sqrt{3}}{2} \), you can apply the square root to the entire fraction:
- Apply the square root: \( \sqrt{\frac{1 + \sqrt{3}}{2}} \).
- Separate the square root: \( \frac{\sqrt{1 + \sqrt{3}}}{\sqrt{2}} \).
- Sometimes, the expression can be left in this form if further simplification is not possible.
5. Why can we separate the square root of a fraction?
The square root of a fraction can be separated into the square roots of the numerator and the denominator because of the properties of exponents and the inverse relationship between squaring and square roots. Mathematically, \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \).
6. Are there any common mistakes to avoid?
Some common mistakes include:
- Not simplifying the fraction before taking the square root.
- Forgetting to rationalize the denominator if it remains an irrational number.
- Incorrectly applying the square root to only one part of the fraction.
7. Can all fractions be simplified after finding the square root?
No, not all fractions can be simplified after finding the square root. For example, \( \sqrt{\frac{2}{5}} \) remains \( \frac{\sqrt{2}}{\sqrt{5}} \) and may require rationalization if needed.
Conclusion
Understanding the square roots of fractions involves recognizing the properties of square roots and fractions. By carefully applying these principles, you can accurately compute the square roots and simplify the results as needed.
Conclusion and Summary
Understanding the square root of fractions is an essential skill in mathematics, allowing for the simplification and manipulation of expressions involving ratios. In this guide, we have explored various methods and principles related to calculating and simplifying the square root of fractions, with specific focus on the example \( \frac{4}{16} \).
Key Points Covered
- Basic Principles: The square root of a fraction can be found by taking the square root of the numerator and the square root of the denominator separately. This is represented as \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \).
- Example: For \( \frac{4}{16} \), the square roots of the numerator and the denominator are \( \sqrt{4} = 2 \) and \( \sqrt{16} = 4 \) respectively, resulting in \( \frac{2}{4} \), which simplifies to \( \frac{1}{2} \).
- Simplifying Fractions: Simplifying fractions before or after taking the square root can make calculations easier. In the case of \( \frac{4}{16} \), simplifying to \( \frac{1}{4} \) first gives the same result \( \frac{1}{2} \).
- Complex Fractions: For fractions involving irrational numbers or additional operations, such as \( \frac{\sqrt{2}}{4} \) or \( \frac{1 + \sqrt{3}}{2} \), the same principles apply, but care must be taken to handle the irrational parts appropriately.
Steps for Calculating Square Roots of Fractions
- Identify and simplify the fraction if possible.
- Take the square root of the numerator and the denominator separately.
- Simplify the resulting fraction if needed.
- Ensure the denominator is rationalized if it contains an irrational number.
Examples and Applications
| Fraction | Square Root |
|---|---|
| \( \frac{1}{4} \) | \( \frac{1}{2} \) |
| \( \frac{9}{16} \) | \( \frac{3}{4} \) |
| \( \frac{25}{36} \) | \( \frac{5}{6} \) |
| \( \frac{49}{64} \) | \( \frac{7}{8} \) |
Final Thoughts
The process of finding and simplifying the square root of a fraction combines fundamental arithmetic with an understanding of square roots and rationalization techniques. By mastering these concepts, you can efficiently handle a wide range of mathematical problems involving fractions and square roots. Always remember to simplify where possible and ensure your final answer is in its simplest form.
READ MORE:
Video này kỷ niệm Ngày Căn Bậc Hai 4/4/16 và giải thích ý nghĩa của nó một cách thú vị và dễ hiểu.
Ngày Căn Bậc Hai 4/4/16