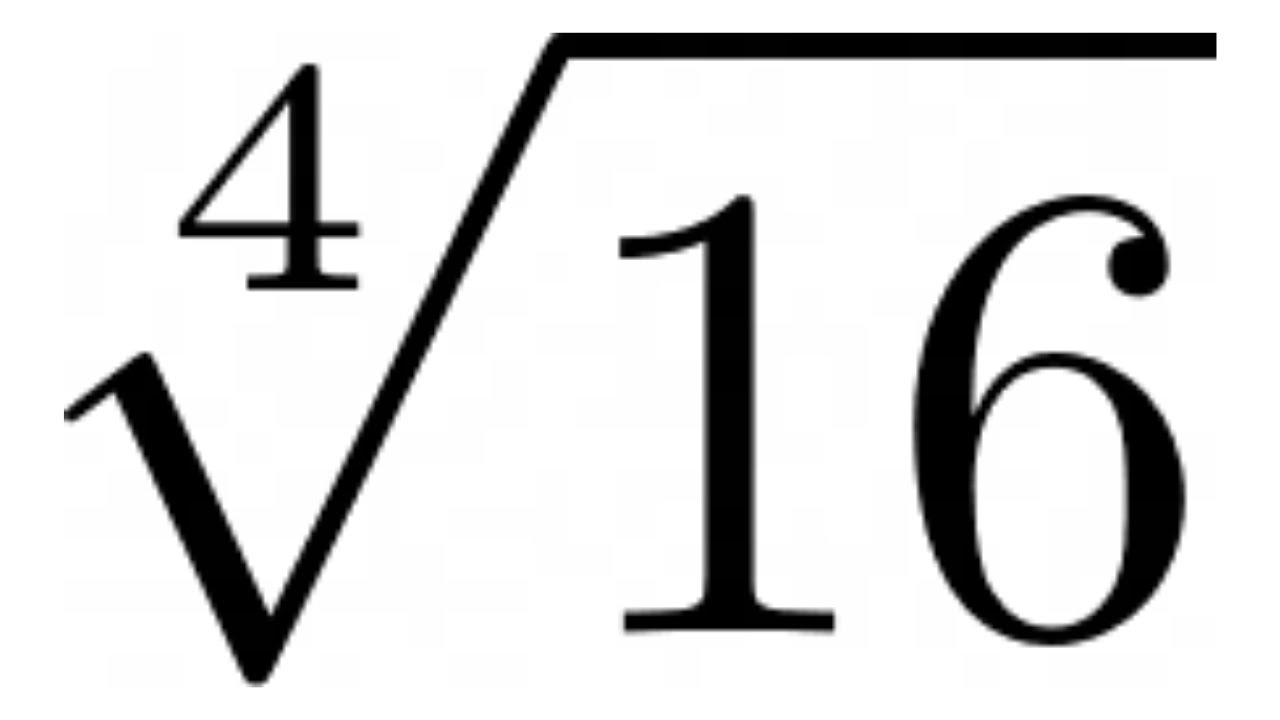Topic square root of 162: Unlock the mysteries of mathematics by exploring the square root of 162. This intriguing number, approximately 12.7279, offers a gateway to understanding irrational numbers and their properties. Dive into various methods for calculating and simplifying square roots, and discover practical applications in everyday life and advanced math concepts.
Table of Content
- Square Root of 162
- Introduction
- Definition of Square Root
- Properties of Square Root of 162
- Methods to Calculate Square Root
- Exact and Decimal Forms
- Rational vs. Irrational Numbers
- Simplifying Square Roots
- Applications of Square Root of 162
- Examples and Exercises
- FAQs
- Conclusion
- YOUTUBE: Khám phá cách giải một vấn đề căn bậc hai phức tạp trong video này. Học cách giải phương trình với √162 và các kỹ thuật toán học khác.
Square Root of 162
The square root of 162 can be expressed in multiple forms, and it is a number that appears in various mathematical contexts. Below is a detailed explanation of how to find and understand the square root of 162.
Calculation
The square root of 162 is not a perfect square, and it is an irrational number. The simplest form of the square root of 162 can be found by factoring:
Thus, the exact form is \( 9\sqrt{2} \). In decimal form, it is approximately:
Steps to Calculate
- Factor 162 into its prime factors: \( 162 = 81 \times 2 \).
- Rewrite the square root as the product of square roots: \( \sqrt{162} = \sqrt{81 \times 2} \).
- Simplify \( \sqrt{81} \) to 9, giving \( 9\sqrt{2} \).
Methods
- Prime Factorization: By breaking down 162 into \( 81 \times 2 \), we can easily find its square root.
- Long Division Method: This method can be used to find a more precise decimal value for the square root of 162, resulting in approximately 12.727.
Properties
- The number 162 is not a perfect square, which means its square root is an irrational number.
- The square root of 162 in radical form is \( 9\sqrt{2} \).
- As a decimal, it is approximately 12.727922061.
Applications
Understanding the square root of 162 is useful in various mathematical problems and real-world applications, including geometry, physics, and engineering.
Examples
- Example 1: Finding the square root using the prime factorization method yields \( 9\sqrt{2} \).
- Example 2: Using the long division method gives a more precise decimal value of approximately 12.727.

READ MORE:
Introduction
The square root of 162 is an important mathematical concept, often encountered in various fields such as algebra, geometry, and even practical applications. The square root, denoted as √162, is the number that, when multiplied by itself, equals 162. This number is approximately 12.72792206, which can also be represented in various forms including decimal and radical forms.
In this article, we will explore the methods to calculate the square root of 162, understand its properties, and delve into its practical applications.
- Definition and Properties of Square Root
- Methods to Calculate the Square Root of 162
- Prime Factorization
- Long Division Method
- Practical Applications of Square Root of 162
Definition of Square Root
The square root of a number is a value that, when multiplied by itself, gives the original number. In mathematical terms, the square root of a number \( n \) is denoted as \( \sqrt{n} \). For instance, the square root of 162 can be represented as \( \sqrt{162} \). The process of finding the square root involves determining a number which, when squared, results in the original number.
The square root of 162 is not a perfect square, meaning it cannot be expressed as the product of an integer by itself. Instead, it is an irrational number, which implies that it has a non-repeating, non-terminating decimal expansion. The exact form of the square root of 162 is:
\[ \sqrt{162} = 12.7279220614 \]
This can also be expressed in exponential form as \( 162^{1/2} \) or in radical form as \( \sqrt{162} \).
There are several methods to find the square root of a number, including estimation and trial-and-error, the long division method, and Newton's method (iterative approximation). Each method involves different steps and levels of precision.
Methods to Find the Square Root of 162
- Estimation and Trial-and-Error: By finding two perfect squares between which 162 lies (144 and 169, or \( 12^2 \) and \( 13^2 \)), we can estimate that \( \sqrt{162} \) is between 12 and 13. Testing values like 12.5, 12.6, and so on, we can approximate \( \sqrt{162} \) to 12.727.
- Long Division Method: This method involves setting up a long division problem with 162.000000 and finding the square root digit by digit. This precise method helps in calculating the square root to the desired number of decimal places.
- Newton’s Method (Iterative): Starting with an initial guess close to the square root, for example, 12, the iterative formula \( x_{n+1} = \frac{1}{2} ( x_n + \frac{162}{x_n} ) \) is used to refine the estimate until the desired precision is achieved.
Understanding the concept of square roots and the methods to find them is fundamental in various mathematical applications and analysis.
Properties of Square Root of 162
The square root of 162 has several interesting properties. Below, we explore these properties step-by-step to understand this value better.
- Exact Form: The square root of 162 can be expressed in its simplest radical form as \( \sqrt{162} = 9\sqrt{2} \).
- Decimal Form: The decimal approximation of the square root of 162 is approximately 12.7279.
- Simplification: The simplification process involves breaking down 162 into its prime factors. 162 can be factored as \( 162 = 81 \times 2 \), where 81 is a perfect square. Therefore, \( \sqrt{162} = \sqrt{81 \times 2} = \sqrt{81} \times \sqrt{2} = 9\sqrt{2} \).
- Principal Square Root: The principal square root of 162 is the positive value \( 12.7279 \).
- Negative Square Root: The negative square root of 162 is \( -12.7279 \).
- Applications:
- Geometry: In geometry, the square root of 162 might be used to determine the length of the diagonal of a square with an area of 162 square units.
- Algebra: In algebra, understanding how to simplify \( \sqrt{162} \) helps in solving quadratic equations and other higher-order polynomials.
- Root Properties:
- The product of square roots property: \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \).
- The power property: \( \sqrt{x} = x^{1/2} \).
Understanding the properties of the square root of 162 allows for better comprehension in various mathematical contexts, ensuring a solid grasp of both basic and advanced concepts.
Methods to Calculate Square Root
There are several methods to calculate the square root of a number, including estimation, trial-and-error, the long division method, and Newton's method. Here, we will detail each method step by step using the square root of 162 as an example.
- Estimation and Trial-and-Error
- Estimate: Since 162 is between 144 (12²) and 169 (13²), the square root is between 12 and 13.
- Trial-and-Error: Test values between 12 and 13 to refine the estimate.
- 12.5² = 156.25 (too low)
- 12.6² = 158.76 (too low)
- 12.7² = 161.29 (very close)
- 12.8² = 163.84 (too high)
- Conclusion: The square root of 162 is approximately 12.7.
- Long Division Method
- Set up long division: Start with 162.000000.
- Find the square root digit by digit.
- Pair the digits from right to left: 1 | 62 | 00 | 00.
- The largest square less than or equal to 1 is 1, so write 1 above the line.
- Subtract 1 from 1, bring down the next pair (62), and double the quotient (1 × 2 = 2).
- Find the next digit which, when added to 20 and multiplied by itself, gives a product less than or equal to 62. Here, it is 2 (2 × 22 = 44).
- Repeat this process to get more digits of the square root.
- Newton’s Method (Iterative)
- Initial Guess: Start with a guess close to the actual value, for example, 12.
- Iterative Calculation: Use the formula \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{162}{x_n} \right) \).
- Repeat until the desired precision is achieved.
- Example:
- Initial guess \( x_0 = 12 \)
- \( x_1 = \frac{1}{2} \left( 12 + \frac{162}{12} \right) = 12.25 \)
- \( x_2 = \frac{1}{2} \left( 12.25 + \frac{162}{12.25} \right) \approx 12.727 \)
Using these methods, we find that the square root of 162 is approximately 12.727. Each method offers a different approach, providing flexibility depending on the tools and precision required.

Exact and Decimal Forms
The square root of 162 can be expressed in both exact and decimal forms. The exact form of the square root of 162 is given by:
\(\sqrt{162} = \sqrt{81 \times 2} = 9\sqrt{2}\)
This exact form simplifies the square root by factoring out the largest perfect square, 81, which is a factor of 162. Therefore, the exact form is \(9\sqrt{2}\).
When expressed as a decimal, the square root of 162 is approximately:
\(\sqrt{162} \approx 12.7279\)
This decimal form is derived using methods such as long division or iterative approaches like Newton's method.
- Long Division Method: This method involves dividing the number in pairs of digits and finding the root digit by digit, resulting in a precise decimal value.
- Newton's Method: An iterative approach where an initial guess is refined repeatedly using the formula \(x_{n+1} = \frac{1}{2}(x_n + \frac{162}{x_n})\) until the desired precision is achieved.
The square root of 162, therefore, highlights the interplay between its exact radical form and its practical decimal approximation, demonstrating both mathematical precision and usability in real-world calculations.
Rational vs. Irrational Numbers
Understanding the difference between rational and irrational numbers is fundamental in mathematics. Let's explore their definitions and characteristics, and specifically analyze the nature of the square root of 162.
- Rational Numbers:
- These numbers can be expressed as a fraction where both the numerator and denominator are integers.
- The denominator is not zero.
- Examples include integers, fractions, and terminating or repeating decimals.
- Irrational Numbers:
- These numbers cannot be written as a simple fraction.
- Their decimal expansions are non-terminating and non-repeating.
- Examples include π (pi) and the square root of non-perfect squares like √2.
The square root of 162 is approximately 12.7279220614. This decimal does not terminate or repeat, thus categorizing it as an irrational number. Here's a step-by-step breakdown of why:
| Expression | Explanation |
| √162 | The value which, when multiplied by itself, equals 162. |
| Approx. 12.7279220614 | This value is a non-terminating, non-repeating decimal, confirming its irrationality. |
Thus, while rational numbers include easily expressible fractions and repeating decimals, irrational numbers like the square root of 162 demonstrate the complex and non-repetitive nature of certain mathematical values.
Simplifying Square Roots
To simplify the square root of a number, we look for perfect square factors. Let's simplify the square root of 162 step by step:
-
First, find the prime factorization of 162:
162 can be divided by 2:
\(162 \div 2 = 81\)
81 is a perfect square and can be further factored:
\(81 = 9 \times 9\)
Therefore, \(162 = 2 \times 9 \times 9\)
-
Rewrite 9 as \(3 \times 3\):
\(162 = 2 \times 3 \times 3 \times 3 \times 3\)
-
Group the pairs of prime factors:
\(162 = (3 \times 3) \times (3 \times 3) \times 2\)
-
Take the square root of each pair:
\(\sqrt{162} = \sqrt{(3 \times 3) \times (3 \times 3) \times 2}\)
\(\sqrt{162} = \sqrt{3^2 \times 3^2 \times 2}\)
Since the square root of \(3^2\) is 3, we can simplify:
\(\sqrt{3^2} = 3\)
-
Combine the results:
\(\sqrt{162} = 3 \times 3 \times \sqrt{2}\)
\(\sqrt{162} = 9 \sqrt{2}\)
Therefore, the simplified form of the square root of 162 is \(9 \sqrt{2}\).
| Step | Description | Result |
|---|---|---|
| 1 | Prime factorization | \(162 = 2 \times 3 \times 3 \times 3 \times 3\) |
| 2 | Group pairs | \(162 = (3 \times 3) \times (3 \times 3) \times 2\) |
| 3 | Simplify square roots | \(\sqrt{162} = 9 \sqrt{2}\) |
In summary, to simplify the square root of 162:
- Factor the number into prime factors.
- Group the prime factors into pairs.
- Simplify the square root of each pair.
- Combine the simplified results.
Using these steps, we find that the square root of 162 simplifies to \(9 \sqrt{2}\).
Applications of Square Root of 162
The square root of 162, approximately 12.727, has various practical applications across different fields. Here are some significant areas where this mathematical concept is used:
-
Geometry:
Square roots are essential in geometry for calculating the lengths of sides in right triangles using the Pythagorean theorem. For example, if the area of a square is 162 square units, the length of one side is \( \sqrt{162} \) units, which is approximately 12.727 units.
-
Algebra:
In algebra, square roots are often used to solve quadratic equations. If \( x^2 = 162 \), then \( x = \pm \sqrt{162} \). This helps in finding the roots of equations and understanding the behavior of quadratic functions.
-
Physics and Engineering:
Square roots are utilized in various physics formulas, such as those calculating speed, acceleration, and force. For instance, the time \( t \) it takes for an object to fall from a height \( h \) is given by \( t = \sqrt{2h/g} \). If an object is dropped from 162 feet, the time to reach the ground is approximately \( \sqrt{2 \times 162 / 32.2} \approx 3.17 \) seconds.
-
Statistics and Probability:
The square root is crucial in statistics, particularly in the calculation of the standard deviation, which is the square root of the variance. This measure helps in understanding the spread of data points in a dataset.
-
Computer Science:
In computer science, algorithms for calculating distances between points, such as the Euclidean distance in graphics and machine learning, often use the square root function. For example, the distance between two points (x1, y1) and (x2, y2) is \( \sqrt{(x2 - x1)^2 + (y2 - y1)^2} \).
-
Finance:
Square roots are used in financial models to calculate compound interest and assess risk and return. For instance, the annualized return of an investment can be found using the geometric mean, which involves taking the square root of the product of the returns.
Understanding and applying the square root of 162 in these various contexts showcases its importance in both theoretical and practical scenarios, highlighting its utility across different domains.

Examples and Exercises
In this section, we will explore examples and exercises to understand the square root of 162 better.
Example 1: Finding the Square Root of 162 Using Prime Factorization
Prime factorization involves breaking down 162 into its prime factors:
\[ 162 = 2 \times 3^4 \]
Therefore, the square root is:
\[ \sqrt{162} = \sqrt{2 \times 3^4} = 3^2 \times \sqrt{2} = 9\sqrt{2} \approx 12.727 \]
Example 2: Long Division Method
The long division method helps in finding more precise values of square roots:
Step-by-step, the square root of 162 calculated using long division is approximately 12.727.
Exercise 1: Calculate the Square Root of 162 Using the Repeated Subtraction Method
The repeated subtraction method is not suitable for finding the square root of 162 as it is not a perfect square.
Exercise 2: Rational vs. Irrational Numbers
Show that \(\sqrt{162}\) is irrational by expressing it in its simplest radical form:
\[ \sqrt{162} = \sqrt{81 \times 2} = 9\sqrt{2} \]
Since \(\sqrt{2}\) is irrational, \(\sqrt{162}\) is also irrational.
Exercise 3: Applications
Use the value of \(\sqrt{162}\) in practical problems:
- If a square garden has an area of 162 square meters, find the side length of the garden.
- Given that \(\sqrt{162} \approx 12.727\), the side length of the garden is approximately 12.727 meters.
Solution: The side length is \(\sqrt{162}\) meters.
Practice Problems
- Simplify \(\sqrt{50 \times 2^3}\).
- Verify that \(\sqrt{162}\) is irrational.
- Use the long division method to find \(\sqrt{162}\) up to two decimal places.
- Calculate the area of a square with side length \(\sqrt{162}\) meters.
Answers to Practice Problems
- \[ \sqrt{50 \times 2^3} = \sqrt{400} = 20 \]
- Since 162 = 2 \times 81 and 81 is a perfect square, simplifying \(\sqrt{162}\) results in \(9\sqrt{2}\). As \(\sqrt{2}\) is irrational, \(\sqrt{162}\) is irrational.
- Using the long division method, \(\sqrt{162} \approx 12.73\).
- The area is \(\sqrt{162}^2 = 162\) square meters.
FAQs
Here are some frequently asked questions about the square root of 162:
What is the Square Root of 162?
The square root of 162 is approximately 12.7279220614, often rounded to 12.73 for simplicity.
Is the Square Root of 162 Rational or Irrational?
The square root of 162 is an irrational number. This is because its decimal representation is non-terminating and non-repeating.
What is the Simplified Form of the Square Root of 162?
The simplified form of the square root of 162 is \( 9\sqrt{2} \). This simplification uses the factorization \( 162 = 81 \times 2 \).
How is the Square Root of 162 Calculated?
The square root of 162 can be calculated using several methods:
- Prime Factorization: Break down 162 into prime factors: \( 162 = 2 \times 3^4 \). Then, \( \sqrt{162} = \sqrt{2 \times 3^4} = 3^2 \times \sqrt{2} = 9\sqrt{2} \).
- Long Division Method: This involves dividing 162 step by step to find the square root to the desired precision.
- Calculator: Simply input 162 and use the square root function to get the result \( \approx 12.7279 \).
What are the Applications of the Square Root of 162?
The square root of 162 is used in various mathematical computations, especially in geometry and algebra, such as calculating the diagonal of a square or solving quadratic equations.
Is 162 a Perfect Square?
No, 162 is not a perfect square. A perfect square is a number that can be expressed as the square of an integer, and 162 does not meet this criterion.
What is the Cube Root of 162?
The cube root of 162 is approximately 5.451, found using the cube root function.
What is the Fourth Root of 162?
The fourth root of 162 is approximately 3.0723, calculated by taking the fourth root of the number.
Can the Square Root of 162 be Written as a Fraction?
As an irrational number, the square root of 162 cannot be expressed as an exact fraction. However, it can be approximated by fractions, such as \( \frac{1273}{100} \).
Conclusion
The square root of 162, approximately equal to 12.727, is an important mathematical concept with diverse applications in various fields such as geometry, algebra, and real-world problem-solving. Understanding how to simplify and compute square roots enhances one's mathematical skills and provides a foundation for more advanced topics.
Key points to remember include:
- Mathematical Importance: The square root of 162 is used in solving quadratic equations and understanding the properties of numbers.
- Methods of Calculation: There are several methods to find the square root, including prime factorization and the long division method. These methods provide exact and approximate values, respectively.
- Applications: The square root of 162 is used in various practical applications, from engineering calculations to financial modeling and beyond.
- Properties: Since 162 is not a perfect square, its square root is an irrational number, which cannot be expressed as a simple fraction but has a non-terminating, non-repeating decimal representation.
By mastering the concept of square roots, particularly for numbers like 162, learners can improve their problem-solving abilities and analytical thinking. This knowledge is not only crucial for academic success but also for understanding and navigating many real-life situations.
Khám phá cách giải một vấn đề căn bậc hai phức tạp trong video này. Học cách giải phương trình với √162 và các kỹ thuật toán học khác.
Một Vấn Đề Căn Bậc Hai Khó Khăn X/✓128=✓162/X | Giải Phương Trình | Toán Học...
READ MORE:
Tìm hiểu cách tính căn bậc hai của 162 trong video này. Video hướng dẫn chi tiết và các ứng dụng toán học liên quan.
Căn Bậc Hai Của 162