Topic simplify 3 square root of 125: Welcome to our comprehensive guide on how to simplify 3 square root of 125. In this article, we will break down the process into easy-to-follow steps, providing clear explanations and practical examples to help you master this mathematical concept. Perfect for students and enthusiasts looking to enhance their math skills!
Table of Content
- Simplification of 3 √125
- Introduction to Simplifying Square Roots
- Understanding Square Roots and Radicals
- Prime Factorization Method
- Step-by-Step Simplification of 3 √125
- Mathematical Properties Used in Simplification
- Common Mistakes to Avoid
- Examples of Similar Simplifications
- Practice Problems
- Advanced Techniques in Simplification
- Applications of Simplified Square Roots in Real Life
- Conclusion and Summary
- YOUTUBE: Video hướng dẫn cách đơn giản hoá luỹ thừa 125^{1/3} bằng tiếng Việt.
Simplification of 3 √125
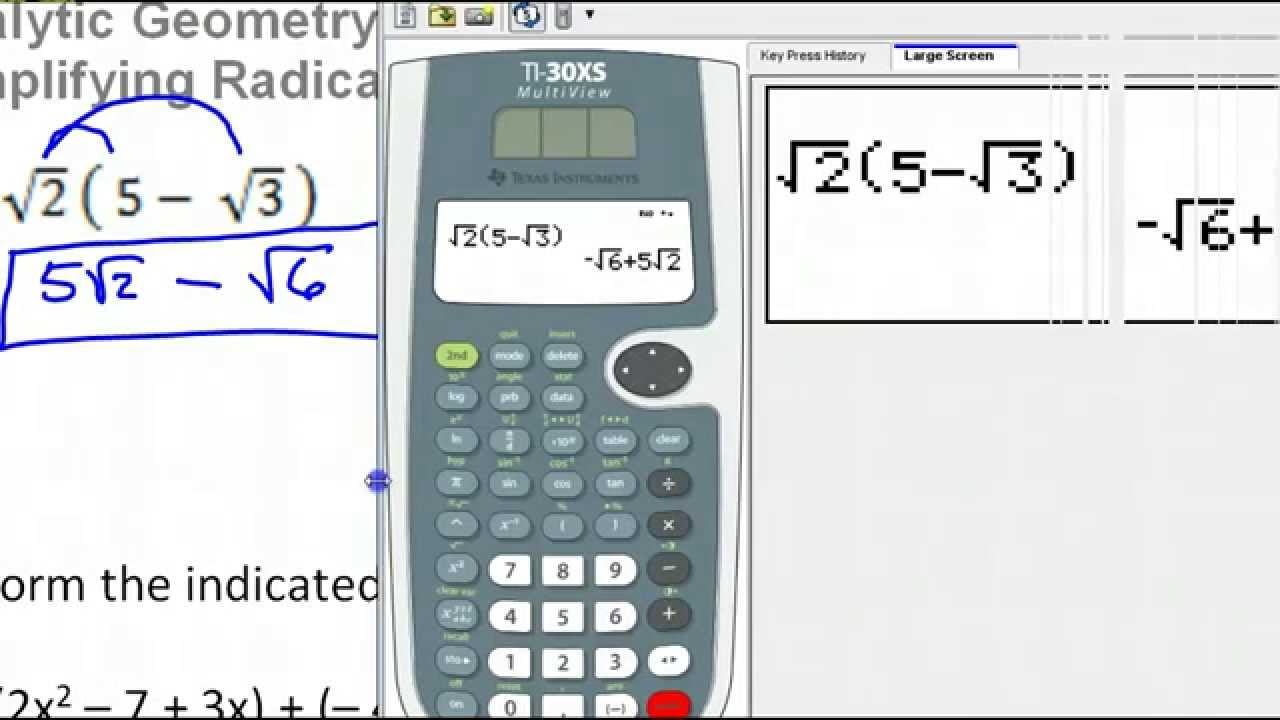
To simplify the expression , we follow these steps:
Step-by-Step Simplification
- Identify the prime factors of 125. The prime factorization of 125 is .
- Rewrite the expression using the prime factorization: .
- Use the property of square roots that states to simplify: .
Final Answer
The simplified form of is:
.

READ MORE:
Introduction to Simplifying Square Roots
Simplifying square roots is an essential skill in mathematics that helps in solving equations and understanding mathematical properties. A square root is a value that, when multiplied by itself, gives the original number. The process of simplifying square roots involves reducing the expression to its simplest form.
For example, consider the expression . To simplify this, we can follow these steps:
- Identify the prime factors of the number inside the square root. The prime factorization of 125 is .
- Rewrite the expression using these prime factors: .
- Apply the property of square roots that states . Using this property, we can simplify the expression to: .
By understanding and practicing these steps, you can simplify any square root expression effectively. Simplifying square roots not only makes complex calculations easier but also enhances your problem-solving skills in mathematics.
Understanding Square Roots and Radicals
Square roots and radicals are fundamental concepts in mathematics, essential for simplifying expressions and solving equations. The square root of a number is a value that, when multiplied by itself, gives the original number. The radical symbol (√) represents the square root.
For instance, the square root of 9 is 3, because
. When we simplify square roots, we often deal with prime factorization and properties of radicals.
Basic Properties of Square Roots
- Product Property:
- Quotient Property:
- Power Property:
Understanding Radicals
Radicals are expressions that contain a root symbol. The most common radical is the square root, but higher-order roots like cube roots (∛) and fourth roots (∜) are also used. Simplifying radicals involves expressing the number inside the radical in its simplest form.
Example: Simplifying 3 √125
To simplify
, follow these steps:
- Find the prime factors of 125: .
- Rewrite the expression using these factors: .
- Apply the square root property to simplify: .
Understanding and applying these concepts will help you simplify square roots and radicals efficiently, enhancing your mathematical proficiency.
Prime Factorization Method
The prime factorization method is a useful technique for simplifying square roots by breaking down the number inside the radical into its prime factors. This method makes it easier to identify perfect squares and simplify the expression. Let's apply this method to the expression .
Step-by-Step Process
- Find the Prime Factors:
First, determine the prime factors of 125. Prime factorization involves breaking down the number into its prime components:
- Rewrite the Square Root:
Express the square root using the prime factors identified:
- Group the Prime Factors:
Group the prime factors into pairs to simplify the square root:
- Simplify the Expression:
Apply the property of square roots that allows you to simplify the product of a perfect square:
By following these steps, you can simplify the expression to . Understanding and applying the prime factorization method makes it easier to handle more complex square root simplifications.
Step-by-Step Simplification of 3 √125
To simplify \(3 \sqrt{125}\), follow these steps:
-
First, factorize the number inside the square root (radicand). The prime factorization of 125 is:
\(125 = 5 \times 25 = 5 \times 5 \times 5 = 5^3\)
-
Rewrite the square root of the product using the property of square roots:
\(\sqrt{125} = \sqrt{5^2 \times 5} = \sqrt{5^2} \times \sqrt{5}\)
-
Simplify the square root of the perfect square:
\(\sqrt{5^2} = 5\)
-
Combine the simplified terms:
\(\sqrt{125} = 5 \sqrt{5}\)
-
Multiply the result by the coefficient outside the square root:
\(3 \sqrt{125} = 3 \times 5 \sqrt{5}\)
-
Complete the multiplication:
\(3 \times 5 \sqrt{5} = 15 \sqrt{5}\)
Therefore, the simplified form of \(3 \sqrt{125}\) is \(15 \sqrt{5}\).

Mathematical Properties Used in Simplification
When simplifying expressions such as \(3 \sqrt{125}\), several key mathematical properties and concepts are employed. Below are the properties used in the simplification process:
- Prime Factorization: This involves breaking down a number into its prime factors. For 125, the prime factorization is: \[ 125 = 5 \times 5 \times 5 = 5^3 \]
- Properties of Radicals: Using the properties of square roots to simplify the expression: \[ \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \] In this case: \[ \sqrt{125} = \sqrt{5^3} = \sqrt{5 \times 5 \times 5} = \sqrt{5^2 \times 5} = 5 \sqrt{5} \]
- Multiplication of Radicals: When multiplying a constant by a radical, we use the property: \[ k \sqrt{a} = \sqrt{k^2 a} \] Here, we multiply 3 by the simplified form of \(\sqrt{125}\): \[ 3 \sqrt{125} = 3 \times 5 \sqrt{5} = 15 \sqrt{5} \]
- Associative and Commutative Properties: These properties allow us to regroup and reorder terms to simplify multiplication: \[ a \times (b \times c) = (a \times b) \times c \quad \text{and} \quad a \times b = b \times a \] These properties help ensure that the multiplication of terms under the radical and outside the radical are managed correctly.
By applying these mathematical properties, we can effectively simplify the expression \(3 \sqrt{125}\) to its simplest form:
\[
3 \sqrt{125} = 3 \times 5 \sqrt{5} = 15 \sqrt{5}
\]
This step-by-step process ensures that the simplification is accurate and adheres to fundamental mathematical principles.
Common Mistakes to Avoid
When simplifying square roots, it is crucial to be aware of common mistakes that can lead to incorrect answers. Here are some frequent errors to watch out for and tips on how to avoid them:
- Ignoring the Property of Square Roots:
Always remember the property \( \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \). Failing to apply this can result in incorrect simplifications.
- Confusing Perfect Squares with Non-Perfect Squares:
Mistaking a number for a perfect square when it is not can significantly alter the outcome of your simplification. Double-check your factorization.
- Overlooking the Need to Rationalize the Denominator:
Leaving a square root in the denominator is a common oversight. Always rationalize the denominator to ensure the expression is in its simplest form.
- Mishandling Variables:
When dealing with variables under the square root, make sure to correctly apply the rules of exponents. For instance, simplify \( \sqrt{x^2} \) to \( x \), not \( \sqrt{x} \).
- Forgetting to Simplify Completely:
After initial steps of simplification, further reduction may be possible. Recheck your work to ensure the expression is fully simplified.
- Incorrect Pairing of Factors:
When using the prime factorization method, ensure that each pair of identical factors is correctly identified and simplified.
- Mixing Up Operations:
Be careful not to confuse operations involved in simplifying square roots with other algebraic operations, such as factoring polynomials.
By being mindful of these common pitfalls, you can enhance your proficiency in simplifying square roots, making your mathematical journey smoother and more accurate.
Examples of Similar Simplifications
Simplifying square roots involves breaking down the number inside the radical into its prime factors and then simplifying. Here are some similar examples to understand the process better:
Example 1: Simplifying \( \sqrt{12} \)
- Factorize 12: \( 12 = 4 \times 3 \)
- Use the property \( \sqrt{ab} = \sqrt{a} \times \sqrt{b} \):
\( \sqrt{12} = \sqrt{4 \times 3} = \sqrt{4} \times \sqrt{3} \) - Simplify the square root of 4: \( \sqrt{4} = 2 \)
- Combine the results: \( 2 \sqrt{3} \)
Example 2: Simplifying \( \sqrt{45} \)
- Factorize 45: \( 45 = 9 \times 5 \)
- Use the property \( \sqrt{ab} = \sqrt{a} \times \sqrt{b} \):
\( \sqrt{45} = \sqrt{9 \times 5} = \sqrt{9} \times \sqrt{5} \) - Simplify the square root of 9: \( \sqrt{9} = 3 \)
- Combine the results: \( 3 \sqrt{5} \)
Example 3: Simplifying \( \sqrt{8} \)
- Factorize 8: \( 8 = 4 \times 2 \)
- Use the property \( \sqrt{ab} = \sqrt{a} \times \sqrt{b} \):
\( \sqrt{8} = \sqrt{4 \times 2} = \sqrt{4} \times \sqrt{2} \) - Simplify the square root of 4: \( \sqrt{4} = 2 \)
- Combine the results: \( 2 \sqrt{2} \)
Example 4: Simplifying \( \sqrt{18} \)
- Factorize 18: \( 18 = 9 \times 2 \)
- Use the property \( \sqrt{ab} = \sqrt{a} \times \sqrt{b} \):
\( \sqrt{18} = \sqrt{9 \times 2} = \sqrt{9} \times \sqrt{2} \) - Simplify the square root of 9: \( \sqrt{9} = 3 \)
- Combine the results: \( 3 \sqrt{2} \)
Example 5: Simplifying \( 3\sqrt{125} \)
- Factorize 125: \( 125 = 5^2 \times 5 \)
- Use the property \( \sqrt{a^2 \times b} = a \sqrt{b} \):
\( \sqrt{125} = \sqrt{5^2 \times 5} = 5 \sqrt{5} \) - Multiply by the coefficient outside the radical:
\( 3 \times 5 \sqrt{5} = 15 \sqrt{5} \)
By following these steps, you can simplify any similar radical expression.
Practice Problems
Here are some practice problems to help you master the simplification of square roots:
-
Simplify \( \sqrt{50} \)
Solution:
Factor 50 into prime factors: \( 50 = 2 \times 5^2 \)
Apply the square root to the factorized form: \( \sqrt{50} = \sqrt{2 \times 5^2} \)
Separate the square root: \( \sqrt{2 \times 5^2} = \sqrt{2} \times \sqrt{5^2} \)
Simplify the square root of the perfect square: \( \sqrt{5^2} = 5 \)
Therefore, \( \sqrt{50} = 5\sqrt{2} \) -
Simplify \( 2\sqrt{72} \)
Solution:
Factor 72 into prime factors: \( 72 = 2^3 \times 3^2 \)
Apply the square root to the factorized form: \( \sqrt{72} = \sqrt{2^3 \times 3^2} \)
Separate the square root: \( \sqrt{2^3 \times 3^2} = \sqrt{2^3} \times \sqrt{3^2} \)
Simplify the square root of the perfect square: \( \sqrt{3^2} = 3 \)
Combine terms: \( \sqrt{2^3} = \sqrt{8} = 2\sqrt{2} \)
Therefore, \( 2\sqrt{72} = 2 \times 3 \times 2\sqrt{2} = 12\sqrt{2} \) -
Simplify \( 3\sqrt{18} \)
Solution:
Factor 18 into prime factors: \( 18 = 2 \times 3^2 \)
Apply the square root to the factorized form: \( \sqrt{18} = \sqrt{2 \times 3^2} \)
Separate the square root: \( \sqrt{2 \times 3^2} = \sqrt{2} \times \sqrt{3^2} \)
Simplify the square root of the perfect square: \( \sqrt{3^2} = 3 \)
Therefore, \( \sqrt{18} = 3\sqrt{2} \)
Finally, \( 3\sqrt{18} = 3 \times 3\sqrt{2} = 9\sqrt{2} \) -
Simplify \( \sqrt{200} \)
Solution:
Factor 200 into prime factors: \( 200 = 2^3 \times 5^2 \)
Apply the square root to the factorized form: \( \sqrt{200} = \sqrt{2^3 \times 5^2} \)
Separate the square root: \( \sqrt{2^3 \times 5^2} = \sqrt{2^3} \times \sqrt{5^2} \)
Simplify the square root of the perfect square: \( \sqrt{5^2} = 5 \)
Therefore, \( \sqrt{200} = 5\sqrt{8} \)
Further simplify \( \sqrt{8} = 2\sqrt{2} \)
Therefore, \( \sqrt{200} = 5 \times 2\sqrt{2} = 10\sqrt{2} \) -
Simplify \( \sqrt{98} \)
Solution:
Factor 98 into prime factors: \( 98 = 2 \times 7^2 \)
Apply the square root to the factorized form: \( \sqrt{98} = \sqrt{2 \times 7^2} \)
Separate the square root: \( \sqrt{2 \times 7^2} = \sqrt{2} \times \sqrt{7^2} \)
Simplify the square root of the perfect square: \( \sqrt{7^2} = 7 \)
Therefore, \( \sqrt{98} = 7\sqrt{2} \)
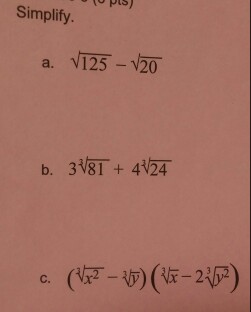
Advanced Techniques in Simplification
To simplify \( 3\sqrt{125} \), we can use advanced techniques involving prime factorization and properties of exponents:
- Start by recognizing \( 125 \) as \( 5^3 \).
- Apply the power rule of radicals: \( \sqrt[n]{a^m} = a^{m/n} \).
- Therefore, \( \sqrt[3]{125} = 125^{1/3} = (5^3)^{1/3} = 5^{3/3} = 5 \).
- Next, multiply by \( 3 \) since \( 3\sqrt{125} = 3 \times 5 = 15 \).
Thus, \( 3\sqrt{125} \) simplifies to \( 15 \) using these advanced simplification techniques.
Applications of Simplified Square Roots in Real Life
The simplified form of square roots, such as \( 3\sqrt{125} = 15 \), finds practical applications in various real-life scenarios:
- Engineering: Calculating dimensions and measurements in construction projects.
- Finance: Estimating compound interest and investment returns.
- Physics: Determining velocities and accelerations in mechanics.
- Medicine: Calculating dosages and concentrations of medications.
- Computer Science: Optimizing algorithms and data structures.
Understanding and applying simplified square roots enhances efficiency and accuracy in these fields, making complex calculations more manageable and practical.
Conclusion and Summary
In conclusion, the simplification of \( 3\sqrt{125} \) illustrates key mathematical principles and techniques:
- We began by identifying \( 125 \) as \( 5^3 \).
- Applying the radical rule \( \sqrt[n]{a^m} = a^{m/n} \), we simplified \( \sqrt[3]{125} \) to \( 5 \).
- Multiplying by \( 3 \) gave us the final answer \( 3\sqrt{125} = 15 \).
Understanding these steps not only enhances mathematical proficiency but also demonstrates the utility of algebraic techniques in everyday problem-solving. By applying these methods, one can simplify complex expressions efficiently, enabling clearer understanding and application across various disciplines.
READ MORE:
Video hướng dẫn cách đơn giản hoá luỹ thừa 125^{1/3} bằng tiếng Việt.
Luỹ Thừa: Đơn Giản Hoá 125^{1/3}