Topic parallelogram perimeter: Understanding the perimeter of a parallelogram is essential for students and geometry enthusiasts alike. This comprehensive guide will walk you through the definition, properties, and step-by-step methods to calculate the perimeter, complete with practical examples and tips. Dive in to master the concept and enhance your mathematical skills.
Table of Content
- Understanding the Perimeter of a Parallelogram
- Introduction to Parallelogram Perimeter
- Definition and Properties of a Parallelogram
- Basic Formula for Calculating Perimeter
- Step-by-Step Guide to Perimeter Calculation
- Examples and Practical Applications
- Special Cases in Perimeter Calculation
- Common Mistakes to Avoid
- Advanced Perimeter Formulas
- Comparing Parallelogram with Other Shapes
- Practice Problems and Solutions
- Visual Aids and Diagrams
- Conclusion and Summary
- YOUTUBE: Video này hướng dẫn cách tìm chu vi của hình bình hành một cách dễ hiểu và chi tiết.
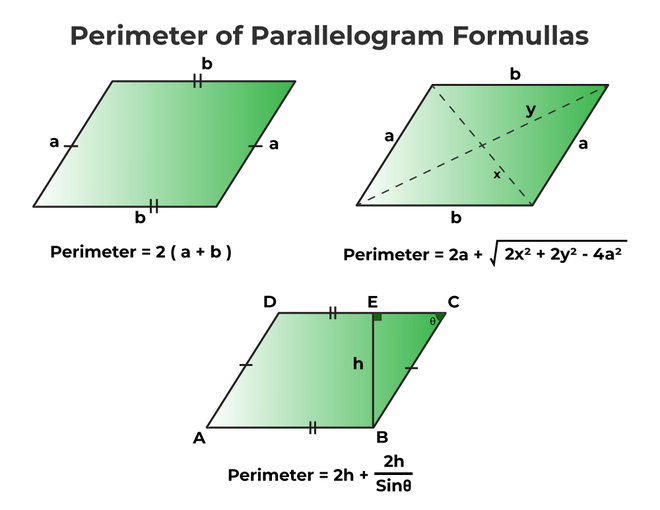
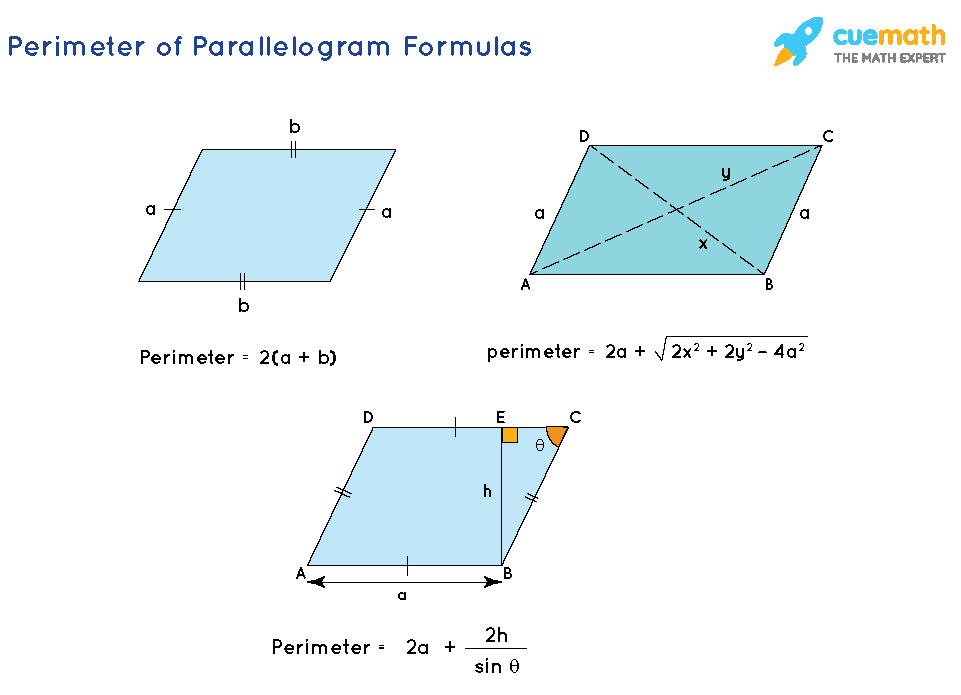
Understanding the Perimeter of a Parallelogram
A parallelogram is a quadrilateral with opposite sides that are both equal in length and parallel. Calculating the perimeter of a parallelogram is straightforward and involves summing the lengths of all its sides.
Formula for the Perimeter of a Parallelogram
The formula to find the perimeter of a parallelogram is:
Where a and b are the lengths of the adjacent sides of the parallelogram.
Steps to Calculate the Perimeter
- Identify the lengths of the two adjacent sides of the parallelogram.
- Sum these lengths.
- Multiply the result by 2 to get the perimeter.
Example Calculation
Let's consider a parallelogram with side lengths 8 cm and 5 cm. To find the perimeter:
-
Sum the lengths of the sides:
-
Multiply by 2:
Therefore, the perimeter of the parallelogram is 26 cm.
Summary
The perimeter of a parallelogram is a simple yet essential property that can be calculated using the formula
.
By understanding and applying this formula, you can easily determine the perimeter of any parallelogram given the lengths of its sides.
READ MORE:
Introduction to Parallelogram Perimeter
A parallelogram is a four-sided polygon with opposite sides that are equal in length and parallel. The perimeter of a parallelogram is the total distance around the shape, which can be calculated by adding the lengths of all four sides. Understanding the concept of perimeter is crucial in various fields such as architecture, engineering, and everyday problem-solving.
To calculate the perimeter of a parallelogram, you need to know the lengths of its two pairs of opposite sides. The formula for the perimeter P is given by:
Where a and b are the lengths of the two pairs of opposite sides. This formula arises from the fact that each pair of opposite sides in a parallelogram is equal.
Let's break down the calculation into steps:
- Identify the lengths of the two pairs of opposite sides. Let's call them a and b.
- Add the lengths of these sides together: a + b.
- Multiply the sum by 2 to account for both pairs of sides: 2 × (a + b).
This simple yet effective method ensures you can quickly determine the perimeter of any parallelogram, provided you know the lengths of its sides.
Understanding the perimeter is essential for various applications, including:
- Construction: Knowing the perimeter helps in estimating materials needed for building projects.
- Landscaping: Calculating the perimeter is useful for planning borders and fencing.
- Design: Helps in creating geometric patterns and designs where precise measurements are crucial.
With this foundational knowledge, you are now prepared to delve deeper into the specifics of calculating and applying the perimeter of a parallelogram.
Definition and Properties of a Parallelogram
A parallelogram is a four-sided polygon (quadrilateral) with opposite sides that are parallel and equal in length. Here are some key properties and definitions associated with parallelograms:
- Opposite Sides are Equal: In a parallelogram, both pairs of opposite sides are equal in length. If the sides are labeled as \(AB\), \(BC\), \(CD\), and \(DA\), then \(AB = CD\) and \(BC = DA\).
- Opposite Angles are Equal: The opposite angles in a parallelogram are equal. If the angles are labeled as \( \angle A\), \( \angle B\), \( \angle C\), and \( \angle D\), then \( \angle A = \angle C\) and \( \angle B = \angle D\).
- Adjacent Angles are Supplementary: Any two adjacent angles in a parallelogram add up to \(180^\circ\). For example, \( \angle A + \angle B = 180^\circ\).
- Diagonals Bisect Each Other: The diagonals of a parallelogram bisect each other. This means that each diagonal divides the parallelogram into two congruent triangles.
The following table summarizes these properties:
| Property | Description |
|---|---|
| Opposite Sides | Equal in length (\(AB = CD\) and \(BC = DA\)) |
| Opposite Angles | Equal (\( \angle A = \angle C\) and \( \angle B = \angle D\)) |
| Adjacent Angles | Supplementary (\( \angle A + \angle B = 180^\circ\)) |
| Diagonals | Bisect each other |
Additionally, if the parallelogram has sides of length \(a\) and \(b\), the perimeter \(P\) can be calculated using the formula:
\( P = 2(a + b) \)
Basic Formula for Calculating Perimeter
The perimeter of a parallelogram is the total distance around its outer boundary. The basic formula for calculating the perimeter involves the lengths of its sides. For a parallelogram with sides of length a and b, the perimeter P can be calculated using the following formula:
Perimeter = 2(a + b)
Here's a step-by-step guide to using this formula:
- Identify the lengths of the sides: Measure or obtain the lengths of the two adjacent sides of the parallelogram. Let's denote these lengths as a and b.
- Apply the formula: Substitute the values of a and b into the formula. Multiply the sum of a and b by 2 to find the perimeter.
For example, if a parallelogram has sides of length 5 cm and 8 cm, the calculation would be:
P = 2(5 cm + 8 cm) = 2(13 cm) = 26 cm
Thus, the perimeter of the parallelogram is 26 cm.
Additional Formulas for Special Cases
In some cases, you might have different sets of data such as the lengths of the diagonals or angles. Here are additional formulas that can be used:
- If you know the lengths of the sides and the diagonals (d1 and d2), you can use the formula:
P = 2a + sqrt(2(d12 + d22 - 2a2))
- If you know the length of a side (a), the height (h), and an angle (θ), the formula is:
P = 2a + 2h / sin(θ)
Example Calculations
Here are a couple of example problems to illustrate the application of these formulas:
- Example 1: Find the perimeter of a parallelogram with side lengths of 7 cm and 9 cm.
P = 2(7 cm + 9 cm) = 2(16 cm) = 32 cm
- Example 2: Given a parallelogram with side length 10 cm, height 12 cm, and an angle of 30 degrees, find its perimeter.
P = 2(10 cm) + 2(12 cm) / sin(30°) = 20 cm + 48 cm = 68 cm
Step-by-Step Guide to Perimeter Calculation
Calculating the perimeter of a parallelogram involves a straightforward process. Here’s a step-by-step guide to help you understand and calculate the perimeter efficiently:
-
Identify the lengths of the sides:
First, identify the lengths of any two adjacent sides of the parallelogram. Let's call these sides \( a \) and \( b \).
-
Understand the perimeter formula:
The formula for the perimeter (\( P \)) of a parallelogram is:
\[
P = 2a + 2b
\]Where \( a \) and \( b \) are the lengths of the adjacent sides.
-
Measure the sides:
Using a ruler or measuring tape, measure the lengths of the sides \( a \) and \( b \). Ensure the measurements are in the same unit (e.g., centimeters or inches).
-
Apply the formula:
Insert the measured values of \( a \) and \( b \) into the formula:
\[
P = 2a + 2b
\] -
Calculate the perimeter:
Multiply the sum of \( a \) and \( b \) by 2 to get the perimeter:
\[
P = 2(a + b)
\]This gives you the total perimeter of the parallelogram.
Here are a few examples to illustrate the process:
-
Example 1: A parallelogram with sides \( a = 6 \) cm and \( b = 4 \) cm.
Using the formula:
\[
P = 2(6 \, \text{cm} + 4 \, \text{cm}) = 2(10 \, \text{cm}) = 20 \, \text{cm}
\] -
Example 2: A parallelogram with sides \( a = 10 \) cm and \( b = 7 \) cm.
Using the formula:
\[
P = 2(10 \, \text{cm} + 7 \, \text{cm}) = 2(17 \, \text{cm}) = 34 \, \text{cm}
\]
Remember, the key steps involve measuring the sides accurately and applying the perimeter formula correctly. With practice, calculating the perimeter of a parallelogram will become second nature.

Examples and Practical Applications
Understanding how to calculate the perimeter of a parallelogram is not only important in geometry but also in various practical applications such as construction, design, and problem-solving. Here, we provide some examples and practical applications to illustrate these concepts.
Example 1: Simple Perimeter Calculation
Consider a parallelogram with the following dimensions:
- Base (b): 5 cm
- Side (a): 7 cm
Using the perimeter formula for a parallelogram:
\[
P = 2(a + b)
\]
Substitute the given values:
\[
P = 2(7 \, \text{cm} + 5 \, \text{cm}) = 2 \times 12 \, \text{cm} = 24 \, \text{cm}
\]
Therefore, the perimeter of the parallelogram is 24 cm.
Example 2: Real-Life Application in Construction
Imagine a builder needs to create a garden bed in the shape of a parallelogram with the following dimensions:
- Base (b): 8 feet
- Side (a): 10 feet
To determine the amount of fencing needed, the builder calculates the perimeter:
\[
P = 2(a + b)
\]
Substitute the given values:
\[
P = 2(10 \, \text{ft} + 8 \, \text{ft}) = 2 \times 18 \, \text{ft} = 36 \, \text{ft}
\]
The builder will need 36 feet of fencing to enclose the garden bed.
Example 3: Perimeter in Design and Art
In a design project, an artist wants to create a parallelogram-shaped frame with:
- Base (b): 12 inches
- Side (a): 15 inches
The artist calculates the perimeter to determine the length of the border material needed:
\[
P = 2(a + b)
\]
Substitute the given values:
\[
P = 2(15 \, \text{in} + 12 \, \text{in}) = 2 \times 27 \, \text{in} = 54 \, \text{in}
\]
Thus, the artist will require 54 inches of border material for the frame.
Practical Applications
- Landscaping: Calculating the perimeter of garden beds, pathways, and other landscape features.
- Construction: Determining the perimeter of floors, roofs, and other parallelogram-shaped structures.
- Interior Design: Creating and framing artwork or designing furniture with parallelogram shapes.
- Mathematical Problem-Solving: Applying perimeter formulas in geometry problems and real-world scenarios.
Special Cases in Perimeter Calculation
While the basic formula for calculating the perimeter of a parallelogram is , special cases such as rectangles, rhombuses, and squares introduce unique properties that can affect the perimeter calculation.
1. Rectangle
A rectangle is a type of parallelogram where all angles are right angles (90°) and opposite sides are equal. The perimeter of a rectangle can be calculated using the formula:
Where is the length and is the width. For example, if a rectangle has a length of 10 units and a width of 5 units, its perimeter would be:
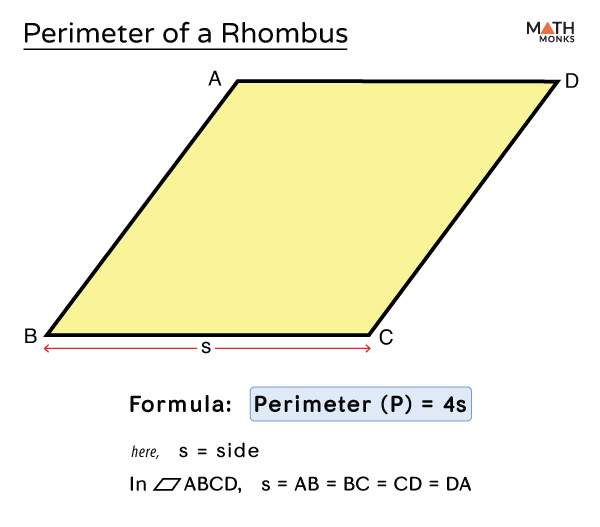
2. Rhombus
A rhombus is a parallelogram with all four sides of equal length. The perimeter of a rhombus can be calculated using the formula:
Where is the length of a side. For example, if each side of a rhombus is 7 units, its perimeter would be:
3. Square
A square is a special type of rhombus where all four sides are equal and all angles are 90°. The perimeter of a square can be calculated using the same formula as for a rhombus:
For example, if each side of a square is 6 units, its perimeter would be:
Examples
- Rectangle: A book has a length of 8 inches and a width of 5 inches. The perimeter is inches.
- Rhombus: A diamond-shaped sign with each side measuring 4 feet has a perimeter of feet.
- Square: A chessboard with each side measuring 12 inches has a perimeter of inches.
Understanding these special cases helps in visualizing and solving problems related to the perimeter of parallelograms more effectively.
Common Mistakes to Avoid
When calculating the perimeter of a parallelogram, there are several common mistakes that can lead to incorrect results. Recognizing and avoiding these errors is crucial for accurate calculations:
- Confusing perimeter with area: Remember, the perimeter is the total distance around the parallelogram, while the area represents the space enclosed within it. Do not use the area formula (\(A = \text{base} \times \text{height}\)) to calculate the perimeter.
- Misidentifying the sides: Ensure you are using the lengths of the sides and not the diagonals of the parallelogram. The perimeter calculation requires the lengths of the actual sides.
- Forgetting opposite sides are equal: A parallelogram has two pairs of equal sides. Make sure to double each side length once, not adding all four sides individually if only two side lengths are known.
- Incorrect addition: Simple arithmetic errors in adding the lengths of sides can skew the perimeter calculation. Double-check your sums for accuracy.
- Forgetting to multiply by two: The most common oversight is neglecting to multiply the sum of the side lengths by two. Remember, the formula is \(P = 2(a + b)\), not just \(a + b\).
- Not using consistent units: Mixing units (e.g., meters and centimeters) without conversion can result in incorrect perimeter values. Ensure all measurements are in the same unit before calculating.
To avoid these errors:
- Clearly label each side of the parallelogram as you identify them.
- Use a calculator for addition and multiplication to minimize arithmetic errors.
- Review the formula before starting your calculation to ensure you multiply by two.
- Convert all measurements to the same unit before performing any calculations.
By paying attention to these details, you can ensure accurate and error-free calculations of the perimeter of a parallelogram.
Advanced Perimeter Formulas
The perimeter of a parallelogram is generally calculated using the formula:
\[ P = 2(a + b) \]
where \( a \) and \( b \) are the lengths of the adjacent sides. However, there are more advanced scenarios and formulas to consider:
Using Diagonals and One Side
If one side \( a \) and the lengths of the diagonals \( d_1 \) and \( d_2 \) are known, the perimeter can be calculated using the formula:
\[ P = 2a + \sqrt{2d_1^2 + 2d_2^2 - 4a^2} \]
Example: For \( a = 7 \) units, \( d_1 = 8 \) units, and \( d_2 = 10 \) units, the perimeter is:
\[ P = 2 \times 7 + \sqrt{2 \times 8^2 + 2 \times 10^2 - 4 \times 7^2} \approx 25.49 \, \text{units} \]
Using Base, Height, and Angle
If the base \( b \), height \( h \), and an angle \( \theta \) are known, the perimeter can be calculated as:
\[ P = 2b + \frac{2h}{\sin \theta} \]
Example: For \( b = 15 \) yards, \( h = 20 \) yards, and \( \theta = 30^\circ \), the perimeter is:
\[ P = 2 \times 15 + \frac{2 \times 20}{\sin 30^\circ} = 110 \, \text{yards} \]
Using Only One Side and Height
If the side \( a \) and the height \( h \) are given, and the corresponding angle \( \theta \) is known, the side \( b \) can be calculated using the cosine rule:
\[ b = \frac{h}{\cos \theta} \]
Then, the perimeter can be found as:
\[ P = 2(a + b) \]
Example: Given \( a = 8 \) cm, \( h = 4 \) cm, and \( \theta = 60^\circ \), find \( b \) and the perimeter:
\[ b = \frac{4}{\cos 60^\circ} = 8 \, \text{cm} \]
\[ P = 2(8 + 8) = 32 \, \text{cm} \]
Perimeter from Area and One Side
If the area \( A \) and one side \( a \) are known, the other side \( b \) can be determined using:
\[ b = \frac{A}{h} \]
where \( h \) is the height, which can be derived from the area:
\[ h = \frac{A}{a} \]
Then the perimeter is:
\[ P = 2(a + b) \]
Example: Given \( A = 72 \, \text{cm}^2 \) and \( a = 18 \, \text{cm} \), find \( b \) and the perimeter:
\[ h = \frac{72}{18} = 4 \, \text{cm} \]
\[ b = \frac{72}{4} = 18 \, \text{cm} \]
\[ P = 2(18 + 18) = 72 \, \text{cm} \]
Comparing Parallelogram with Other Shapes
A parallelogram is a special type of quadrilateral with unique properties. To understand its characteristics better, let's compare it with other common shapes such as rectangles, squares, rhombuses, and trapezoids.
-
Parallelogram vs. Rectangle
Both parallelograms and rectangles have opposite sides that are parallel and equal in length. However, in a rectangle, all interior angles are right angles (90 degrees).
Property Parallelogram Rectangle Sides Opposite sides are equal and parallel Opposite sides are equal and parallel Angles Opposite angles are equal All angles are 90° -
Parallelogram vs. Square
A square is a type of parallelogram with all sides equal in length and all angles equal to 90 degrees. Therefore, every square is a parallelogram, but not every parallelogram is a square.
Property Parallelogram Square Sides Opposite sides are equal and parallel All sides are equal and parallel Angles Opposite angles are equal All angles are 90° -
Parallelogram vs. Rhombus
A rhombus is another special type of parallelogram where all sides are equal in length. The diagonals of a rhombus bisect each other at right angles.
Property Parallelogram Rhombus Sides Opposite sides are equal and parallel All sides are equal Angles Opposite angles are equal Opposite angles are equal Diagonals Bisect each other Bisect each other at right angles -
Parallelogram vs. Trapezoid
A trapezoid (or trapezium in the UK) has only one pair of parallel sides, while a parallelogram has two pairs of parallel sides.
Property Parallelogram Trapezoid Sides Two pairs of parallel sides One pair of parallel sides Angles Opposite angles are equal No specific angle properties
In summary, while parallelograms share some properties with other quadrilaterals, they have distinct features that set them apart. Understanding these differences is crucial for solving geometry problems and for practical applications in design and architecture.
Practice Problems and Solutions
Here are some practice problems along with detailed solutions to help you understand the perimeter calculation of a parallelogram:
-
Problem 1: Find the perimeter of a parallelogram whose two adjacent sides are 6 cm and 8 cm.
Solution:
Given:
- Side \( a = 6 \, \text{cm} \)
- Side \( b = 8 \, \text{cm} \)
The formula for the perimeter \( P \) of a parallelogram is:
\[ P = 2(a + b) \]
Substitute the given values:
\[ P = 2(6 \, \text{cm} + 8 \, \text{cm}) = 2 \times 14 \, \text{cm} = 28 \, \text{cm} \]
Therefore, the perimeter is 28 cm.
-
Problem 2: The perimeter of a parallelogram is 60 cm. One of its sides is 18 cm. Find the length of the other side.
Solution:
Given:
- Perimeter \( P = 60 \, \text{cm} \)
- One side \( a = 18 \, \text{cm} \)
We know the formula for the perimeter is:
\[ P = 2(a + b) \]
Substitute the given values and solve for \( b \):
\[ 60 = 2(18 + b) \]
\[ 60 = 36 + 2b \]
\[ 2b = 60 - 36 \]
\[ 2b = 24 \]
\[ b = \frac{24}{2} = 12 \, \text{cm} \]
Therefore, the length of the other side is 12 cm.
-
Problem 3: A parallelogram has sides in the ratio of 3:5. If its perimeter is 64 cm, find the lengths of its sides.
Solution:
Let the sides be \( 3x \) and \( 5x \).
Given the perimeter \( P = 64 \, \text{cm} \).
Using the perimeter formula:
\[ P = 2(3x + 5x) \]
\[ 64 = 2(8x) \]
\[ 64 = 16x \]
\[ x = \frac{64}{16} = 4 \]
Thus, the lengths of the sides are:
\[ 3x = 3 \times 4 = 12 \, \text{cm} \]
\[ 5x = 5 \times 4 = 20 \, \text{cm} \]
Therefore, the lengths of the sides are 12 cm and 20 cm.
-
Problem 4: The base of a parallelogram is 10 cm and its height is 6 cm. Find the perimeter if one of the interior angles is 30 degrees.
Solution:
Given:
- Base \( b = 10 \, \text{cm} \)
- Height \( h = 6 \, \text{cm} \)
- Angle \( \theta = 30^\circ \)
The length of the side \( a \) can be found using the height and the angle:
\[ a = \frac{h}{\sin \theta} = \frac{6}{\sin 30^\circ} = \frac{6}{0.5} = 12 \, \text{cm} \]
Now, use the perimeter formula:
\[ P = 2(a + b) = 2(12 \, \text{cm} + 10 \, \text{cm}) = 2 \times 22 \, \text{cm} = 44 \, \text{cm} \]
Therefore, the perimeter is 44 cm.
These practice problems are designed to solidify your understanding of calculating the perimeter of a parallelogram. Ensure you comprehend each step and try to solve similar problems for better mastery.
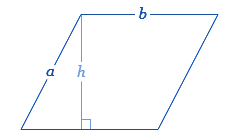
Visual Aids and Diagrams
Visual aids and diagrams are essential tools for understanding the properties and calculations related to parallelograms. They provide a clear representation of the shape and help in visualizing the geometric concepts. Below are some diagrams and explanations to aid in understanding the perimeter of a parallelogram.
Basic Diagram of a Parallelogram
The following diagram shows a basic parallelogram with sides labeled:

|
In this diagram, the parallelogram has two pairs of opposite sides. Let the lengths of the sides be \( a \) and \( b \). The formula for the perimeter \( P \) of the parallelogram is:
\[ P = 2a + 2b = 2(a + b) \]
Interactive Diagram
Interactive diagrams allow users to manipulate the shape and see how the perimeter changes with different side lengths. For example:
By dragging the points, you can resize the parallelogram and observe the changes in the perimeter calculation.
Perimeter Calculation with Base and Height
Sometimes, the base, height, and an interior angle are given, and the perimeter needs to be calculated. The following diagram illustrates this case:

|
Given:
- Base \( b \)
- Height \( h \)
- Angle \( \theta \)
The formula for the perimeter in this case is:
\[ P = 2 \left( b + \frac{h}{\cos \theta} \right) \]
Example Problem
Consider a parallelogram with a base of 10 cm, a height of 5 cm, and an angle of 30 degrees. The perimeter can be calculated as follows:
\[ P = 2 \left( 10 + \frac{5}{\cos 30^\circ} \right) \]
Using the value of \(\cos 30^\circ = \frac{\sqrt{3}}{2}\):
\[ P = 2 \left( 10 + \frac{5}{\frac{\sqrt{3}}{2}} \right) = 2 \left( 10 + \frac{10}{\sqrt{3}} \right) = 2 \left( 10 + \frac{10 \sqrt{3}}{3} \right) \approx 2 \left( 10 + 5.77 \right) = 2 \times 15.77 = 31.54 \, \text{cm} \]
Comparison with Other Shapes
It's helpful to compare the parallelogram with other quadrilaterals like rectangles and rhombuses to understand the differences in perimeter calculations:
| Shape | Diagram | Perimeter Formula |
|---|---|---|
| Parallelogram |  |
\( P = 2(a + b) \) |
| Rectangle |  |
\( P = 2(l + w) \) |
| Rhombus |  |
\( P = 4s \) |
These visual aids and diagrams provide a comprehensive understanding of how to calculate the perimeter of a parallelogram and compare it with other shapes.
Conclusion and Summary
The study of the perimeter of a parallelogram highlights its significance in understanding geometry and its practical applications. The perimeter is the total distance around the parallelogram, calculated using the formula:
\[ P = 2(a + b) \]
where \( a \) and \( b \) are the lengths of the adjacent sides. This straightforward formula allows for quick and easy calculations, essential for various mathematical and real-world applications.
Moreover, the versatility of the perimeter formula extends to situations where additional information such as diagonals or angles is provided. For instance:
- When the lengths of one side and both diagonals are known, the formula becomes:
- When the base, height, and an angle are given, another formula is used:
\[ P = 2a + \sqrt{2x^2 + 2y^2 - 4a^2} \]
\[ P = 2a + 2h / \sin(\theta) \]
Understanding these formulas not only aids in solving academic problems but also equips students and professionals with the tools to address real-life scenarios, such as in engineering and architecture, where precise measurements are crucial.
In summary, the perimeter of a parallelogram is a fundamental concept in geometry that provides insight into more complex geometric shapes and their properties. By mastering the basic and advanced formulas, one can efficiently solve problems and apply these principles in various practical contexts.
As you practice and explore more problems related to parallelogram perimeters, you will develop a deeper appreciation for the elegance and utility of geometric principles. Keep practicing with diverse examples to reinforce your understanding and enhance your problem-solving skills.
Video này hướng dẫn cách tìm chu vi của hình bình hành một cách dễ hiểu và chi tiết.
Làm Thế Nào Để Tìm Chu Vi Của Hình Bình Hành
READ MORE:
Video này hướng dẫn cách tìm diện tích và chu vi của hình bình hành một cách dễ hiểu và chi tiết.
Làm Thế Nào Để Tìm Diện Tích Và Chu Vi Của Hình Bình Hành