Topic ratio of perimeters: The ratio of perimeters is a fundamental concept in geometry that compares the perimeters of two shapes. This guide provides an in-depth look at the mathematical definitions, applications, and examples of perimeter ratios, making it essential for students, educators, and anyone interested in geometric principles.
Table of Content
- Ratio of Perimeters
- Ratio of Perimeters
- Introduction to Ratio of Perimeters
- Introduction to Ratio of Perimeters
- Mathematical Definition
- Mathematical Definition
- Applications of Ratio of Perimeters
- Applications of Ratio of Perimeters
- Examples of Ratio of Perimeters
- Examples of Ratio of Perimeters
- Ratio of Perimeters in Similar Shapes
- Ratio of Perimeters in Similar Shapes
- Scaling Figures and Perimeter Ratios
- Scaling Figures and Perimeter Ratios
- Practical Uses in Real-World Applications
- Practical Uses in Real-World Applications
- Comparison of Different Geometric Shapes
- Comparison of Different Geometric Shapes
- Ratio of Perimeters in Complex Figures
- Ratio of Perimeters in Complex Figures
- YOUTUBE:
Ratio of Perimeters
The ratio of the perimeters of two geometric shapes is a comparison of their boundary lengths. This ratio provides valuable insights into the relative sizes and scales of the shapes. Understanding the ratio of perimeters is crucial in various mathematical and practical applications.
Definition
If we have two geometric shapes, \( A \) and \( B \), with perimeters \( P_A \) and \( P_B \) respectively, the ratio of their perimeters is given by:
\[
\text{Ratio of Perimeters} = \frac{P_A}{P_B}
\]
Applications
- Scaling Figures: When scaling figures, the ratio of perimeters helps determine the proportional increase or decrease in the boundary lengths.
- Similarity in Geometry: Similar geometric shapes have perimeters that are proportional to their corresponding sides.
- Practical Use: In real-world applications, such as map scaling and model making, understanding perimeter ratios ensures accurate representations.
Examples
Consider two rectangles where the dimensions of rectangle \( A \) are twice the dimensions of rectangle \( B \). If the dimensions of rectangle \( B \) are \( l \) and \( w \), then the dimensions of rectangle \( A \) are \( 2l \) and \( 2w \).
The perimeter of rectangle \( B \) is:
\[
P_B = 2(l + w)
\]
The perimeter of rectangle \( A \) is:
\[
P_A = 2(2l + 2w) = 4(l + w)
\]
Therefore, the ratio of the perimeters is:
\[
\frac{P_A}{P_B} = \frac{4(l + w)}{2(l + w)} = 2
\]
This shows that the perimeter of rectangle \( A \) is twice that of rectangle \( B \).
Geometric Considerations
For similar shapes, the ratio of perimeters is equal to the ratio of any pair of corresponding side lengths. For example, if two triangles are similar with a side length ratio of \( k \), then their perimeter ratio will also be \( k \).
Mathematically, if two similar shapes have a side length ratio of \( k \), then:
\[
\frac{P_1}{P_2} = k
\]
Conclusion
Understanding the ratio of perimeters is essential in both theoretical and practical contexts. It helps in scaling geometric figures, understanding properties of similar shapes, and ensuring accurate real-world applications.

READ MORE:
Ratio of Perimeters
The ratio of the perimeters of two geometric shapes is a comparison of their boundary lengths. This ratio provides valuable insights into the relative sizes and scales of the shapes. Understanding the ratio of perimeters is crucial in various mathematical and practical applications.
Definition
If we have two geometric shapes, \( A \) and \( B \), with perimeters \( P_A \) and \( P_B \) respectively, the ratio of their perimeters is given by:
\[
\text{Ratio of Perimeters} = \frac{P_A}{P_B}
\]
Applications
- Scaling Figures: When scaling figures, the ratio of perimeters helps determine the proportional increase or decrease in the boundary lengths.
- Similarity in Geometry: Similar geometric shapes have perimeters that are proportional to their corresponding sides.
- Practical Use: In real-world applications, such as map scaling and model making, understanding perimeter ratios ensures accurate representations.
Examples
Consider two rectangles where the dimensions of rectangle \( A \) are twice the dimensions of rectangle \( B \). If the dimensions of rectangle \( B \) are \( l \) and \( w \), then the dimensions of rectangle \( A \) are \( 2l \) and \( 2w \).
The perimeter of rectangle \( B \) is:
\[
P_B = 2(l + w)
\]
The perimeter of rectangle \( A \) is:
\[
P_A = 2(2l + 2w) = 4(l + w)
\]
Therefore, the ratio of the perimeters is:
\[
\frac{P_A}{P_B} = \frac{4(l + w)}{2(l + w)} = 2
\]
This shows that the perimeter of rectangle \( A \) is twice that of rectangle \( B \).
Geometric Considerations
For similar shapes, the ratio of perimeters is equal to the ratio of any pair of corresponding side lengths. For example, if two triangles are similar with a side length ratio of \( k \), then their perimeter ratio will also be \( k \).
Mathematically, if two similar shapes have a side length ratio of \( k \), then:
\[
\frac{P_1}{P_2} = k
\]
Conclusion
Understanding the ratio of perimeters is essential in both theoretical and practical contexts. It helps in scaling geometric figures, understanding properties of similar shapes, and ensuring accurate real-world applications.

Introduction to Ratio of Perimeters
The ratio of perimeters is a crucial concept in geometry that helps in comparing the perimeters of two shapes. It is particularly useful when dealing with similar shapes, scaling, and understanding geometric properties. The ratio of perimeters can be defined and calculated using the formula:
Where P1 and P2 are the perimeters of the two shapes being compared.
Key considerations for understanding the ratio of perimeters include:
- For similar shapes, the ratio of the perimeters is equal to the ratio of the corresponding side lengths.
- If the shapes are scaled versions of each other, the perimeter ratio is the same as the scaling factor.
- This ratio helps in solving problems related to scaling in various real-world applications such as architecture and design.
Let's explore this concept further through definitions, applications, and examples in the subsequent sections.
Introduction to Ratio of Perimeters
The ratio of perimeters is a crucial concept in geometry that helps in comparing the perimeters of two shapes. It is particularly useful when dealing with similar shapes, scaling, and understanding geometric properties. The ratio of perimeters can be defined and calculated using the formula:
Where P1 and P2 are the perimeters of the two shapes being compared.
Key considerations for understanding the ratio of perimeters include:
- For similar shapes, the ratio of the perimeters is equal to the ratio of the corresponding side lengths.
- If the shapes are scaled versions of each other, the perimeter ratio is the same as the scaling factor.
- This ratio helps in solving problems related to scaling in various real-world applications such as architecture and design.
Let's explore this concept further through definitions, applications, and examples in the subsequent sections.
Mathematical Definition
The mathematical definition of the ratio of perimeters involves comparing the lengths of the perimeters of two shapes. This ratio can be expressed as:
Where:
- P1 is the perimeter of the first shape.
- P2 is the perimeter of the second shape.
To calculate the ratio of perimeters, follow these steps:
- Measure the perimeter of the first shape (P1).
- Measure the perimeter of the second shape (P2).
- Divide the perimeter of the first shape by the perimeter of the second shape to obtain the ratio:
This ratio is a dimensionless number that indicates how many times larger or smaller the perimeter of the first shape is compared to the second shape. For similar shapes, this ratio will be equal to the ratio of their corresponding side lengths.
For example, if two squares have side lengths of 2 and 4 units respectively, the ratio of their perimeters will be:
This means the perimeter of the smaller square is half that of the larger square.
Mathematical Definition
The mathematical definition of the ratio of perimeters involves comparing the lengths of the perimeters of two shapes. This ratio can be expressed as:
Where:
- P1 is the perimeter of the first shape.
- P2 is the perimeter of the second shape.
To calculate the ratio of perimeters, follow these steps:
- Measure the perimeter of the first shape (P1).
- Measure the perimeter of the second shape (P2).
- Divide the perimeter of the first shape by the perimeter of the second shape to obtain the ratio:
This ratio is a dimensionless number that indicates how many times larger or smaller the perimeter of the first shape is compared to the second shape. For similar shapes, this ratio will be equal to the ratio of their corresponding side lengths.
For example, if two squares have side lengths of 2 and 4 units respectively, the ratio of their perimeters will be:
This means the perimeter of the smaller square is half that of the larger square.
Applications of Ratio of Perimeters
The ratio of perimeters has various practical applications in geometry, engineering, architecture, and everyday problem-solving. Understanding this concept allows for better design, analysis, and scaling of objects and structures. Here are some key applications:
- Architecture and Design:
In architecture, the ratio of perimeters is crucial for scaling models of buildings. Architects use this ratio to create accurate scale models that preserve the proportions of the original structure. This helps in visualizing the final product and ensuring structural integrity.
- Engineering:
Engineers often use the ratio of perimeters to compare different components and structures. This is particularly important in fields such as civil and mechanical engineering, where maintaining proportionality can affect the functionality and safety of structures.
- Geometric Analysis:
In geometry, the ratio of perimeters helps in comparing similar shapes and understanding their properties. For example, when analyzing similar triangles, the ratio of their perimeters is equal to the ratio of their corresponding sides, providing insights into their geometric relationships.
- Art and Design:
Artists and designers use the ratio of perimeters to create aesthetically pleasing compositions. By maintaining proportional relationships, they ensure that their designs are balanced and harmonious.
- Scale Models:
Creating scale models of various objects, such as vehicles, furniture, and landscapes, involves using the ratio of perimeters to ensure that all parts of the model are proportionally accurate.
- Real-World Problem Solving:
In everyday situations, the ratio of perimeters can be used to solve problems related to resizing objects, such as resizing photographs, maps, and blueprints while maintaining their proportions.
Understanding the ratio of perimeters and its applications helps in various fields by providing a fundamental tool for comparing, scaling, and analyzing shapes and structures.
Applications of Ratio of Perimeters
The ratio of perimeters has various practical applications in geometry, engineering, architecture, and everyday problem-solving. Understanding this concept allows for better design, analysis, and scaling of objects and structures. Here are some key applications:
- Architecture and Design:
In architecture, the ratio of perimeters is crucial for scaling models of buildings. Architects use this ratio to create accurate scale models that preserve the proportions of the original structure. This helps in visualizing the final product and ensuring structural integrity.
- Engineering:
Engineers often use the ratio of perimeters to compare different components and structures. This is particularly important in fields such as civil and mechanical engineering, where maintaining proportionality can affect the functionality and safety of structures.
- Geometric Analysis:
In geometry, the ratio of perimeters helps in comparing similar shapes and understanding their properties. For example, when analyzing similar triangles, the ratio of their perimeters is equal to the ratio of their corresponding sides, providing insights into their geometric relationships.
- Art and Design:
Artists and designers use the ratio of perimeters to create aesthetically pleasing compositions. By maintaining proportional relationships, they ensure that their designs are balanced and harmonious.
- Scale Models:
Creating scale models of various objects, such as vehicles, furniture, and landscapes, involves using the ratio of perimeters to ensure that all parts of the model are proportionally accurate.
- Real-World Problem Solving:
In everyday situations, the ratio of perimeters can be used to solve problems related to resizing objects, such as resizing photographs, maps, and blueprints while maintaining their proportions.
Understanding the ratio of perimeters and its applications helps in various fields by providing a fundamental tool for comparing, scaling, and analyzing shapes and structures.
Examples of Ratio of Perimeters
The ratio of perimeters can be observed in various geometric shapes and real-world scenarios. Here are some detailed examples:
- Example 1: Squares
Consider two squares where the side length of the first square is 3 units and the side length of the second square is 6 units.
- Calculate the perimeter of the first square:
- Calculate the perimeter of the second square:
- Calculate the ratio of perimeters:
The ratio of the perimeters of the two squares is 0.5, indicating that the perimeter of the smaller square is half that of the larger square.
- Example 2: Rectangles
Consider two rectangles, where the dimensions of the first rectangle are 4 units by 6 units, and the dimensions of the second rectangle are 8 units by 12 units.
- Calculate the perimeter of the first rectangle:
- Calculate the perimeter of the second rectangle:
- Calculate the ratio of perimeters:
The ratio of the perimeters of the two rectangles is 0.5, showing that the perimeter of the smaller rectangle is half that of the larger rectangle.
- Example 3: Circles
Consider two circles where the radius of the first circle is 2 units and the radius of the second circle is 4 units.
- Calculate the circumference of the first circle:
- Calculate the circumference of the second circle:
- Calculate the ratio of perimeters:
The ratio of the circumferences of the two circles is 0.5, indicating that the circumference of the smaller circle is half that of the larger circle.
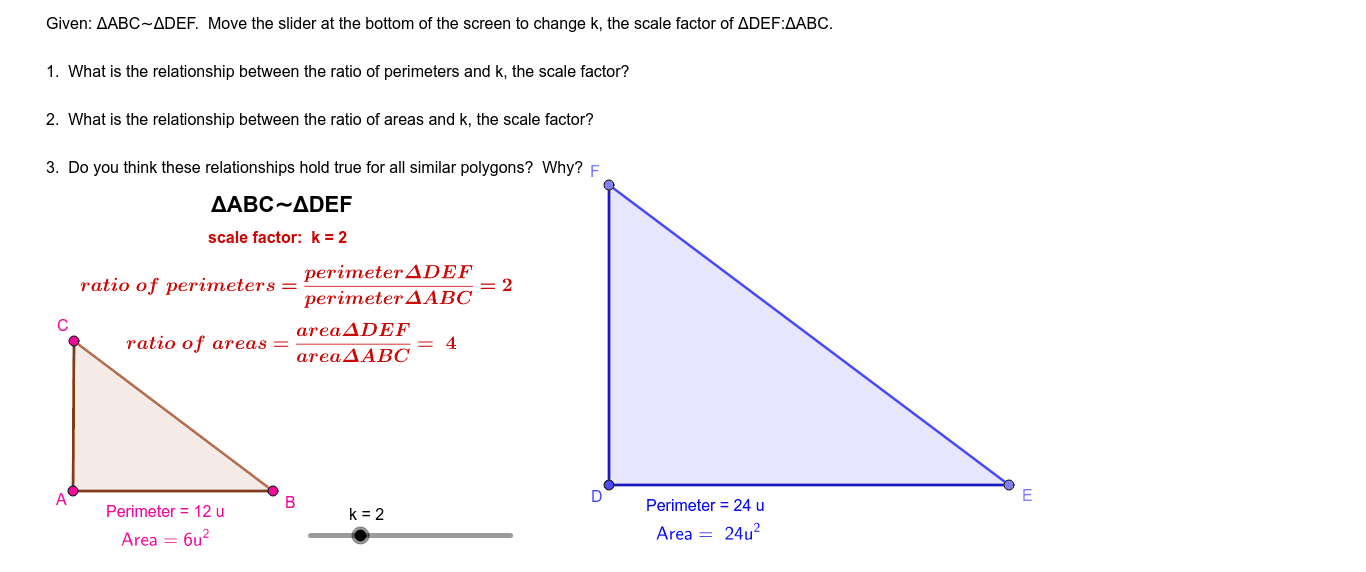
Examples of Ratio of Perimeters
The ratio of perimeters can be observed in various geometric shapes and real-world scenarios. Here are some detailed examples:
- Example 1: Squares
Consider two squares where the side length of the first square is 3 units and the side length of the second square is 6 units.
- Calculate the perimeter of the first square:
- Calculate the perimeter of the second square:
- Calculate the ratio of perimeters:
The ratio of the perimeters of the two squares is 0.5, indicating that the perimeter of the smaller square is half that of the larger square.
- Example 2: Rectangles
Consider two rectangles, where the dimensions of the first rectangle are 4 units by 6 units, and the dimensions of the second rectangle are 8 units by 12 units.
- Calculate the perimeter of the first rectangle:
- Calculate the perimeter of the second rectangle:
- Calculate the ratio of perimeters:
The ratio of the perimeters of the two rectangles is 0.5, showing that the perimeter of the smaller rectangle is half that of the larger rectangle.
- Example 3: Circles
Consider two circles where the radius of the first circle is 2 units and the radius of the second circle is 4 units.
- Calculate the circumference of the first circle:
- Calculate the circumference of the second circle:
- Calculate the ratio of perimeters:
The ratio of the circumferences of the two circles is 0.5, indicating that the circumference of the smaller circle is half that of the larger circle.

Ratio of Perimeters in Similar Shapes
When dealing with similar shapes, understanding the ratio of perimeters is crucial. Similar shapes are geometric figures that have the same shape but different sizes, and their corresponding angles are equal while their corresponding sides are proportional. Here’s a step-by-step explanation of the ratio of perimeters in similar shapes:
- Identify Corresponding Sides:
First, identify the corresponding sides of the similar shapes. These are the sides that are proportional to each other.
- Calculate the Side Length Ratio:
Next, calculate the ratio of the corresponding side lengths. For example, if two similar triangles have corresponding sides of lengths 3 units and 6 units, the side length ratio is:
- Apply the Side Length Ratio to Perimeters:
For similar shapes, the ratio of the perimeters is equal to the ratio of the corresponding side lengths. Therefore, if the ratio of the side lengths is 0.5, the ratio of the perimeters is also 0.5.
- Example Calculation:
Consider two similar rectangles where the lengths of the corresponding sides are 4 units and 8 units respectively. If the perimeter of the smaller rectangle is calculated as follows:
Then the perimeter of the larger rectangle, considering the side length ratio of 0.5, will be:
So the ratio of the perimeters is:
- General Formula:
The general formula for the ratio of perimeters of similar shapes is:
Understanding the ratio of perimeters in similar shapes provides valuable insights into the properties and scaling of geometric figures, facilitating various applications in mathematics, engineering, and design.
Ratio of Perimeters in Similar Shapes
When dealing with similar shapes, understanding the ratio of perimeters is crucial. Similar shapes are geometric figures that have the same shape but different sizes, and their corresponding angles are equal while their corresponding sides are proportional. Here’s a step-by-step explanation of the ratio of perimeters in similar shapes:
- Identify Corresponding Sides:
First, identify the corresponding sides of the similar shapes. These are the sides that are proportional to each other.
- Calculate the Side Length Ratio:
Next, calculate the ratio of the corresponding side lengths. For example, if two similar triangles have corresponding sides of lengths 3 units and 6 units, the side length ratio is:
- Apply the Side Length Ratio to Perimeters:
For similar shapes, the ratio of the perimeters is equal to the ratio of the corresponding side lengths. Therefore, if the ratio of the side lengths is 0.5, the ratio of the perimeters is also 0.5.
- Example Calculation:
Consider two similar rectangles where the lengths of the corresponding sides are 4 units and 8 units respectively. If the perimeter of the smaller rectangle is calculated as follows:
Then the perimeter of the larger rectangle, considering the side length ratio of 0.5, will be:
So the ratio of the perimeters is:
- General Formula:
The general formula for the ratio of perimeters of similar shapes is:
Understanding the ratio of perimeters in similar shapes provides valuable insights into the properties and scaling of geometric figures, facilitating various applications in mathematics, engineering, and design.
Scaling Figures and Perimeter Ratios
When scaling geometric figures, understanding the relationship between the scale factor and the perimeter is crucial. The ratio of the perimeters of similar figures is directly proportional to the scale factor applied to their corresponding dimensions.
Let's delve into the concept step by step:
-
Definition: The scale factor is a number which scales, or multiplies, some quantity. In the context of geometric figures, it refers to the factor by which all dimensions of a shape are enlarged or reduced.
-
Perimeter Ratio: If two figures are similar, the ratio of their perimeters is equal to the ratio of their corresponding side lengths. Mathematically, if a figure is scaled by a factor of \( k \), then the perimeter of the scaled figure is \( k \) times the perimeter of the original figure.
For example, if the scale factor is 2, the perimeter of the scaled figure will be twice the perimeter of the original figure.
-
Mathematical Representation: If \( P_1 \) is the perimeter of the original figure and \( P_2 \) is the perimeter of the scaled figure, and if the scale factor is \( k \), then:
\[
P_2 = k \cdot P_1
\] -
Example Calculation:
- Consider a rectangle with a perimeter of 20 units.
- If the rectangle is scaled by a factor of 3, the new perimeter will be:
\[
P_2 = 3 \cdot 20 = 60 \text{ units}
\]
This principle applies universally to all geometric shapes. When scaling any shape, be it a triangle, square, or more complex polygon, the perimeter scales linearly with the scale factor.
Below is a table summarizing the effect of different scale factors on the perimeter:
| Original Perimeter (units) | Scale Factor | New Perimeter (units) |
|---|---|---|
| 10 | 2 | 20 |
| 15 | 0.5 | 7.5 |
| 25 | 4 | 100 |
Understanding this concept is particularly useful in real-world applications where resizing of objects is required, such as in map scaling, model building, and computer graphics.
Scaling Figures and Perimeter Ratios
When scaling geometric figures, understanding the relationship between the scale factor and the perimeter is crucial. The ratio of the perimeters of similar figures is directly proportional to the scale factor applied to their corresponding dimensions.
Let's delve into the concept step by step:
-
Definition: The scale factor is a number which scales, or multiplies, some quantity. In the context of geometric figures, it refers to the factor by which all dimensions of a shape are enlarged or reduced.
-
Perimeter Ratio: If two figures are similar, the ratio of their perimeters is equal to the ratio of their corresponding side lengths. Mathematically, if a figure is scaled by a factor of \( k \), then the perimeter of the scaled figure is \( k \) times the perimeter of the original figure.
For example, if the scale factor is 2, the perimeter of the scaled figure will be twice the perimeter of the original figure.
-
Mathematical Representation: If \( P_1 \) is the perimeter of the original figure and \( P_2 \) is the perimeter of the scaled figure, and if the scale factor is \( k \), then:
\[
P_2 = k \cdot P_1
\] -
Example Calculation:
- Consider a rectangle with a perimeter of 20 units.
- If the rectangle is scaled by a factor of 3, the new perimeter will be:
\[
P_2 = 3 \cdot 20 = 60 \text{ units}
\]
This principle applies universally to all geometric shapes. When scaling any shape, be it a triangle, square, or more complex polygon, the perimeter scales linearly with the scale factor.
Below is a table summarizing the effect of different scale factors on the perimeter:
| Original Perimeter (units) | Scale Factor | New Perimeter (units) |
|---|---|---|
| 10 | 2 | 20 |
| 15 | 0.5 | 7.5 |
| 25 | 4 | 100 |
Understanding this concept is particularly useful in real-world applications where resizing of objects is required, such as in map scaling, model building, and computer graphics.
Practical Uses in Real-World Applications
The ratio of perimeters is a fundamental concept that finds numerous applications in various real-world scenarios. Below are some of the practical uses:
-
Urban Planning and Architecture:
Architects and urban planners use the ratio of perimeters to design scalable models of buildings and urban layouts. By maintaining the ratio, they ensure that their designs are proportionate and aesthetically pleasing.
-
Manufacturing and Engineering:
In manufacturing, especially in the creation of parts and components, maintaining the ratio of perimeters is crucial for ensuring compatibility and functionality. Engineers often scale models while keeping perimeter ratios constant to test prototypes.
-
Cartography and Geography:
Cartographers use the ratio of perimeters when creating maps to accurately represent the boundaries of geographical areas. This helps in maintaining the correct proportions of different regions on the map.
-
Art and Design:
Artists and designers frequently use the concept of perimeter ratios to create visually balanced and harmonious works. This is especially important in graphic design, where the scaling of different elements must preserve the overall look and feel.
-
Agriculture:
Farmers and agricultural planners use perimeter ratios to plan the layout of fields and irrigation systems. This ensures efficient use of space and resources, promoting better crop yields and sustainable practices.
-
Sports:
In sports, especially in track and field events, maintaining the ratio of perimeters of different track layouts ensures fairness and consistency in competitions. This helps in standardizing the dimensions across various venues.
Understanding and applying the ratio of perimeters in these fields enhances precision, efficiency, and aesthetic quality, demonstrating its significance in practical applications.
Practical Uses in Real-World Applications
The ratio of perimeters is a fundamental concept that finds numerous applications in various real-world scenarios. Below are some of the practical uses:
-
Urban Planning and Architecture:
Architects and urban planners use the ratio of perimeters to design scalable models of buildings and urban layouts. By maintaining the ratio, they ensure that their designs are proportionate and aesthetically pleasing.
-
Manufacturing and Engineering:
In manufacturing, especially in the creation of parts and components, maintaining the ratio of perimeters is crucial for ensuring compatibility and functionality. Engineers often scale models while keeping perimeter ratios constant to test prototypes.
-
Cartography and Geography:
Cartographers use the ratio of perimeters when creating maps to accurately represent the boundaries of geographical areas. This helps in maintaining the correct proportions of different regions on the map.
-
Art and Design:
Artists and designers frequently use the concept of perimeter ratios to create visually balanced and harmonious works. This is especially important in graphic design, where the scaling of different elements must preserve the overall look and feel.
-
Agriculture:
Farmers and agricultural planners use perimeter ratios to plan the layout of fields and irrigation systems. This ensures efficient use of space and resources, promoting better crop yields and sustainable practices.
-
Sports:
In sports, especially in track and field events, maintaining the ratio of perimeters of different track layouts ensures fairness and consistency in competitions. This helps in standardizing the dimensions across various venues.
Understanding and applying the ratio of perimeters in these fields enhances precision, efficiency, and aesthetic quality, demonstrating its significance in practical applications.
Comparison of Different Geometric Shapes
The ratio of perimeters is a valuable concept when comparing different geometric shapes. This section explores the perimeter ratios of various common geometric shapes and their implications.
Triangles
The perimeter of a triangle is the sum of the lengths of its three sides:
\[
\text{Perimeter} = a + b + c
\]
Comparing the perimeters of two triangles with sides \(a_1, b_1, c_1\) and \(a_2, b_2, c_2\), respectively, we have:
\[
\text{Ratio of Perimeters} = \frac{a_1 + b_1 + c_1}{a_2 + b_2 + c_2}
\]
Quadrilaterals
For quadrilaterals, such as rectangles and squares, the perimeter is calculated differently:
- Rectangle: \[ \text{Perimeter} = 2 \times (\text{Length} + \text{Width}) \]
- Square: \[ \text{Perimeter} = 4 \times \text{Side} \]
Circles
The perimeter of a circle, known as the circumference, is given by:
\[
\text{Circumference} = 2\pi r
\]
Comparing the perimeters of two circles with radii \(r_1\) and \(r_2\), respectively, the ratio is:
\[
\text{Ratio of Circumferences} = \frac{2\pi r_1}{2\pi r_2} = \frac{r_1}{r_2}
\]
Regular Polygons
For regular polygons, where all sides are equal, the perimeter can be found using:
\[
\text{Perimeter} = n \times \text{Side}
\]
where \(n\) is the number of sides. Comparing the perimeters of two regular polygons with side lengths \(s_1\) and \(s_2\), and the same number of sides \(n\), the ratio is:
\[
\text{Ratio of Perimeters} = \frac{n \times s_1}{n \times s_2} = \frac{s_1}{s_2}
\]
Applications
Understanding these ratios is crucial in various fields such as architecture, engineering, and design, where comparing different shapes and scaling models are common practices. For instance, when creating scale models, maintaining the ratio of perimeters ensures proportionality and accuracy in the representation of structures.
In summary, the ratio of perimeters provides a straightforward way to compare different geometric shapes, offering insights into their relative sizes and aiding in practical applications where size and scale are important considerations.

Comparison of Different Geometric Shapes
The ratio of perimeters is a valuable concept when comparing different geometric shapes. This section explores the perimeter ratios of various common geometric shapes and their implications.
Triangles
The perimeter of a triangle is the sum of the lengths of its three sides:
\[
\text{Perimeter} = a + b + c
\]
Comparing the perimeters of two triangles with sides \(a_1, b_1, c_1\) and \(a_2, b_2, c_2\), respectively, we have:
\[
\text{Ratio of Perimeters} = \frac{a_1 + b_1 + c_1}{a_2 + b_2 + c_2}
\]
Quadrilaterals
For quadrilaterals, such as rectangles and squares, the perimeter is calculated differently:
- Rectangle: \[ \text{Perimeter} = 2 \times (\text{Length} + \text{Width}) \]
- Square: \[ \text{Perimeter} = 4 \times \text{Side} \]
Circles
The perimeter of a circle, known as the circumference, is given by:
\[
\text{Circumference} = 2\pi r
\]
Comparing the perimeters of two circles with radii \(r_1\) and \(r_2\), respectively, the ratio is:
\[
\text{Ratio of Circumferences} = \frac{2\pi r_1}{2\pi r_2} = \frac{r_1}{r_2}
\]
Regular Polygons
For regular polygons, where all sides are equal, the perimeter can be found using:
\[
\text{Perimeter} = n \times \text{Side}
\]
where \(n\) is the number of sides. Comparing the perimeters of two regular polygons with side lengths \(s_1\) and \(s_2\), and the same number of sides \(n\), the ratio is:
\[
\text{Ratio of Perimeters} = \frac{n \times s_1}{n \times s_2} = \frac{s_1}{s_2}
\]
Applications
Understanding these ratios is crucial in various fields such as architecture, engineering, and design, where comparing different shapes and scaling models are common practices. For instance, when creating scale models, maintaining the ratio of perimeters ensures proportionality and accuracy in the representation of structures.
In summary, the ratio of perimeters provides a straightforward way to compare different geometric shapes, offering insights into their relative sizes and aiding in practical applications where size and scale are important considerations.

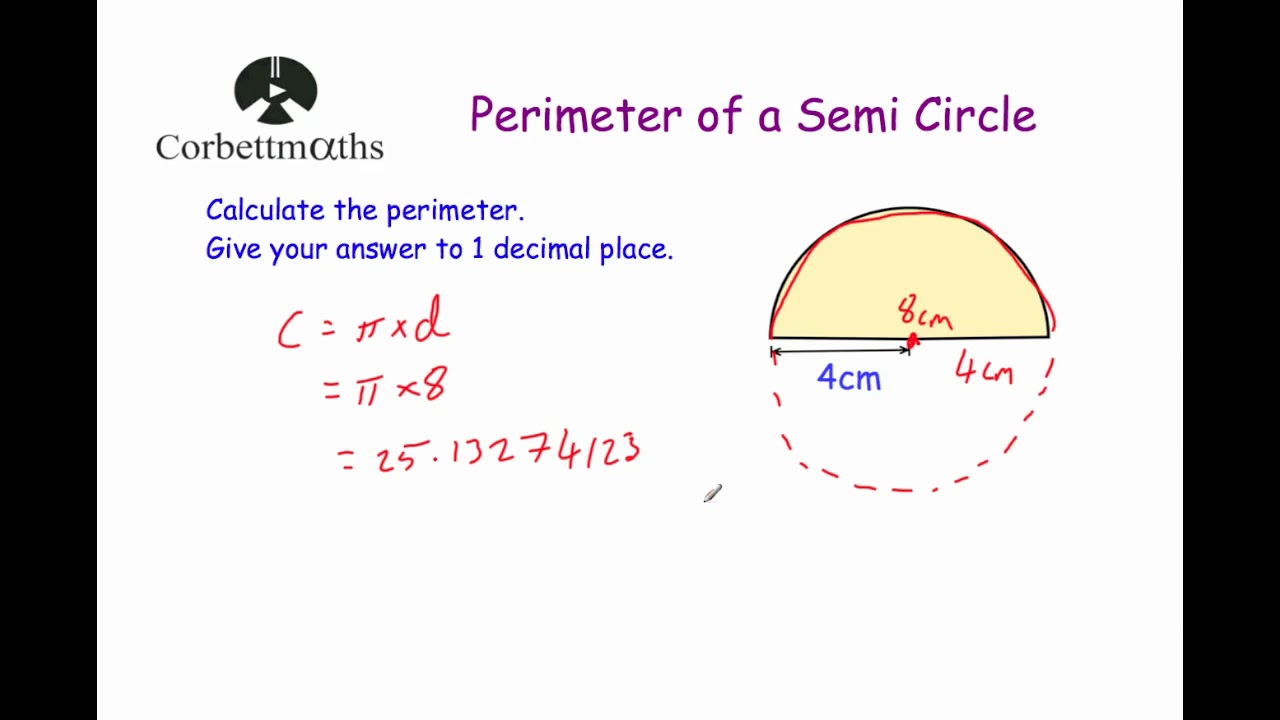
Ratio of Perimeters in Complex Figures
The concept of the ratio of perimeters can be extended beyond simple geometric shapes to more complex figures. Understanding the perimeter ratio in complex figures involves breaking down the figure into simpler components or using known geometric properties to establish relationships.
Here are some steps and considerations for analyzing the ratio of perimeters in complex figures:
-
Decompose the Figure: Start by decomposing the complex figure into simpler shapes (e.g., triangles, rectangles, circles). Calculate the perimeter of each simpler shape.
-
Identify Similar Shapes: If the complex figure contains similar shapes, use the properties of similar figures. For similar shapes, the ratio of their perimeters is the same as the ratio of their corresponding sides.
\[ \text{Perimeter Ratio} = \frac{\text{Side Length of Shape A}}{\text{Side Length of Shape B}} \]
-
Summation of Perimeters: Sum the perimeters of all the individual shapes to find the total perimeter of the complex figure. If comparing two complex figures, sum their respective perimeters.
-
Apply Known Ratios: For shapes where the scale factor is known, apply the perimeter ratio directly. For example, if two figures are similar with a scale factor of \(\frac{m}{n}\), the ratio of their perimeters will also be \(\frac{m}{n}\).
Consider the following example to illustrate these steps:
Example:
Suppose we have two complex figures composed of a rectangle and a semicircle. The first complex figure (Figure 1) has a rectangle of length 10 units and width 5 units, with a semicircle of radius 5 units attached to one side. The second complex figure (Figure 2) is similar but scaled up by a factor of 2.
- Calculate the perimeter of the rectangle in Figure 1: \(P_{\text{rect}} = 2(10) + 2(5) = 30\) units.
- Calculate the perimeter of the semicircle in Figure 1: \(P_{\text{semi}} = \pi \times 5 = 15.7\) units (approximated).
- Total perimeter of Figure 1: \(P_{\text{total 1}} = 30 + 15.7 = 45.7\) units.
- Since Figure 2 is scaled up by a factor of 2, the side lengths and radius double, thus the perimeter ratio between Figure 1 and Figure 2 is 1:2.
- Calculate the perimeter of Figure 2 by scaling up: \(P_{\text{total 2}} = 2 \times 45.7 = 91.4\) units.
In conclusion, by understanding the geometric properties and using decomposition, you can effectively determine and compare the perimeters of complex figures.
Ratio of Perimeters in Complex Figures
The concept of the ratio of perimeters can be extended beyond simple geometric shapes to more complex figures. Understanding the perimeter ratio in complex figures involves breaking down the figure into simpler components or using known geometric properties to establish relationships.
Here are some steps and considerations for analyzing the ratio of perimeters in complex figures:
-
Decompose the Figure: Start by decomposing the complex figure into simpler shapes (e.g., triangles, rectangles, circles). Calculate the perimeter of each simpler shape.
-
Identify Similar Shapes: If the complex figure contains similar shapes, use the properties of similar figures. For similar shapes, the ratio of their perimeters is the same as the ratio of their corresponding sides.
\[ \text{Perimeter Ratio} = \frac{\text{Side Length of Shape A}}{\text{Side Length of Shape B}} \]
-
Summation of Perimeters: Sum the perimeters of all the individual shapes to find the total perimeter of the complex figure. If comparing two complex figures, sum their respective perimeters.
-
Apply Known Ratios: For shapes where the scale factor is known, apply the perimeter ratio directly. For example, if two figures are similar with a scale factor of \(\frac{m}{n}\), the ratio of their perimeters will also be \(\frac{m}{n}\).
Consider the following example to illustrate these steps:
Example:
Suppose we have two complex figures composed of a rectangle and a semicircle. The first complex figure (Figure 1) has a rectangle of length 10 units and width 5 units, with a semicircle of radius 5 units attached to one side. The second complex figure (Figure 2) is similar but scaled up by a factor of 2.
- Calculate the perimeter of the rectangle in Figure 1: \(P_{\text{rect}} = 2(10) + 2(5) = 30\) units.
- Calculate the perimeter of the semicircle in Figure 1: \(P_{\text{semi}} = \pi \times 5 = 15.7\) units (approximated).
- Total perimeter of Figure 1: \(P_{\text{total 1}} = 30 + 15.7 = 45.7\) units.
- Since Figure 2 is scaled up by a factor of 2, the side lengths and radius double, thus the perimeter ratio between Figure 1 and Figure 2 is 1:2.
- Calculate the perimeter of Figure 2 by scaling up: \(P_{\text{total 2}} = 2 \times 45.7 = 91.4\) units.
In conclusion, by understanding the geometric properties and using decomposition, you can effectively determine and compare the perimeters of complex figures.
Làm thế nào để tìm tỷ lệ chu vi của hai đa giác: Bài học Toán & Vật lý
READ MORE:
Tỷ lệ Chu vi / Tỷ lệ Diện tích