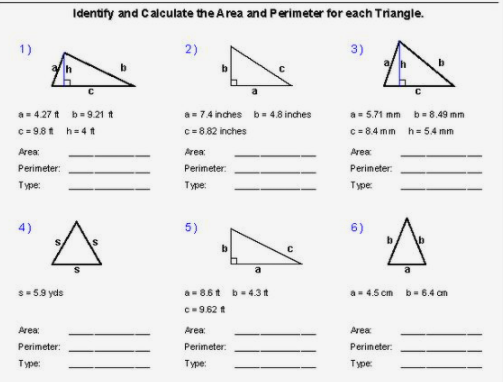
Topic semi circle perimeter: Understanding the semi-circle perimeter is crucial for various mathematical and practical applications. This comprehensive guide will walk you through the definition, formula, step-by-step calculations, and real-world uses of the semi-circle perimeter, ensuring you grasp this essential concept with ease and confidence.
Table of Content
- Perimeter of a Semi-Circle
- Perimeter of a Semi-Circle
- Introduction to Semi-Circle Perimeter
- Introduction to Semi-Circle Perimeter
- Understanding Semi-Circle Geometry
- Understanding Semi-Circle Geometry
- Perimeter of a Semi-Circle: Definition and Formula
- Perimeter of a Semi-Circle: Definition and Formula
- Derivation of the Perimeter Formula
- Derivation of the Perimeter Formula
- Step-by-Step Calculation of Semi-Circle Perimeter
- Step-by-Step Calculation of Semi-Circle Perimeter
- Examples of Perimeter Calculation
- Examples of Perimeter Calculation
- Practical Applications of Semi-Circle Perimeter
- Practical Applications of Semi-Circle Perimeter
- Common Mistakes and How to Avoid Them
- Common Mistakes and How to Avoid Them
- Advanced Topics: Semi-Circle in Different Coordinate Systems
- Advanced Topics: Semi-Circle in Different Coordinate Systems
- Summary and Key Takeaways
- Summary and Key Takeaways
- Frequently Asked Questions (FAQs)
- Frequently Asked Questions (FAQs)
- Further Reading and Resources
- Further Reading and Resources
- YOUTUBE: Hướng dẫn chi tiết cách tính chu vi nửa hình tròn, giải thích công thức và ví dụ minh họa.
Perimeter of a Semi-Circle
The perimeter of a semi-circle is the total distance around the semi-circle, which includes the curved part (half the circumference of a full circle) and the diameter.
Formula
The formula to calculate the perimeter \( P \) of a semi-circle with radius \( r \) is:
$$ P = \pi r + 2r $$
Where:
- \( \pi \) is approximately 3.14159
- \( r \) is the radius of the semi-circle
Steps to Calculate the Perimeter
- Calculate the circumference of the full circle: \( C = 2\pi r \).
- Divide the circumference by 2 to get the semi-circle's curved edge: \( \frac{1}{2} \times 2\pi r = \pi r \).
- Add the diameter of the circle: \( 2r \).
- Combine the two results to get the perimeter of the semi-circle: \( P = \pi r + 2r \).
Example Calculation
For a semi-circle with a radius of 5 units:
- Curved part of the semi-circle: \( \pi \times 5 = 15.70795 \) units
- Diameter: \( 2 \times 5 = 10 \) units
- Perimeter: \( 15.70795 + 10 = 25.70795 \) units
Therefore, the perimeter of a semi-circle with a radius of 5 units is approximately 25.71 units.

READ MORE:
Perimeter of a Semi-Circle
The perimeter of a semi-circle is the total distance around the semi-circle, which includes the curved part (half the circumference of a full circle) and the diameter.
Formula
The formula to calculate the perimeter \( P \) of a semi-circle with radius \( r \) is:
$$ P = \pi r + 2r $$
Where:
- \( \pi \) is approximately 3.14159
- \( r \) is the radius of the semi-circle
Steps to Calculate the Perimeter
- Calculate the circumference of the full circle: \( C = 2\pi r \).
- Divide the circumference by 2 to get the semi-circle's curved edge: \( \frac{1}{2} \times 2\pi r = \pi r \).
- Add the diameter of the circle: \( 2r \).
- Combine the two results to get the perimeter of the semi-circle: \( P = \pi r + 2r \).
Example Calculation
For a semi-circle with a radius of 5 units:
- Curved part of the semi-circle: \( \pi \times 5 = 15.70795 \) units
- Diameter: \( 2 \times 5 = 10 \) units
- Perimeter: \( 15.70795 + 10 = 25.70795 \) units
Therefore, the perimeter of a semi-circle with a radius of 5 units is approximately 25.71 units.

Introduction to Semi-Circle Perimeter
The perimeter of a semi-circle is an important concept in geometry, combining the length of the curved edge with the straight line segment (diameter) that forms its base. It is essential for understanding various geometric properties and practical applications.
To grasp the semi-circle perimeter, consider the following points:
- A semi-circle is half of a full circle.
- The perimeter involves both the curved part (half the circumference of the full circle) and the diameter.
- The formula to calculate the perimeter is straightforward and uses basic elements of circle geometry.
The formula to determine the perimeter \( P \) of a semi-circle with radius \( r \) is:
$$ P = \pi r + 2r $$
Where:
- \( \pi \) is the mathematical constant Pi, approximately equal to 3.14159.
- \( r \) is the radius of the semi-circle.
Let's break down the calculation into simple steps:
- Calculate the circumference of the full circle using \( 2\pi r \).
- Divide this circumference by 2 to find the length of the curved edge of the semi-circle: \( \pi r \).
- Add the diameter (which is twice the radius): \( 2r \).
- Combine these values to get the total perimeter: \( P = \pi r + 2r \).
For instance, if the radius of a semi-circle is 4 units:
- The curved part of the semi-circle would be \( \pi \times 4 = 12.566 \) units.
- The diameter would be \( 2 \times 4 = 8 \) units.
- Therefore, the total perimeter is \( 12.566 + 8 = 20.566 \) units.
Understanding the perimeter of a semi-circle allows for deeper insights into various geometrical problems and practical scenarios, such as designing arches, calculating distances, and more.
Introduction to Semi-Circle Perimeter
The perimeter of a semi-circle is an important concept in geometry, combining the length of the curved edge with the straight line segment (diameter) that forms its base. It is essential for understanding various geometric properties and practical applications.
To grasp the semi-circle perimeter, consider the following points:
- A semi-circle is half of a full circle.
- The perimeter involves both the curved part (half the circumference of the full circle) and the diameter.
- The formula to calculate the perimeter is straightforward and uses basic elements of circle geometry.
The formula to determine the perimeter \( P \) of a semi-circle with radius \( r \) is:
$$ P = \pi r + 2r $$
Where:
- \( \pi \) is the mathematical constant Pi, approximately equal to 3.14159.
- \( r \) is the radius of the semi-circle.
Let's break down the calculation into simple steps:
- Calculate the circumference of the full circle using \( 2\pi r \).
- Divide this circumference by 2 to find the length of the curved edge of the semi-circle: \( \pi r \).
- Add the diameter (which is twice the radius): \( 2r \).
- Combine these values to get the total perimeter: \( P = \pi r + 2r \).
For instance, if the radius of a semi-circle is 4 units:
- The curved part of the semi-circle would be \( \pi \times 4 = 12.566 \) units.
- The diameter would be \( 2 \times 4 = 8 \) units.
- Therefore, the total perimeter is \( 12.566 + 8 = 20.566 \) units.
Understanding the perimeter of a semi-circle allows for deeper insights into various geometrical problems and practical scenarios, such as designing arches, calculating distances, and more.
Understanding Semi-Circle Geometry
A semi-circle is a two-dimensional geometric shape that represents half of a full circle. Understanding its geometry involves knowing its properties, components, and how to calculate various measurements related to it.
Key characteristics of a semi-circle include:
- It is formed by cutting a full circle along its diameter.
- The straight edge of a semi-circle is its diameter, which is twice the length of its radius.
- The curved edge is half the circumference of the full circle.
- A semi-circle has one line of symmetry along its diameter.
To delve deeper into the geometry of a semi-circle, consider the following essential elements:
- Radius (\( r \)): The distance from the center of the full circle to any point on its boundary. In a semi-circle, this remains the same.
- Diameter (\( d \)): The longest distance across the semi-circle, passing through its center. It is given by \( d = 2r \).
- Curved Edge: This is half of the full circle's circumference. The circumference of a full circle is \( 2\pi r \), so the curved edge of a semi-circle is \( \pi r \).
The area and perimeter of a semi-circle can be calculated using the following formulas:
- Area: The area of a semi-circle is half the area of a full circle. The formula is: $$ A = \frac{1}{2} \pi r^2 $$
- Perimeter: The perimeter of a semi-circle includes the curved edge and the diameter. The formula is: $$ P = \pi r + 2r $$
For a semi-circle with a radius of \( r = 3 \) units:
- The diameter \( d \) would be \( 2 \times 3 = 6 \) units.
- The curved edge would be \( \pi \times 3 = 9.42 \) units.
- The perimeter would be \( 9.42 + 6 = 15.42 \) units.
- The area would be: $$ A = \frac{1}{2} \pi (3)^2 = \frac{1}{2} \pi \times 9 = 14.13 \text{ square units} $$
By understanding these fundamental aspects of semi-circle geometry, one can apply this knowledge to solve various geometric problems and practical applications, such as designing semi-circular structures, calculating areas for landscaping, and more.
Understanding Semi-Circle Geometry
A semi-circle is a two-dimensional geometric shape that represents half of a full circle. Understanding its geometry involves knowing its properties, components, and how to calculate various measurements related to it.
Key characteristics of a semi-circle include:
- It is formed by cutting a full circle along its diameter.
- The straight edge of a semi-circle is its diameter, which is twice the length of its radius.
- The curved edge is half the circumference of the full circle.
- A semi-circle has one line of symmetry along its diameter.
To delve deeper into the geometry of a semi-circle, consider the following essential elements:
- Radius (\( r \)): The distance from the center of the full circle to any point on its boundary. In a semi-circle, this remains the same.
- Diameter (\( d \)): The longest distance across the semi-circle, passing through its center. It is given by \( d = 2r \).
- Curved Edge: This is half of the full circle's circumference. The circumference of a full circle is \( 2\pi r \), so the curved edge of a semi-circle is \( \pi r \).
The area and perimeter of a semi-circle can be calculated using the following formulas:
- Area: The area of a semi-circle is half the area of a full circle. The formula is: $$ A = \frac{1}{2} \pi r^2 $$
- Perimeter: The perimeter of a semi-circle includes the curved edge and the diameter. The formula is: $$ P = \pi r + 2r $$
For a semi-circle with a radius of \( r = 3 \) units:
- The diameter \( d \) would be \( 2 \times 3 = 6 \) units.
- The curved edge would be \( \pi \times 3 = 9.42 \) units.
- The perimeter would be \( 9.42 + 6 = 15.42 \) units.
- The area would be: $$ A = \frac{1}{2} \pi (3)^2 = \frac{1}{2} \pi \times 9 = 14.13 \text{ square units} $$
By understanding these fundamental aspects of semi-circle geometry, one can apply this knowledge to solve various geometric problems and practical applications, such as designing semi-circular structures, calculating areas for landscaping, and more.
Perimeter of a Semi-Circle: Definition and Formula
The perimeter of a semi-circle is the total distance around the shape, which includes the length of the curved edge (half the circumference of a full circle) and the diameter. Understanding and calculating this perimeter is fundamental in geometry.
Definition: The perimeter of a semi-circle is the sum of the length of the semi-circular arc and the diameter of the semi-circle.
Formula: The formula to calculate the perimeter \( P \) of a semi-circle with radius \( r \) is:
$$ P = \pi r + 2r $$
Where:
- \( \pi \) (Pi) is a constant approximately equal to 3.14159.
- \( r \) is the radius of the semi-circle.
To understand the formula better, let's break down the calculation into steps:
- Calculate the circumference of the full circle: The circumference \( C \) of a full circle is given by \( 2\pi r \).
- Find the length of the curved edge: Since a semi-circle is half of a full circle, the length of the curved edge is \( \frac{1}{2} \times 2\pi r = \pi r \).
- Add the diameter: The diameter \( d \) is twice the radius, so \( d = 2r \).
- Sum these two lengths: The total perimeter \( P \) is \( \pi r + 2r \).
For a semi-circle with a radius of 5 units, let's calculate the perimeter:
- Curved edge: \( \pi \times 5 = 15.70795 \) units
- Diameter: \( 2 \times 5 = 10 \) units
- Total perimeter: \( 15.70795 + 10 = 25.70795 \) units
Thus, the perimeter of a semi-circle with a radius of 5 units is approximately 25.71 units.
By understanding this formula and calculation method, you can easily determine the perimeter of any semi-circle, aiding in various geometric and real-world applications.
Perimeter of a Semi-Circle: Definition and Formula
The perimeter of a semi-circle is the total distance around the shape, which includes the length of the curved edge (half the circumference of a full circle) and the diameter. Understanding and calculating this perimeter is fundamental in geometry.
Definition: The perimeter of a semi-circle is the sum of the length of the semi-circular arc and the diameter of the semi-circle.
Formula: The formula to calculate the perimeter \( P \) of a semi-circle with radius \( r \) is:
$$ P = \pi r + 2r $$
Where:
- \( \pi \) (Pi) is a constant approximately equal to 3.14159.
- \( r \) is the radius of the semi-circle.
To understand the formula better, let's break down the calculation into steps:
- Calculate the circumference of the full circle: The circumference \( C \) of a full circle is given by \( 2\pi r \).
- Find the length of the curved edge: Since a semi-circle is half of a full circle, the length of the curved edge is \( \frac{1}{2} \times 2\pi r = \pi r \).
- Add the diameter: The diameter \( d \) is twice the radius, so \( d = 2r \).
- Sum these two lengths: The total perimeter \( P \) is \( \pi r + 2r \).
For a semi-circle with a radius of 5 units, let's calculate the perimeter:
- Curved edge: \( \pi \times 5 = 15.70795 \) units
- Diameter: \( 2 \times 5 = 10 \) units
- Total perimeter: \( 15.70795 + 10 = 25.70795 \) units
Thus, the perimeter of a semi-circle with a radius of 5 units is approximately 25.71 units.
By understanding this formula and calculation method, you can easily determine the perimeter of any semi-circle, aiding in various geometric and real-world applications.
Derivation of the Perimeter Formula
The perimeter of a semi-circle involves both the curved part (half of the circumference of a full circle) and the straight line segment (diameter). To derive the formula for the perimeter, we will follow these steps:
- Understanding the Circumference of a Full Circle:
The circumference \( C \) of a full circle with radius \( r \) is given by:
$$ C = 2\pi r $$
- Finding the Length of the Curved Edge:
A semi-circle is half of a full circle, so the length of the curved edge \( L \) is:
$$ L = \frac{1}{2} \times 2\pi r = \pi r $$
- Adding the Diameter:
The diameter \( d \) is the straight line segment that forms the base of the semi-circle. It is twice the radius, given by:
$$ d = 2r $$
- Combining the Curved Edge and Diameter:
The total perimeter \( P \) of the semi-circle is the sum of the curved edge and the diameter:
$$ P = \pi r + 2r $$
For example, if the radius of the semi-circle is \( r = 4 \) units:
- Curved edge \( L = \pi \times 4 = 12.566 \) units
- Diameter \( d = 2 \times 4 = 8 \) units
- Total perimeter \( P = 12.566 + 8 = 20.566 \) units
Thus, the derived formula for the perimeter of a semi-circle is:
$$ P = \pi r + 2r $$
This derivation helps us understand the components involved in calculating the perimeter and ensures that the formula is applied correctly for any given radius.
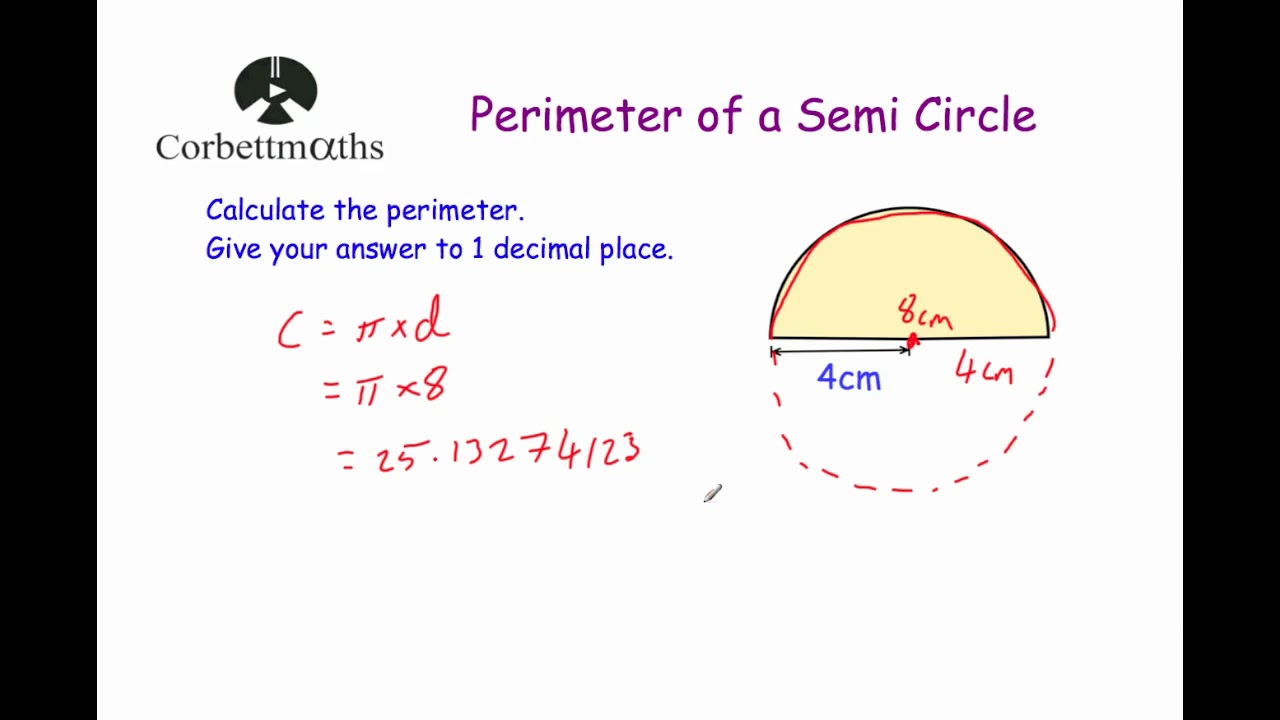
Derivation of the Perimeter Formula
The perimeter of a semi-circle involves both the curved part (half of the circumference of a full circle) and the straight line segment (diameter). To derive the formula for the perimeter, we will follow these steps:
- Understanding the Circumference of a Full Circle:
The circumference \( C \) of a full circle with radius \( r \) is given by:
$$ C = 2\pi r $$
- Finding the Length of the Curved Edge:
A semi-circle is half of a full circle, so the length of the curved edge \( L \) is:
$$ L = \frac{1}{2} \times 2\pi r = \pi r $$
- Adding the Diameter:
The diameter \( d \) is the straight line segment that forms the base of the semi-circle. It is twice the radius, given by:
$$ d = 2r $$
- Combining the Curved Edge and Diameter:
The total perimeter \( P \) of the semi-circle is the sum of the curved edge and the diameter:
$$ P = \pi r + 2r $$
For example, if the radius of the semi-circle is \( r = 4 \) units:
- Curved edge \( L = \pi \times 4 = 12.566 \) units
- Diameter \( d = 2 \times 4 = 8 \) units
- Total perimeter \( P = 12.566 + 8 = 20.566 \) units
Thus, the derived formula for the perimeter of a semi-circle is:
$$ P = \pi r + 2r $$
This derivation helps us understand the components involved in calculating the perimeter and ensures that the formula is applied correctly for any given radius.

Step-by-Step Calculation of Semi-Circle Perimeter
Calculating the perimeter of a semi-circle involves understanding the contributions of both the curved edge and the straight edge (diameter). Here is a detailed, step-by-step guide to help you calculate the perimeter accurately:
- Identify the Radius (\( r \)):
Determine the radius of the semi-circle. The radius is the distance from the center of the full circle to any point on the boundary. Let's denote the radius as \( r \).
- Calculate the Circumference of the Full Circle:
The circumference \( C \) of a full circle is given by the formula:
$$ C = 2\pi r $$
- Determine the Length of the Curved Edge:
Since the semi-circle is half of a full circle, the length of the curved edge \( L \) is half of the circumference:
$$ L = \frac{1}{2} \times 2\pi r = \pi r $$
- Measure the Diameter:
The diameter \( d \) of the semi-circle is twice the radius:
$$ d = 2r $$
- Add the Curved Edge and the Diameter:
The total perimeter \( P \) of the semi-circle is the sum of the curved edge and the diameter:
$$ P = \pi r + 2r $$
Let's go through an example calculation for clarity:
- Step 1: Suppose the radius of the semi-circle is \( r = 6 \) units.
- Step 2: Calculate the circumference of the full circle:
$$ C = 2\pi \times 6 = 12\pi $$
- Step 3: Find the length of the curved edge of the semi-circle:
$$ L = \pi \times 6 = 6\pi \approx 18.85 \text{ units} $$
- Step 4: Determine the diameter of the semi-circle:
$$ d = 2 \times 6 = 12 \text{ units} $$
- Step 5: Calculate the total perimeter:
$$ P = 6\pi + 12 \approx 18.85 + 12 = 30.85 \text{ units} $$
Therefore, the perimeter of a semi-circle with a radius of 6 units is approximately 30.85 units.
By following these steps, you can easily calculate the perimeter of any semi-circle, which is essential for solving various geometric problems and real-life applications.
Step-by-Step Calculation of Semi-Circle Perimeter
Calculating the perimeter of a semi-circle involves understanding the contributions of both the curved edge and the straight edge (diameter). Here is a detailed, step-by-step guide to help you calculate the perimeter accurately:
- Identify the Radius (\( r \)):
Determine the radius of the semi-circle. The radius is the distance from the center of the full circle to any point on the boundary. Let's denote the radius as \( r \).
- Calculate the Circumference of the Full Circle:
The circumference \( C \) of a full circle is given by the formula:
$$ C = 2\pi r $$
- Determine the Length of the Curved Edge:
Since the semi-circle is half of a full circle, the length of the curved edge \( L \) is half of the circumference:
$$ L = \frac{1}{2} \times 2\pi r = \pi r $$
- Measure the Diameter:
The diameter \( d \) of the semi-circle is twice the radius:
$$ d = 2r $$
- Add the Curved Edge and the Diameter:
The total perimeter \( P \) of the semi-circle is the sum of the curved edge and the diameter:
$$ P = \pi r + 2r $$
Let's go through an example calculation for clarity:
- Step 1: Suppose the radius of the semi-circle is \( r = 6 \) units.
- Step 2: Calculate the circumference of the full circle:
$$ C = 2\pi \times 6 = 12\pi $$
- Step 3: Find the length of the curved edge of the semi-circle:
$$ L = \pi \times 6 = 6\pi \approx 18.85 \text{ units} $$
- Step 4: Determine the diameter of the semi-circle:
$$ d = 2 \times 6 = 12 \text{ units} $$
- Step 5: Calculate the total perimeter:
$$ P = 6\pi + 12 \approx 18.85 + 12 = 30.85 \text{ units} $$
Therefore, the perimeter of a semi-circle with a radius of 6 units is approximately 30.85 units.
By following these steps, you can easily calculate the perimeter of any semi-circle, which is essential for solving various geometric problems and real-life applications.
Examples of Perimeter Calculation
To understand the application of the perimeter formula for a semi-circle, let's go through a few detailed examples. These examples will help reinforce the concept and provide clarity on the steps involved in the calculation.
Example 1: Radius of 3 Units
- Identify the Radius:
Let the radius \( r \) be 3 units.
- Calculate the Circumference of the Full Circle:
$$ C = 2\pi r = 2\pi \times 3 = 6\pi \approx 18.85 \text{ units} $$
- Determine the Length of the Curved Edge:
$$ L = \pi r = \pi \times 3 = 3\pi \approx 9.42 \text{ units} $$
- Measure the Diameter:
$$ d = 2r = 2 \times 3 = 6 \text{ units} $$
- Add the Curved Edge and the Diameter:
$$ P = \pi r + 2r = 3\pi + 6 \approx 9.42 + 6 = 15.42 \text{ units} $$
Example 2: Radius of 5 Units
- Identify the Radius:
Let the radius \( r \) be 5 units.
- Calculate the Circumference of the Full Circle:
$$ C = 2\pi r = 2\pi \times 5 = 10\pi \approx 31.42 \text{ units} $$
- Determine the Length of the Curved Edge:
$$ L = \pi r = \pi \times 5 = 5\pi \approx 15.71 \text{ units} $$
- Measure the Diameter:
$$ d = 2r = 2 \times 5 = 10 \text{ units} $$
- Add the Curved Edge and the Diameter:
$$ P = \pi r + 2r = 5\pi + 10 \approx 15.71 + 10 = 25.71 \text{ units} $$
Example 3: Radius of 8 Units
- Identify the Radius:
Let the radius \( r \) be 8 units.
- Calculate the Circumference of the Full Circle:
$$ C = 2\pi r = 2\pi \times 8 = 16\pi \approx 50.27 \text{ units} $$
- Determine the Length of the Curved Edge:
$$ L = \pi r = \pi \times 8 = 8\pi \approx 25.13 \text{ units} $$
- Measure the Diameter:
$$ d = 2r = 2 \times 8 = 16 \text{ units} $$
- Add the Curved Edge and the Diameter:
$$ P = \pi r + 2r = 8\pi + 16 \approx 25.13 + 16 = 41.13 \text{ units} $$
These examples demonstrate how to apply the formula to calculate the perimeter of a semi-circle for different radii. By following these steps, you can easily determine the perimeter for any semi-circle, which is useful for various mathematical and practical applications.
Examples of Perimeter Calculation
To understand the application of the perimeter formula for a semi-circle, let's go through a few detailed examples. These examples will help reinforce the concept and provide clarity on the steps involved in the calculation.
Example 1: Radius of 3 Units
- Identify the Radius:
Let the radius \( r \) be 3 units.
- Calculate the Circumference of the Full Circle:
$$ C = 2\pi r = 2\pi \times 3 = 6\pi \approx 18.85 \text{ units} $$
- Determine the Length of the Curved Edge:
$$ L = \pi r = \pi \times 3 = 3\pi \approx 9.42 \text{ units} $$
- Measure the Diameter:
$$ d = 2r = 2 \times 3 = 6 \text{ units} $$
- Add the Curved Edge and the Diameter:
$$ P = \pi r + 2r = 3\pi + 6 \approx 9.42 + 6 = 15.42 \text{ units} $$
Example 2: Radius of 5 Units
- Identify the Radius:
Let the radius \( r \) be 5 units.
- Calculate the Circumference of the Full Circle:
$$ C = 2\pi r = 2\pi \times 5 = 10\pi \approx 31.42 \text{ units} $$
- Determine the Length of the Curved Edge:
$$ L = \pi r = \pi \times 5 = 5\pi \approx 15.71 \text{ units} $$
- Measure the Diameter:
$$ d = 2r = 2 \times 5 = 10 \text{ units} $$
- Add the Curved Edge and the Diameter:
$$ P = \pi r + 2r = 5\pi + 10 \approx 15.71 + 10 = 25.71 \text{ units} $$
Example 3: Radius of 8 Units
- Identify the Radius:
Let the radius \( r \) be 8 units.
- Calculate the Circumference of the Full Circle:
$$ C = 2\pi r = 2\pi \times 8 = 16\pi \approx 50.27 \text{ units} $$
- Determine the Length of the Curved Edge:
$$ L = \pi r = \pi \times 8 = 8\pi \approx 25.13 \text{ units} $$
- Measure the Diameter:
$$ d = 2r = 2 \times 8 = 16 \text{ units} $$
- Add the Curved Edge and the Diameter:
$$ P = \pi r + 2r = 8\pi + 16 \approx 25.13 + 16 = 41.13 \text{ units} $$
These examples demonstrate how to apply the formula to calculate the perimeter of a semi-circle for different radii. By following these steps, you can easily determine the perimeter for any semi-circle, which is useful for various mathematical and practical applications.
Practical Applications of Semi-Circle Perimeter
The calculation of the perimeter of a semi-circle has numerous practical applications in various fields. Understanding how to determine this measurement can be beneficial for architects, engineers, designers, and many other professionals. Here are some key applications:
Architecture and Construction
- Designing Arches and Domes:
Architects often use semi-circles in the design of arches, domes, and other structures. Calculating the perimeter is essential for determining the materials needed and ensuring structural integrity.
- Curved Facades and Entryways:
Semi-circular designs are popular in creating aesthetically pleasing facades and entryways. Knowing the perimeter helps in planning the layout and construction details.
Landscaping and Garden Design
- Pathways and Edging:
Garden designers use semi-circles to create elegant pathways and borders. Calculating the perimeter is crucial for material estimation and layout planning.
- Water Features:
Semi-circular ponds and fountains are common in landscape designs. Knowing the perimeter aids in the design and implementation of these features.
Engineering
- Bridge and Tunnel Design:
Engineers use semi-circular designs for tunnels and bridges to optimize strength and durability. Calculating the perimeter is vital for construction and material specifications.
- Mechanical Parts:
Semi-circular components are used in various mechanical parts and systems. Understanding the perimeter helps in precise manufacturing and assembly.
Everyday Objects
- Furniture Design:
Semi-circular tables, shelves, and other furniture pieces are popular for their unique aesthetics. Calculating the perimeter ensures accurate design and material usage.
- Decorative Elements:
Decorative items such as mirrors, rugs, and frames often feature semi-circular shapes. Knowing the perimeter assists in designing and producing these items.
Education
- Teaching Geometry:
Understanding the perimeter of a semi-circle is a fundamental concept in geometry education. It helps students grasp broader mathematical principles and their real-world applications.
- Practical Projects:
Students can apply the concept in various projects, such as designing small structures, creating art pieces, or planning simple constructions.
These examples illustrate the diverse applications of calculating the perimeter of a semi-circle. Mastery of this concept can lead to more efficient designs, better material estimates, and overall improved project outcomes in various fields.
Practical Applications of Semi-Circle Perimeter
The calculation of the perimeter of a semi-circle has numerous practical applications in various fields. Understanding how to determine this measurement can be beneficial for architects, engineers, designers, and many other professionals. Here are some key applications:
Architecture and Construction
- Designing Arches and Domes:
Architects often use semi-circles in the design of arches, domes, and other structures. Calculating the perimeter is essential for determining the materials needed and ensuring structural integrity.
- Curved Facades and Entryways:
Semi-circular designs are popular in creating aesthetically pleasing facades and entryways. Knowing the perimeter helps in planning the layout and construction details.
Landscaping and Garden Design
- Pathways and Edging:
Garden designers use semi-circles to create elegant pathways and borders. Calculating the perimeter is crucial for material estimation and layout planning.
- Water Features:
Semi-circular ponds and fountains are common in landscape designs. Knowing the perimeter aids in the design and implementation of these features.
Engineering
- Bridge and Tunnel Design:
Engineers use semi-circular designs for tunnels and bridges to optimize strength and durability. Calculating the perimeter is vital for construction and material specifications.
- Mechanical Parts:
Semi-circular components are used in various mechanical parts and systems. Understanding the perimeter helps in precise manufacturing and assembly.
Everyday Objects
- Furniture Design:
Semi-circular tables, shelves, and other furniture pieces are popular for their unique aesthetics. Calculating the perimeter ensures accurate design and material usage.
- Decorative Elements:
Decorative items such as mirrors, rugs, and frames often feature semi-circular shapes. Knowing the perimeter assists in designing and producing these items.
Education
- Teaching Geometry:
Understanding the perimeter of a semi-circle is a fundamental concept in geometry education. It helps students grasp broader mathematical principles and their real-world applications.
- Practical Projects:
Students can apply the concept in various projects, such as designing small structures, creating art pieces, or planning simple constructions.
These examples illustrate the diverse applications of calculating the perimeter of a semi-circle. Mastery of this concept can lead to more efficient designs, better material estimates, and overall improved project outcomes in various fields.
Common Mistakes and How to Avoid Them
Calculating the perimeter of a semi-circle can sometimes lead to errors. Here are some common mistakes and tips on how to avoid them:
-
Incorrect Formula Usage:
Many students use the wrong formula. Remember, the perimeter (P) of a semi-circle is given by:
\[ P = \pi r + 2r \]
where \( r \) is the radius of the semi-circle. Ensure you're using the correct formula.
-
Confusing Diameter and Radius:
One common mistake is confusing the diameter (d) with the radius (r). Recall that the radius is half of the diameter:
\[ r = \frac{d}{2} \]
Always double-check whether you need to use the radius or the diameter in your calculations.
-
Forgetting to Include the Straight Edge:
The perimeter of a semi-circle includes both the curved part and the straight edge (diameter). A common mistake is to only calculate the curved part, which is:
\[ \text{Curved part} = \pi r \]
Always add the straight edge (2r) to get the correct perimeter.
-
Rounding Errors:
Rounding intermediate values can lead to inaccuracies. To avoid this, carry out calculations with full precision and round off only the final result.
-
Incorrect Use of Pi:
Ensure you use an accurate value for π (pi). For most calculations, using 3.14159 is sufficient, but for more precision, you can use more decimal places or a π function in your calculator.
By being aware of these common mistakes and following these tips, you can ensure accurate calculations of the semi-circle perimeter every time.

Common Mistakes and How to Avoid Them
Calculating the perimeter of a semi-circle can sometimes lead to errors. Here are some common mistakes and tips on how to avoid them:
-
Incorrect Formula Usage:
Many students use the wrong formula. Remember, the perimeter (P) of a semi-circle is given by:
\[ P = \pi r + 2r \]
where \( r \) is the radius of the semi-circle. Ensure you're using the correct formula.
-
Confusing Diameter and Radius:
One common mistake is confusing the diameter (d) with the radius (r). Recall that the radius is half of the diameter:
\[ r = \frac{d}{2} \]
Always double-check whether you need to use the radius or the diameter in your calculations.
-
Forgetting to Include the Straight Edge:
The perimeter of a semi-circle includes both the curved part and the straight edge (diameter). A common mistake is to only calculate the curved part, which is:
\[ \text{Curved part} = \pi r \]
Always add the straight edge (2r) to get the correct perimeter.
-
Rounding Errors:
Rounding intermediate values can lead to inaccuracies. To avoid this, carry out calculations with full precision and round off only the final result.
-
Incorrect Use of Pi:
Ensure you use an accurate value for π (pi). For most calculations, using 3.14159 is sufficient, but for more precision, you can use more decimal places or a π function in your calculator.
By being aware of these common mistakes and following these tips, you can ensure accurate calculations of the semi-circle perimeter every time.

Advanced Topics: Semi-Circle in Different Coordinate Systems
Understanding the geometry of a semi-circle in various coordinate systems can provide deeper insights into its properties and applications. Here, we will explore the semi-circle in Cartesian, polar, and cylindrical coordinate systems.
1. Cartesian Coordinate System
In the Cartesian coordinate system, the semi-circle is typically defined with its center at the origin (0, 0) and its radius r.
- The equation of a full circle is \(x^2 + y^2 = r^2\).
- For a semi-circle (considering the upper half), the equation is \(y = \sqrt{r^2 - x^2}\) for \( -r \leq x \leq r\).
Here, the perimeter includes the straight line segment along the diameter and the curved arc.
2. Polar Coordinate System
In the polar coordinate system, a point is represented as \((r, \theta)\), where r is the radial distance and \(\theta\) is the angular coordinate.
- The equation of a circle in polar coordinates is \(r = R\), where \(R\) is the radius.
- For a semi-circle, \(\theta\) ranges from \(0\) to \(\pi\) (for the upper half) or from \(-\pi\) to \(0\) (for the lower half).
The perimeter calculation in polar coordinates must account for the arc length and the straight-line segment along the diameter.
3. Cylindrical Coordinate System
The cylindrical coordinate system extends the polar coordinate system into three dimensions by adding a height (z) component.
- Coordinates are given as \((r, \theta, z)\).
- For a semi-circle lying in the xy-plane, the equations are \(r = R\) and \(0 \leq \theta \leq \pi\) (upper half) or \(-\pi \leq \theta \leq 0\) (lower half), with \(z = 0\).
This system is particularly useful when dealing with semi-circular shapes in three-dimensional space, such as a semi-cylindrical object.
Visualization and Transformations
Transforming between coordinate systems can provide different perspectives and simplify certain calculations:
- Cartesian to Polar: Use the transformations \(r = \sqrt{x^2 + y^2}\) and \(\theta = \arctan\left(\frac{y}{x}\right)\).
- Polar to Cartesian: Use the transformations \(x = r \cos(\theta)\) and \(y = r \sin(\theta)\).
- Cartesian to Cylindrical: Similar to Cartesian to Polar with the addition of \(z\): \(r = \sqrt{x^2 + y^2}\), \(\theta = \arctan\left(\frac{y}{x}\right)\), and \(z = z\).
- Cylindrical to Cartesian: Use \(x = r \cos(\theta)\), \(y = r \sin(\theta)\), and \(z = z\).
Applications
Understanding semi-circles in different coordinate systems is essential in fields like physics, engineering, and computer graphics. For instance, in physics, these concepts help in solving problems involving circular motion and fields, while in engineering, they are crucial for designing semi-circular structures and components.
By mastering these advanced topics, you can leverage different coordinate systems to tackle complex problems more effectively.
Advanced Topics: Semi-Circle in Different Coordinate Systems
Understanding the geometry of a semi-circle in various coordinate systems can provide deeper insights into its properties and applications. Here, we will explore the semi-circle in Cartesian, polar, and cylindrical coordinate systems.
1. Cartesian Coordinate System
In the Cartesian coordinate system, the semi-circle is typically defined with its center at the origin (0, 0) and its radius r.
- The equation of a full circle is \(x^2 + y^2 = r^2\).
- For a semi-circle (considering the upper half), the equation is \(y = \sqrt{r^2 - x^2}\) for \( -r \leq x \leq r\).
Here, the perimeter includes the straight line segment along the diameter and the curved arc.
2. Polar Coordinate System
In the polar coordinate system, a point is represented as \((r, \theta)\), where r is the radial distance and \(\theta\) is the angular coordinate.
- The equation of a circle in polar coordinates is \(r = R\), where \(R\) is the radius.
- For a semi-circle, \(\theta\) ranges from \(0\) to \(\pi\) (for the upper half) or from \(-\pi\) to \(0\) (for the lower half).
The perimeter calculation in polar coordinates must account for the arc length and the straight-line segment along the diameter.
3. Cylindrical Coordinate System
The cylindrical coordinate system extends the polar coordinate system into three dimensions by adding a height (z) component.
- Coordinates are given as \((r, \theta, z)\).
- For a semi-circle lying in the xy-plane, the equations are \(r = R\) and \(0 \leq \theta \leq \pi\) (upper half) or \(-\pi \leq \theta \leq 0\) (lower half), with \(z = 0\).
This system is particularly useful when dealing with semi-circular shapes in three-dimensional space, such as a semi-cylindrical object.
Visualization and Transformations
Transforming between coordinate systems can provide different perspectives and simplify certain calculations:
- Cartesian to Polar: Use the transformations \(r = \sqrt{x^2 + y^2}\) and \(\theta = \arctan\left(\frac{y}{x}\right)\).
- Polar to Cartesian: Use the transformations \(x = r \cos(\theta)\) and \(y = r \sin(\theta)\).
- Cartesian to Cylindrical: Similar to Cartesian to Polar with the addition of \(z\): \(r = \sqrt{x^2 + y^2}\), \(\theta = \arctan\left(\frac{y}{x}\right)\), and \(z = z\).
- Cylindrical to Cartesian: Use \(x = r \cos(\theta)\), \(y = r \sin(\theta)\), and \(z = z\).
Applications
Understanding semi-circles in different coordinate systems is essential in fields like physics, engineering, and computer graphics. For instance, in physics, these concepts help in solving problems involving circular motion and fields, while in engineering, they are crucial for designing semi-circular structures and components.
By mastering these advanced topics, you can leverage different coordinate systems to tackle complex problems more effectively.
Summary and Key Takeaways
The perimeter of a semi-circle is a fundamental concept in geometry, combining both the linear and curved aspects of a circle. Here are the key points to remember:
- The perimeter (or circumference) of a semi-circle includes half the circumference of the full circle plus the diameter.
- The formula for the perimeter of a semi-circle is given by: \[ P = \pi r + 2r \] where \( r \) is the radius of the circle.
- This can also be factored as: \[ P = r(\pi + 2) \]
- It is important to note that the perimeter of a semi-circle is not simply half the perimeter of the full circle due to the inclusion of the diameter.
- For a given diameter \( d \), the radius is \( r = \frac{d}{2} \) and the perimeter can be recalculated accordingly.
- When solving practical problems, ensure correct unit conversion and consistency, particularly when calculating using \( \pi \approx 3.14 \) or \( \frac{22}{7} \).
Examples:
- For a semi-circle with radius \( r = 5 \):
Perimeter:
\[ P = 5(\pi + 2) = 5(3.14 + 2) = 5 \times 5.14 = 25.7 \text{ units} \] - For a semi-circle with diameter \( d = 10 \):
Radius:
\[ r = \frac{10}{2} = 5 \]Perimeter:
\[ P = 5(\pi + 2) = 25.7 \text{ units} \]
These principles can be applied to various problems involving semi-circular shapes in different contexts, from simple geometry to complex engineering designs.
Remember, accuracy in calculation and understanding the geometric properties are crucial for effectively determining the perimeter of a semi-circle.
Summary and Key Takeaways
The perimeter of a semi-circle is a fundamental concept in geometry, combining both the linear and curved aspects of a circle. Here are the key points to remember:
- The perimeter (or circumference) of a semi-circle includes half the circumference of the full circle plus the diameter.
- The formula for the perimeter of a semi-circle is given by: \[ P = \pi r + 2r \] where \( r \) is the radius of the circle.
- This can also be factored as: \[ P = r(\pi + 2) \]
- It is important to note that the perimeter of a semi-circle is not simply half the perimeter of the full circle due to the inclusion of the diameter.
- For a given diameter \( d \), the radius is \( r = \frac{d}{2} \) and the perimeter can be recalculated accordingly.
- When solving practical problems, ensure correct unit conversion and consistency, particularly when calculating using \( \pi \approx 3.14 \) or \( \frac{22}{7} \).
Examples:
- For a semi-circle with radius \( r = 5 \):
Perimeter:
\[ P = 5(\pi + 2) = 5(3.14 + 2) = 5 \times 5.14 = 25.7 \text{ units} \] - For a semi-circle with diameter \( d = 10 \):
Radius:
\[ r = \frac{10}{2} = 5 \]Perimeter:
\[ P = 5(\pi + 2) = 25.7 \text{ units} \]
These principles can be applied to various problems involving semi-circular shapes in different contexts, from simple geometry to complex engineering designs.
Remember, accuracy in calculation and understanding the geometric properties are crucial for effectively determining the perimeter of a semi-circle.
Frequently Asked Questions (FAQs)
- What is the formula for the perimeter of a semi-circle?
- How do you derive the formula for the perimeter of a semi-circle?
- What is the difference between the perimeter and the circumference of a semi-circle?
- How can I calculate the perimeter of a semi-circle if I know the diameter?
- Can you provide an example of calculating the perimeter of a semi-circle?
- Use the formula: \( P = r(\pi + 2) \)
- Substitute the radius: \( P = 5(\pi + 2) \)
- Approximate \( \pi \) as 3.14: \( P = 5(3.14 + 2) \)
- Calculate: \( P = 5 \times 5.14 = 25.7 \) units
- Are there common mistakes to avoid when calculating the perimeter of a semi-circle?
- Only calculating the curved part and forgetting to add the diameter.
- Using an incorrect value for \( \pi \).
- Misidentifying the radius and diameter.
The formula for the perimeter of a semi-circle is given by \( P = r(\pi + 2) \), where \( r \) is the radius of the semi-circle and \( \pi \) is approximately 3.14.
The perimeter of a semi-circle includes the curved part and the straight diameter. The curved part is half the circumference of a full circle, which is \( \pi r \). Adding the diameter \( 2r \) to this, the formula becomes \( P = r(\pi + 2) \).
The circumference refers to the length of the curved part only, which is \( \pi r \). The perimeter includes both the curved part and the straight diameter, so it is \( r(\pi + 2) \).
If you know the diameter \( d \), first find the radius \( r \) by dividing the diameter by 2. Then use the formula \( P = r(\pi + 2) \).
Sure! For a semi-circle with a radius of 5 units:
Yes, common mistakes include:
Frequently Asked Questions (FAQs)
- What is the formula for the perimeter of a semi-circle?
- How do you derive the formula for the perimeter of a semi-circle?
- What is the difference between the perimeter and the circumference of a semi-circle?
- How can I calculate the perimeter of a semi-circle if I know the diameter?
- Can you provide an example of calculating the perimeter of a semi-circle?
- Use the formula: \( P = r(\pi + 2) \)
- Substitute the radius: \( P = 5(\pi + 2) \)
- Approximate \( \pi \) as 3.14: \( P = 5(3.14 + 2) \)
- Calculate: \( P = 5 \times 5.14 = 25.7 \) units
- Are there common mistakes to avoid when calculating the perimeter of a semi-circle?
- Only calculating the curved part and forgetting to add the diameter.
- Using an incorrect value for \( \pi \).
- Misidentifying the radius and diameter.
The formula for the perimeter of a semi-circle is given by \( P = r(\pi + 2) \), where \( r \) is the radius of the semi-circle and \( \pi \) is approximately 3.14.
The perimeter of a semi-circle includes the curved part and the straight diameter. The curved part is half the circumference of a full circle, which is \( \pi r \). Adding the diameter \( 2r \) to this, the formula becomes \( P = r(\pi + 2) \).
The circumference refers to the length of the curved part only, which is \( \pi r \). The perimeter includes both the curved part and the straight diameter, so it is \( r(\pi + 2) \).
If you know the diameter \( d \), first find the radius \( r \) by dividing the diameter by 2. Then use the formula \( P = r(\pi + 2) \).
Sure! For a semi-circle with a radius of 5 units:
Yes, common mistakes include:
Further Reading and Resources
To deepen your understanding of the semi-circle perimeter and related geometric concepts, here are some valuable resources and materials:
-
Textbooks and Articles
-
Geometry: A Comprehensive Course - This textbook provides detailed explanations of geometric shapes, including semi-circles, and their properties. It covers various geometric principles and their applications in real-world scenarios.
-
Online Article: - This article offers a thorough explanation of semi-circle properties, formulas for area and perimeter, and practical examples.
-
Online Article: - Detailed discussion on the semi-circle's definition, area, perimeter formulas, and solved examples to aid in understanding.
-
-
Interactive Tools and Calculators
-
- An interactive platform where you can visualize and manipulate semi-circles to understand their geometric properties better.
-
- This online calculator allows you to compute the area, perimeter, and other properties of a semi-circle by simply entering the radius or diameter.
-
-
Video Tutorials
-
- A series of video lessons explaining the concepts of area and perimeter of semi-circles, with step-by-step instructions and visual aids.
-
-
Practice Problems and Worksheets
-
- Printable worksheets for students to practice calculating the area and perimeter of semi-circles with varying levels of difficulty.
-
- Interactive and printable worksheets to help reinforce the concepts of semi-circle area and perimeter calculations.
-
These resources should provide a comprehensive understanding of the semi-circle perimeter and its applications. For further exploration, consider delving into advanced geometric texts or online courses that cover more complex geometric shapes and their properties.

Further Reading and Resources
To deepen your understanding of the semi-circle perimeter and related geometric concepts, here are some valuable resources and materials:
-
Textbooks and Articles
-
Geometry: A Comprehensive Course - This textbook provides detailed explanations of geometric shapes, including semi-circles, and their properties. It covers various geometric principles and their applications in real-world scenarios.
-
Online Article: - This article offers a thorough explanation of semi-circle properties, formulas for area and perimeter, and practical examples.
-
Online Article: - Detailed discussion on the semi-circle's definition, area, perimeter formulas, and solved examples to aid in understanding.
-
-
Interactive Tools and Calculators
-
- An interactive platform where you can visualize and manipulate semi-circles to understand their geometric properties better.
-
- This online calculator allows you to compute the area, perimeter, and other properties of a semi-circle by simply entering the radius or diameter.
-
-
Video Tutorials
-
- A series of video lessons explaining the concepts of area and perimeter of semi-circles, with step-by-step instructions and visual aids.
-
-
Practice Problems and Worksheets
-
- Printable worksheets for students to practice calculating the area and perimeter of semi-circles with varying levels of difficulty.
-
- Interactive and printable worksheets to help reinforce the concepts of semi-circle area and perimeter calculations.
-
These resources should provide a comprehensive understanding of the semi-circle perimeter and its applications. For further exploration, consider delving into advanced geometric texts or online courses that cover more complex geometric shapes and their properties.

Hướng dẫn chi tiết cách tính chu vi nửa hình tròn, giải thích công thức và ví dụ minh họa.
Cách Tính Chu Vi Nửa Hình Tròn
READ MORE:
Video hướng dẫn tính chu vi của nửa hình tròn từ Corbettmaths, phù hợp cho học sinh và những người yêu thích toán học.
Chu Vi Của Nửa Hình Tròn - Corbettmaths