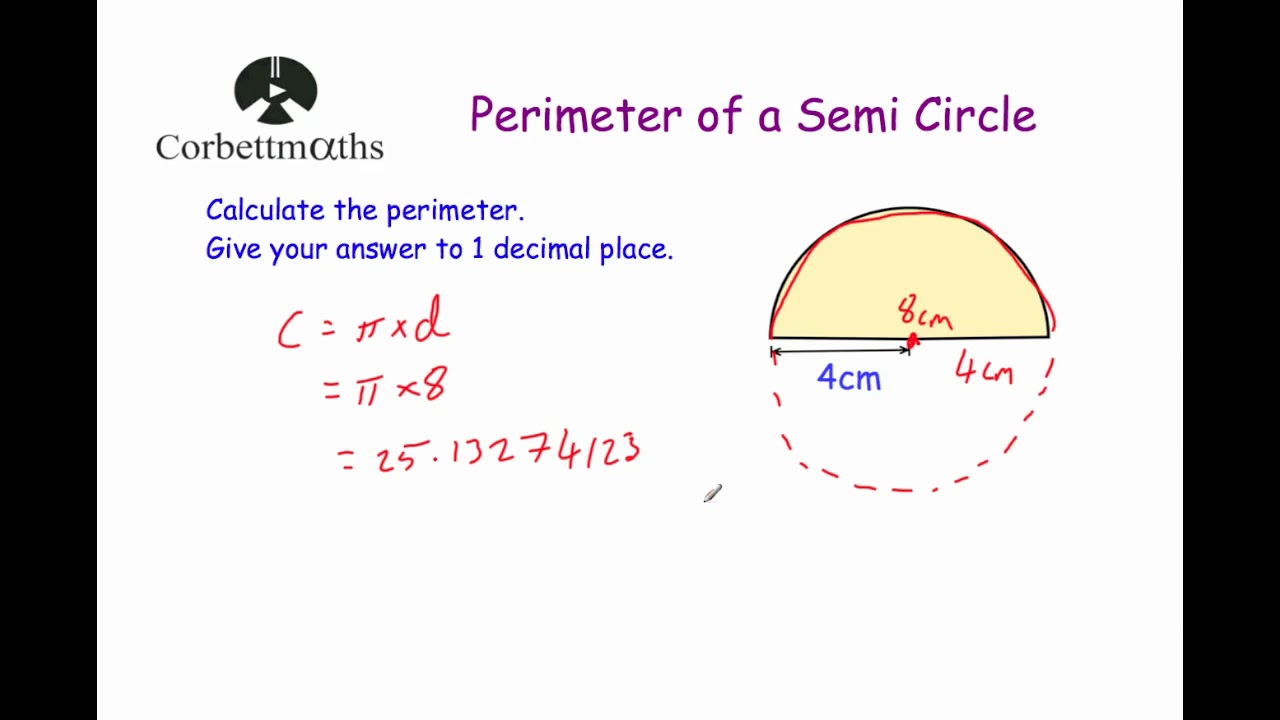
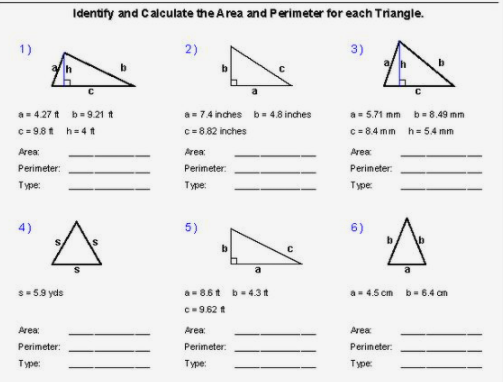
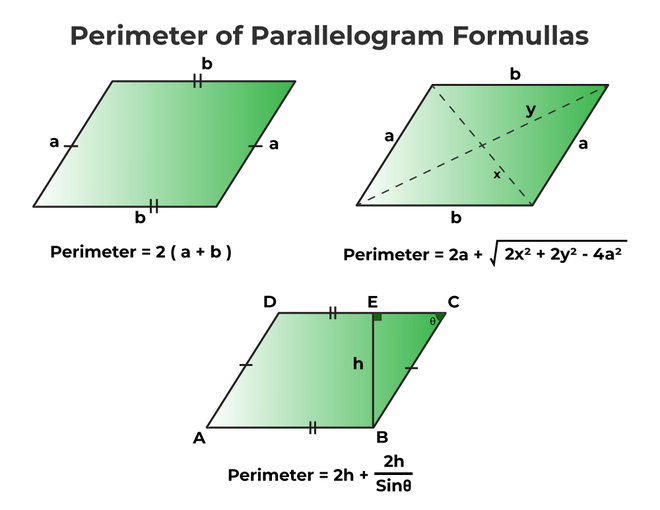
Topic perimeter of the polygon formula: Understanding the perimeter of the polygon formula is crucial for students and professionals in geometry. This guide will explore various methods to calculate the perimeter of different types of polygons, including regular and irregular shapes, and provide practical examples to enhance your comprehension. Dive in to master the essential concepts of polygon perimeters.
Table of Content
- Perimeter of a Polygon Formula
- Perimeter of a Polygon Formula
- Perimeter of a Polygon Formula
- Introduction to Polygon Perimeters
- Introduction to Polygon Perimeters
- Introduction to Polygon Perimeters
- Basic Definitions and Concepts
- Basic Definitions and Concepts
- Basic Definitions and Concepts
- Formulas for Regular Polygons
- Formulas for Regular Polygons
- Formulas for Regular Polygons
- Calculating Perimeters of Irregular Polygons
- Calculating Perimeters of Irregular Polygons
- Calculating Perimeters of Irregular Polygons
- Coordinate Geometry Approach
- Coordinate Geometry Approach
- Coordinate Geometry Approach
- Special Cases of Polygons
- Special Cases of Polygons
- Special Cases of Polygons
- Examples and Step-by-Step Solutions
- Examples and Step-by-Step Solutions
- Examples and Step-by-Step Solutions
- Applications in Real Life
- Applications in Real Life
- Applications in Real Life
- Common Mistakes and How to Avoid Them
- Common Mistakes and How to Avoid Them
- Common Mistakes and How to Avoid Them
- Advanced Topics and Further Reading
- Advanced Topics and Further Reading
- Advanced Topics and Further Reading
- YOUTUBE: Video hướng dẫn cách tính chu vi của các loại đa giác, giúp bạn nắm vững kiến thức toán học cơ bản.
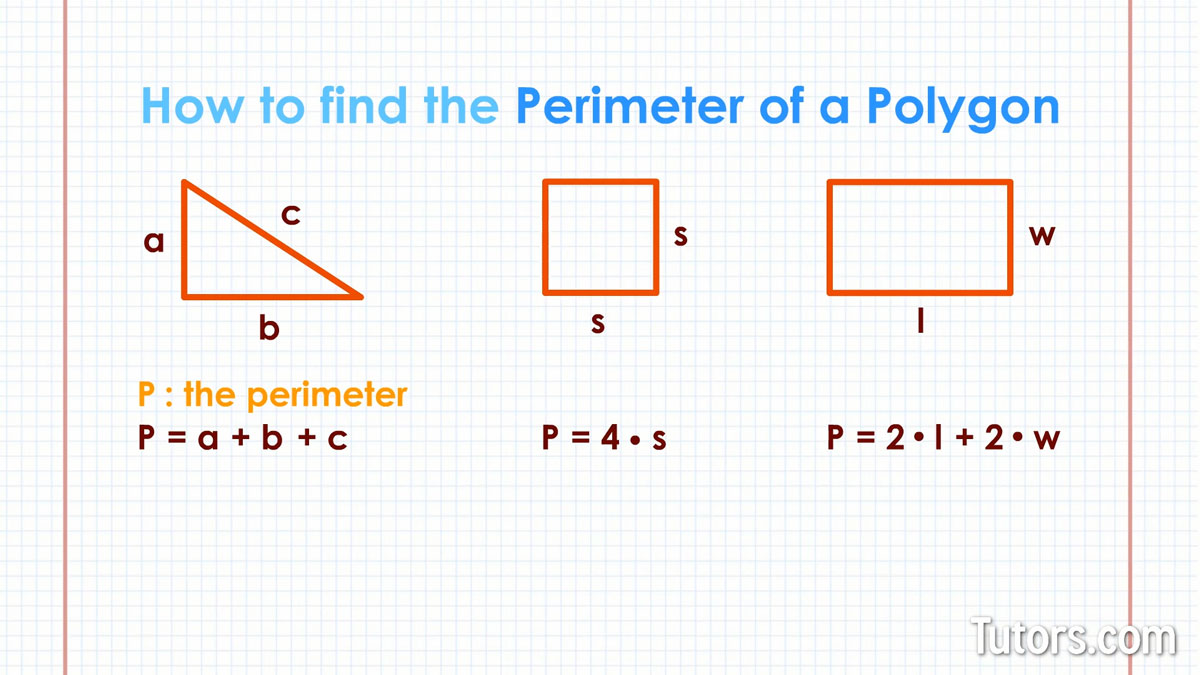
Perimeter of a Polygon Formula
The perimeter of a polygon is the total length of all its sides. Calculating the perimeter depends on the type of polygon and the available information. Below are various methods to find the perimeter of different polygons:
1. Regular Polygon
A regular polygon has all sides of equal length.
The formula for the perimeter \( P \) of a regular polygon with \( n \) sides, each of length \( a \), is given by:
2. Irregular Polygon
An irregular polygon has sides of different lengths.
The perimeter \( P \) is the sum of the lengths of all sides:
where \( a_1, a_2, \ldots, a_n \) are the lengths of the sides.
3. Polygon on a Coordinate Plane
If the vertices of the polygon are given in a coordinate plane, the perimeter can be calculated using the distance formula for each pair of consecutive vertices \((x_i, y_i)\) and \((x_{i+1}, y_{i+1})\).
The distance between two points \((x_i, y_i)\) and \((x_{i+1}, y_{i+1})\) is:
The perimeter \( P \) is then:
4. Special Polygons
- Rectangle: For a rectangle with length \( l \) and width \( w \), the perimeter is:
\[ P = 2l + 2w \] - Square: For a square with side length \( s \), the perimeter is:
\[ P = 4s \] - Triangle: For a triangle with sides \( a \), \( b \), and \( c \), the perimeter is:
\[ P = a + b + c \]

READ MORE:
Perimeter of a Polygon Formula
The perimeter of a polygon is the total length of all its sides. Calculating the perimeter depends on the type of polygon and the available information. Below are various methods to find the perimeter of different polygons:
1. Regular Polygon
A regular polygon has all sides of equal length.
The formula for the perimeter \( P \) of a regular polygon with \( n \) sides, each of length \( a \), is given by:
2. Irregular Polygon
An irregular polygon has sides of different lengths.
The perimeter \( P \) is the sum of the lengths of all sides:
where \( a_1, a_2, \ldots, a_n \) are the lengths of the sides.
3. Polygon on a Coordinate Plane
If the vertices of the polygon are given in a coordinate plane, the perimeter can be calculated using the distance formula for each pair of consecutive vertices \((x_i, y_i)\) and \((x_{i+1}, y_{i+1})\).
The distance between two points \((x_i, y_i)\) and \((x_{i+1}, y_{i+1})\) is:
The perimeter \( P \) is then:
4. Special Polygons
- Rectangle: For a rectangle with length \( l \) and width \( w \), the perimeter is:
\[ P = 2l + 2w \] - Square: For a square with side length \( s \), the perimeter is:
\[ P = 4s \] - Triangle: For a triangle with sides \( a \), \( b \), and \( c \), the perimeter is:
\[ P = a + b + c \]

Perimeter of a Polygon Formula
The perimeter of a polygon is the total length of all its sides. Calculating the perimeter depends on the type of polygon and the available information. Below are various methods to find the perimeter of different polygons:
1. Regular Polygon
A regular polygon has all sides of equal length.
The formula for the perimeter \( P \) of a regular polygon with \( n \) sides, each of length \( a \), is given by:
2. Irregular Polygon
An irregular polygon has sides of different lengths.
The perimeter \( P \) is the sum of the lengths of all sides:
where \( a_1, a_2, \ldots, a_n \) are the lengths of the sides.
3. Polygon on a Coordinate Plane
If the vertices of the polygon are given in a coordinate plane, the perimeter can be calculated using the distance formula for each pair of consecutive vertices \((x_i, y_i)\) and \((x_{i+1}, y_{i+1})\).
The distance between two points \((x_i, y_i)\) and \((x_{i+1}, y_{i+1})\) is:
The perimeter \( P \) is then:
4. Special Polygons
- Rectangle: For a rectangle with length \( l \) and width \( w \), the perimeter is:
\[ P = 2l + 2w \] - Square: For a square with side length \( s \), the perimeter is:
\[ P = 4s \] - Triangle: For a triangle with sides \( a \), \( b \), and \( c \), the perimeter is:
\[ P = a + b + c \]

Introduction to Polygon Perimeters
A polygon is a closed figure with straight sides. The perimeter of a polygon is the total length of its boundaries. Calculating the perimeter is essential in various fields such as geometry, engineering, and architecture. Understanding the perimeter of different types of polygons, including regular and irregular polygons, is crucial for solving real-world problems.
Here, we introduce the basic concepts and steps to calculate the perimeter of polygons:
- Regular Polygons: All sides and angles are equal. The perimeter can be easily calculated using the formula:
where \( n \) is the number of sides and \( a \) is the length of each side.\[ P = n \times a \] - Irregular Polygons: Sides and angles are not equal. The perimeter is the sum of the lengths of all sides:
where \( a_1, a_2, \ldots, a_n \) are the lengths of the sides.\[ P = a_1 + a_2 + a_3 + \cdots + a_n \] - Polygons on a Coordinate Plane: The perimeter can be calculated using the distance formula between consecutive vertices:
The total perimeter is:\[ d = \sqrt{(x_{i+1} - x_i)^2 + (y_{i+1} - y_i)^2} \] \[ P = \sum_{i=1}^{n} \sqrt{(x_{i+1} - x_i)^2 + (y_{i+1} - y_i)^2} \]
Calculating the perimeter of special polygons such as rectangles, squares, and triangles involves specific formulas:
- Rectangle: For a rectangle with length \( l \) and width \( w \), the perimeter is:
\[ P = 2l + 2w \] - Square: For a square with side length \( s \), the perimeter is:
\[ P = 4s \] - Triangle: For a triangle with sides \( a \), \( b \), and \( c \), the perimeter is:
\[ P = a + b + c \]
Mastering these formulas and understanding their applications will help you efficiently solve problems involving polygon perimeters.
Introduction to Polygon Perimeters
A polygon is a closed figure with straight sides. The perimeter of a polygon is the total length of its boundaries. Calculating the perimeter is essential in various fields such as geometry, engineering, and architecture. Understanding the perimeter of different types of polygons, including regular and irregular polygons, is crucial for solving real-world problems.
Here, we introduce the basic concepts and steps to calculate the perimeter of polygons:
- Regular Polygons: All sides and angles are equal. The perimeter can be easily calculated using the formula:
where \( n \) is the number of sides and \( a \) is the length of each side.\[ P = n \times a \] - Irregular Polygons: Sides and angles are not equal. The perimeter is the sum of the lengths of all sides:
where \( a_1, a_2, \ldots, a_n \) are the lengths of the sides.\[ P = a_1 + a_2 + a_3 + \cdots + a_n \] - Polygons on a Coordinate Plane: The perimeter can be calculated using the distance formula between consecutive vertices:
The total perimeter is:\[ d = \sqrt{(x_{i+1} - x_i)^2 + (y_{i+1} - y_i)^2} \] \[ P = \sum_{i=1}^{n} \sqrt{(x_{i+1} - x_i)^2 + (y_{i+1} - y_i)^2} \]
Calculating the perimeter of special polygons such as rectangles, squares, and triangles involves specific formulas:
- Rectangle: For a rectangle with length \( l \) and width \( w \), the perimeter is:
\[ P = 2l + 2w \] - Square: For a square with side length \( s \), the perimeter is:
\[ P = 4s \] - Triangle: For a triangle with sides \( a \), \( b \), and \( c \), the perimeter is:
\[ P = a + b + c \]
Mastering these formulas and understanding their applications will help you efficiently solve problems involving polygon perimeters.
Introduction to Polygon Perimeters
A polygon is a closed figure with straight sides. The perimeter of a polygon is the total length of its boundaries. Calculating the perimeter is essential in various fields such as geometry, engineering, and architecture. Understanding the perimeter of different types of polygons, including regular and irregular polygons, is crucial for solving real-world problems.
Here, we introduce the basic concepts and steps to calculate the perimeter of polygons:
- Regular Polygons: All sides and angles are equal. The perimeter can be easily calculated using the formula:
where \( n \) is the number of sides and \( a \) is the length of each side.\[ P = n \times a \] - Irregular Polygons: Sides and angles are not equal. The perimeter is the sum of the lengths of all sides:
where \( a_1, a_2, \ldots, a_n \) are the lengths of the sides.\[ P = a_1 + a_2 + a_3 + \cdots + a_n \] - Polygons on a Coordinate Plane: The perimeter can be calculated using the distance formula between consecutive vertices:
The total perimeter is:\[ d = \sqrt{(x_{i+1} - x_i)^2 + (y_{i+1} - y_i)^2} \] \[ P = \sum_{i=1}^{n} \sqrt{(x_{i+1} - x_i)^2 + (y_{i+1} - y_i)^2} \]
Calculating the perimeter of special polygons such as rectangles, squares, and triangles involves specific formulas:
- Rectangle: For a rectangle with length \( l \) and width \( w \), the perimeter is:
\[ P = 2l + 2w \] - Square: For a square with side length \( s \), the perimeter is:
\[ P = 4s \] - Triangle: For a triangle with sides \( a \), \( b \), and \( c \), the perimeter is:
\[ P = a + b + c \]
Mastering these formulas and understanding their applications will help you efficiently solve problems involving polygon perimeters.
Basic Definitions and Concepts
Understanding the perimeter of polygons requires familiarity with some basic definitions and concepts in geometry. Here are the fundamental terms and ideas:
- Polygon: A polygon is a two-dimensional geometric figure with a finite number of straight sides that form a closed loop. Each point where two sides meet is called a vertex.
- Sides: The straight edges of a polygon. The number of sides determines the type of polygon (e.g., triangle, quadrilateral, pentagon).
- Vertices: The points where two sides of a polygon meet. A polygon with \( n \) sides has \( n \) vertices.
- Perimeter: The total length of all the sides of a polygon. It is a measure of the distance around the polygon.
- Regular Polygon: A polygon with all sides and angles equal. Examples include equilateral triangles and squares.
- Irregular Polygon: A polygon with sides and/or angles that are not all equal. Most polygons fall into this category.
To calculate the perimeter of a polygon, consider the following general approach:
- Identify the Type of Polygon:
- If the polygon is regular, use the formula specific to regular polygons.
- If the polygon is irregular, sum the lengths of all its sides.
- Measure or Obtain Side Lengths: Measure the length of each side if not already given. In coordinate geometry, calculate the length of each side using the distance formula.
\[ d = \sqrt{(x_{i+1} - x_i)^2 + (y_{i+1} - y_i)^2} \] - Apply the Appropriate Formula: Use the relevant formula based on the type of polygon.
- For a regular polygon:
where \( n \) is the number of sides and \( a \) is the length of each side.\[ P = n \times a \] - For an irregular polygon:
where \( a_1, a_2, \ldots, a_n \) are the lengths of the sides.\[ P = a_1 + a_2 + a_3 + \cdots + a_n \]
- For a regular polygon:
Let's explore some specific cases to illustrate these concepts:
- Rectangle: For a rectangle with length \( l \) and width \( w \), the perimeter is:
\[ P = 2l + 2w \] - Square: For a square with side length \( s \), the perimeter is:
\[ P = 4s \] - Triangle: For a triangle with sides \( a \), \( b \), and \( c \), the perimeter is:
\[ P = a + b + c \]
Understanding these basic definitions and concepts is essential for calculating the perimeter of any polygon, whether regular or irregular.
Basic Definitions and Concepts
Understanding the perimeter of polygons requires familiarity with some basic definitions and concepts in geometry. Here are the fundamental terms and ideas:
- Polygon: A polygon is a two-dimensional geometric figure with a finite number of straight sides that form a closed loop. Each point where two sides meet is called a vertex.
- Sides: The straight edges of a polygon. The number of sides determines the type of polygon (e.g., triangle, quadrilateral, pentagon).
- Vertices: The points where two sides of a polygon meet. A polygon with \( n \) sides has \( n \) vertices.
- Perimeter: The total length of all the sides of a polygon. It is a measure of the distance around the polygon.
- Regular Polygon: A polygon with all sides and angles equal. Examples include equilateral triangles and squares.
- Irregular Polygon: A polygon with sides and/or angles that are not all equal. Most polygons fall into this category.
To calculate the perimeter of a polygon, consider the following general approach:
- Identify the Type of Polygon:
- If the polygon is regular, use the formula specific to regular polygons.
- If the polygon is irregular, sum the lengths of all its sides.
- Measure or Obtain Side Lengths: Measure the length of each side if not already given. In coordinate geometry, calculate the length of each side using the distance formula.
\[ d = \sqrt{(x_{i+1} - x_i)^2 + (y_{i+1} - y_i)^2} \] - Apply the Appropriate Formula: Use the relevant formula based on the type of polygon.
- For a regular polygon:
where \( n \) is the number of sides and \( a \) is the length of each side.\[ P = n \times a \] - For an irregular polygon:
where \( a_1, a_2, \ldots, a_n \) are the lengths of the sides.\[ P = a_1 + a_2 + a_3 + \cdots + a_n \]
- For a regular polygon:
Let's explore some specific cases to illustrate these concepts:
- Rectangle: For a rectangle with length \( l \) and width \( w \), the perimeter is:
\[ P = 2l + 2w \] - Square: For a square with side length \( s \), the perimeter is:
\[ P = 4s \] - Triangle: For a triangle with sides \( a \), \( b \), and \( c \), the perimeter is:
\[ P = a + b + c \]
Understanding these basic definitions and concepts is essential for calculating the perimeter of any polygon, whether regular or irregular.
Basic Definitions and Concepts
Understanding the perimeter of polygons requires familiarity with some basic definitions and concepts in geometry. Here are the fundamental terms and ideas:
- Polygon: A polygon is a two-dimensional geometric figure with a finite number of straight sides that form a closed loop. Each point where two sides meet is called a vertex.
- Sides: The straight edges of a polygon. The number of sides determines the type of polygon (e.g., triangle, quadrilateral, pentagon).
- Vertices: The points where two sides of a polygon meet. A polygon with \( n \) sides has \( n \) vertices.
- Perimeter: The total length of all the sides of a polygon. It is a measure of the distance around the polygon.
- Regular Polygon: A polygon with all sides and angles equal. Examples include equilateral triangles and squares.
- Irregular Polygon: A polygon with sides and/or angles that are not all equal. Most polygons fall into this category.
To calculate the perimeter of a polygon, consider the following general approach:
- Identify the Type of Polygon:
- If the polygon is regular, use the formula specific to regular polygons.
- If the polygon is irregular, sum the lengths of all its sides.
- Measure or Obtain Side Lengths: Measure the length of each side if not already given. In coordinate geometry, calculate the length of each side using the distance formula.
\[ d = \sqrt{(x_{i+1} - x_i)^2 + (y_{i+1} - y_i)^2} \] - Apply the Appropriate Formula: Use the relevant formula based on the type of polygon.
- For a regular polygon:
where \( n \) is the number of sides and \( a \) is the length of each side.\[ P = n \times a \] - For an irregular polygon:
where \( a_1, a_2, \ldots, a_n \) are the lengths of the sides.\[ P = a_1 + a_2 + a_3 + \cdots + a_n \]
- For a regular polygon:
Let's explore some specific cases to illustrate these concepts:
- Rectangle: For a rectangle with length \( l \) and width \( w \), the perimeter is:
\[ P = 2l + 2w \] - Square: For a square with side length \( s \), the perimeter is:
\[ P = 4s \] - Triangle: For a triangle with sides \( a \), \( b \), and \( c \), the perimeter is:
\[ P = a + b + c \]
Understanding these basic definitions and concepts is essential for calculating the perimeter of any polygon, whether regular or irregular.
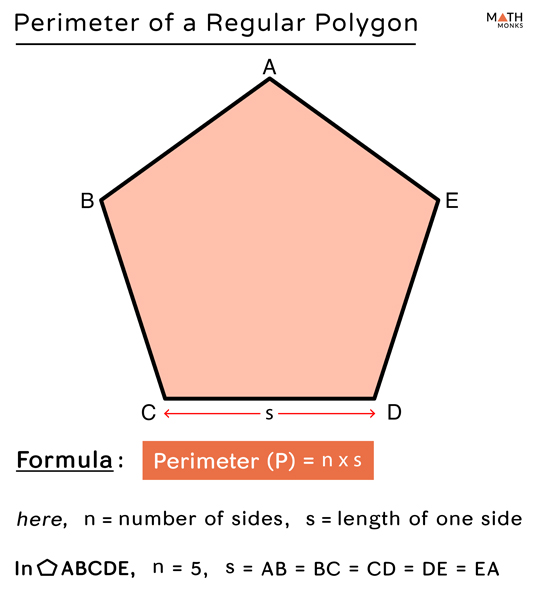
Formulas for Regular Polygons
A regular polygon is a polygon with all sides and all angles equal. Because of this uniformity, calculating the perimeter of a regular polygon is straightforward. Here are the steps and formulas used for common regular polygons:
- General Formula for Regular Polygons: For any regular polygon with \( n \) sides, each of length \( a \), the perimeter \( P \) is:
\[ P = n \times a \] - Equilateral Triangle: An equilateral triangle has three sides of equal length. If each side is \( a \), the perimeter \( P \) is:
\[ P = 3a \] - Square: A square has four sides of equal length. If each side is \( s \), the perimeter \( P \) is:
\[ P = 4s \] - Regular Pentagon: A regular pentagon has five sides of equal length. If each side is \( a \), the perimeter \( P \) is:
\[ P = 5a \] - Regular Hexagon: A regular hexagon has six sides of equal length. If each side is \( a \), the perimeter \( P \) is:
\[ P = 6a \] - Regular Octagon: A regular octagon has eight sides of equal length. If each side is \( a \), the perimeter \( P \) is:
\[ P = 8a \]
Let's summarize these formulas in a table for quick reference:
| Polygon | Number of Sides (\( n \)) | Perimeter Formula |
|---|---|---|
| Equilateral Triangle | 3 | |
| Square | 4 | |
| Regular Pentagon | 5 | |
| Regular Hexagon | 6 | |
| Regular Octagon | 8 |
Understanding these formulas makes it easier to calculate the perimeter of any regular polygon. With practice, you'll be able to quickly determine the perimeter by applying the appropriate formula for the given polygon.
Formulas for Regular Polygons
A regular polygon is a polygon with all sides and all angles equal. Because of this uniformity, calculating the perimeter of a regular polygon is straightforward. Here are the steps and formulas used for common regular polygons:
- General Formula for Regular Polygons: For any regular polygon with \( n \) sides, each of length \( a \), the perimeter \( P \) is:
\[ P = n \times a \] - Equilateral Triangle: An equilateral triangle has three sides of equal length. If each side is \( a \), the perimeter \( P \) is:
\[ P = 3a \] - Square: A square has four sides of equal length. If each side is \( s \), the perimeter \( P \) is:
\[ P = 4s \] - Regular Pentagon: A regular pentagon has five sides of equal length. If each side is \( a \), the perimeter \( P \) is:
\[ P = 5a \] - Regular Hexagon: A regular hexagon has six sides of equal length. If each side is \( a \), the perimeter \( P \) is:
\[ P = 6a \] - Regular Octagon: A regular octagon has eight sides of equal length. If each side is \( a \), the perimeter \( P \) is:
\[ P = 8a \]
Let's summarize these formulas in a table for quick reference:
| Polygon | Number of Sides (\( n \)) | Perimeter Formula |
|---|---|---|
| Equilateral Triangle | 3 | |
| Square | 4 | |
| Regular Pentagon | 5 | |
| Regular Hexagon | 6 | |
| Regular Octagon | 8 |
Understanding these formulas makes it easier to calculate the perimeter of any regular polygon. With practice, you'll be able to quickly determine the perimeter by applying the appropriate formula for the given polygon.
Formulas for Regular Polygons
A regular polygon is a polygon with all sides and all angles equal. Because of this uniformity, calculating the perimeter of a regular polygon is straightforward. Here are the steps and formulas used for common regular polygons:
- General Formula for Regular Polygons: For any regular polygon with \( n \) sides, each of length \( a \), the perimeter \( P \) is:
\[ P = n \times a \] - Equilateral Triangle: An equilateral triangle has three sides of equal length. If each side is \( a \), the perimeter \( P \) is:
\[ P = 3a \] - Square: A square has four sides of equal length. If each side is \( s \), the perimeter \( P \) is:
\[ P = 4s \] - Regular Pentagon: A regular pentagon has five sides of equal length. If each side is \( a \), the perimeter \( P \) is:
\[ P = 5a \] - Regular Hexagon: A regular hexagon has six sides of equal length. If each side is \( a \), the perimeter \( P \) is:
\[ P = 6a \] - Regular Octagon: A regular octagon has eight sides of equal length. If each side is \( a \), the perimeter \( P \) is:
\[ P = 8a \]
Let's summarize these formulas in a table for quick reference:
| Polygon | Number of Sides (\( n \)) | Perimeter Formula |
|---|---|---|
| Equilateral Triangle | 3 | |
| Square | 4 | |
| Regular Pentagon | 5 | |
| Regular Hexagon | 6 | |
| Regular Octagon | 8 |
Understanding these formulas makes it easier to calculate the perimeter of any regular polygon. With practice, you'll be able to quickly determine the perimeter by applying the appropriate formula for the given polygon.
Calculating Perimeters of Irregular Polygons
Unlike regular polygons, irregular polygons have sides of different lengths. Calculating the perimeter of an irregular polygon involves summing the lengths of all its sides. Here's a detailed step-by-step guide to help you through the process:
- Identify and Measure All Sides:
- List all sides of the polygon and measure their lengths. Each side should be measured accurately.
- Sum the Lengths of All Sides:
Add the lengths of all sides together to find the perimeter. The formula for the perimeter \( P \) is:
\[ P = a_1 + a_2 + a_3 + \cdots + a_n \] where \( a_1, a_2, \ldots, a_n \) are the lengths of the sides.
- Example Calculation:
- Consider an irregular polygon with side lengths of 3 cm, 4 cm, 5 cm, 6 cm, and 7 cm.
- The perimeter \( P \) is calculated as:
\[ P = 3 + 4 + 5 + 6 + 7 = 25 \text{ cm} \]
In cases where the coordinates of the vertices of the polygon are given, you can use the distance formula to calculate the length of each side. Here's how:
- Identify Coordinates of Vertices:
List the coordinates of each vertex in the order they connect.
- Apply the Distance Formula:
Use the distance formula to find the length of each side between consecutive vertices \((x_i, y_i)\) and \((x_{i+1}, y_{i+1})\):
\[ d = \sqrt{(x_{i+1} - x_i)^2 + (y_{i+1} - y_i)^2} \] - Sum the Lengths:
Add up all the side lengths calculated using the distance formula to get the perimeter.
- Example: For a polygon with vertices at (0,0), (3,0), (3,4), and (0,4):
The side lengths are:
\[ d_1 = \sqrt{(3-0)^2 + (0-0)^2} = 3 \] \[ d_2 = \sqrt{(3-3)^2 + (4-0)^2} = 4 \] \[ d_3 = \sqrt{(0-3)^2 + (4-4)^2} = 3 \] \[ d_4 = \sqrt{(0-0)^2 + (0-4)^2} = 4 \] The perimeter \( P \) is:
\[ P = 3 + 4 + 3 + 4 = 14 \text{ units} \]
- Example: For a polygon with vertices at (0,0), (3,0), (3,4), and (0,4):
By following these steps, you can accurately calculate the perimeter of any irregular polygon, whether the side lengths are given directly or you need to determine them using vertex coordinates.
Calculating Perimeters of Irregular Polygons
Unlike regular polygons, irregular polygons have sides of different lengths. Calculating the perimeter of an irregular polygon involves summing the lengths of all its sides. Here's a detailed step-by-step guide to help you through the process:
- Identify and Measure All Sides:
- List all sides of the polygon and measure their lengths. Each side should be measured accurately.
- Sum the Lengths of All Sides:
Add the lengths of all sides together to find the perimeter. The formula for the perimeter \( P \) is:
\[ P = a_1 + a_2 + a_3 + \cdots + a_n \] where \( a_1, a_2, \ldots, a_n \) are the lengths of the sides.
- Example Calculation:
- Consider an irregular polygon with side lengths of 3 cm, 4 cm, 5 cm, 6 cm, and 7 cm.
- The perimeter \( P \) is calculated as:
\[ P = 3 + 4 + 5 + 6 + 7 = 25 \text{ cm} \]
In cases where the coordinates of the vertices of the polygon are given, you can use the distance formula to calculate the length of each side. Here's how:
- Identify Coordinates of Vertices:
List the coordinates of each vertex in the order they connect.
- Apply the Distance Formula:
Use the distance formula to find the length of each side between consecutive vertices \((x_i, y_i)\) and \((x_{i+1}, y_{i+1})\):
\[ d = \sqrt{(x_{i+1} - x_i)^2 + (y_{i+1} - y_i)^2} \] - Sum the Lengths:
Add up all the side lengths calculated using the distance formula to get the perimeter.
- Example: For a polygon with vertices at (0,0), (3,0), (3,4), and (0,4):
The side lengths are:
\[ d_1 = \sqrt{(3-0)^2 + (0-0)^2} = 3 \] \[ d_2 = \sqrt{(3-3)^2 + (4-0)^2} = 4 \] \[ d_3 = \sqrt{(0-3)^2 + (4-4)^2} = 3 \] \[ d_4 = \sqrt{(0-0)^2 + (0-4)^2} = 4 \] The perimeter \( P \) is:
\[ P = 3 + 4 + 3 + 4 = 14 \text{ units} \]
- Example: For a polygon with vertices at (0,0), (3,0), (3,4), and (0,4):
By following these steps, you can accurately calculate the perimeter of any irregular polygon, whether the side lengths are given directly or you need to determine them using vertex coordinates.

Calculating Perimeters of Irregular Polygons
Unlike regular polygons, irregular polygons have sides of different lengths. Calculating the perimeter of an irregular polygon involves summing the lengths of all its sides. Here's a detailed step-by-step guide to help you through the process:
- Identify and Measure All Sides:
- List all sides of the polygon and measure their lengths. Each side should be measured accurately.
- Sum the Lengths of All Sides:
Add the lengths of all sides together to find the perimeter. The formula for the perimeter \( P \) is:
\[ P = a_1 + a_2 + a_3 + \cdots + a_n \] where \( a_1, a_2, \ldots, a_n \) are the lengths of the sides.
- Example Calculation:
- Consider an irregular polygon with side lengths of 3 cm, 4 cm, 5 cm, 6 cm, and 7 cm.
- The perimeter \( P \) is calculated as:
\[ P = 3 + 4 + 5 + 6 + 7 = 25 \text{ cm} \]
In cases where the coordinates of the vertices of the polygon are given, you can use the distance formula to calculate the length of each side. Here's how:
- Identify Coordinates of Vertices:
List the coordinates of each vertex in the order they connect.
- Apply the Distance Formula:
Use the distance formula to find the length of each side between consecutive vertices \((x_i, y_i)\) and \((x_{i+1}, y_{i+1})\):
\[ d = \sqrt{(x_{i+1} - x_i)^2 + (y_{i+1} - y_i)^2} \] - Sum the Lengths:
Add up all the side lengths calculated using the distance formula to get the perimeter.
- Example: For a polygon with vertices at (0,0), (3,0), (3,4), and (0,4):
The side lengths are:
\[ d_1 = \sqrt{(3-0)^2 + (0-0)^2} = 3 \] \[ d_2 = \sqrt{(3-3)^2 + (4-0)^2} = 4 \] \[ d_3 = \sqrt{(0-3)^2 + (4-4)^2} = 3 \] \[ d_4 = \sqrt{(0-0)^2 + (0-4)^2} = 4 \] The perimeter \( P \) is:
\[ P = 3 + 4 + 3 + 4 = 14 \text{ units} \]
- Example: For a polygon with vertices at (0,0), (3,0), (3,4), and (0,4):
By following these steps, you can accurately calculate the perimeter of any irregular polygon, whether the side lengths are given directly or you need to determine them using vertex coordinates.

Coordinate Geometry Approach
Calculating the perimeter of a polygon using coordinate geometry involves determining the distances between each pair of consecutive vertices of the polygon. This method is especially useful for polygons with vertices defined by coordinates on the Cartesian plane.
Let's break down the steps to calculate the perimeter of a polygon using the coordinate geometry approach:
- List the coordinates of the vertices: Ensure that the coordinates are in the correct order, either clockwise or counterclockwise, to accurately reflect the shape of the polygon.
- Apply the distance formula: The distance between two points \((x_1, y_1)\) and \((x_2, y_2)\) is given by:
\( d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \) - Calculate the distance for each pair of consecutive vertices: Use the distance formula for each segment of the polygon.
- Sum the distances: Add all the distances to get the perimeter of the polygon.
Here is an example to illustrate these steps:
- Consider a triangle with vertices at \(A(1, 2)\), \(B(4, 6)\), and \(C(7, 2)\).
- Calculate the distances between consecutive vertices:
- Distance between \(A\) and \(B\):
\( AB = \sqrt{(4 - 1)^2 + (6 - 2)^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \) - Distance between \(B\) and \(C\):
\( BC = \sqrt{(7 - 4)^2 + (2 - 6)^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \) - Distance between \(C\) and \(A\):
\( CA = \sqrt{(7 - 1)^2 + (2 - 2)^2} = \sqrt{36 + 0} = \sqrt{36} = 6 \) - Sum the distances to get the perimeter:
\( \text{Perimeter} = AB + BC + CA = 5 + 5 + 6 = 16 \)
Using this method, you can calculate the perimeter of any polygon provided the coordinates of its vertices are known. This approach is versatile and can be applied to both regular and irregular polygons.
Coordinate Geometry Approach
Calculating the perimeter of a polygon using coordinate geometry involves determining the distances between each pair of consecutive vertices of the polygon. This method is especially useful for polygons with vertices defined by coordinates on the Cartesian plane.
Let's break down the steps to calculate the perimeter of a polygon using the coordinate geometry approach:
- List the coordinates of the vertices: Ensure that the coordinates are in the correct order, either clockwise or counterclockwise, to accurately reflect the shape of the polygon.
- Apply the distance formula: The distance between two points \((x_1, y_1)\) and \((x_2, y_2)\) is given by:
\( d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \) - Calculate the distance for each pair of consecutive vertices: Use the distance formula for each segment of the polygon.
- Sum the distances: Add all the distances to get the perimeter of the polygon.
Here is an example to illustrate these steps:
- Consider a triangle with vertices at \(A(1, 2)\), \(B(4, 6)\), and \(C(7, 2)\).
- Calculate the distances between consecutive vertices:
- Distance between \(A\) and \(B\):
\( AB = \sqrt{(4 - 1)^2 + (6 - 2)^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \) - Distance between \(B\) and \(C\):
\( BC = \sqrt{(7 - 4)^2 + (2 - 6)^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \) - Distance between \(C\) and \(A\):
\( CA = \sqrt{(7 - 1)^2 + (2 - 2)^2} = \sqrt{36 + 0} = \sqrt{36} = 6 \) - Sum the distances to get the perimeter:
\( \text{Perimeter} = AB + BC + CA = 5 + 5 + 6 = 16 \)
Using this method, you can calculate the perimeter of any polygon provided the coordinates of its vertices are known. This approach is versatile and can be applied to both regular and irregular polygons.
Coordinate Geometry Approach
Calculating the perimeter of a polygon using coordinate geometry involves determining the distances between each pair of consecutive vertices of the polygon. This method is especially useful for polygons with vertices defined by coordinates on the Cartesian plane.
Let's break down the steps to calculate the perimeter of a polygon using the coordinate geometry approach:
- List the coordinates of the vertices: Ensure that the coordinates are in the correct order, either clockwise or counterclockwise, to accurately reflect the shape of the polygon.
- Apply the distance formula: The distance between two points \((x_1, y_1)\) and \((x_2, y_2)\) is given by:
\( d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \) - Calculate the distance for each pair of consecutive vertices: Use the distance formula for each segment of the polygon.
- Sum the distances: Add all the distances to get the perimeter of the polygon.
Here is an example to illustrate these steps:
- Consider a triangle with vertices at \(A(1, 2)\), \(B(4, 6)\), and \(C(7, 2)\).
- Calculate the distances between consecutive vertices:
- Distance between \(A\) and \(B\):
\( AB = \sqrt{(4 - 1)^2 + (6 - 2)^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \) - Distance between \(B\) and \(C\):
\( BC = \sqrt{(7 - 4)^2 + (2 - 6)^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \) - Distance between \(C\) and \(A\):
\( CA = \sqrt{(7 - 1)^2 + (2 - 2)^2} = \sqrt{36 + 0} = \sqrt{36} = 6 \) - Sum the distances to get the perimeter:
\( \text{Perimeter} = AB + BC + CA = 5 + 5 + 6 = 16 \)
Using this method, you can calculate the perimeter of any polygon provided the coordinates of its vertices are known. This approach is versatile and can be applied to both regular and irregular polygons.
Special Cases of Polygons
Polygons come in various special forms where unique properties and simplified formulas for calculating the perimeter can be applied. Let's explore some common special cases of polygons.
Square
A square is a regular polygon with four equal sides and four right angles.
- Formula: \( P = 4a \)
- Example: If the side length \( a = 5 \, \text{cm} \), then the perimeter \( P = 4 \times 5 = 20 \, \text{cm} \).
Rectangle
A rectangle is a quadrilateral with opposite sides equal and four right angles.
- Formula: \( P = 2(l + b) \)
- Example: If the length \( l = 8 \, \text{cm} \) and breadth \( b = 4 \, \text{cm} \), then the perimeter \( P = 2(8 + 4) = 24 \, \text{cm} \).
Equilateral Triangle
An equilateral triangle has all three sides of equal length.
- Formula: \( P = 3a \)
- Example: If the side length \( a = 6 \, \text{cm} \), then the perimeter \( P = 3 \times 6 = 18 \, \text{cm} \).
Regular Pentagon
A regular pentagon has five sides of equal length.
- Formula: \( P = 5a \)
- Example: If the side length \( a = 7 \, \text{cm} \), then the perimeter \( P = 5 \times 7 = 35 \, \text{cm} \).
Regular Hexagon
A regular hexagon has six sides of equal length.
- Formula: \( P = 6a \)
- Example: If the side length \( a = 10 \, \text{cm} \), then the perimeter \( P = 6 \times 10 = 60 \, \text{cm} \).
Rhombus
A rhombus is a quadrilateral with all sides of equal length but not necessarily right angles.
- Formula: \( P = 4a \)
- Example: If the side length \( a = 9 \, \text{cm} \), then the perimeter \( P = 4 \times 9 = 36 \, \text{cm} \).
Trapezoid
A trapezoid (or trapezium) is a quadrilateral with at least one pair of parallel sides.
- Formula: \( P = a + b + c + d \) (sum of all sides)
- Example: If the sides are \( a = 5 \, \text{cm} \), \( b = 6 \, \text{cm} \), \( c = 4 \, \text{cm} \), and \( d = 7 \, \text{cm} \), then the perimeter \( P = 5 + 6 + 4 + 7 = 22 \, \text{cm} \).
Parallelogram
A parallelogram is a quadrilateral with opposite sides equal and parallel.
- Formula: \( P = 2(l + b) \)
- Example: If the length \( l = 12 \, \text{cm} \) and breadth \( b = 5 \, \text{cm} \), then the perimeter \( P = 2(12 + 5) = 34 \, \text{cm} \).
Special Cases of Polygons
Polygons come in various special forms where unique properties and simplified formulas for calculating the perimeter can be applied. Let's explore some common special cases of polygons.
Square
A square is a regular polygon with four equal sides and four right angles.
- Formula: \( P = 4a \)
- Example: If the side length \( a = 5 \, \text{cm} \), then the perimeter \( P = 4 \times 5 = 20 \, \text{cm} \).
Rectangle
A rectangle is a quadrilateral with opposite sides equal and four right angles.
- Formula: \( P = 2(l + b) \)
- Example: If the length \( l = 8 \, \text{cm} \) and breadth \( b = 4 \, \text{cm} \), then the perimeter \( P = 2(8 + 4) = 24 \, \text{cm} \).
Equilateral Triangle
An equilateral triangle has all three sides of equal length.
- Formula: \( P = 3a \)
- Example: If the side length \( a = 6 \, \text{cm} \), then the perimeter \( P = 3 \times 6 = 18 \, \text{cm} \).
Regular Pentagon
A regular pentagon has five sides of equal length.
- Formula: \( P = 5a \)
- Example: If the side length \( a = 7 \, \text{cm} \), then the perimeter \( P = 5 \times 7 = 35 \, \text{cm} \).
Regular Hexagon
A regular hexagon has six sides of equal length.
- Formula: \( P = 6a \)
- Example: If the side length \( a = 10 \, \text{cm} \), then the perimeter \( P = 6 \times 10 = 60 \, \text{cm} \).
Rhombus
A rhombus is a quadrilateral with all sides of equal length but not necessarily right angles.
- Formula: \( P = 4a \)
- Example: If the side length \( a = 9 \, \text{cm} \), then the perimeter \( P = 4 \times 9 = 36 \, \text{cm} \).
Trapezoid
A trapezoid (or trapezium) is a quadrilateral with at least one pair of parallel sides.
- Formula: \( P = a + b + c + d \) (sum of all sides)
- Example: If the sides are \( a = 5 \, \text{cm} \), \( b = 6 \, \text{cm} \), \( c = 4 \, \text{cm} \), and \( d = 7 \, \text{cm} \), then the perimeter \( P = 5 + 6 + 4 + 7 = 22 \, \text{cm} \).
Parallelogram
A parallelogram is a quadrilateral with opposite sides equal and parallel.
- Formula: \( P = 2(l + b) \)
- Example: If the length \( l = 12 \, \text{cm} \) and breadth \( b = 5 \, \text{cm} \), then the perimeter \( P = 2(12 + 5) = 34 \, \text{cm} \).
Special Cases of Polygons
Polygons come in various special forms where unique properties and simplified formulas for calculating the perimeter can be applied. Let's explore some common special cases of polygons.
Square
A square is a regular polygon with four equal sides and four right angles.
- Formula: \( P = 4a \)
- Example: If the side length \( a = 5 \, \text{cm} \), then the perimeter \( P = 4 \times 5 = 20 \, \text{cm} \).
Rectangle
A rectangle is a quadrilateral with opposite sides equal and four right angles.
- Formula: \( P = 2(l + b) \)
- Example: If the length \( l = 8 \, \text{cm} \) and breadth \( b = 4 \, \text{cm} \), then the perimeter \( P = 2(8 + 4) = 24 \, \text{cm} \).
Equilateral Triangle
An equilateral triangle has all three sides of equal length.
- Formula: \( P = 3a \)
- Example: If the side length \( a = 6 \, \text{cm} \), then the perimeter \( P = 3 \times 6 = 18 \, \text{cm} \).
Regular Pentagon
A regular pentagon has five sides of equal length.
- Formula: \( P = 5a \)
- Example: If the side length \( a = 7 \, \text{cm} \), then the perimeter \( P = 5 \times 7 = 35 \, \text{cm} \).
Regular Hexagon
A regular hexagon has six sides of equal length.
- Formula: \( P = 6a \)
- Example: If the side length \( a = 10 \, \text{cm} \), then the perimeter \( P = 6 \times 10 = 60 \, \text{cm} \).
Rhombus
A rhombus is a quadrilateral with all sides of equal length but not necessarily right angles.
- Formula: \( P = 4a \)
- Example: If the side length \( a = 9 \, \text{cm} \), then the perimeter \( P = 4 \times 9 = 36 \, \text{cm} \).
Trapezoid
A trapezoid (or trapezium) is a quadrilateral with at least one pair of parallel sides.
- Formula: \( P = a + b + c + d \) (sum of all sides)
- Example: If the sides are \( a = 5 \, \text{cm} \), \( b = 6 \, \text{cm} \), \( c = 4 \, \text{cm} \), and \( d = 7 \, \text{cm} \), then the perimeter \( P = 5 + 6 + 4 + 7 = 22 \, \text{cm} \).
Parallelogram
A parallelogram is a quadrilateral with opposite sides equal and parallel.
- Formula: \( P = 2(l + b) \)
- Example: If the length \( l = 12 \, \text{cm} \) and breadth \( b = 5 \, \text{cm} \), then the perimeter \( P = 2(12 + 5) = 34 \, \text{cm} \).
Examples and Step-by-Step Solutions
In this section, we will explore a few examples that demonstrate how to calculate the perimeter of various polygons using step-by-step solutions. Understanding these examples will help reinforce the concepts and formulas discussed earlier.
Example 1: Perimeter of a Square
Given a square with a side length of \(4\) units, we can calculate its perimeter using the formula:
\[ \text{Perimeter} = 4 \times \text{side length} \]
Substituting the given side length:
\[ \text{Perimeter} = 4 \times 4 = 16 \text{ units} \]
Example 2: Perimeter of a Rectangle
Consider a rectangle with a length of \(7\) units and a width of \(3\) units. The formula to calculate the perimeter is:
\[ \text{Perimeter} = 2 \times (\text{length} + \text{width}) \]
Substituting the given dimensions:
\[ \text{Perimeter} = 2 \times (7 + 3) = 2 \times 10 = 20 \text{ units} \]
Example 3: Perimeter of an Irregular Polygon
For an irregular polygon with side lengths of \(5\) units, \(3\) units, \(7\) units, and \(4\) units, the perimeter is calculated by summing the lengths of all sides:
\[ \text{Perimeter} = 5 + 3 + 7 + 4 = 19 \text{ units} \]
Example 4: Perimeter of an Equilateral Triangle
Given an equilateral triangle with a perimeter of \(27\) units, we can find the length of one side. The formula for the perimeter of an equilateral triangle is:
\[ \text{Perimeter} = 3 \times \text{side length} \]
Rearranging the formula to solve for the side length:
\[ \text{side length} = \frac{\text{Perimeter}}{3} = \frac{27}{3} = 9 \text{ units} \]
Example 5: Finding a Missing Side Length
Consider a polygon with sides \(AB = 3\) units, \(BC = 4\) units, \(CD = 6\) units, \(DE = 2\) units, \(EF = 1.5\) units, and an unknown side \(FA\). Given that the perimeter of the polygon is \(18.5\) units, we can find the missing side \(FA\) by subtracting the sum of the known sides from the total perimeter:
\[ 18.5 = 3 + 4 + 6 + 2 + 1.5 + FA \]
\[ FA = 18.5 - (3 + 4 + 6 + 2 + 1.5) = 18.5 - 16.5 = 2 \text{ units} \]
Example 6: Perimeter of a Regular Pentagon
For a regular pentagon with a side length of \(5\) units, the perimeter is calculated as:
\[ \text{Perimeter} = 5 \times \text{side length} = 5 \times 5 = 25 \text{ units} \]
These examples illustrate how to apply the perimeter formulas to different types of polygons. By following these steps, you can confidently calculate the perimeter of any polygon you encounter.
Examples and Step-by-Step Solutions
In this section, we will explore a few examples that demonstrate how to calculate the perimeter of various polygons using step-by-step solutions. Understanding these examples will help reinforce the concepts and formulas discussed earlier.
Example 1: Perimeter of a Square
Given a square with a side length of \(4\) units, we can calculate its perimeter using the formula:
\[ \text{Perimeter} = 4 \times \text{side length} \]
Substituting the given side length:
\[ \text{Perimeter} = 4 \times 4 = 16 \text{ units} \]
Example 2: Perimeter of a Rectangle
Consider a rectangle with a length of \(7\) units and a width of \(3\) units. The formula to calculate the perimeter is:
\[ \text{Perimeter} = 2 \times (\text{length} + \text{width}) \]
Substituting the given dimensions:
\[ \text{Perimeter} = 2 \times (7 + 3) = 2 \times 10 = 20 \text{ units} \]
Example 3: Perimeter of an Irregular Polygon
For an irregular polygon with side lengths of \(5\) units, \(3\) units, \(7\) units, and \(4\) units, the perimeter is calculated by summing the lengths of all sides:
\[ \text{Perimeter} = 5 + 3 + 7 + 4 = 19 \text{ units} \]
Example 4: Perimeter of an Equilateral Triangle
Given an equilateral triangle with a perimeter of \(27\) units, we can find the length of one side. The formula for the perimeter of an equilateral triangle is:
\[ \text{Perimeter} = 3 \times \text{side length} \]
Rearranging the formula to solve for the side length:
\[ \text{side length} = \frac{\text{Perimeter}}{3} = \frac{27}{3} = 9 \text{ units} \]
Example 5: Finding a Missing Side Length
Consider a polygon with sides \(AB = 3\) units, \(BC = 4\) units, \(CD = 6\) units, \(DE = 2\) units, \(EF = 1.5\) units, and an unknown side \(FA\). Given that the perimeter of the polygon is \(18.5\) units, we can find the missing side \(FA\) by subtracting the sum of the known sides from the total perimeter:
\[ 18.5 = 3 + 4 + 6 + 2 + 1.5 + FA \]
\[ FA = 18.5 - (3 + 4 + 6 + 2 + 1.5) = 18.5 - 16.5 = 2 \text{ units} \]
Example 6: Perimeter of a Regular Pentagon
For a regular pentagon with a side length of \(5\) units, the perimeter is calculated as:
\[ \text{Perimeter} = 5 \times \text{side length} = 5 \times 5 = 25 \text{ units} \]
These examples illustrate how to apply the perimeter formulas to different types of polygons. By following these steps, you can confidently calculate the perimeter of any polygon you encounter.
Examples and Step-by-Step Solutions
In this section, we will explore a few examples that demonstrate how to calculate the perimeter of various polygons using step-by-step solutions. Understanding these examples will help reinforce the concepts and formulas discussed earlier.
Example 1: Perimeter of a Square
Given a square with a side length of \(4\) units, we can calculate its perimeter using the formula:
\[ \text{Perimeter} = 4 \times \text{side length} \]
Substituting the given side length:
\[ \text{Perimeter} = 4 \times 4 = 16 \text{ units} \]
Example 2: Perimeter of a Rectangle
Consider a rectangle with a length of \(7\) units and a width of \(3\) units. The formula to calculate the perimeter is:
\[ \text{Perimeter} = 2 \times (\text{length} + \text{width}) \]
Substituting the given dimensions:
\[ \text{Perimeter} = 2 \times (7 + 3) = 2 \times 10 = 20 \text{ units} \]
Example 3: Perimeter of an Irregular Polygon
For an irregular polygon with side lengths of \(5\) units, \(3\) units, \(7\) units, and \(4\) units, the perimeter is calculated by summing the lengths of all sides:
\[ \text{Perimeter} = 5 + 3 + 7 + 4 = 19 \text{ units} \]
Example 4: Perimeter of an Equilateral Triangle
Given an equilateral triangle with a perimeter of \(27\) units, we can find the length of one side. The formula for the perimeter of an equilateral triangle is:
\[ \text{Perimeter} = 3 \times \text{side length} \]
Rearranging the formula to solve for the side length:
\[ \text{side length} = \frac{\text{Perimeter}}{3} = \frac{27}{3} = 9 \text{ units} \]
Example 5: Finding a Missing Side Length
Consider a polygon with sides \(AB = 3\) units, \(BC = 4\) units, \(CD = 6\) units, \(DE = 2\) units, \(EF = 1.5\) units, and an unknown side \(FA\). Given that the perimeter of the polygon is \(18.5\) units, we can find the missing side \(FA\) by subtracting the sum of the known sides from the total perimeter:
\[ 18.5 = 3 + 4 + 6 + 2 + 1.5 + FA \]
\[ FA = 18.5 - (3 + 4 + 6 + 2 + 1.5) = 18.5 - 16.5 = 2 \text{ units} \]
Example 6: Perimeter of a Regular Pentagon
For a regular pentagon with a side length of \(5\) units, the perimeter is calculated as:
\[ \text{Perimeter} = 5 \times \text{side length} = 5 \times 5 = 25 \text{ units} \]
These examples illustrate how to apply the perimeter formulas to different types of polygons. By following these steps, you can confidently calculate the perimeter of any polygon you encounter.
Applications in Real Life
The concept of the perimeter of polygons has numerous practical applications in everyday life and various industries. Here are some key areas where perimeter calculations are essential:
-
Construction and Architecture:
In construction, the perimeter of land plots, buildings, and various structures is crucial for planning and laying foundations. For example, determining the amount of fencing required for a property or the border length of a garden involves calculating the perimeter. Builders and architects use these measurements to ensure that designs are accurate and materials are used efficiently.
-
Interior Design:
Interior designers use perimeter calculations to determine the lengths of materials needed for various elements such as baseboards, crown moldings, and wallpaper borders. Accurate perimeter measurements help in estimating costs and avoiding material wastage.
-
Landscaping:
Landscapers often need to calculate the perimeter of gardens, lawns, and other outdoor spaces to plan the installation of walkways, flower beds, and irrigation systems. Knowing the perimeter helps in efficiently distributing resources and creating aesthetically pleasing designs.
-
Sports Fields:
The perimeter of sports fields and courts, such as soccer fields, basketball courts, and running tracks, is used to install fencing, marking lines, and seating arrangements. Accurate perimeter measurements ensure that the fields are built to regulation sizes and specifications.
-
Urban Planning:
Urban planners use perimeter measurements in designing city layouts, zoning areas, and planning public spaces such as parks and recreational areas. This helps in efficient space utilization and infrastructure development.
-
Manufacturing:
In manufacturing, especially in the production of custom products like furniture, signage, and fabrications, knowing the perimeter of components helps in precise cutting and assembly. This ensures that parts fit together correctly and the final product meets design specifications.
-
Computer Graphics:
In computer graphics and video game design, polygons are used to create three-dimensional models and environments. Calculating the perimeter of these polygons helps in rendering detailed and accurate visual representations.
Overall, the ability to calculate the perimeter of polygons is an essential skill that aids in various practical and professional activities, making tasks more efficient and accurate.
Applications in Real Life
The concept of the perimeter of polygons has numerous practical applications in everyday life and various industries. Here are some key areas where perimeter calculations are essential:
-
Construction and Architecture:
In construction, the perimeter of land plots, buildings, and various structures is crucial for planning and laying foundations. For example, determining the amount of fencing required for a property or the border length of a garden involves calculating the perimeter. Builders and architects use these measurements to ensure that designs are accurate and materials are used efficiently.
-
Interior Design:
Interior designers use perimeter calculations to determine the lengths of materials needed for various elements such as baseboards, crown moldings, and wallpaper borders. Accurate perimeter measurements help in estimating costs and avoiding material wastage.
-
Landscaping:
Landscapers often need to calculate the perimeter of gardens, lawns, and other outdoor spaces to plan the installation of walkways, flower beds, and irrigation systems. Knowing the perimeter helps in efficiently distributing resources and creating aesthetically pleasing designs.
-
Sports Fields:
The perimeter of sports fields and courts, such as soccer fields, basketball courts, and running tracks, is used to install fencing, marking lines, and seating arrangements. Accurate perimeter measurements ensure that the fields are built to regulation sizes and specifications.
-
Urban Planning:
Urban planners use perimeter measurements in designing city layouts, zoning areas, and planning public spaces such as parks and recreational areas. This helps in efficient space utilization and infrastructure development.
-
Manufacturing:
In manufacturing, especially in the production of custom products like furniture, signage, and fabrications, knowing the perimeter of components helps in precise cutting and assembly. This ensures that parts fit together correctly and the final product meets design specifications.
-
Computer Graphics:
In computer graphics and video game design, polygons are used to create three-dimensional models and environments. Calculating the perimeter of these polygons helps in rendering detailed and accurate visual representations.
Overall, the ability to calculate the perimeter of polygons is an essential skill that aids in various practical and professional activities, making tasks more efficient and accurate.

Applications in Real Life
The concept of the perimeter of polygons has numerous practical applications in everyday life and various industries. Here are some key areas where perimeter calculations are essential:
-
Construction and Architecture:
In construction, the perimeter of land plots, buildings, and various structures is crucial for planning and laying foundations. For example, determining the amount of fencing required for a property or the border length of a garden involves calculating the perimeter. Builders and architects use these measurements to ensure that designs are accurate and materials are used efficiently.
-
Interior Design:
Interior designers use perimeter calculations to determine the lengths of materials needed for various elements such as baseboards, crown moldings, and wallpaper borders. Accurate perimeter measurements help in estimating costs and avoiding material wastage.
-
Landscaping:
Landscapers often need to calculate the perimeter of gardens, lawns, and other outdoor spaces to plan the installation of walkways, flower beds, and irrigation systems. Knowing the perimeter helps in efficiently distributing resources and creating aesthetically pleasing designs.
-
Sports Fields:
The perimeter of sports fields and courts, such as soccer fields, basketball courts, and running tracks, is used to install fencing, marking lines, and seating arrangements. Accurate perimeter measurements ensure that the fields are built to regulation sizes and specifications.
-
Urban Planning:
Urban planners use perimeter measurements in designing city layouts, zoning areas, and planning public spaces such as parks and recreational areas. This helps in efficient space utilization and infrastructure development.
-
Manufacturing:
In manufacturing, especially in the production of custom products like furniture, signage, and fabrications, knowing the perimeter of components helps in precise cutting and assembly. This ensures that parts fit together correctly and the final product meets design specifications.
-
Computer Graphics:
In computer graphics and video game design, polygons are used to create three-dimensional models and environments. Calculating the perimeter of these polygons helps in rendering detailed and accurate visual representations.
Overall, the ability to calculate the perimeter of polygons is an essential skill that aids in various practical and professional activities, making tasks more efficient and accurate.

Common Mistakes and How to Avoid Them
Calculating the perimeter of a polygon can sometimes lead to common mistakes. Here are some of the most frequent errors and how to avoid them:
- Misidentifying the Polygon Type:
It's crucial to correctly identify whether the polygon is regular or irregular. A regular polygon has all sides and angles equal, whereas an irregular polygon has sides and angles of different lengths. Ensure you apply the correct formula for the polygon type.
- Incorrectly Adding Side Lengths:
For irregular polygons, you need to sum the lengths of all sides accurately. Missing a side or adding the same side twice are common errors. Double-check each measurement and ensure all sides are included.
- Using Incorrect Units:
Always make sure that all side lengths are in the same unit before performing any calculations. Converting units incorrectly can lead to significant errors. For example, if some sides are measured in centimeters and others in meters, convert them all to the same unit first.
- Formula Misapplication for Regular Polygons:
For regular polygons, use the formula: \( \text{Perimeter} = n \times s \), where \( n \) is the number of sides and \( s \) is the length of one side. Applying this formula incorrectly or using the wrong values can lead to incorrect results.
- Neglecting the Use of Coordinate Geometry:
When dealing with polygons on a coordinate plane, use the distance formula: \( d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \) to find the lengths of sides. Not using this method can result in incorrect side lengths and thus an incorrect perimeter.
- Ignoring Special Cases:
Some polygons have special properties, such as symmetry or equal opposite sides. Leveraging these properties can simplify calculations and reduce errors. For instance, for a parallelogram, the opposite sides are equal, so you only need to measure two sides.
By being mindful of these common mistakes and carefully applying the appropriate methods and formulas, you can accurately calculate the perimeter of any polygon.
Common Mistakes and How to Avoid Them
Calculating the perimeter of a polygon can sometimes lead to common mistakes. Here are some of the most frequent errors and how to avoid them:
- Misidentifying the Polygon Type:
It's crucial to correctly identify whether the polygon is regular or irregular. A regular polygon has all sides and angles equal, whereas an irregular polygon has sides and angles of different lengths. Ensure you apply the correct formula for the polygon type.
- Incorrectly Adding Side Lengths:
For irregular polygons, you need to sum the lengths of all sides accurately. Missing a side or adding the same side twice are common errors. Double-check each measurement and ensure all sides are included.
- Using Incorrect Units:
Always make sure that all side lengths are in the same unit before performing any calculations. Converting units incorrectly can lead to significant errors. For example, if some sides are measured in centimeters and others in meters, convert them all to the same unit first.
- Formula Misapplication for Regular Polygons:
For regular polygons, use the formula: \( \text{Perimeter} = n \times s \), where \( n \) is the number of sides and \( s \) is the length of one side. Applying this formula incorrectly or using the wrong values can lead to incorrect results.
- Neglecting the Use of Coordinate Geometry:
When dealing with polygons on a coordinate plane, use the distance formula: \( d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \) to find the lengths of sides. Not using this method can result in incorrect side lengths and thus an incorrect perimeter.
- Ignoring Special Cases:
Some polygons have special properties, such as symmetry or equal opposite sides. Leveraging these properties can simplify calculations and reduce errors. For instance, for a parallelogram, the opposite sides are equal, so you only need to measure two sides.
By being mindful of these common mistakes and carefully applying the appropriate methods and formulas, you can accurately calculate the perimeter of any polygon.
Common Mistakes and How to Avoid Them
Calculating the perimeter of a polygon can sometimes lead to common mistakes. Here are some of the most frequent errors and how to avoid them:
- Misidentifying the Polygon Type:
It's crucial to correctly identify whether the polygon is regular or irregular. A regular polygon has all sides and angles equal, whereas an irregular polygon has sides and angles of different lengths. Ensure you apply the correct formula for the polygon type.
- Incorrectly Adding Side Lengths:
For irregular polygons, you need to sum the lengths of all sides accurately. Missing a side or adding the same side twice are common errors. Double-check each measurement and ensure all sides are included.
- Using Incorrect Units:
Always make sure that all side lengths are in the same unit before performing any calculations. Converting units incorrectly can lead to significant errors. For example, if some sides are measured in centimeters and others in meters, convert them all to the same unit first.
- Formula Misapplication for Regular Polygons:
For regular polygons, use the formula: \( \text{Perimeter} = n \times s \), where \( n \) is the number of sides and \( s \) is the length of one side. Applying this formula incorrectly or using the wrong values can lead to incorrect results.
- Neglecting the Use of Coordinate Geometry:
When dealing with polygons on a coordinate plane, use the distance formula: \( d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \) to find the lengths of sides. Not using this method can result in incorrect side lengths and thus an incorrect perimeter.
- Ignoring Special Cases:
Some polygons have special properties, such as symmetry or equal opposite sides. Leveraging these properties can simplify calculations and reduce errors. For instance, for a parallelogram, the opposite sides are equal, so you only need to measure two sides.
By being mindful of these common mistakes and carefully applying the appropriate methods and formulas, you can accurately calculate the perimeter of any polygon.
Advanced Topics and Further Reading
As you become more familiar with the basics of polygon perimeters, you may want to delve into more advanced topics that explore deeper mathematical concepts and applications. Here are some advanced topics and resources for further reading:
1. Perimeter of Complex and Irregular Polygons
For complex and irregular polygons, calculating the perimeter requires breaking down the shape into simpler components, using various mathematical tools and techniques:
- Coordinate Geometry: Using coordinates of the vertices to calculate distances between points with the distance formula \( d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \). This approach is particularly useful for polygons on a coordinate plane.
- Vector Analysis: Utilizing vector operations to find perimeter by summing the magnitudes of vectors representing the sides of the polygon.
2. Perimeter in Three Dimensions
Extending the concept of perimeter to three-dimensional shapes involves calculating the total edge length of polyhedra. For example:
- Cube: Perimeter of all edges can be calculated as \( 12 \times \text{edge length} \).
- Polyhedra: Using Euler's formula \( V - E + F = 2 \) (where \( V \) is the number of vertices, \( E \) is the number of edges, and \( F \) is the number of faces) to understand the structure and calculate total edge length.
3. Advanced Calculations for Specific Polygons
Exploring detailed calculations for specific types of polygons can deepen your understanding:
- Regular Polygons: The perimeter of a regular polygon with \( n \) sides of length \( s \) is \( P = n \times s \). Advanced topics include derivations using trigonometric identities.
- Irregular Polygons: Methods to approximate the perimeter using numerical integration when exact calculation is complex.
4. Algorithms and Computational Geometry
With the advent of computational tools, algorithms play a crucial role in perimeter calculations:
- Convex Hull Algorithms: Algorithms like Graham's scan or the Quickhull algorithm to determine the convex hull of a set of points, which helps in perimeter calculations.
- Polygon Clipping: Sutherland-Hodgman algorithm for clipping polygons, useful in computer graphics and GIS applications.
5. Real-World Applications and Problems
Understanding the perimeter of polygons has various practical applications:
- Urban Planning: Calculating the perimeter of land parcels for zoning and development.
- Robotics: Path planning algorithms in robotics use perimeter calculations to navigate around obstacles.
- Geospatial Analysis: Measuring the perimeter of geographic features for environmental and resource management.
Further Reading and Resources
To expand your knowledge, consider exploring the following resources:
- : Offers comprehensive lessons and exercises on perimeter and other geometric concepts.
- : Provides in-depth explanations and examples, including advanced perimeter calculations.
- : A practical tool for calculating perimeters and other properties of polygons.
Advanced Topics and Further Reading
As you become more familiar with the basics of polygon perimeters, you may want to delve into more advanced topics that explore deeper mathematical concepts and applications. Here are some advanced topics and resources for further reading:
1. Perimeter of Complex and Irregular Polygons
For complex and irregular polygons, calculating the perimeter requires breaking down the shape into simpler components, using various mathematical tools and techniques:
- Coordinate Geometry: Using coordinates of the vertices to calculate distances between points with the distance formula \( d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \). This approach is particularly useful for polygons on a coordinate plane.
- Vector Analysis: Utilizing vector operations to find perimeter by summing the magnitudes of vectors representing the sides of the polygon.
2. Perimeter in Three Dimensions
Extending the concept of perimeter to three-dimensional shapes involves calculating the total edge length of polyhedra. For example:
- Cube: Perimeter of all edges can be calculated as \( 12 \times \text{edge length} \).
- Polyhedra: Using Euler's formula \( V - E + F = 2 \) (where \( V \) is the number of vertices, \( E \) is the number of edges, and \( F \) is the number of faces) to understand the structure and calculate total edge length.
3. Advanced Calculations for Specific Polygons
Exploring detailed calculations for specific types of polygons can deepen your understanding:
- Regular Polygons: The perimeter of a regular polygon with \( n \) sides of length \( s \) is \( P = n \times s \). Advanced topics include derivations using trigonometric identities.
- Irregular Polygons: Methods to approximate the perimeter using numerical integration when exact calculation is complex.
4. Algorithms and Computational Geometry
With the advent of computational tools, algorithms play a crucial role in perimeter calculations:
- Convex Hull Algorithms: Algorithms like Graham's scan or the Quickhull algorithm to determine the convex hull of a set of points, which helps in perimeter calculations.
- Polygon Clipping: Sutherland-Hodgman algorithm for clipping polygons, useful in computer graphics and GIS applications.
5. Real-World Applications and Problems
Understanding the perimeter of polygons has various practical applications:
- Urban Planning: Calculating the perimeter of land parcels for zoning and development.
- Robotics: Path planning algorithms in robotics use perimeter calculations to navigate around obstacles.
- Geospatial Analysis: Measuring the perimeter of geographic features for environmental and resource management.
Further Reading and Resources
To expand your knowledge, consider exploring the following resources:
- : Offers comprehensive lessons and exercises on perimeter and other geometric concepts.
- : Provides in-depth explanations and examples, including advanced perimeter calculations.
- : A practical tool for calculating perimeters and other properties of polygons.
Advanced Topics and Further Reading
As you become more familiar with the basics of polygon perimeters, you may want to delve into more advanced topics that explore deeper mathematical concepts and applications. Here are some advanced topics and resources for further reading:
1. Perimeter of Complex and Irregular Polygons
For complex and irregular polygons, calculating the perimeter requires breaking down the shape into simpler components, using various mathematical tools and techniques:
- Coordinate Geometry: Using coordinates of the vertices to calculate distances between points with the distance formula \( d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \). This approach is particularly useful for polygons on a coordinate plane.
- Vector Analysis: Utilizing vector operations to find perimeter by summing the magnitudes of vectors representing the sides of the polygon.
2. Perimeter in Three Dimensions
Extending the concept of perimeter to three-dimensional shapes involves calculating the total edge length of polyhedra. For example:
- Cube: Perimeter of all edges can be calculated as \( 12 \times \text{edge length} \).
- Polyhedra: Using Euler's formula \( V - E + F = 2 \) (where \( V \) is the number of vertices, \( E \) is the number of edges, and \( F \) is the number of faces) to understand the structure and calculate total edge length.
3. Advanced Calculations for Specific Polygons
Exploring detailed calculations for specific types of polygons can deepen your understanding:
- Regular Polygons: The perimeter of a regular polygon with \( n \) sides of length \( s \) is \( P = n \times s \). Advanced topics include derivations using trigonometric identities.
- Irregular Polygons: Methods to approximate the perimeter using numerical integration when exact calculation is complex.
4. Algorithms and Computational Geometry
With the advent of computational tools, algorithms play a crucial role in perimeter calculations:
- Convex Hull Algorithms: Algorithms like Graham's scan or the Quickhull algorithm to determine the convex hull of a set of points, which helps in perimeter calculations.
- Polygon Clipping: Sutherland-Hodgman algorithm for clipping polygons, useful in computer graphics and GIS applications.
5. Real-World Applications and Problems
Understanding the perimeter of polygons has various practical applications:
- Urban Planning: Calculating the perimeter of land parcels for zoning and development.
- Robotics: Path planning algorithms in robotics use perimeter calculations to navigate around obstacles.
- Geospatial Analysis: Measuring the perimeter of geographic features for environmental and resource management.
Further Reading and Resources
To expand your knowledge, consider exploring the following resources:
- : Offers comprehensive lessons and exercises on perimeter and other geometric concepts.
- : Provides in-depth explanations and examples, including advanced perimeter calculations.
- : A practical tool for calculating perimeters and other properties of polygons.
Video hướng dẫn cách tính chu vi của các loại đa giác, giúp bạn nắm vững kiến thức toán học cơ bản.
Cách tính chu vi đa giác: Hướng dẫn chi tiết
READ MORE:
Video hướng dẫn cách tính chu vi của bất kỳ đa giác nào, cung cấp phương pháp chi tiết và dễ hiểu.
Chu vi - Tìm chu vi của bất kỳ đa giác nào