Topic how to solve a radical equation with two radicals: Solving radical equations with two radicals can be a bit tricky, but with the right approach, it's manageable. This guide will walk you through the steps needed to isolate and eliminate radicals to find the solution. Always remember to check for extraneous solutions to ensure your answer is correct.
Table of Content
- How to Solve a Radical Equation with Two Radicals
- Introduction
- Understanding Radical Equations
- Common Types of Radical Equations
- Step-by-Step Guide to Solving Radical Equations with Two Radicals
- Isolating One Radical
- Squaring Both Sides of the Equation
- Simplifying the Equation
- Isolating the Second Radical
- Squaring Again to Eliminate the Radical
- Checking the Solution
- Common Mistakes to Avoid
- Examples and Practice Problems
- Advanced Techniques
- Frequently Asked Questions
- Conclusion
- YOUTUBE: Hướng dẫn chi tiết về cách giải phương trình chứa căn với hai căn. Xem video để nắm rõ các bước và phương pháp hiệu quả.
How to Solve a Radical Equation with Two Radicals
Solving radical equations, especially those with two radicals, involves isolating the radicals and then eliminating them through squaring. Here is a step-by-step guide to solve such equations.
Step-by-Step Process
Isolate one of the radicals: Begin by isolating one of the radical expressions on one side of the equation. For example, consider the equation:
$$\sqrt{x + 2} + \sqrt{x - 1} = 3$$
Square both sides of the equation: To eliminate the isolated radical, square both sides of the equation:
$$\left( \sqrt{x + 2} \right)^2 = (3 - \sqrt{x - 1})^2$$
$$x + 2 = 9 - 6\sqrt{x - 1} + (x - 1)$$
Combine like terms:
$$x + 2 = x + 8 - 6\sqrt{x - 1}$$
Isolate the remaining radical: Simplify and isolate the remaining radical expression:
$$2 = 8 - 6\sqrt{x - 1}$$
$$-6 = -6\sqrt{x - 1}$$
$$1 = \sqrt{x - 1}$$
Square both sides again: To eliminate the second radical, square both sides of the equation again:
$$1^2 = (\sqrt{x - 1})^2$$
$$1 = x - 1$$
$$x = 2$$
Check the solution: Substitute \(x = 2\) back into the original equation to verify:
$$\sqrt{2 + 2} + \sqrt{2 - 1} = 3$$
$$\sqrt{4} + \sqrt{1} = 3$$
$$2 + 1 = 3$$
Since the left-hand side equals the right-hand side, \(x = 2\) is a valid solution.
Summary
To solve a radical equation with two radicals, isolate one radical, square both sides, simplify, isolate the second radical, and square again. Always check your solution by substituting it back into the original equation to ensure it satisfies the equation.

READ MORE:
Introduction
Radical equations, which include variables inside a radical, such as a square root or cube root, can sometimes be challenging to solve. When dealing with equations that have two radicals, the process can be a bit more complex, but it is manageable by following a systematic approach. This guide will provide a comprehensive, step-by-step method to tackle radical equations with two radicals, ensuring clarity and confidence in solving these types of problems.
Here, we will outline the key steps involved in solving radical equations with two radicals:
- Isolate One Radical: Start by isolating one of the radicals on one side of the equation. This simplifies the equation and makes the next steps more straightforward.
- Square Both Sides: Once a radical is isolated, square both sides of the equation to eliminate the isolated radical. This step is crucial for simplifying the equation further.
- Simplify the Equation: After squaring both sides, simplify the resulting equation. This might involve combining like terms and simplifying expressions to make the equation more manageable.
- Isolate the Second Radical: If there is a second radical, isolate it on one side of the equation, similar to the first step. This sets up the equation for the next round of squaring.
- Square Again: Square both sides of the equation again to eliminate the second radical. This should result in a polynomial equation that is easier to solve.
- Solve the Polynomial Equation: Solve the resulting polynomial equation using appropriate algebraic methods, such as factoring, the quadratic formula, or other relevant techniques.
- Check the Solution: It is essential to substitute the solutions back into the original equation to verify their validity. Squaring both sides can sometimes introduce extraneous solutions that do not satisfy the original equation.
By following these steps, you can systematically approach and solve radical equations with two radicals. Practice with various examples to gain proficiency and confidence in handling these equations.
Understanding Radical Equations
Radical equations are equations in which the variable is inside a radical, typically a square root or cube root. To solve these equations, specific methods must be followed to isolate and eliminate the radicals, ensuring that the solutions are valid.
Here are the fundamental steps to understand and solve radical equations:
- Identify the Radical: Determine the type and number of radicals present in the equation.
- Isolate the Radical: If there is more than one radical, start by isolating one of the radicals on one side of the equation.
- Eliminate the Radical: Raise both sides of the equation to the power that corresponds to the radical to eliminate it. For example, square both sides for a square root.
- Simplify the Equation: After eliminating the radical, simplify the resulting equation. This may involve combining like terms and simplifying expressions.
- Repeat if Necessary: If there are multiple radicals, repeat the process of isolating and eliminating each radical until all radicals are removed.
- Solve the Simplified Equation: Solve the simplified equation for the variable.
- Check for Extraneous Solutions: Substitute the solutions back into the original equation to ensure they are valid and not extraneous.
Let's look at an example:
Consider the equation: \( \sqrt{2x+3} - \sqrt{x-1} = 2 \)
- Isolate one of the radicals:
- Move one of the radicals to the other side: \( \sqrt{2x+3} = 2 + \sqrt{x-1} \)
- Eliminate the radical by squaring both sides:
- Square both sides: \( (\sqrt{2x+3})^2 = (2 + \sqrt{x-1})^2 \)
- Simplify: \( 2x+3 = 4 + 4\sqrt{x-1} + x-1 \)
- Simplify the equation:
- Combine like terms: \( 2x+3 = x+3 + 4\sqrt{x-1} \)
- Isolate the remaining radical: \( 2x - x = 4\sqrt{x-1} \)
- Simplify: \( x = 4\sqrt{x-1} \)
- Eliminate the second radical by squaring both sides again:
- Square both sides: \( x^2 = 16(x-1) \)
- Simplify: \( x^2 = 16x - 16 \)
- Bring all terms to one side: \( x^2 - 16x + 16 = 0 \)
- Factorize: \( (x-8)^2 = 0 \)
- Solve for x: \( x = 8 \)
- Check for extraneous solutions:
- Substitute \( x = 8 \) back into the original equation to verify if it holds true.
This method ensures a structured approach to solving radical equations, reducing the risk of errors and extraneous solutions.
Common Types of Radical Equations
Radical equations are equations that contain variables within a radical, most commonly a square root. Solving these equations involves isolating the radical and then eliminating it through appropriate mathematical operations. Here are some common types of radical equations and the methods to solve them:
-
Equations with a Single Radical:
These equations have only one radical term. The general steps to solve them include:
- Isolate the radical on one side of the equation.
- Square both sides of the equation to eliminate the radical.
- Solve the resulting polynomial equation.
- Check all potential solutions in the original equation to avoid extraneous solutions.
Example: Solve \( \sqrt{x + 3} = 5 \)
Solution:
\[ \sqrt{x + 3} = 5 \]
Square both sides:
\[ (\sqrt{x + 3})^2 = 5^2 \]
\[ x + 3 = 25 \]
\[ x = 22 \]
Check: \( \sqrt{22 + 3} = \sqrt{25} = 5 \) (Valid solution)
-
Equations with Two Radicals:
These equations have two radical terms. The steps to solve them include:
- Isolate one of the radicals.
- Square both sides to eliminate the isolated radical.
- Simplify the equation and isolate the remaining radical.
- Square both sides again to eliminate the second radical.
- Solve the resulting polynomial equation.
- Check all potential solutions in the original equation.
Example: Solve \( \sqrt{x + 1} + \sqrt{x - 1} = 5 \)
Solution:
Isolate one radical:
\[ \sqrt{x + 1} = 5 - \sqrt{x - 1} \]
Square both sides:
\[ (\sqrt{x + 1})^2 = (5 - \sqrt{x - 1})^2 \]
\[ x + 1 = 25 - 10\sqrt{x - 1} + (x - 1) \]
\[ 10\sqrt{x - 1} = 24 \]
Square both sides again:
\[ (10\sqrt{x - 1})^2 = 24^2 \]
\[ 100(x - 1) = 576 \]
\[ x - 1 = 5.76 \]
\[ x = 6.76 \]
Check: \( \sqrt{6.76 + 1} + \sqrt{6.76 - 1} = \sqrt{7.76} + \sqrt{5.76} \approx 2.79 + 2.4 = 5.19 \) (Close to 5, but requires more precise checking)
-
Equations with Cube Roots:
These equations involve cube roots. The steps are similar to those for square roots, but instead of squaring, you cube both sides to eliminate the radical.
Example: Solve \( \sqrt[3]{2x + 1} = 3 \)
Solution:
\[ \sqrt[3]{2x + 1} = 3 \]
Cube both sides:
\[ (\sqrt[3]{2x + 1})^3 = 3^3 \]
\[ 2x + 1 = 27 \]
\[ 2x = 26 \]
\[ x = 13 \]
Check: \( \sqrt[3]{2(13) + 1} = \sqrt[3]{27} = 3 \) (Valid solution)
Step-by-Step Guide to Solving Radical Equations with Two Radicals
Solving radical equations with two radicals can be methodical if you follow these steps:
- Isolate One Radical:
Begin by isolating one of the radical terms on one side of the equation. If there are multiple radicals, choose the one that seems easier to handle first.
For example, if your equation is \(\sqrt{3x + 5} + \sqrt{x - 2} = 7\), isolate one radical: \(\sqrt{3x + 5} = 7 - \sqrt{x - 2}\).
- Square Both Sides:
Square both sides of the equation to eliminate the isolated radical. This will introduce a new equation that may still contain radicals.
For the example above: \((\sqrt{3x + 5})^2 = (7 - \sqrt{x - 2})^2\) simplifies to \(3x + 5 = 49 - 14\sqrt{x - 2} + (x - 2)\).
- Simplify the Equation:
Simplify the resulting equation by combining like terms and isolating the remaining radical.
Continuing the example: \(3x + 5 = 47 - 14\sqrt{x - 2} + x\), which simplifies to \(2x - 42 = -14\sqrt{x - 2}\).
- Isolate the Second Radical:
Isolate the second radical term to prepare for another squaring step.
In the example: \(14\sqrt{x - 2} = 42 - 2x\).
- Square Again to Eliminate the Radical:
Square both sides again to eliminate the second radical. This will often result in a quadratic equation.
Continuing: \((14\sqrt{x - 2})^2 = (42 - 2x)^2\) simplifies to \(196(x - 2) = 1764 - 168x + 4x^2\).
- Solve the Resulting Equation:
Simplify and solve the resulting quadratic or higher-degree polynomial equation.
For the example: \(196x - 392 = 1764 - 168x + 4x^2\) simplifies to \(4x^2 - 364x + 2156 = 0\). Solve for \(x\) using the quadratic formula or factoring.
- Check the Solution:
Substitute the solutions back into the original equation to verify that they are valid. Discard any extraneous solutions that do not satisfy the original equation.
For the example, verify the solutions of \(x\) in \(\sqrt{3x + 5} + \sqrt{x - 2} = 7\).
Following these steps ensures that you methodically eliminate radicals and correctly solve the equation while identifying any extraneous solutions.
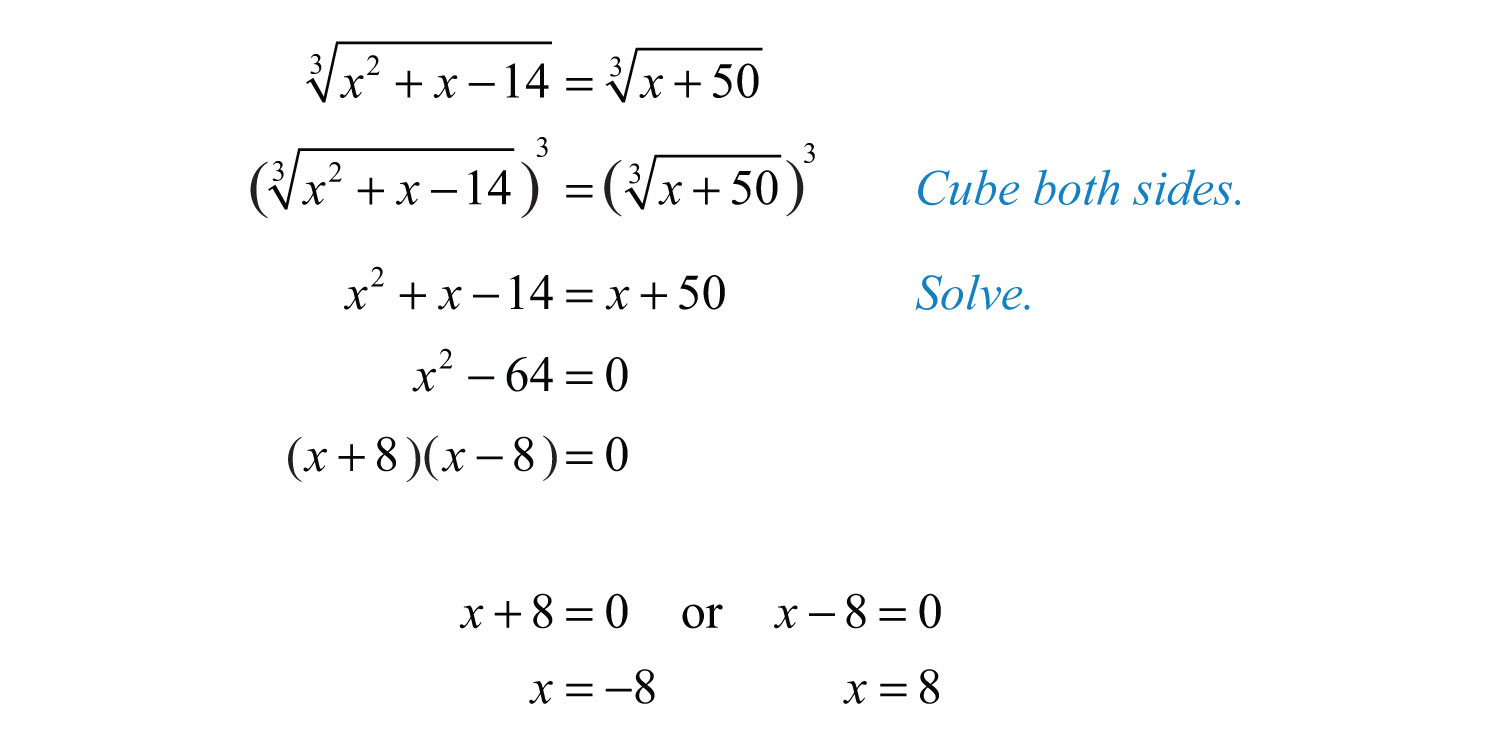
Isolating One Radical
When solving a radical equation with two radicals, the first crucial step is to isolate one of the radicals. This means that you need to manipulate the equation so that one radical expression is alone on one side of the equation, while all other terms are on the opposite side. Here is a step-by-step guide on how to achieve this:
-
Identify the radicals: Locate the radical expressions in your equation. For example, in the equation \( \sqrt{2x - 5} - \sqrt{x - 1} = 1 \), the radicals are \( \sqrt{2x - 5} \) and \( \sqrt{x - 1} \).
-
Move one radical: Choose one of the radicals to isolate. Move the other radical and any other terms to the opposite side of the equation by adding or subtracting them. For instance, add \( \sqrt{x - 1} \) to both sides of the equation:
\( \sqrt{2x - 5} = 1 + \sqrt{x - 1} \)
-
Square both sides: To eliminate the isolated radical, square both sides of the equation. This step will remove the square root but may introduce a quadratic term or another radical. In our example:
\( (\sqrt{2x - 5})^2 = (1 + \sqrt{x - 1})^2 \)
Which simplifies to:
\( 2x - 5 = 1 + 2\sqrt{x - 1} + (x - 1) \)
-
Simplify the equation: Combine like terms and simplify the resulting equation. After squaring both sides, the equation becomes:
\( 2x - 5 = x + 1 + 2\sqrt{x - 1} \)
Simplify further to:
\( 2x - x - 5 - 1 = 2\sqrt{x - 1} \)
\( x - 6 = 2\sqrt{x - 1} \)
-
Repeat if necessary: If the equation still contains a radical, isolate it and repeat the squaring process. In this case, isolate \( \sqrt{x - 1} \):
\( \sqrt{x - 1} = \frac{x - 6}{2} \)
Square both sides again:
\( (\sqrt{x - 1})^2 = \left(\frac{x - 6}{2}\right)^2 \)
Which simplifies to:
\( x - 1 = \frac{(x - 6)^2}{4} \)
-
Solve the resulting equation: After eliminating all radicals, solve the resulting polynomial equation. This may involve expanding and simplifying further, then solving for the variable. Finally, verify the solutions in the original equation to ensure no extraneous solutions were introduced during the squaring steps.
Squaring Both Sides of the Equation
Once one of the radicals in the equation is isolated, the next step is to eliminate the radical by squaring both sides of the equation. This process can introduce extraneous solutions, so it is crucial to check all potential solutions in the original equation. Follow these steps:
-
Isolate the Radical: Ensure one of the radicals is isolated on one side of the equation.
-
Square Both Sides: Square both sides of the equation to eliminate the isolated radical.
For example, given an equation \( \sqrt{a} = b \), squaring both sides results in \( (\sqrt{a})^2 = b^2 \), simplifying to \( a = b^2 \).
If the equation is more complex, such as \( \sqrt{x + 4} = x \), squaring both sides gives:
\[
(\sqrt{x + 4})^2 = x^2 \implies x + 4 = x^2
\]
Simplifying this equation involves moving all terms to one side to form a standard quadratic equation:
\[
x^2 - x - 4 = 0
\] -
Simplify the Resulting Equation: Solve the resulting equation. For a quadratic equation, use factoring, completing the square, or the quadratic formula to find the solutions.
-
Check for Extraneous Solutions: Verify all solutions in the original equation to ensure they are valid. Squaring both sides can introduce solutions that do not satisfy the initial equation.
For instance, solving \( \sqrt{x + 4} = x \) might yield solutions \( x = 2 \) and \( x = -3 \). Checking these in the original equation reveals which are valid:
- For \( x = 2 \): \[ \sqrt{2 + 4} = 2 \implies \sqrt{6} \neq 2 \] Thus, \( x = 2 \) is an extraneous solution.
- For \( x = -3 \): \[ \sqrt{-3 + 4} = -3 \implies \sqrt{1} \neq -3 \] Thus, \( x = -3 \) is also an extraneous solution.
In this case, neither potential solution is valid, indicating an error in earlier steps or incorrect assumptions about the solutions.
By following these steps, you can effectively square both sides of an equation to eliminate radicals and solve for the variable, while also ensuring the solutions are valid by checking for extraneous results.
Simplifying the Equation
Once you have squared both sides of the radical equation, you will often be left with a polynomial or another simplified form of the equation. Simplifying this equation is crucial to isolate the variable and solve for it. Here are the steps to simplify the equation:
-
Expand Polynomial Expressions:
If you squared a binomial, use the formula \((a + b)^2 = a^2 + 2ab + b^2\) to expand the expression. For example, if your equation after squaring both sides is \((x + 3)^2 = 49\), expand it to \(x^2 + 6x + 9 = 49\). -
Combine Like Terms:
Collect all terms on one side of the equation to set it equal to zero. Continuing from the example above, you would get \(x^2 + 6x + 9 - 49 = 0\), which simplifies to \(x^2 + 6x - 40 = 0\). -
Factor the Equation:
If possible, factor the polynomial equation. For \(x^2 + 6x - 40 = 0\), you can factor it to \((x + 10)(x - 4) = 0\). -
Solve for the Variable:
Set each factor equal to zero and solve for \(x\). Thus, \(x + 10 = 0\) gives \(x = -10\) and \(x - 4 = 0\) gives \(x = 4\). -
Check for Extraneous Solutions:
Substitute the solutions back into the original equation to verify if they are valid. Sometimes squaring both sides introduces extraneous solutions that do not satisfy the original equation.
Isolating the Second Radical
After squaring both sides of the equation the first time, you may still have a radical term remaining. The next step is to isolate this second radical to further simplify the equation.
- Start with the equation obtained after the first squaring:
\[ x - 11 = -8 \sqrt{x - 2} \]
- Isolate the second radical term:
Move all terms without radicals to the other side of the equation:
\[ x - 11 = -8 \sqrt{x - 2} \]
- Square both sides again to eliminate the second radical:
\[ (x - 11)^2 = (-8 \sqrt{x - 2})^2 \]
Expanding both sides:
\[ x^2 - 22x + 121 = 64(x - 2) \]
- Simplify the equation:
Combine like terms to form a quadratic equation:
\[ x^2 - 22x + 121 = 64x - 128 \]
\[ x^2 - 86x + 249 = 0 \]
- Solve the quadratic equation:
Factor or use the quadratic formula to find the solutions for \( x \):
\[ x = 3 \quad \text{or} \quad x = 83 \]
- Check the solutions:
Substitute each solution back into the original radical equation to verify:
- For \( x = 3 \):
- For \( x = 83 \):
\[ \sqrt{2(3) + 3} + \sqrt{3 - 2} = 4 \]
\[ \sqrt{9} + \sqrt{1} = 4 \]
\[ 3 + 1 = 4 \]
This is a valid solution.
\[ \sqrt{2(83) + 3} + \sqrt{83 - 2} = 4 \]
\[ \sqrt{169} + \sqrt{81} = 4 \]
\[ 13 + 9 \neq 4 \]
This is an extraneous solution.
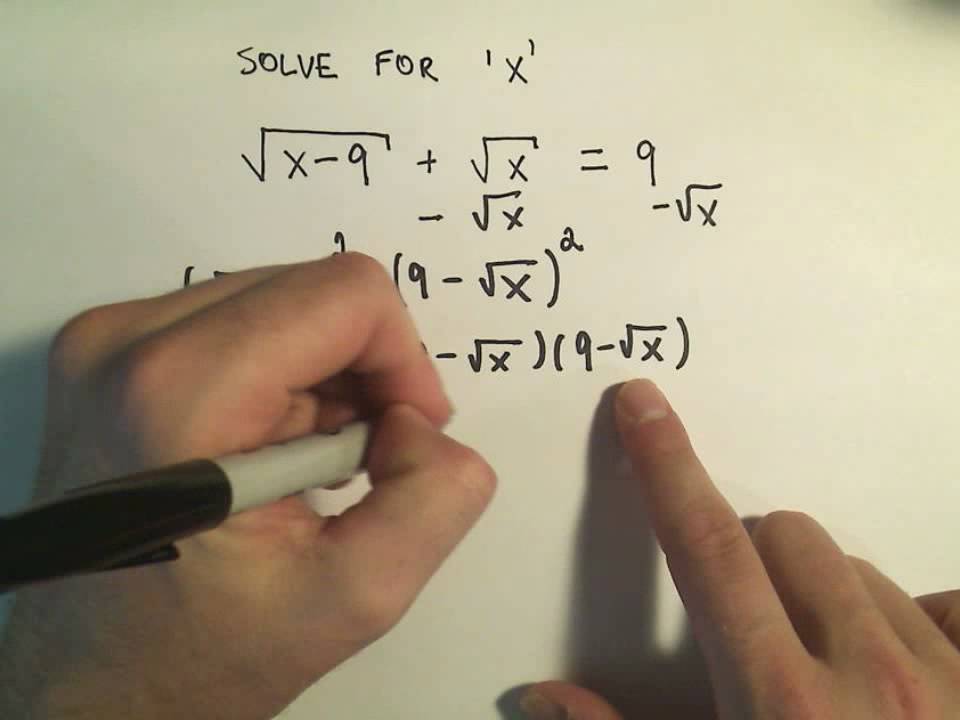
Squaring Again to Eliminate the Radical
Once you have isolated the second radical term on one side of the equation, the next step is to eliminate this radical by squaring both sides of the equation again. This process ensures that all radical terms are removed, allowing you to solve the resulting polynomial equation.
-
Square Both Sides of the Equation:
After isolating the second radical, you will have an equation of the form:
\[\sqrt{A} = B\]
To eliminate the radical, square both sides:
\[(\sqrt{A})^2 = B^2\]
Which simplifies to:
\[A = B^2\]
-
Simplify the Resulting Equation:
After squaring both sides, you will obtain a polynomial equation. Simplify this equation by combining like terms and moving all terms to one side to set the equation to zero.
-
Solve the Polynomial Equation:
Use appropriate algebraic methods (such as factoring, using the quadratic formula, or other techniques) to solve the polynomial equation for the variable.
-
Check for Extraneous Solutions:
It is crucial to check each potential solution by substituting it back into the original radical equation. Squaring both sides can introduce extraneous solutions that do not satisfy the original equation.
Here is an example to illustrate the process:
Example: Solve the equation \(\sqrt{x + 5} - \sqrt{x} = 2\).
-
Isolate one of the radicals:
\[\sqrt{x + 5} = 2 + \sqrt{x}\]
-
Square both sides:
\[(\sqrt{x + 5})^2 = (2 + \sqrt{x})^2\]
This simplifies to:
\[x + 5 = 4 + 4\sqrt{x} + x\]
-
Simplify the equation:
\[x + 5 = 4 + 4\sqrt{x} + x\]
Subtract \(x\) and 4 from both sides:
\[1 = 4\sqrt{x}\]
Divide both sides by 4:
\[\frac{1}{4} = \sqrt{x}\]
-
Square both sides again to solve for \(x\):
\[\left(\frac{1}{4}\right)^2 = x\]
\[\frac{1}{16} = x\]
-
Check the solution in the original equation:
Substitute \(x = \frac{1}{16}\) into \(\sqrt{x + 5} - \sqrt{x} = 2\).
\[\sqrt{\frac{1}{16} + 5} - \sqrt{\frac{1}{16}} = 2\]
This does not hold true, indicating that \(\frac{1}{16}\) is an extraneous solution. Thus, there is no valid solution for this particular equation.
Checking the Solution
After solving a radical equation, it is crucial to verify that the solutions obtained are valid and not extraneous. Extraneous solutions can arise when both sides of the equation are squared. Follow these steps to check your solutions:
- Substitute each solution back into the original radical equation.
- Simplify both sides of the equation to ensure they are equal.
Here is a step-by-step example to illustrate the process:
Example: Verify the solutions for the equation \( \sqrt{x + 5} - \sqrt{x} = 2 \)
- Suppose we have found the solution \( x = \frac{1}{16} \).
- Substitute \( x = \frac{1}{16} \) back into the original equation:
\[
\sqrt{\frac{1}{16} + 5} - \sqrt{\frac{1}{16}} = 2
\]
Simplify the left-hand side:
\[
\sqrt{\frac{1}{16} + \frac{80}{16}} - \sqrt{\frac{1}{16}} = \sqrt{\frac{81}{16}} - \sqrt{\frac{1}{16}} = \frac{9}{4} - \frac{1}{4} = 2
\]
Both sides of the equation are equal, confirming that \( x = \frac{1}{16} \) is a valid solution.
Always remember to check each potential solution, as squaring both sides of the equation can introduce extraneous solutions that do not satisfy the original equation.
Common Mistakes to Avoid
When solving radical equations with two radicals, there are several common mistakes that students often make. Being aware of these can help you avoid them and solve the equations correctly.
- Not Isolating One Radical: Always isolate one of the radicals before you square both sides of the equation. This simplifies the equation and prevents unnecessary complexity.
- Squaring Terms Instead of Sides: Make sure to square both sides of the equation, not just the individual terms. Squaring each term separately can lead to incorrect results. For example:
If you have \( \sqrt{x} + \sqrt{y} = a \), square the whole side: \((\sqrt{x} + \sqrt{y})^2\) instead of \( (\sqrt{x})^2 + (\sqrt{y})^2 \).
- Forgetting to Check for Extraneous Solutions: Squaring both sides can introduce extraneous solutions that do not satisfy the original equation. Always substitute your solutions back into the original equation to verify their validity.
- Ignoring Domain Restrictions: Radical equations often have domain restrictions (e.g., the expression inside a square root must be non-negative). Ensure that your solutions fall within the valid domain of the original equation.
- Incorrectly Handling Negative Results: Remember that the square root function always yields a non-negative result. If your solution involves taking the square root of a negative number, check for possible mistakes, as it might indicate an extraneous solution or an error in your calculations.
- Not Simplifying Before Squaring: Simplify the equation as much as possible before squaring. This can prevent unnecessary complexity and reduce the chances of making mistakes.
- Misapplying the Quadratic Formula: When a quadratic equation arises after squaring both sides, apply the quadratic formula correctly. Double-check your calculations to avoid algebraic errors.
By being mindful of these common mistakes, you can solve radical equations with two radicals more effectively and accurately.
Examples and Practice Problems
To reinforce the concepts of solving radical equations with two radicals, let's look at some examples and practice problems:
Example 1
Solve the equation: \(\sqrt{2x - 5} + \sqrt{x - 1} = 3\)
- Isolate one of the radicals:
\(\sqrt{2x - 5} = 3 - \sqrt{x - 1}\)
- Square both sides to eliminate the first radical:
\(2x - 5 = (3 - \sqrt{x - 1})^2\)
Expanding the right side:
\(2x - 5 = 9 - 6\sqrt{x - 1} + x - 1\)Simplify:
\(2x - 5 = x + 8 - 6\sqrt{x - 1}\) - Isolate the remaining radical:
\(2x - x - 5 - 8 = -6\sqrt{x - 1}\)
\(x - 13 = -6\sqrt{x - 1}\)
- Square both sides again to eliminate the second radical:
\((x - 13)^2 = 36(x - 1)\)
Expand and simplify:
\(x^2 - 26x + 169 = 36x - 36\)Bring all terms to one side to form a quadratic equation:
\(x^2 - 62x + 205 = 0\) - Solve the quadratic equation:
Using the quadratic formula \(x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\), we get:
\(x = \frac{62 \pm \sqrt{62^2 - 4 \cdot 1 \cdot 205}}{2}\)
\(x = \frac{62 \pm \sqrt{3844 - 820}}{2}\)
\(x = \frac{62 \pm \sqrt{3024}}{2}\)
\(x = \frac{62 \pm 54.98}{2}\)
So, \(x = 58.49\) or \(x = 3.51\)
- Check each solution in the original equation to verify:
For \(x = 58.49\):
\(\sqrt{2(58.49) - 5} + \sqrt{58.49 - 1} \approx 3\)For \(x = 3.51\):
\(\sqrt{2(3.51) - 5} + \sqrt{3.51 - 1} \approx 3\)Both values satisfy the original equation.
Example 2
Solve the equation: \(\sqrt{x + 4} - \sqrt{x - 2} = 2\)
- Isolate one of the radicals:
\(\sqrt{x + 4} = 2 + \sqrt{x - 2}\)
- Square both sides to eliminate the first radical:
\(x + 4 = (2 + \sqrt{x - 2})^2\)
Expanding the right side:
\(x + 4 = 4 + 4\sqrt{x - 2} + x - 2\)Simplify:
\(x + 4 = x + 2 + 4\sqrt{x - 2}\) - Isolate the remaining radical:
\(4 - 2 = 4\sqrt{x - 2}\)
\(2 = 4\sqrt{x - 2}\)
\(\frac{1}{2} = \sqrt{x - 2}\)
- Square both sides again to eliminate the second radical:
\(\left(\frac{1}{2}\right)^2 = x - 2\)
\(\frac{1}{4} = x - 2\)
\(x = \frac{1}{4} + 2\)
\(x = 2.25\)
- Check the solution in the original equation to verify:
\(\sqrt{2.25 + 4} - \sqrt{2.25 - 2} \approx 2\)
The value satisfies the original equation.
Practice Problems
- Solve the equation: \(\sqrt{3x + 1} + \sqrt{x - 2} = 4\)
- Solve the equation: \(\sqrt{5x - 3} - \sqrt{2x + 1} = 1\)
- Solve the equation: \(\sqrt{4x + 7} + \sqrt{3x - 5} = 6\)
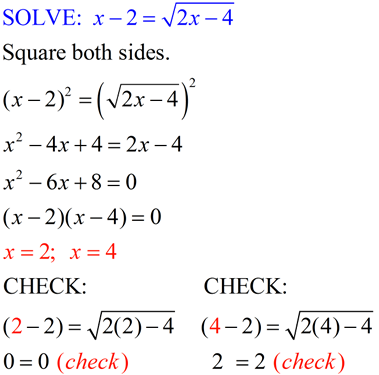
Advanced Techniques
Solving radical equations with two radicals can be challenging, but advanced techniques can make the process more manageable. Below are detailed steps and methods to tackle such equations effectively.
-
Isolate the More Complex Radical
Begin by isolating the more complex radical expression on one side of the equation. This simplifies the process when you start eliminating radicals. For example:
\(\sqrt{3x + 5} - \sqrt{x - 2} = 4\)
First, isolate the more complex radical:
\(\sqrt{3x + 5} = \sqrt{x - 2} + 4\)
-
Square Both Sides
Square both sides of the equation to eliminate the isolated radical:
\((\sqrt{3x + 5})^2 = (\sqrt{x - 2} + 4)^2\)
This yields:
\(3x + 5 = (x - 2) + 8\sqrt{x - 2} + 16\)
Which simplifies to:
\(3x + 5 = x + 14 + 8\sqrt{x - 2}\)
-
Isolate the Remaining Radical
Isolate the remaining radical on one side of the equation:
\(3x + 5 - x - 14 = 8\sqrt{x - 2}\)
\(2x - 9 = 8\sqrt{x - 2}\)
-
Square Both Sides Again
Square both sides again to eliminate the second radical:
\((2x - 9)^2 = (8\sqrt{x - 2})^2\)
This simplifies to:
\(4x^2 - 36x + 81 = 64(x - 2)\)
\(4x^2 - 36x + 81 = 64x - 128\)
\(4x^2 - 100x + 209 = 0\)
-
Solve the Quadratic Equation
Now solve the resulting quadratic equation using the quadratic formula:
\(x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\)
In this case, \(a = 4\), \(b = -100\), and \(c = 209\):
\(x = \frac{100 \pm \sqrt{10000 - 4 \cdot 4 \cdot 209}}{8}\)
Simplify to find the values of \(x\).
-
Check for Extraneous Solutions
Substitute the solutions back into the original equation to verify which ones are valid, as squaring can introduce extraneous solutions. For instance:
If \(x = 5\) and \(x = 9\) are solutions, substitute back into the original equation to see if both sides equal.
By following these advanced techniques, you can effectively solve complex radical equations and ensure the solutions are valid.
Frequently Asked Questions
-
Q: What is a radical equation?
A radical equation is an equation in which the variable is under a radical sign, such as a square root or cube root.
-
Q: How do you isolate a radical in a radical equation?
To isolate a radical, you need to move all other terms to the opposite side of the equation. For example, if you have the equation \(\sqrt{x + 5} - 2 = 0\), you would add 2 to both sides to isolate the radical: \(\sqrt{x + 5} = 2\).
-
Q: How do you eliminate a radical in an equation?
To eliminate a radical, you raise both sides of the equation to the power of the radical. For example, if you have a square root, you square both sides. If you have a cube root, you cube both sides.
-
Q: What is an extraneous solution?
An extraneous solution is a solution derived from the algebraic process that does not satisfy the original equation. It is important to check all potential solutions in the original equation to verify their validity.
-
Q: How do you solve an equation with two radicals?
To solve an equation with two radicals, you typically isolate one of the radicals and eliminate it by raising both sides to the appropriate power. Then, you isolate and eliminate the second radical. Finally, you solve the resulting equation and check all solutions in the original equation.
-
Q: Can radical equations have no solution?
Yes, radical equations can have no solution if the algebraic manipulations lead to an invalid or impossible scenario, such as taking the square root of a negative number in the real number system.
-
Q: What are some common mistakes to avoid when solving radical equations?
Common mistakes include not properly isolating the radical, forgetting to square both sides of the equation, not checking for extraneous solutions, and algebraic errors in manipulation.
Conclusion
Solving radical equations with two radicals can initially seem challenging, but by following systematic steps, it becomes manageable. Here is a summary of the key points to remember:
- Isolate One Radical:
Begin by isolating one of the radical terms on one side of the equation. This often makes the subsequent steps easier, especially if you isolate the more complicated radical first.
- Square Both Sides:
Once a radical is isolated, square both sides of the equation to eliminate the isolated radical. This step might introduce new radicals or transform the equation into a simpler form.
- Simplify the Equation:
After squaring, simplify the resulting equation. Combine like terms and reduce the equation as much as possible. If another radical remains, repeat the isolation and squaring process.
- Isolate the Second Radical:
If the equation still contains another radical, isolate this second radical. This may involve moving terms to the opposite side of the equation to facilitate further simplification.
- Square Again:
Square both sides of the equation again to eliminate the second radical. This should result in a polynomial equation, which can then be solved using standard algebraic methods.
- Check the Solution:
Always substitute your solutions back into the original equation to verify that they are valid. This is crucial as squaring both sides can introduce extraneous solutions that do not satisfy the original equation.
By following these steps diligently, you can solve radical equations with two radicals effectively. Practice with various examples to become more comfortable with the process, and always double-check your work to ensure accuracy.
Remember, the key to mastering radical equations is practice and understanding the underlying principles. Don't get discouraged by initial complexity; with perseverance, solving these equations will become second nature.
Hướng dẫn chi tiết về cách giải phương trình chứa căn với hai căn. Xem video để nắm rõ các bước và phương pháp hiệu quả.
Giải Phương Trình Chứa Căn (Căn Bậc Hai) Với Hai Căn
READ MORE:
Video hướng dẫn chi tiết về cách giải phương trình chứa hai căn. Hãy xem video để nắm rõ các bước và phương pháp hiệu quả.
Cách Giải Phương Trình Chứa Hai Căn