Topic how do you solve a radical expression: Welcome to our comprehensive guide on how do you solve a radical expression. In this article, we'll break down the process into simple, easy-to-follow steps, ensuring you gain a clear understanding of radical expressions and master the techniques needed to solve them efficiently. Let's dive in and simplify those radicals together!
Table of Content
- How to Solve Radical Equations
- Introduction to Radical Expressions
- Understanding Radicals
- Isolating the Radical
- Squaring Both Sides
- Simplifying and Solving
- Checking for Extraneous Solutions
- Example Problems
- Solving Equations with One Radical
- Solving Equations with Multiple Radicals
- Common Mistakes and How to Avoid Them
- Advanced Techniques for Complex Radicals
- Practice Problems and Solutions
- Resources for Further Learning
- YOUTUBE: Học cách đơn giản hóa biểu thức dưới dấu căn một cách dễ dàng với video hướng dẫn chi tiết và các ví dụ minh họa cụ thể.
How to Solve Radical Equations
Solving radical equations involves several key steps to ensure accurate solutions. Here, we outline the process and provide examples to illustrate each step.
Steps to Solve Radical Equations
- Isolate the radical expression on one side of the equation.
- Square both sides of the equation to eliminate the radical.
- Simplify and solve the resulting equation.
- Check all solutions in the original equation to identify any extraneous roots.
Example 1: Single Radical
Solve the equation \( \sqrt{2x + 9} - 5 = 0 \)
- Isolate the radical: \( \sqrt{2x + 9} = 5 \)
- Square both sides: \( ( \sqrt{2x + 9} )^2 = 5^2 \)
- Simplify: \( 2x + 9 = 25 \)
- Solve for \( x \):
- Subtract 9 from both sides: \( 2x = 16 \)
- Divide by 2: \( x = 8 \)
- Check the solution: \[ \sqrt{2(8) + 9} - 5 = \sqrt{16 + 9} - 5 = \sqrt{25} - 5 = 5 - 5 = 0 \] The solution \( x = 8 \) is correct.
Example 2: Multiple Radicals
Solve the equation \( \sqrt{2x - 5} - \sqrt{x - 1} = 1 \)
- Isolate one radical: \( \sqrt{2x - 5} = 1 + \sqrt{x - 1} \)
- Square both sides: \[ ( \sqrt{2x - 5} )^2 = (1 + \sqrt{x - 1})^2 \] Simplify: \( 2x - 5 = 1 + 2\sqrt{x - 1} + (x - 1) \)
- Isolate the remaining radical: \[ 2x - 5 - x - 1 = 2\sqrt{x - 1} \] Simplify: \( x - 6 = 2\sqrt{x - 1} \)
- Square both sides again: \[ (x - 6)^2 = (2\sqrt{x - 1})^2 \] Simplify: \( x^2 - 12x + 36 = 4(x - 1) \) \[ x^2 - 12x + 36 = 4x - 4 \] Combine like terms: \( x^2 - 16x + 40 = 0 \)
- Solve the quadratic equation: \[ x = \frac{16 \pm \sqrt{16^2 - 4 \cdot 1 \cdot 40}}{2 \cdot 1} = \frac{16 \pm \sqrt{256 - 160}}{2} = \frac{16 \pm \sqrt{96}}{2} = \frac{16 \pm 4\sqrt{6}}{2} \] Simplify: \( x = 8 \pm 2\sqrt{6} \)
- Check both solutions in the original equation to ensure they are valid.
Tips for Solving Radical Equations
- Always isolate the radical term first to simplify the equation.
- Remember to check for extraneous solutions, as squaring both sides can introduce invalid solutions.
- If the equation has more than one radical, isolate and eliminate them one at a time.
Conclusion
Solving radical equations involves careful manipulation of the equation to isolate radicals, followed by squaring to eliminate them, and finally verifying the solutions to ensure they are valid. By following the outlined steps, you can solve even complex radical equations accurately.

READ MORE:
Introduction to Radical Expressions
Radical expressions involve roots, such as square roots, cube roots, and so on. These expressions are fundamental in algebra and appear frequently in various mathematical problems. Understanding how to manipulate and solve radical expressions is crucial for progressing in math. Here's a detailed introduction to help you get started:
Definition: A radical expression contains a root symbol,
Basic Components:
- Radicand: The number or expression inside the root symbol.
- Index: The degree of the root. For example, in the cube root
\(\sqrt[3]{x}\) , the index is 3. - Radical Sign: The symbol
\(\sqrt{}\) indicating the root.
Steps to Simplify Radical Expressions:
- Identify Perfect Squares: Factor the radicand to find perfect square factors.
- Rewrite the Radical: Express the radicand as a product of its factors.
- Simplify: Take the square root of the perfect square factors and simplify the expression.
Example:
Simplify
- Factor 50 as
\(50 = 25 \times 2\) - Rewrite as
\(\sqrt{25 \times 2}\) - Simplify to
\(5\sqrt{2}\)
Understanding these basics is the first step in mastering radical expressions. With practice, you'll become more comfortable with more complex radicals and solving radical equations.
Understanding Radicals
Radicals, often represented by the radical symbol (√), are used to denote roots, such as square roots, cube roots, etc. A radical expression can be written in the form √a or ⁿ√a, where n is the index of the radical and a is the radicand.
Key Concepts
- Radicand: The number or expression inside the radical symbol.
- Index: The degree of the root. For square roots, the index is 2, and for cube roots, the index is 3.
- Perfect Squares and Cubes: Numbers like 4, 9, 16 (squares of 2, 3, 4 respectively) or 8, 27, 64 (cubes of 2, 3, 4 respectively).
Properties of Radicals
- The radical of a product:
√(ab) = √a * √b - The radical of a quotient:
√(a/b) = √a / √b - Power property:
(ⁿ√a)^m = a^(m/n)
Examples
Here are a few examples to illustrate the properties and simplification of radicals:
- Example 1:
√(16) = 4because 16 is a perfect square (4² = 16). - Example 2:
³√(27) = 3because 27 is a perfect cube (3³ = 27). - Example 3:
√(50) = √(25 * 2) = 5√2because 25 is a perfect square and can be factored out of the radical.
Simplifying Radicals
Simplifying radicals involves factoring the radicand into its prime factors and then applying the properties of radicals. Here are the steps:
- Factor the radicand: Break down the number inside the radical into its prime factors.
- Pair the factors: Group the prime factors into pairs.
- Move pairs outside: For every pair of factors, move one factor outside the radical.
- Combine remaining factors: Multiply any factors that remain inside the radical.
For example, to simplify √(72):
- Factor 72 into primes:
72 = 2 * 2 * 2 * 3 * 3 - Pair the factors:
(2 * 2) * (3 * 3) * 2 - Move pairs outside:
2 * 3 * √(2) - Result:
6√2
Conclusion
Understanding and simplifying radicals is an essential skill in algebra. By mastering the properties and techniques for working with radicals, you can solve a wide range of mathematical problems.
Isolating the Radical
To solve a radical equation, the first crucial step is to isolate the radical on one side of the equation. This makes it easier to eliminate the radical and solve the equation. Here are the detailed steps:
- Move the Radical: If there are any terms added or subtracted to the radical, move them to the other side of the equation using basic algebraic operations.
- Example: Let's start with the equation:
\[\sqrt{2x + 9} - 5 = 0\]
To isolate the radical, add 5 to both sides:
\[\sqrt{2x + 9} = 5\] - Divide if Necessary: If the radical is multiplied by a coefficient, divide both sides by that coefficient to isolate the radical term.
- Example: Consider:
\[3\sqrt{3x - 5} = 12\]
Divide both sides by 3:
\[\sqrt{3x - 5} = 4\] - Double-check: Ensure that the radical term is completely isolated on one side of the equation before proceeding to the next steps of squaring both sides.
By following these steps, you can successfully isolate the radical term, making it easier to solve the equation.
Squaring Both Sides
Squaring both sides of a radical equation is a crucial step in solving it. This method helps to eliminate the radical, allowing you to work with a polynomial equation. Here's a detailed, step-by-step guide on how to do this:
-
Isolate the Radical: Ensure the radical expression is alone on one side of the equation.
Example: \( \sqrt{2x + 3} = 5 \)
-
Square Both Sides: Apply the squaring operation to both sides of the equation to eliminate the radical.
Example: \( (\sqrt{2x + 3})^2 = 5^2 \)
Result: \( 2x + 3 = 25 \)
-
Simplify and Solve: Solve the resulting polynomial equation for the variable.
Example: \( 2x + 3 = 25 \)
Simplify: \( 2x = 22 \)
Solve: \( x = 11 \)
-
Check for Extraneous Solutions: Substitute the solution back into the original equation to verify its validity. Squaring both sides can sometimes introduce extraneous solutions that don't satisfy the original equation.
Example: Substitute \( x = 11 \) back into \( \sqrt{2x + 3} = 5 \)
Check: \( \sqrt{2(11) + 3} = \sqrt{25} = 5 \)
Since \( 5 = 5 \), the solution \( x = 11 \) is valid.
By following these steps, you can effectively eliminate the radical and solve the equation. It's important to always check your solutions to ensure they are not extraneous, as this is a common issue when squaring both sides of an equation.

Simplifying and Solving
Once the radical is isolated and both sides have been squared, the next step is to simplify and solve the resulting equation. Here are the steps to follow:
- Simplify the equation obtained after squaring both sides:
- Combine like terms.
- Move all terms to one side to set the equation to zero, if needed.
- Solve the simplified equation:
- Use algebraic methods such as factoring, the quadratic formula, or other appropriate techniques.
- Check for extraneous solutions:
- Substitute the solutions back into the original radical equation to verify that they work.
Let's go through an example:
Example: Solve the equation \(\sqrt{3x - 5} + 2 = 7\)
- Isolate the radical:
- \(\sqrt{3x - 5} = 7 - 2\)
- \(\sqrt{3x - 5} = 5\)
- Square both sides:
- \((\sqrt{3x - 5})^2 = 5^2\)
- \(3x - 5 = 25\)
- Simplify the equation:
- Move the constant to the other side: \(3x - 5 + 5 = 25 + 5\)
- \(3x = 30\)
- Divide by 3: \(x = 10\)
- Check the solution:
- Substitute \(x = 10\) back into the original equation:
- \(\sqrt{3(10) - 5} + 2 = 7\)
- \(\sqrt{30 - 5} + 2 = 7\)
- \(\sqrt{25} + 2 = 7\)
- \(5 + 2 = 7\)
- Since the left side equals the right side, \(x = 10\) is a valid solution.
Checking for Extraneous Solutions
When solving radical equations, it is crucial to check for extraneous solutions. These are solutions that appear valid through algebraic manipulation but do not satisfy the original equation. Here are the steps to check for extraneous solutions:
- Solve the Equation: Follow the standard steps to solve the radical equation. This involves isolating the radical, squaring both sides, and solving the resulting equation.
- Substitute the Solutions: Once you have potential solutions, substitute each one back into the original equation to verify if it holds true.
- Check Each Solution: Evaluate the left and right sides of the original equation separately using each potential solution. If both sides are equal, the solution is valid. If not, it is an extraneous solution.
Let's consider an example:
Solve the equation: \( \sqrt{2x + 3} = x - 1 \)
- Step 1: Square both sides of the equation to eliminate the radical:
\( (\sqrt{2x + 3})^2 = (x - 1)^2 \) \( 2x + 3 = x^2 - 2x + 1 \) - Step 2: Rearrange the equation to set it to zero:
\( x^2 - 4x - 2 = 0 \) - Step 3: Solve the quadratic equation:
Using the quadratic formula: \( x = \frac{4 \pm \sqrt{16 + 8}}{2} \) \( x = \frac{4 \pm \sqrt{24}}{2} \) \( x = \frac{4 \pm 2\sqrt{6}}{2} \) \( x = 2 \pm \sqrt{6} \) - Step 4: Check each solution:
For \( x = 2 + \sqrt{6} \): \( \sqrt{2(2 + \sqrt{6}) + 3} = 2 + \sqrt{6} - 1 \) \( \sqrt{4 + 2\sqrt{6} + 3} = 1 + \sqrt{6} \) \( \sqrt{7 + 2\sqrt{6}} \neq 1 + \sqrt{6} \) Thus, \( x = 2 + \sqrt{6} \) is extraneous. For \( x = 2 - \sqrt{6} \): \( \sqrt{2(2 - \sqrt{6}) + 3} = 2 - \sqrt{6} - 1 \) \( \sqrt{4 - 2\sqrt{6} + 3} = 1 - \sqrt{6} \) \( \sqrt{7 - 2\sqrt{6}} = 1 - \sqrt{6} \) Thus, \( x = 2 - \sqrt{6} \) is valid.
Therefore, the only valid solution is \( x = 2 - \sqrt{6} \). Checking for extraneous solutions ensures that the solutions satisfy the original radical equation and eliminates any incorrect results introduced during the solving process.
Example Problems
Here are some example problems to help you understand how to solve radical equations. Each problem is solved step-by-step to illustrate the process.
Example 1: Solving a Simple Radical Equation
Solve the equation \( \sqrt{2x + 9} - 5 = 0 \).
- Isolate the radical on one side of the equation:
\( \sqrt{2x + 9} = 5 \)
- Square both sides to eliminate the radical:
\( (\sqrt{2x + 9})^2 = 5^2 \)
\( 2x + 9 = 25 \)
- Solve the resulting equation:
\( 2x = 25 - 9 \)
\( 2x = 16 \)
\( x = \frac{16}{2} \)
\( x = 8 \)
- Check the solution by substituting it back into the original equation:
\( \sqrt{2(8) + 9} - 5 = \sqrt{25} - 5 = 5 - 5 = 0 \)
The solution \( x = 8 \) is correct.
Example 2: Solving an Equation with Two Radicals
Solve the equation \( \sqrt{2x - 5} - \sqrt{x - 1} = 1 \).
- Isolate one of the radicals:
\( \sqrt{2x - 5} = 1 + \sqrt{x - 1} \)
- Square both sides to eliminate the first radical:
\( (\sqrt{2x - 5})^2 = (1 + \sqrt{x - 1})^2 \)
\( 2x - 5 = 1 + 2\sqrt{x - 1} + (x - 1) \)
\( 2x - 5 = x + 1 + 2\sqrt{x - 1} \)
- Isolate the remaining radical:
\( 2x - 5 - x - 1 = 2\sqrt{x - 1} \)
\( x - 6 = 2\sqrt{x - 1} \)
- Square both sides again:
\( (x - 6)^2 = (2\sqrt{x - 1})^2 \)
\( x^2 - 12x + 36 = 4(x - 1) \)
\( x^2 - 12x + 36 = 4x - 4 \)
\( x^2 - 16x + 40 = 0 \)
- Solve the quadratic equation:
\( x = \frac{16 \pm \sqrt{256 - 160}}{2} \)
\( x = \frac{16 \pm \sqrt{96}}{2} \)
\( x = \frac{16 \pm 4\sqrt{6}}{2} \)
\( x = 8 \pm 2\sqrt{6} \)
- Check the solutions to ensure they are not extraneous:
- For \( x = 8 + 2\sqrt{6} \):
\( \sqrt{2(8 + 2\sqrt{6}) - 5} - \sqrt{8 + 2\sqrt{6} - 1} = 1 \)
Check to see if it holds true.
- For \( x = 8 - 2\sqrt{6} \):
\( \sqrt{2(8 - 2\sqrt{6}) - 5} - \sqrt{8 - 2\sqrt{6} - 1} = 1 \)
Check to see if it holds true.
- For \( x = 8 + 2\sqrt{6} \):
Example 3: Solving an Equation with a Cube Root
Solve the equation \( \sqrt[3]{4x - 3} = \sqrt[3]{3x + 2} \).
- Since the radicals are already isolated, cube both sides:
\( (\sqrt[3]{4x - 3})^3 = (\sqrt[3]{3x + 2})^3 \)
\( 4x - 3 = 3x + 2 \)
- Solve the resulting equation:
\( 4x - 3 = 3x + 2 \)
\( x = 5 \)
- Check the solution by substituting it back into the original equation:
\( \sqrt[3]{4(5) - 3} = \sqrt[3]{3(5) + 2} \)
\( \sqrt[3]{20 - 3} = \sqrt[3]{15 + 2} \)
\( \sqrt[3]{17} = \sqrt[3]{17} \)
The solution \( x = 5 \) is correct.
Solving Equations with One Radical
Solving equations with one radical involves isolating the radical on one side of the equation, squaring both sides to eliminate the radical, and then solving the resulting equation. Here are the detailed steps:
-
Isolate the Radical:
Move all other terms to the opposite side of the equation to isolate the radical expression.
Example:
\[\sqrt{2x + 3} - 1 = 0 \]
To isolate the radical, add 1 to both sides:
\[\sqrt{2x + 3} = 1 \]
-
Square Both Sides:
Square both sides of the equation to eliminate the square root.
Example:
\[\left(\sqrt{2x + 3}\right)^2 = 1^2 \]
Which simplifies to:
\[2x + 3 = 1 \]
-
Simplify and Solve:
Solve the resulting equation as you would any linear equation.
Example:
Subtract 3 from both sides:
\[2x = -2 \]
Divide by 2:
\[x = -1 \]
-
Check for Extraneous Solutions:
Substitute the solution back into the original equation to ensure it is valid, as squaring both sides can introduce extraneous solutions.
Example:
Substitute \( x = -1 \) back into the original equation:
\[\sqrt{2(-1) + 3} - 1 = 0 \]
\[\sqrt{-2 + 3} - 1 = 0 \]
\[\sqrt{1} - 1 = 0 \]
\[1 - 1 = 0 \]
The solution \( x = -1 \) is valid.
By following these steps, you can solve any equation that contains a single radical. Always remember to verify your solutions to avoid extraneous roots.

Solving Equations with Multiple Radicals
When solving equations with multiple radicals, the process can be more complex but follows similar steps to solving single radical equations. The key is to isolate each radical term one at a time and eliminate them through repeated squaring. Here’s a detailed step-by-step method:
-
Isolate One Radical: Choose one of the radicals to isolate on one side of the equation. If possible, isolate the more complicated radical first.
Example: Solve \( \sqrt{2x-5} - \sqrt{x-1} = 1 \)
- Isolate one radical: \( \sqrt{2x-5} = 1 + \sqrt{x-1} \)
-
Square Both Sides: Square both sides of the equation to eliminate the isolated radical.
- Square both sides: \( (\sqrt{2x-5})^2 = (1 + \sqrt{x-1})^2 \)
- Simplify: \( 2x-5 = 1 + 2\sqrt{x-1} + (x-1) \)
- Combine like terms: \( 2x-5 = x + 2\sqrt{x-1} \)
-
Isolate the Remaining Radical: If another radical term remains, isolate it on one side of the equation.
- Isolate the remaining radical: \( x-5 = 2\sqrt{x-1} \)
-
Square Both Sides Again: Square both sides again to eliminate the second radical.
- Square both sides: \( (x-5)^2 = (2\sqrt{x-1})^2 \)
- Simplify: \( x^2 - 10x + 25 = 4(x-1) \)
- Combine like terms: \( x^2 - 10x + 25 = 4x - 4 \)
- Rearrange to form a quadratic equation: \( x^2 - 14x + 29 = 0 \)
-
Solve the Quadratic Equation: Use the quadratic formula \( x = \frac{-b \pm \sqrt{b^2-4ac}}{2a} \) to find the values of \( x \).
- For \( x^2 - 14x + 29 = 0 \), solve using \( a = 1 \), \( b = -14 \), and \( c = 29 \).
-
Check for Extraneous Solutions: Substitute the solutions back into the original equation to verify that they satisfy the equation. Extraneous solutions may arise from the squaring steps.
- Example check: If one solution is \( x = 11.47 \), substitute back: \( \sqrt{2(11.47)-5} - \sqrt{11.47-1} = 1 \).
By following these steps methodically, you can solve equations with multiple radicals. Always remember to check for extraneous solutions at the end to ensure the validity of your answers.
Common Mistakes and How to Avoid Them
When solving radical expressions, students often make several common mistakes. Understanding these errors can help avoid them and ensure accurate solutions. Below are some frequent mistakes and tips on how to prevent them:
-
Incorrectly Squaring Terms Instead of Sides:
Always square both sides of the equation, not the individual terms. For example:
\[
\text{If } \sqrt{x+3} = 4, \text{ then square both sides: } (\sqrt{x+3})^2 = 4^2 \Rightarrow x + 3 = 16.
\]Avoid squaring terms separately, which can lead to incorrect results.
-
Forgetting to Check for Extraneous Solutions:
Squaring both sides of an equation can introduce extraneous solutions. Always substitute your solutions back into the original equation to verify their validity. For example:
\[
\text{If } x = 2 \text{ is a solution for } \sqrt{x+5} - x = 0, \text{ check: } \sqrt{2+5} - 2 = \sqrt{7} - 2 \neq 0.
\]Here, \( x = 2 \) is not a valid solution.
-
Mishandling Negative Signs:
When dealing with square roots, remember that they represent only the principal (non-negative) square root. For example:
\[
\sqrt{x^2} = |x|, \text{ not simply } x.
\]Ensure you consider both positive and negative roots where applicable.
-
Assuming All Functions Are Linear:
Radical expressions do not follow the properties of linear functions. Avoid assuming additivity and homogeneity for non-linear functions:
\[
(x+y)^2 \neq x^2 + y^2 \text{ and } \sqrt{x+y} \neq \sqrt{x} + \sqrt{y}.Use the correct operations for radicals to avoid mistakes.
-
Misapplying the Equals Sign:
Always balance both sides of an equation. Manipulating expressions improperly can lead to incorrect conclusions:
\[
\text{For } \sqrt{x} = -3, \text{ squaring both sides yields } x = 9, \text{ but this should be checked back in the original equation, which yields no solution as } \sqrt{x} \text{ cannot be negative}.
By being aware of these common pitfalls and practicing careful problem-solving techniques, you can improve your accuracy in solving radical expressions.
Advanced Techniques for Complex Radicals
Solving equations involving complex radicals often requires advanced techniques beyond simple isolation and squaring. Here are several methods to tackle these problems effectively:
1. Rationalizing the Denominator
Rationalizing the denominator involves eliminating radicals from the denominator of a fraction. For example, to rationalize \( \frac{1}{\sqrt{a}} \), multiply the numerator and denominator by \( \sqrt{a} \):
\[
\frac{1}{\sqrt{a}} \times \frac{\sqrt{a}}{\sqrt{a}} = \frac{\sqrt{a}}{a}
\]
2. Solving Equations with Rational Exponents
Equations with rational exponents can be solved by raising both sides to the reciprocal of the exponent. For example, solve \( x^{\frac{3}{2}} = 27 \):
\[
(x^{\frac{3}{2}})^{\frac{2}{3}} = 27^{\frac{2}{3}} \implies x = 9
\]
3. Isolating and Eliminating Radicals
When an equation has multiple radicals, isolate one radical at a time and eliminate them through squaring. Consider the equation \( \sqrt{2x + 3} + \sqrt{x - 2} = 4 \):
- Isolate one radical:
\[
\sqrt{2x + 3} = 4 - \sqrt{x - 2}
\] - Square both sides:
\[
(\sqrt{2x + 3})^2 = (4 - \sqrt{x - 2})^2 \implies 2x + 3 = 16 - 8\sqrt{x - 2} + x - 2
\] - Combine like terms and isolate the second radical:
\[
x + 1 = -8\sqrt{x - 2} \implies \sqrt{x - 2} = -\frac{x + 1}{8}
\] - Square both sides again:
\[
(x - 2) = \left( -\frac{x + 1}{8} \right)^2
\] - Solve the resulting equation.
4. Using the Conjugate
To simplify expressions with radicals, multiply by the conjugate. For instance, simplify \( \frac{1}{\sqrt{a} + \sqrt{b}} \) by multiplying the numerator and denominator by the conjugate \( \sqrt{a} - \sqrt{b} \):
\[
\frac{1}{\sqrt{a} + \sqrt{b}} \times \frac{\sqrt{a} - \sqrt{b}}{\sqrt{a} - \sqrt{b}} = \frac{\sqrt{a} - \sqrt{b}}{a - b}
\]
5. Factoring and Rational Exponents
Solving equations that involve rational exponents often requires factoring. For example, to solve \( 3x^{\frac{3}{4}} = x^{\frac{1}{2}} \):
- Rewrite with a common base:
\[
3x^{\frac{3}{4}} - x^{\frac{2}{4}} = 0
\] - Factor out the smallest exponent:
\[
x^{\frac{1}{2}}(3x^{\frac{1}{4}} - 1) = 0
\] - Solve for \( x \):
\[
x^{\frac{1}{2}} = 0 \quad \text{or} \quad 3x^{\frac{1}{4}} = 1 \implies x = \left(\frac{1}{3}\right)^4
\]
6. Verification of Solutions
Always verify your solutions by substituting them back into the original equation to check for extraneous solutions. This step ensures that all solutions are valid and satisfy the original problem.
Practice Problems and Solutions
Practice problems are essential to mastering the techniques required to solve radical equations. Below are several practice problems along with detailed solutions to help you understand the process step-by-step.
Problem 1
Solve the radical equation:
$$ \sqrt{5x + 11} - 1 = x $$
- Isolate the radical on one side of the equation:
$$ \sqrt{5x + 11} = x + 1 $$
- Square both sides to eliminate the radical:
$$ (\sqrt{5x + 11})^2 = (x + 1)^2 $$
$$ 5x + 11 = x^2 + 2x + 1 $$
- Rearrange the equation to set it to zero:
$$ x^2 - 3x - 10 = 0 $$
- Factorize and solve for \( x \):
$$ (x - 5)(x + 2) = 0 $$
Possible solutions: \( x = 5 \) or \( x = -2 \)
- Check both solutions in the original equation to identify extraneous solutions:
For \( x = 5 \):
$$ \sqrt{5(5) + 11} - 1 = 5 $$
$$ \sqrt{36} - 1 = 5 $$
$$ 6 - 1 = 5 \, \text{(True)} $$
For \( x = -2 \):
$$ \sqrt{5(-2) + 11} - 1 = -2 $$
$$ \sqrt{1} - 1 = -2 $$
$$ 1 - 1 = -2 \, \text{(False)} $$
Therefore, the only solution is \( x = 5 \).
Problem 2
Solve the radical equation:
$$ \sqrt{x - 4} - \sqrt{x} = -2 $$
- Isolate one of the radicals:
$$ \sqrt{x - 4} = \sqrt{x} - 2 $$
- Square both sides to eliminate the radicals:
$$ ( \sqrt{x - 4} )^2 = ( \sqrt{x} - 2 )^2 $$
$$ x - 4 = x - 4\sqrt{x} + 4 $$
- Isolate the remaining radical:
$$ -8 = -4\sqrt{x} $$
$$ 2 = \sqrt{x} $$
- Square both sides again:
$$ 4 = x $$
- Check the solution in the original equation:
$$ \sqrt{4 - 4} - \sqrt{4} = -2 $$
$$ 0 - 2 = -2 \, \text{(True)} $$
Therefore, the solution is \( x = 4 \).
Problem 3
Solve the radical equation:
$$ \sqrt{x + 6} + 2 = x $$
- Isolate the radical:
$$ \sqrt{x + 6} = x - 2 $$
- Square both sides:
$$ ( \sqrt{x + 6} )^2 = ( x - 2 )^2 $$
$$ x + 6 = x^2 - 4x + 4 $$
- Rearrange the equation to set it to zero:
$$ x^2 - 5x - 2 = 0 $$
- Use the quadratic formula to solve for \( x \):
$$ x = \frac{5 \pm \sqrt{25 + 8}}{2} $$
$$ x = \frac{5 \pm \sqrt{33}}{2} $$
- Check both solutions in the original equation to identify extraneous solutions:
Substitute \( x \approx 5.37 \) and \( x \approx -0.37 \) back into the original equation to verify which, if any, are valid.
Problem 4
Solve the radical equation:
$$ \sqrt{3x - 11} = 3x - x $$
- Isolate the radical:
$$ \sqrt{3x - 11} = 2x $$
- Square both sides:
$$ ( \sqrt{3x - 11} )^2 = ( 2x )^2 $$
$$ 3x - 11 = 4x^2 $$
- Rearrange the equation to set it to zero:
$$ 4x^2 - 3x + 11 = 0 $$
- Use the quadratic formula to solve for \( x \):
$$ x = \frac{3 \pm \sqrt{(-3)^2 - 4 \cdot 4 \cdot 11}}{2 \cdot 4} $$
$$ x = \frac{3 \pm \sqrt{9 - 176}}{8} $$
$$ x = \frac{3 \pm \sqrt{-167}}{8} $$
Since the discriminant is negative, there are no real solutions.
These practice problems cover a range of scenarios and demonstrate the steps required to solve radical equations effectively. Practice these problems and check your solutions thoroughly to ensure understanding and accuracy.
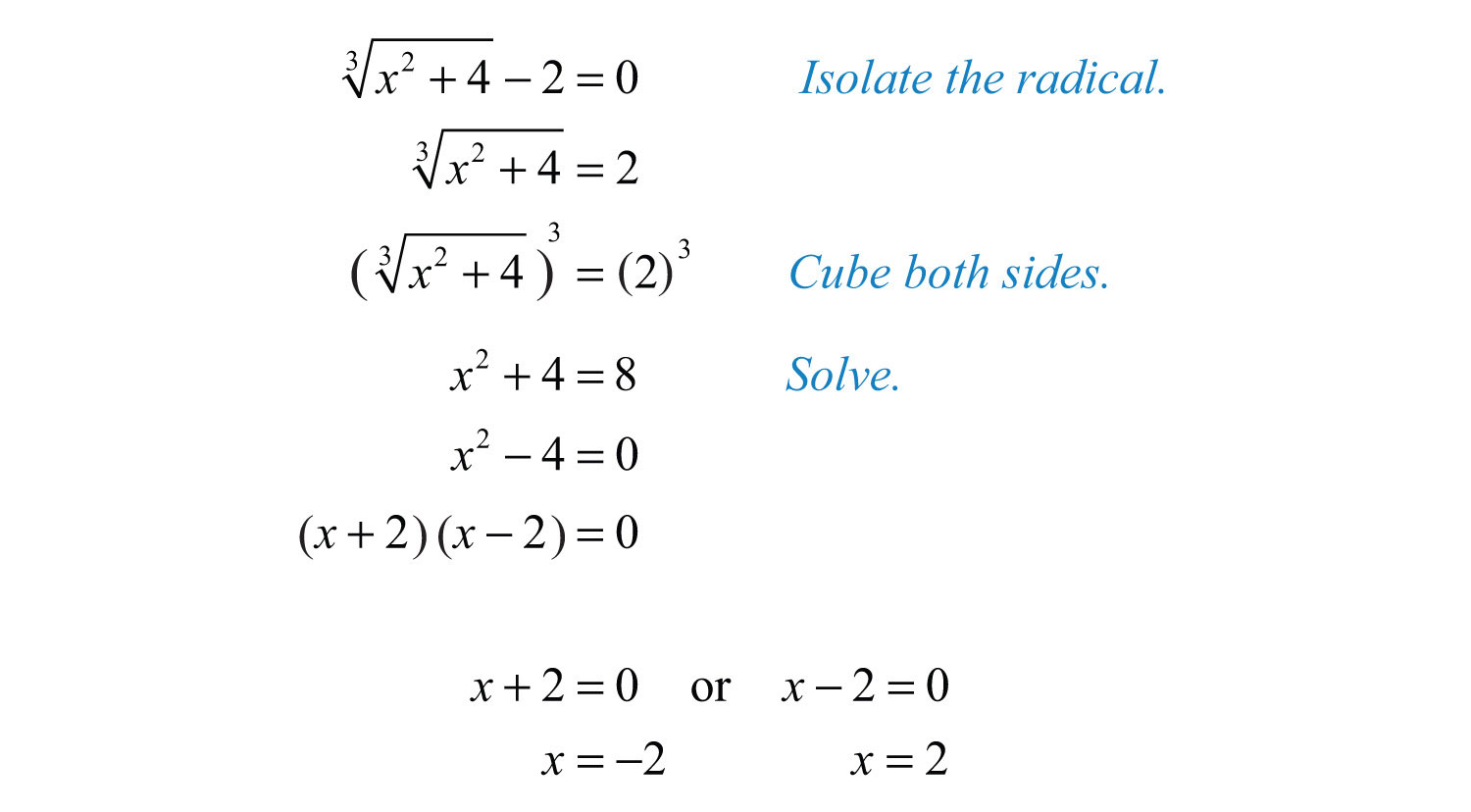
Resources for Further Learning
Understanding and solving radical expressions and equations can be challenging, but with the right resources, you can master these concepts. Here are some valuable resources to help you further your learning:
-
Online Tutorials and Courses
-
: Offers comprehensive tutorials on solving radical equations, complete with video lessons and practice exercises.
-
: Provides a variety of algebra courses from top universities and institutions that include modules on radicals and their applications.
-
-
Textbooks and eBooks
-
: A widely-used textbook that covers a broad range of algebra topics, including radical expressions and equations.
-
: A free, open-source textbook that includes detailed explanations and examples on radicals.
-
-
Practice and Problem-Solving Platforms
-
: Offers a vast array of practice problems tailored to help students improve their skills in solving radical expressions and equations.
-
: A useful tool for solving a variety of math problems, including those involving radicals. It also provides step-by-step solutions.
-
-
Video Lectures and Demonstrations
-
: Features detailed video lectures on algebraic topics, including step-by-step guides to solving radical equations.
-
: Offers concise and clear explanations on a wide range of math topics, including radicals.
-
-
Interactive Tools and Apps
-
: An incredibly powerful computational tool that can help you solve complex radical equations and provide detailed explanations.
-
: A mobile app that allows you to scan math problems and see step-by-step solutions. It's especially useful for checking your work on radical equations.
-
By leveraging these resources, you can gain a deeper understanding of radical expressions and equations, practice your skills, and enhance your problem-solving abilities. Happy learning!
Học cách đơn giản hóa biểu thức dưới dấu căn một cách dễ dàng với video hướng dẫn chi tiết và các ví dụ minh họa cụ thể.
Đơn Giản Hóa Biểu Thức Dưới Dấu Căn - Phương Pháp Dễ Dàng
READ MORE:
Khám phá cách đơn giản hóa biểu thức dưới dấu căn có biến số qua video hướng dẫn chi tiết, dễ hiểu và các ví dụ minh họa cụ thể.
Đơn Giản Hóa Biểu Thức Dưới Dấu Căn Với Biến Số