Topic how to simplify a square root with variables: Learning how to simplify a square root with variables is an essential skill in algebra. This guide provides clear steps and practical tips to master this process effortlessly. Whether you're dealing with single or multiple variables, you'll find straightforward explanations and examples to help you simplify square roots with confidence.
Table of Content
- Simplifying Square Roots with Variables
- Introduction to Simplifying Square Roots with Variables
- Basic Concepts and Terminology
- Step-by-Step Process for Simplifying
- Identifying Perfect Squares
- Prime Factorization
- Simplifying Square Roots with Single Variables
- Simplifying Square Roots with Multiple Variables
- Examples and Practice Problems
- Special Cases and Common Mistakes
- Application in Algebraic Expressions
- FAQs and Troubleshooting Tips
- Additional Resources and References
- YOUTUBE: Video hướng dẫn đơn giản hóa căn bậc hai với biến số, giúp người xem hiểu rõ và nắm vững kiến thức về chủ đề này.
Simplifying Square Roots with Variables
When simplifying square roots that contain variables, the goal is to factor the expression inside the radical to find perfect squares. These can then be simplified by taking their square roots. Here are the steps and examples to illustrate the process:
Steps to Simplify Square Roots with Variables
- Factor the Expression: Break down the number and variables inside the square root into their prime factors or simplest components.
- Identify Perfect Squares: Look for pairs of identical factors, as these will be perfect squares.
- Separate the Factors: Rewrite the expression so that perfect squares are grouped together.
- Simplify: Take the square root of each perfect square factor, simplifying the expression.
Example 1: Simplify \( \sqrt{9x^6} \)
Factor the expression inside the square root:
\( \sqrt{9x^6} = \sqrt{3^2 \cdot (x^3)^2} \)
Separate the perfect squares:
\( \sqrt{3^2} \cdot \sqrt{(x^3)^2} \)
Take the square root of each factor:
\( 3 \cdot |x^3| \)
Answer: \( \sqrt{9x^6} = 3|x^3| \)
Example 2: Simplify \( \sqrt{100x^2y^4} \)
Factor the expression inside the square root:
\( \sqrt{100x^2y^4} = \sqrt{10^2 \cdot x^2 \cdot (y^2)^2} \)
Separate the perfect squares:
\( \sqrt{10^2} \cdot \sqrt{x^2} \cdot \sqrt{(y^2)^2} \)
Take the square root of each factor:
\( 10 \cdot |x| \cdot y^2 \)
Answer: \( \sqrt{100x^2y^4} = 10|x|y^2 \)
Example 3: Simplify \( \sqrt{49x^{10}y^8} \)
Factor the expression inside the square root:
\( \sqrt{49x^{10}y^8} = \sqrt{7^2 \cdot (x^5)^2 \cdot (y^4)^2} \)
Separate the perfect squares:
\( \sqrt{7^2} \cdot \sqrt{(x^5)^2} \cdot \sqrt{(y^4)^2} \)
Take the square root of each factor:
\( 7 \cdot |x^5| \cdot y^4 \)
Answer: \( \sqrt{49x^{10}y^8} = 7|x^5|y^4 \)

READ MORE:
Introduction to Simplifying Square Roots with Variables
Simplifying square roots with variables involves breaking down complex radical expressions into simpler forms. This process requires understanding both numerical and variable factors within the radical. Here, we present a step-by-step guide to help you master this essential algebraic skill.
To start, consider the expression \( \sqrt{a \cdot b} \). This can be separated into \( \sqrt{a} \cdot \sqrt{b} \). Applying this to variables, for example, \( \sqrt{x^4} \), we rewrite it as \( \sqrt{(x^2)^2} = x^2 \).
Here are the key steps:
- Identify Perfect Squares: Look for perfect square factors within the radicand. For example, in \( \sqrt{18x^4} \), \( 18 \) can be factored into \( 9 \cdot 2 \) where \( 9 \) is a perfect square.
- Separate Factors: Rewrite the radicand as a product of perfect squares and other factors. Using the previous example, \( \sqrt{18x^4} \) becomes \( \sqrt{9 \cdot 2 \cdot (x^2)^2} \).
- Simplify Each Part: Take the square root of the perfect squares separately. This gives us \( \sqrt{9} \cdot \sqrt{2} \cdot \sqrt{(x^2)^2} = 3 \cdot \sqrt{2} \cdot x^2 \).
- Combine Results: Combine the simplified parts to get the final simplified expression. In this case, \( 3x^2\sqrt{2} \).
Let’s apply these steps to more complex expressions:
| Expression | Steps | Simplified Form |
| \( \sqrt{50x^6} \) |
|
\( 5x^3\sqrt{2} \) |
| \( \sqrt{72y^8} \) |
|
\( 6y^4\sqrt{2} \) |
With these steps, you can confidently simplify square roots with variables, making complex expressions more manageable and easier to work with in algebraic operations.
Basic Concepts and Terminology
Understanding how to simplify square roots with variables starts with a grasp of fundamental concepts and terminology. This section will cover essential ideas and definitions that will form the basis for simplifying these expressions.
- Radical: An expression that includes a root, such as a square root or cube root. For example, \( \sqrt{x} \) or \( \sqrt[3]{x} \).
- Radicand: The number or expression inside the radical sign. In \( \sqrt{x^2y} \), \( x^2y \) is the radicand.
- Index: The small number outside and to the left of the radical sign that indicates the degree of the root. In \( \sqrt[3]{x} \), 3 is the index.
- Perfect Square: A number that is the square of an integer. For example, 1, 4, 9, 16, etc.
Let's delve deeper into these concepts with some examples.
- Identifying Perfect Squares: Recognizing perfect squares is crucial. For instance, \( x^2 \) and \( y^4 \) are perfect squares because \( x \) and \( y^2 \) are squared respectively.
- Simplifying Radicals: To simplify a square root with variables, we look for pairs of identical factors under the radical. For example, \( \sqrt{x^2} = x \) and \( \sqrt{y^4} = y^2 \).
- Absolute Values: When simplifying, we sometimes use absolute values to ensure non-negative results. For instance, \( \sqrt{x^2} = |x| \).
Here are step-by-step instructions for simplifying a square root with variables:
- Factor the radicand into prime factors, including variables.
- Group identical pairs of factors.
- Move each pair of factors outside the radical.
- Simplify the expression, ensuring to use absolute values if necessary.
Let's work through an example:
Simplify \( \sqrt{12x^5y^4} \):
- Factor the radicand: \( 12 = 2^2 \cdot 3 \), so \( 12x^5y^4 = 2^2 \cdot 3 \cdot x^4 \cdot x \cdot y^4 \).
- Group pairs: \( \sqrt{(2^2) \cdot 3 \cdot (x^4) \cdot x \cdot (y^4)} \).
- Simplify pairs: \( 2x^2y^2 \sqrt{3x} \).
The simplified form is \( 2x^2y^2 \sqrt{3x} \).
By understanding and applying these basic concepts and steps, you can simplify square roots with variables effectively.
Step-by-Step Process for Simplifying
To simplify a square root with variables, follow these steps:
- Identify and separate the coefficients and variable parts under the square root.
- Factorize the coefficients into prime factors and rewrite the variables with even exponents as squares.
- Separate the factors inside the square root into individual square roots.
- Simplify each square root by taking the square root of the perfect squares.
- Combine the simplified parts to get the final answer.
Let's apply this step-by-step process with an example:
Example: Simplify \( \sqrt{50x^8y^5} \).
- Factorize the coefficient and rewrite the variables: \( \sqrt{50 \cdot x^8 \cdot y^5} = \sqrt{2 \cdot 5^2 \cdot (x^4)^2 \cdot y^4 \cdot y} \).
- Separate the factors: \( \sqrt{2} \cdot \sqrt{5^2} \cdot \sqrt{(x^4)^2} \cdot \sqrt{y^4} \cdot \sqrt{y} \).
- Simplify each square root: \( \sqrt{2} \cdot 5 \cdot x^4 \cdot y^2 \cdot \sqrt{y} \).
- Combine the simplified parts: \( 5x^4y^2\sqrt{2y} \).
Therefore, \( \sqrt{50x^8y^5} = 5x^4y^2\sqrt{2y} \).
Identifying Perfect Squares
Identifying perfect squares is a crucial step in simplifying square roots, especially when variables are involved. A perfect square is a number or expression that can be written as the square of another number or expression. For example, 1, 4, 9, 16, and 25 are perfect squares because they can be written as \(1^2\), \(2^2\), \(3^2\), \(4^2\), and \(5^2\) respectively.
When dealing with variables, a variable term is a perfect square if its exponent is even. Here is a step-by-step guide to identifying perfect squares:
- List of Perfect Squares: Memorize the first few perfect squares to quickly identify them. The list includes numbers like 1, 4, 9, 16, 25, and so on.
- Perfect Square Variables: A variable with an even exponent is a perfect square. For example, \(x^2\), \(y^4\), and \(z^6\) are all perfect squares. The square root of \(x^8\) is \(x^4\).
- Combining Terms: A product of perfect squares is also a perfect square. For example, \(4x^2\) is a perfect square because both 4 and \(x^2\) are perfect squares.
Here is a quick reference table for perfect squares:
| 1 | 12 |
| 4 | 22 |
| 9 | 32 |
| 16 | 42 |
| 25 | 52 |
| 36 | 62 |
| 49 | 72 |
| 64 | 82 |
| 81 | 92 |
| 100 | 102 |
For variables, remember the key rule: the exponent must be even for the variable to be a perfect square. For example, \(x^{12}\) is a perfect square because the exponent 12 is even. Its square root is \(x^6\).

Prime Factorization
Prime factorization is a crucial step in simplifying square roots with variables. It involves breaking down the number and variables inside the square root into their prime factors. Here’s a detailed, step-by-step guide:
-
Identify Prime Factors: Break down the coefficients and variables inside the square root into their prime factors. For example, for the expression \( \sqrt{72x^6} \), factor 72 as \( 2^3 \times 3^2 \) and recognize that \( x^6 \) is already in its prime form.
-
Group Pairs of Factors: According to the property of square roots, \( \sqrt{a^2} = a \). Group the factors into pairs. For \( \sqrt{72x^6} \), we get \( \sqrt{(2^2 \times 2) \times (3^2) \times (x^6)} \).
-
Extract Pairs Out of the Square Root: Each pair of identical factors can be taken out of the square root. In our example, \( 2^2 \) and \( 3^2 \) can be taken out as 2 and 3 respectively, and \( x^6 \) can be taken out as \( x^3 \). Thus, \( \sqrt{72x^6} = 2 \times 3 \times x^3 \times \sqrt{2} = 6x^3\sqrt{2} \).
-
Simplify the Expression: Combine the extracted factors. For the above example, the simplified form is \( 6x^3\sqrt{2} \).
Using these steps ensures that square roots with variables are simplified correctly and efficiently.
Simplifying Square Roots with Single Variables
To simplify square roots with single variables, follow these steps:
- Identify the variable and its exponent inside the square root. For example, consider \( \sqrt{x^6} \).
- Factor the exponent into pairs: \( x^6 = x^3 \cdot x^3 \).
- Rewrite the expression to show the pairs as squares: \( \sqrt{x^3 \cdot x^3} = \sqrt{(x^3)^2} \).
- Take the square root of the squared term: \( \sqrt{(x^3)^2} = |x^3| \). Note that absolute value is used to ensure the result is non-negative.
Let's consider a detailed example:
- Simplify \( \sqrt{25x^4} \).
- Identify and separate the factors: \( \sqrt{25 \cdot x^4} = \sqrt{25} \cdot \sqrt{x^4} \).
- Simplify each square root: \( \sqrt{25} = 5 \) and \( \sqrt{x^4} = x^2 \).
- Combine the results: \( 5x^2 \).
This method can be applied to any variable with an even exponent inside the square root, making it straightforward to simplify such expressions effectively.
Simplifying Square Roots with Multiple Variables
When simplifying square roots involving multiple variables, the process involves breaking down each component into its simplest form. Here are the detailed steps:
- Factorize each term inside the square root to identify perfect squares.
- Rewrite the square root expression by separating the perfect squares from the non-perfect squares.
- Simplify the square root of the perfect squares.
- Combine the simplified terms to form the final expression.
Let's look at an example:
Simplify the expression \( \sqrt{12x^5y^2} \).
- Factorize \( 12 \) into \( 2^2 \cdot 3 \).
- Rewrite \( x^5 \) as \( x^4 \cdot x \) and \( y^2 \) as \( y^2 \).
- The expression becomes \( \sqrt{2^2 \cdot 3 \cdot x^4 \cdot x \cdot y^2} \).
- Simplify to \( 2x^2y \cdot \sqrt{3x} \).
The simplified form is \( 2x^2y \sqrt{3x} \).
Now, let's consider a more complex example involving multiple variables:
Simplify \( \sqrt{18a^3b^4c^2} \).
- Factorize \( 18 \) into \( 2 \cdot 3^2 \).
- Rewrite \( a^3 \) as \( a^2 \cdot a \), \( b^4 \) as \( (b^2)^2 \), and \( c^2 \) as \( c^2 \).
- The expression becomes \( \sqrt{2 \cdot 3^2 \cdot a^2 \cdot a \cdot b^4 \cdot c^2} \).
- Simplify to \( 3ab^2c \cdot \sqrt{2a} \).
The simplified form is \( 3ab^2c \sqrt{2a} \).
Examples and Practice Problems
In this section, we will go through various examples and practice problems to help you understand how to simplify square roots with variables. Follow along with the steps and use these examples to practice on your own.
Example 1: Simplifying the Square Root of a Single Variable
Let's start with a simple example involving a single variable.
\[\sqrt{x^4}\]
Step-by-Step Solution:
- Rewrite the expression: \[\sqrt{x^4} = \sqrt{(x^2)^2}\]
- Take the square root: \[x^2\]
- Final Answer: \[x^2\]
Example 2: Simplifying the Square Root of Multiple Variables
Now, let's simplify a square root that contains multiple variables.
\[\sqrt{x^4 y^2}\]
Step-by-Step Solution:
- Rewrite the expression: \[\sqrt{x^4 y^2} = \sqrt{(x^2)^2 (y)^2}\]
- Take the square root of each term: \[x^2 y\]
- Final Answer: \[x^2 y\]
Example 3: Simplifying the Square Root with Odd Exponents
Consider an example where the variable has an odd exponent.
\[\sqrt{x^5}\]
Step-by-Step Solution:
- Rewrite the expression: \[\sqrt{x^5} = \sqrt{x^4 \cdot x} = \sqrt{(x^2)^2 \cdot x}\]
- Take the square root of the perfect square: \[x^2 \sqrt{x}\]
- Final Answer: \[x^2 \sqrt{x}\]
Practice Problems
Try solving these practice problems on your own:
- \[\sqrt{x^6}\]
- \[\sqrt{y^8 z^2}\]
- \[\sqrt{16a^4 b^2}\]
- \[\sqrt{50x^3}\]
Solutions to Practice Problems
Here are the solutions to the practice problems:
- \[\sqrt{x^6} = x^3\]
- \[\sqrt{y^8 z^2} = y^4 z\]
- \[\sqrt{16a^4 b^2} = 4a^2 b\]
- \[\sqrt{50x^3} = 5x \sqrt{2x}\]

Special Cases and Common Mistakes
Simplifying square roots with variables can sometimes be tricky, especially when dealing with special cases and avoiding common mistakes. Here are some important tips and examples to help you navigate these challenges:
Special Cases
- Variables with Even Exponents: When the variable inside the square root has an even exponent, it can be simplified directly. For example:
\[\sqrt{x^6} = x^3\]
\[\sqrt{y^8} = y^4\] - Variables with Odd Exponents: When the variable has an odd exponent, split it into a product of an even exponent and the variable raised to the first power. For example:
\[\sqrt{x^7} = \sqrt{x^6 \cdot x} = x^3 \sqrt{x}\]
\[\sqrt{y^9} = \sqrt{y^8 \cdot y} = y^4 \sqrt{y}\] - Absolute Value Considerations: When taking the square root of a variable squared, always consider the absolute value to ensure the result is non-negative. For example:
\[\sqrt{x^2} = |x|\]
Common Mistakes
- Ignoring the Absolute Value: When simplifying \(\sqrt{x^2}\), the correct answer is \(|x|\), not just \(x\), because \(x\) could be negative.
- Incorrectly Simplifying Odd Exponents: Ensure you properly separate the odd exponent into an even exponent and the first power. For example, \(\sqrt{a^5}\) should be simplified as \(\sqrt{a^4 \cdot a} = a^2 \sqrt{a}\).
- Misidentifying Perfect Squares: When simplifying square roots with constants and variables, correctly identify perfect square factors. For example:
\[\sqrt{50x^2} = \sqrt{25 \cdot 2 \cdot x^2} = 5x\sqrt{2}\]
Example Problems
- Simplify \(\sqrt{36x^4}\):
\[\sqrt{36x^4} = \sqrt{36} \cdot \sqrt{x^4} = 6x^2\] - Simplify \(\sqrt{72y^3}\):
\[\sqrt{72y^3} = \sqrt{36 \cdot 2 \cdot y^2 \cdot y} = 6y\sqrt{2y}\] - Simplify \(\sqrt{49x^{10}y^8}\):
\[\sqrt{49x^{10}y^8} = \sqrt{49} \cdot \sqrt{x^{10}} \cdot \sqrt{y^8} = 7x^5y^4\]
Application in Algebraic Expressions
Applying the simplification of square roots with variables in algebraic expressions can make solving equations more manageable. Here are some steps and examples to illustrate this process:
Steps for Simplifying Square Roots in Algebraic Expressions
- Identify and separate any perfect square factors from the radicand (the expression under the square root).
- Use the properties of square roots to simplify the expression. The two main properties are:
- Product Property: \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\)
- Quotient Property: \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\), where \(b \neq 0\)
- Simplify the resulting expression by performing the operations on the numbers and variables separately.
- Combine like terms if applicable.
Examples
Example 1: Simplifying \(\sqrt{50x^2y^3z}\)
- Factor the radicand: \(50x^2y^3z = 25 \cdot 2 \cdot x^2 \cdot y^2 \cdot y \cdot z\)
- Separate the perfect squares: \(\sqrt{25 \cdot 2 \cdot x^2 \cdot y^2 \cdot y \cdot z} = \sqrt{25} \cdot \sqrt{2} \cdot \sqrt{x^2} \cdot \sqrt{y^2} \cdot \sqrt{y} \cdot \sqrt{z}\)
- Simplify each square root: \(5 \cdot \sqrt{2} \cdot x \cdot y \cdot \sqrt{y} \cdot \sqrt{z}\)
- Combine like terms: \(5xy\sqrt{2yz}\)
Example 2: Simplifying \(\sqrt{\frac{45a^6b^4}{5a^2b}}\)
- Simplify the fraction under the square root: \(\frac{45a^6b^4}{5a^2b} = 9a^4b^3\)
- Apply the square root: \(\sqrt{9a^4b^3} = \sqrt{9} \cdot \sqrt{a^4} \cdot \sqrt{b^3}\)
- Simplify each square root: \(3 \cdot a^2 \cdot \sqrt{b^3} = 3a^2b\sqrt{b}\)
Example 3: Simplifying \(\frac{\sqrt{72x^5}}{\sqrt{2x}}\)
- Combine the square roots: \(\frac{\sqrt{72x^5}}{\sqrt{2x}} = \sqrt{\frac{72x^5}{2x}} = \sqrt{36x^4}\)
- Simplify the square root: \(\sqrt{36x^4} = 6x^2\)
These examples demonstrate how to apply the properties of square roots to simplify expressions in algebra. By breaking down the expressions into smaller parts, you can manage and simplify complex algebraic expressions involving square roots.
FAQs and Troubleshooting Tips
Here are some frequently asked questions and troubleshooting tips to help you simplify square roots with variables effectively:
- Q: How do I simplify a square root with a single variable?
- Rewrite \( x^8 \) as \( (x^4)^2 \).
- Apply the square root to get \( x^4 \).
- Thus, \( \sqrt{x^8} = x^4 \).
- Q: What if the variable has an odd exponent?
- Rewrite \( x^9 \) as \( x^8 \cdot x \).
- Simplify \( \sqrt{x^8 \cdot x} = \sqrt{x^8} \cdot \sqrt{x} = x^4 \cdot \sqrt{x} \).
- Thus, \( \sqrt{x^9} = x^4 \sqrt{x} \).
- Q: How do I handle square roots with multiple variables?
- Rewrite each variable with even exponents and separate the odd parts: \( w \cdot x^8 \cdot x \cdot y^6 \cdot z^4 \cdot z \).
- Simplify the even parts: \( \sqrt{x^8} = x^4 \), \( \sqrt{y^6} = y^3 \), and \( \sqrt{z^4} = z^2 \).
- Combine the simplified parts with the remaining square roots: \( w \cdot x^4 \cdot y^3 \cdot z^2 \cdot \sqrt{xz} \).
- Thus, \( \sqrt{w \cdot x^9 \cdot y^6 \cdot z^5} = x^4 y^3 z^2 \sqrt{wxz} \).
- Q: How do I simplify a square root with a coefficient and variables?
- Factor 12 into prime factors: \( 12 = 2^2 \cdot 3 \).
- Rewrite the expression: \( \sqrt{2^2 \cdot 3 \cdot x^4 \cdot x \cdot y^2} \).
- Simplify the perfect squares: \( \sqrt{2^2} = 2 \), \( \sqrt{x^4} = x^2 \), \( \sqrt{y^2} = y \).
- Combine the simplified parts: \( 2x^2y \sqrt{3x} \).
- Thus, \( \sqrt{12x^5y^2} = 2x^2y \sqrt{3x} \).
- Q: What are common mistakes to avoid?
- Not factoring the exponents correctly.
- Forgetting to simplify coefficients separately.
- Ignoring absolute values for variables when necessary (e.g., \( \sqrt{x^2} = |x| \)).
A: To simplify a square root with a single variable, identify the largest square factor of the variable's exponent. For example, to simplify \( \sqrt{x^8} \):
A: When dealing with odd exponents, separate the variable into a product of even and odd exponents. For example, to simplify \( \sqrt{x^9} \):
A: Simplify each variable separately and then combine the results. For example, to simplify \( \sqrt{w \cdot x^9 \cdot y^6 \cdot z^5} \):
A: Factor the coefficient into its prime factors and simplify the variables separately. For example, to simplify \( \sqrt{12x^5y^2} \):
A: Some common mistakes include:
Additional Resources and References
For further reading and practice on simplifying square roots with variables, consider exploring the following resources:
-
Symbolab Study Guide: This comprehensive guide offers step-by-step solutions and examples for simplifying square roots with variables.
-
LibreTexts Mathematics: A detailed resource providing numerous examples and explanations on simplifying square roots, including variable expressions.
-
SparkNotes on Exponents: An insightful guide that covers the fundamental principles and provides practice problems to enhance your understanding.
-
Lumen Learning: Offers a developmental math emporium with in-depth lessons on identifying and simplifying roots, perfect for additional practice.
These resources will help reinforce your knowledge and provide additional practice problems to master the concept of simplifying square roots with variables.
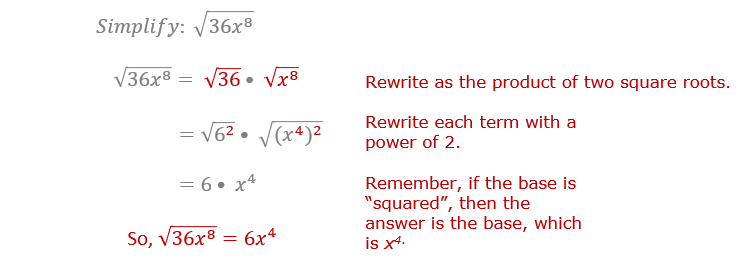
Video hướng dẫn đơn giản hóa căn bậc hai với biến số, giúp người xem hiểu rõ và nắm vững kiến thức về chủ đề này.
Căn bậc hai với biến số (Đơn giản hóa Toán học)
READ MORE:
Video hướng dẫn cách đơn giản hóa biểu thức căn bậc với biến số, giúp người xem hiểu rõ và nắm vững kỹ năng quan trọng này.
Đơn giản hóa biểu thức căn bậc với biến số