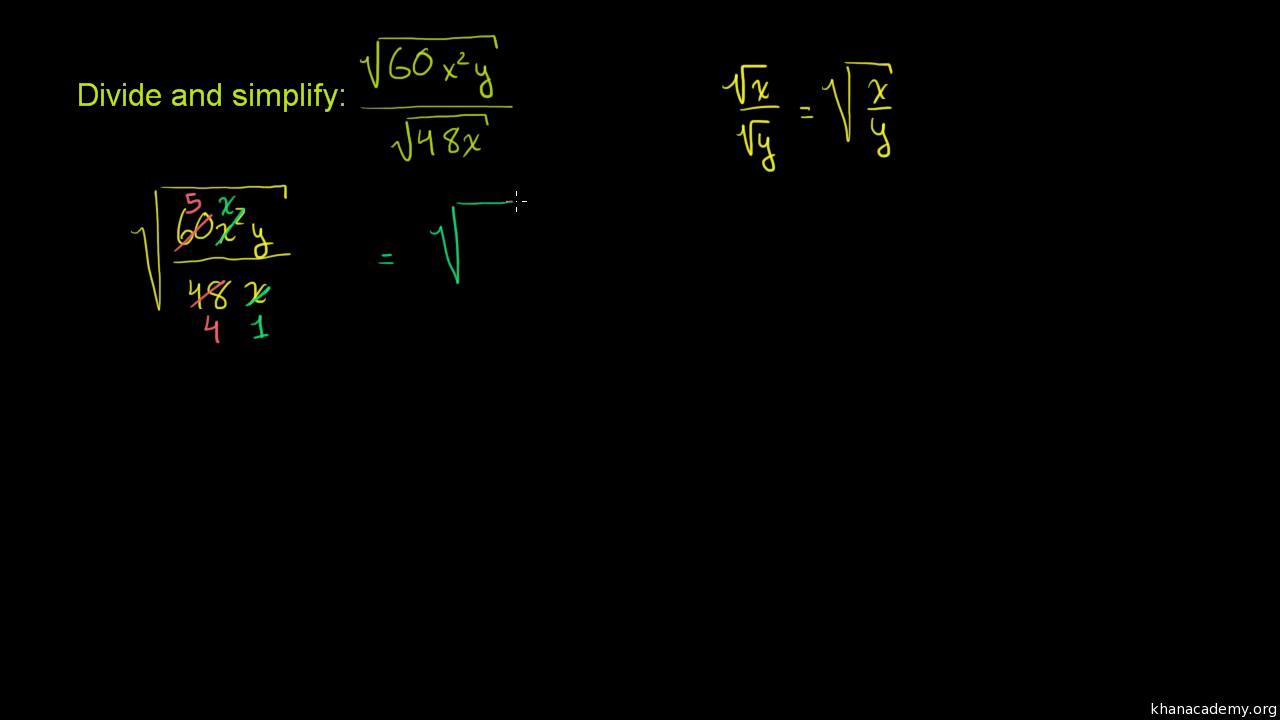How to Simplify Radical Expressions: Mastering the Basics and Beyond

Simplifying radical expressions involves several key steps to ensure the expression is in its simplest form. Below, we will explore the process in detail.

Steps to Simplify Radical Expressions

1. Identify and factor the radicand (the number under the radical sign).
2. Look for perfect square factors of the radicand.
3. Rewrite the radical expression using the factors.
4. Simplify the radical by taking the square root of the perfect square factors.

Examples

Let's look at a few examples to illustrate the process:

Example 1: Simplify \( \sqrt{50} \)

• Factor 50 into \( 25 \times 2 \).
• Rewrite the radical: \( \sqrt{50} = \sqrt{25 \times 2} \).
• Simplify by taking the square root of 25: \( \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} = 5\sqrt{2} \).

Example 2: Simplify \( \sqrt{72} \)

• Factor 72 into \( 36 \times 2 \).
• Rewrite the radical: \( \sqrt{72} = \sqrt{36 \times 2} \).
• Simplify by taking the square root of 36: \( \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} = 6\sqrt{2} \).

Example 3: Simplify \( \sqrt{128} \)

• Factor 128 into \( 64 \times 2 \).
• Rewrite the radical: \( \sqrt{128} = \sqrt{64 \times 2} \).
• Simplify by taking the square root of 64: \( \sqrt{64 \times 2} = \sqrt{64} \times \sqrt{2} = 8\sqrt{2} \).

Practice Problems

Try simplifying the following radical expressions:

1. \( \sqrt{98} \)
2. \( \sqrt{200} \)
3. \( \sqrt{18} \)

Summary

Simplifying radical expressions requires identifying perfect square factors, rewriting the radical, and simplifying. Practice these steps to become proficient in handling radical expressions.

Simplifying radical expressions involves reducing the expression to its simplest form. This process includes factoring the radicand, identifying perfect squares or cubes, and applying algebraic rules. Whether dealing with square roots or higher-order roots, understanding the methods to simplify these expressions can make complex calculations more manageable.

Here are the key steps and tips for simplifying radical expressions:

1. Identify the perfect square factors of the radicand. For example, in the expression \( \sqrt{72} \), both 4 and 9 are perfect square factors, but the largest one is 36.
2. Rewrite the radicand as a product of its factors: \( \sqrt{72} = \sqrt{36 \times 2} \).
3. Separate the square root into individual radicals: \( \sqrt{36} \times \sqrt{2} \).
4. Simplify the radicals: \( 6\sqrt{2} \).

When simplifying expressions with variables, treat the variables as you would numerical factors. For instance, \( \sqrt{x^2} = x \) if \( x \geq 0 \).

Here are some rules for simplifying radical expressions:

• \( \sqrt{ab} = \sqrt{a} \times \sqrt{b} \)
• \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}, b \neq 0 \)
• \( \sqrt{a} + \sqrt{b} \neq \sqrt{a + b} \)
• \( \sqrt{a} - \sqrt{b} \neq \sqrt{a - b} \)

For simplifying higher-order roots, the goal is to find factors under the radical that are perfect powers of the root. For example, to simplify \( \sqrt[3]{40m^5} \), find the factors of 40 that are perfect cubes and pair them with the variables accordingly.

In summary, simplifying radical expressions involves recognizing and factoring out perfect squares or cubes, applying algebraic rules, and carefully handling variables to achieve the simplest form of the expression.

Radicals, often represented by the square root symbol (√), are expressions that involve roots of numbers. To fully understand radicals, it's essential to grasp the concept of simplifying these expressions. Simplifying a radical means to find an equivalent expression where the radicand (the number inside the radical) has no perfect square factors other than 1.

There are several properties and rules that can help simplify radicals efficiently:

• Product Property: \( \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \)
• Quotient Property: \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}, \, b \neq 0 \)

To simplify a radical expression step by step:

1. Identify and factor the radicand into its prime factors.
2. Group the factors into pairs (for square roots), triplets (for cube roots), etc.
3. Rewrite the radical as the product of simpler radicals, separating out the perfect squares, cubes, etc.
4. Simplify the radicals by taking the root of the perfect squares, cubes, etc.

Let's look at an example:

By understanding and applying these properties, you can simplify any radical expression effectively. Practice with different examples to master the technique.

Simplifying radical expressions involves a few key steps to ensure that the expression is in its simplest form. Here are the basic steps:

1. Find the largest perfect square factor: Identify the largest perfect square that is a factor of the radicand (the number inside the radical). For example, for \( \sqrt{72} \), the largest perfect square factor is 36, because \( 72 = 36 \times 2 \).

2. Rewrite the radicand: Express the radicand as a product of the perfect square factor and another factor. For instance, \( \sqrt{72} \) can be rewritten as \( \sqrt{36 \times 2} \).

3. Apply the square root to the perfect square: Simplify the expression by taking the square root of the perfect square factor. Using the example, \( \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} = 6\sqrt{2} \).

4. Simplify further if needed: If the remaining radicand can be simplified further, repeat the process. For example, if you start with \( \sqrt{72} \) and use 9 as the perfect square factor, you get \( \sqrt{9 \times 8} = 3\sqrt{8} \). Then simplify \( \sqrt{8} \) to \( \sqrt{4 \times 2} = 2\sqrt{2} \), resulting in \( 3 \times 2\sqrt{2} = 6\sqrt{2} \).

5. Combine like terms: If you have multiple radical terms, combine them by adding or subtracting like terms. For example, \( 2\sqrt{3} + 3\sqrt{3} = 5\sqrt{3} \).

By following these steps, you can simplify radical expressions effectively and ensure they are in their simplest form.

When simplifying radical expressions, one key step is to identify the perfect square factors of the radicand (the number inside the radical). Perfect square factors are numbers that can be written as the square of an integer. For example, 1, 4, 9, 16, 25, and 36 are all perfect squares.

Follow these steps to identify and use perfect square factors in simplification:

1. Break down the radicand into its prime factors. This helps in identifying the perfect square factors.
2. Look for pairs of prime factors, since the product of each pair is a perfect square.
3. Factor the radicand into a product of perfect squares and other numbers. For instance, to simplify √72:
• Prime factorization of 72: 72 = 2 × 2 × 2 × 3 × 3
• Identify pairs: (2 × 2) and (3 × 3)
• Rewrite as a product of perfect squares: 72 = 4 × 9 × 2
4. Take the square root of each perfect square factor and simplify the radical expression. For √72:
• √72 = √(4 × 9 × 2) = √4 × √9 × √2 = 2 × 3 × √2 = 6√2
5. Combine the simplified terms. If there are variables, apply the same process by grouping them into pairs.

Identifying and using perfect square factors efficiently reduces the complexity of radical expressions and ensures that they are fully simplified.

Simplifying square roots involves expressing the radical in its simplest form. This often requires finding the largest perfect square factor of the radicand (the number inside the square root) and then simplifying.

1. Find the Perfect Square Factors:

   Identify the largest perfect square factor of the radicand. For example, to simplify \( \sqrt{72} \), notice that \( 36 \) is a perfect square factor.

   • \( \sqrt{72} = \sqrt{36 \times 2} \)

2. Separate the Radicand:

   Write the radicand as a product of the perfect square and the remaining factor.

   • \( \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} \)

3. Simplify the Square Root:

   Take the square root of the perfect square factor.

   • \( \sqrt{36} \times \sqrt{2} = 6\sqrt{2} \)

Let's look at another example:

1. Example: Simplify \( \sqrt{200} \)

   • Find the perfect square factor: \( 100 \) is a perfect square.
   • Express the radicand: \( \sqrt{200} = \sqrt{100 \times 2} \)
   • Simplify: \( \sqrt{100} \times \sqrt{2} = 10\sqrt{2} \)

Simplifying cube roots follows a similar approach to simplifying square roots, but instead of looking for pairs of identical factors, we look for triplets of identical factors. Here is a step-by-step guide to simplifying cube roots:

1. Factor the Radicand: Determine the prime factors of the number under the cube root.

   For example, let's simplify the cube root of 54: \( \sqrt[3]{54} \).

   The prime factorization of 54 is \( 54 = 2 \times 3^3 \).

2. Group the Factors: Group the factors into sets of three identical factors.

   \( \sqrt[3]{2 \times 3^3} = \sqrt[3]{2 \times (3^3)} \)

3. Simplify the Cube Root: Simplify by taking one factor out of the cube root for each group of three identical factors.

   \( \sqrt[3]{2 \times (3^3)} = 3 \times \sqrt[3]{2} \)

Thus, \( \sqrt[3]{54} = 3 \sqrt[3]{2} \).

Let’s consider another example:

Example: Simplify \( \sqrt[3]{216} \).

1. Prime factorize the number: \( 216 = 2^3 \times 3^3 \).

2. Group the factors into sets of three: \( \sqrt[3]{2^3 \times 3^3} \).

3. Simplify the cube root: \( \sqrt[3]{2^3 \times 3^3} = 2 \times 3 = 6 \).

Therefore, \( \sqrt[3]{216} = 6 \).

In cases where the radicand includes variables, apply the same steps:

Example: Simplify \( \sqrt[3]{27x^9y^6} \).

1. Prime factorize and expand the variables: \( 27x^9y^6 = 3^3 \times (x^3)^3 \times (y^3)^2 \).

2. Group the factors into sets of three: \( \sqrt[3]{3^3 \times (x^3)^3 \times (y^3)^2} \).

3. Simplify the cube root: \( \sqrt[3]{3^3 \times (x^3)^3 \times (y^3)^2} = 3 \times x^3 \times y^2 = 3x^3y^2 \).

Therefore, \( \sqrt[3]{27x^9y^6} = 3x^3y^2 \).

These steps can be applied to any cube root to simplify it to its simplest form.

Higher-order roots extend the concept of square roots and cube roots to any integer root. The nth root of a number a, written as \(\sqrt[n]{a}\), is a number that, when raised to the power of n, gives a. This can be summarized as follows:

1. For an odd n, the nth root of a negative number is negative. For example, \(\sqrt[3]{-27} = -3\) because \((-3)^3 = -27\).
2. For an even n, the nth root of a negative number is not a real number. For example, \(\sqrt[4]{-16}\) is undefined in the set of real numbers because there is no real number that, when raised to the fourth power, equals -16.

Steps to Simplify Higher-Order Roots

To simplify higher-order roots, follow these steps:

1. Identify the largest perfect power of the radicand that matches the root. For example, to simplify \(\sqrt[4]{81}\), recognize that \(81 = 3^4\).
2. Rewrite the radicand as the product of this perfect power and any remaining factors. For example, \(\sqrt[4]{81} = \sqrt[4]{(3^4)}\).
3. Simplify the root of the perfect power. Continuing the example, \(\sqrt[4]{(3^4)} = 3\).

Examples

Here are some examples to illustrate the process:

1. Simplify \(\sqrt[5]{32}\):
   • Recognize that \(32 = 2^5\).
   • Rewrite the expression: \(\sqrt[5]{32} = \sqrt[5]{(2^5)}\).
   • Simplify: \(\sqrt[5]{(2^5)} = 2\).
2. Simplify \(\sqrt[6]{64}\):
   • Recognize that \(64 = 2^6\).
   • Rewrite the expression: \(\sqrt[6]{64} = \sqrt[6]{(2^6)}\).
   • Simplify: \(\sqrt[6]{(2^6)} = 2\).
3. Simplify \(\sqrt[3]{-27}\):
   • Recognize that \(-27 = (-3)^3\).
   • Rewrite the expression: \(\sqrt[3]{-27} = \sqrt[3]{((-3)^3)}\).
   • Simplify: \(\sqrt[3]{((-3)^3)} = -3\).

Rational Exponents

Higher-order roots can also be expressed using rational exponents. The general rule is:

\(\sqrt[n]{a} = a^{1/n}\)

For example, \(\sqrt[4]{16} = 16^{1/4} = 2\) because \(2^4 = 16\).

Similarly, \(\sqrt[3]{8} = 8^{1/3} = 2\) because \(2^3 = 8\).

Practice Problems

Try simplifying these higher-order roots:

1. \(\sqrt[4]{256}\)
2. \(\sqrt[5]{32}\)
3. \(\sqrt[3]{-125}\)
4. \(\sqrt[6]{64}\)

Solutions:

1. \(\sqrt[4]{256} = 4\)
2. \(\sqrt[5]{32} = 2\)
3. \(\sqrt[3]{-125} = -5\)
4. \(\sqrt[6]{64} = 2\)

Combining like terms with radicals involves adding or subtracting radical expressions that have the same index and radicand. Here are the steps to follow:

1. Identify Like Radicals: Like radicals have the same index and the same radicand. For example, \(3\sqrt{2}\) and \(5\sqrt{2}\) are like radicals because they both have the square root of 2. Similarly, \(4\sqrt[3]{5}\) and \(2\sqrt[3]{5}\) are like radicals because they both have the cube root of 5.

2. Combine the Coefficients: To combine like radicals, add or subtract their coefficients while keeping the radical part unchanged.

   For example:

   • \(3\sqrt{2} + 5\sqrt{2} = (3 + 5)\sqrt{2} = 8\sqrt{2}\)
   • \(7\sqrt[3]{5} + 3\sqrt[3]{5} = (7 + 3)\sqrt[3]{5} = 10\sqrt[3]{5}\)
   • \(4\sqrt{10} - 5\sqrt{10} = (4 - 5)\sqrt{10} = -1\sqrt{10} = -\sqrt{10}\)

3. Simplify When Possible: If the radicals are not initially like terms, simplify them first to see if they can be combined. This involves breaking down the radicand to its prime factors and simplifying the radicals.

   For example:

   • \(3\sqrt{8} + 5\sqrt{2}\)

   Simplify \(\sqrt{8}\) to \(2\sqrt{2}\), then combine:

   • \(3 \cdot 2\sqrt{2} + 5\sqrt{2} = 6\sqrt{2} + 5\sqrt{2} = 11\sqrt{2}\)

4. Rearrange Terms if Needed: Sometimes, it helps to rearrange the terms to put like radicals next to each other before combining them.

   For example:

   • \(10\sqrt{5} + 6\sqrt{2} - 9\sqrt{5} - 7\sqrt{2}\)

   Rearrange and combine like terms:

   • \((10\sqrt{5} - 9\sqrt{5}) + (6\sqrt{2} - 7\sqrt{2}) = \sqrt{5} - \sqrt{2}\)

By following these steps, you can effectively combine like terms with radicals and simplify your expressions.

Rationalizing the denominator is the process of eliminating any irrational numbers (such as square roots) from the bottom of a fraction. This makes the expression simpler and easier to work with. Here's a step-by-step guide on how to rationalize the denominator:

1. Single Term Denominators:

   When the denominator is a single term, like \(\frac{1}{\sqrt{2}}\), you can multiply both the numerator and the denominator by the radical. For example:

   \[
   \frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}
   \]

2. Binomial Denominators:

   When the denominator is a binomial, such as \(\frac{1}{a + \sqrt{b}}\), you should multiply the numerator and the denominator by the conjugate of the denominator. The conjugate of \(a + \sqrt{b}\) is \(a - \sqrt{b}\). For example:

   \[
   \frac{1}{3 + \sqrt{2}} \times \frac{3 - \sqrt{2}}{3 - \sqrt{2}} = \frac{3 - \sqrt{2}}{(3)^2 - (\sqrt{2})^2} = \frac{3 - \sqrt{2}}{9 - 2} = \frac{3 - \sqrt{2}}{7}
   \]

   Here, we use the difference of squares formula: \((a + b)(a - b) = a^2 - b^2\).

3. More Complex Denominators:

   For more complex denominators, such as those involving multiple terms or nested radicals, the same principles apply, but the algebra can be more involved. Consider the example:

   \[
   \frac{\sqrt{6} - \sqrt{2}}{\sqrt{6} + \sqrt{2}} \times \frac{\sqrt{6} - \sqrt{2}}{\sqrt{6} - \sqrt{2}} = \frac{(\sqrt{6} - \sqrt{2})^2}{(\sqrt{6})^2 - (\sqrt{2})^2} = \frac{6 - 2\sqrt{12} + 2}{6 - 2} = \frac{8 - 2\sqrt{12}}{4} = 2 - \sqrt{3}
   \]

   By multiplying by the conjugate, we simplify the expression to a form with a rational denominator.

By rationalizing the denominator, we convert the expression to its simplest form, making it easier to handle in further calculations.

Simplifying radical expressions that contain variables follows a similar process to simplifying those with only numbers. The key steps involve recognizing and using the properties of exponents and radicals. Here's a detailed, step-by-step guide:

1. Identify the Exponent: Determine if the exponent is even or odd.

2. Even Exponents: If the exponent is even, the variable can be simplified directly by taking half of the exponent inside the radical.

   Example: Simplify \( \sqrt{x^{10}} \)

   • \( \sqrt{x^{10}} = x^{10/2} = x^5 \)

3. Odd Exponents: If the exponent is odd, subtract one to make it even, then simplify.

   Example: Simplify \( \sqrt{y^9} \)

   • Rewrite the expression: \( \sqrt{y^9} = \sqrt{y^8 \cdot y} \)
   • Separate the radicals: \( \sqrt{y^8} \cdot \sqrt{y} \)
   • Simplify: \( y^{8/2} \cdot \sqrt{y} = y^4 \sqrt{y} \)

4. Multiple Variables: If the expression contains multiple variables, simplify each variable separately.

   Example: Simplify \( \sqrt{x^6 y^3} \)

   • Identify the exponents: \( x^6 \) has an even exponent, and \( y^3 \) has an odd exponent.
   • Simplify each part: \( \sqrt{x^6} = x^3 \), \( \sqrt{y^3} = \sqrt{y^2 \cdot y} = y \sqrt{y} \)
   • Combine the results: \( x^3 y \sqrt{y} \)

5. Combine Simplified Parts: After simplifying each part, combine them back into a single expression.

These steps will help ensure that your radical expressions with variables are simplified correctly, making them easier to work with in further calculations.

Simplifying radical expressions can be challenging, and there are several common mistakes students often make. Avoiding these errors will help ensure accuracy and understanding. Here are some of the most frequent mistakes and how to avoid them:

1. Forgetting to Simplify the Radicand First: Always simplify the expression inside the radical (the radicand) before applying any radical properties.

   • Example: Simplify \( \sqrt{50} \)
   • Correct Approach: \( \sqrt{50} = \sqrt{25 \cdot 2} = 5\sqrt{2} \)

2. Misapplying the Product Rule: The product rule states that \( \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \). Make sure to apply it correctly.

   • Incorrect: \( \sqrt{4 + 9} = \sqrt{4} + \sqrt{9} = 2 + 3 = 5 \)
   • Correct: \( \sqrt{4 + 9} = \sqrt{13} \)

3. Incorrectly Combining Radicals: Only like radicals can be combined. Ensure the radicands are the same before combining.

   • Incorrect: \( \sqrt{2} + \sqrt{3} = \sqrt{5} \)
   • Correct: \( \sqrt{2} + \sqrt{2} = 2\sqrt{2} \)

4. Failing to Rationalize the Denominator: When the denominator contains a radical, multiply the numerator and denominator by the conjugate or the necessary term to eliminate the radical.

   • Example: Rationalize \( \frac{1}{\sqrt{2}} \)
   • Correct Approach: \( \frac{1}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2} \)

5. Ignoring Absolute Values: When simplifying even roots, remember that the result should be non-negative, and use absolute values if necessary.

   • Example: Simplify \( \sqrt{x^2} \)
   • Correct Approach: \( \sqrt{x^2} = |x| \)

6. Incorrectly Applying the Quotient Rule: The quotient rule states \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \). Ensure the rule is applied correctly.

   • Incorrect: \( \sqrt{\frac{4}{9}} = \frac{4}{3} \)
   • Correct: \( \sqrt{\frac{4}{9}} = \frac{\sqrt{4}}{\sqrt{9}} = \frac{2}{3} \)

By paying attention to these common mistakes and practicing careful, step-by-step simplification, you can improve your ability to simplify radical expressions accurately and efficiently.

Practice Problem 1: Simplify \( \sqrt{50} \)

• Step 1: Identify the perfect square factors of 50. \( 50 = 25 \times 2 \)
• Step 2: Write the square root as a product of the square roots. \( \sqrt{50} = \sqrt{25 \times 2} \)
• Step 3: Simplify the square root of the perfect square factor. \( \sqrt{25} = 5 \)
• Step 4: Combine the simplified square root with the remaining factor. \( \sqrt{50} = 5\sqrt{2} \)

Practice Problem 2: Simplify \( \sqrt[3]{54} \)

• Step 1: Identify the perfect cube factors of 54. \( 54 = 27 \times 2 \)
• Step 2: Write the cube root as a product of the cube roots. \( \sqrt[3]{54} = \sqrt[3]{27 \times 2} \)
• Step 3: Simplify the cube root of the perfect cube factor. \( \sqrt[3]{27} = 3 \)
• Step 4: Combine the simplified cube root with the remaining factor. \( \sqrt[3]{54} = 3\sqrt[3]{2} \)

Practice Problem 3: Simplify \( \sqrt{18x^4} \)

• Step 1: Separate the constant and variable parts. \( \sqrt{18x^4} = \sqrt{18} \times \sqrt{x^4} \)
• Step 2: Simplify the square root of the constant. \( \sqrt{18} = 3\sqrt{2} \)
• Step 3: Simplify the square root of the variable part. \( \sqrt{x^4} = x^2 \)
• Step 4: Combine the simplified parts. \( \sqrt{18x^4} = 3x^2\sqrt{2} \)

Practice Problem 4: Rationalize the denominator \( \frac{5}{\sqrt{3}} \)

• Step 1: Multiply the numerator and denominator by \( \sqrt{3} \). \( \frac{5}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} \)
• Step 2: Simplify the expression. \( \frac{5\sqrt{3}}{3} \)

Practice Problem 5: Simplify \( \sqrt{\frac{49}{16}} \)

• Step 1: Apply the property of square roots to a fraction. \( \sqrt{\frac{49}{16}} = \frac{\sqrt{49}}{\sqrt{16}} \)
• Step 2: Simplify the numerator and denominator. \( \sqrt{49} = 7 \) and \( \sqrt{16} = 4 \)
• Step 3: Combine the simplified parts. \( \sqrt{\frac{49}{16}} = \frac{7}{4} \)

Practice Problem 6: Simplify \( \sqrt{32a^6b^5} \)

• Step 1: Separate the constant and variable parts. \( \sqrt{32a^6b^5} = \sqrt{32} \times \sqrt{a^6} \times \sqrt{b^5} \)
• Step 2: Simplify the square root of the constant. \( \sqrt{32} = 4\sqrt{2} \)
• Step 3: Simplify the square root of the variable parts. \( \sqrt{a^6} = a^3 \) and \( \sqrt{b^5} = b^2\sqrt{b} \)
• Step 4: Combine the simplified parts. \( \sqrt{32a^6b^5} = 4a^3b^2\sqrt{2b} \)

In this section, we will explore advanced techniques for simplifying radical expressions. These methods build upon the basic steps and provide more sophisticated tools to handle complex radicals.

1. Simplifying Radicals with Higher-Order Exponents

When dealing with higher-order roots, such as fourth or fifth roots, the process involves similar steps to simplifying square roots but with higher exponents.

For example, to simplify \( \sqrt[4]{16x^8} \):

1. Identify perfect fourth power factors: \[ \sqrt[4]{16x^8} = \sqrt[4]{(2^4)(x^8)} \]
2. Extract the fourth root of each factor: \[ \sqrt[4]{2^4} = 2 \] \[ \sqrt[4]{x^8} = x^2 \]
3. Combine the results: \[ \sqrt[4]{16x^8} = 2x^2 \]

2. Rationalizing the Denominator with Higher-Order Roots

When a radical expression has a higher-order root in the denominator, rationalizing involves multiplying by a conjugate or an appropriate form to eliminate the radical.

For example, to rationalize the denominator of \( \frac{1}{\sqrt[3]{2}} \):

1. Multiply the numerator and the denominator by \( \sqrt[3]{4} \) to make the exponent in the denominator a multiple of 3: \[ \frac{1}{\sqrt[3]{2}} \times \frac{\sqrt[3]{4}}{\sqrt[3]{4}} = \frac{\sqrt[3]{4}}{\sqrt[3]{8}} = \frac{\sqrt[3]{4}}{2} \]

3. Combining Radicals Using Common Denominators

When adding or subtracting radicals, they must have the same radicand (the number inside the radical). If they do not, you need to simplify them or find a common denominator.

For example, to combine \( \sqrt{2} + \sqrt{8} \):

1. Simplify each radical: \[ \sqrt{8} = \sqrt{4 \cdot 2} = 2\sqrt{2} \]
2. Combine like terms: \[ \sqrt{2} + 2\sqrt{2} = 3\sqrt{2} \]

4. Using Conjugates to Simplify Complex Radicals

For complex radicals involving binomials, multiplying by the conjugate can help simplify the expression. The conjugate of \( a + b\sqrt{c} \) is \( a - b\sqrt{c} \).

For example, to simplify \( \frac{1}{2 + \sqrt{3}} \):

1. Multiply the numerator and the denominator by the conjugate of the denominator: \[ \frac{1}{2 + \sqrt{3}} \times \frac{2 - \sqrt{3}}{2 - \sqrt{3}} = \frac{2 - \sqrt{3}}{(2 + \sqrt{3})(2 - \sqrt{3})} \]
2. Simplify the denominator: \[ (2 + \sqrt{3})(2 - \sqrt{3}) = 4 - 3 = 1 \]
3. Combine the results: \[ \frac{2 - \sqrt{3}}{1} = 2 - \sqrt{3} \]

5. Simplifying Radical Expressions with Variables

When simplifying radicals with variables, apply the same principles while considering the exponents of the variables.

For example, to simplify \( \sqrt{x^4 y^6} \):

1. Rewrite the expression with fractional exponents: \[ \sqrt{x^4 y^6} = (x^4 y^6)^{1/2} \]
2. Distribute the exponent: \[ x^{4/2} y^{6/2} = x^2 y^3 \]

Radical expressions have numerous applications in various fields, from engineering to physics, and even finance. Below are some common applications where radicals are essential:

1. Geometry and Trigonometry

Radical expressions are frequently used to calculate distances, areas, and volumes. For example, the Pythagorean theorem involves square roots to find the length of the hypotenuse in a right triangle:

\[ c = \sqrt{a^2 + b^2} \]

2. Physics

In physics, radicals are used to describe wave functions, energy levels, and distances. For example, the formula for the period \(T\) of a pendulum involves a square root:

\[ T = 2\pi \sqrt{\frac{L}{g}} \]

where \(L\) is the length of the pendulum and \(g\) is the acceleration due to gravity.

3. Engineering

Engineers use radical expressions in various calculations, such as determining stress and strain on materials. The formula for the natural frequency of a beam involves square roots:

\[ f = \frac{1}{2\pi} \sqrt{\frac{k}{m}} \]

where \(k\) is the stiffness and \(m\) is the mass.

4. Finance

In finance, radicals are used to calculate compound interest and annuities. The formula for continuously compounded interest involves the exponential function, which can be related to radicals:

\[ A = P e^{rt} \]

where \(P\) is the principal amount, \(r\) is the rate, and \(t\) is time. Simplifying this can involve roots in certain steps.

5. Computer Science

Radical expressions are used in algorithms and computational complexity. For example, the time complexity of certain algorithms involves square roots, such as in the case of the square root algorithm for finding the median of two sorted arrays.

6. Medicine

In medicine, radicals are used in pharmacokinetics to determine drug dosage and concentration over time. The formula for the half-life of a drug involves a logarithm, which can be simplified using radical expressions:

\[ t_{1/2} = \frac{\ln(2)}{k} \]

where \(k\) is the elimination rate constant.

7. Environmental Science

Radicals are used to model population growth, pollutant dispersion, and other natural phenomena. The formula for the diffusion rate of a substance in a medium involves square roots:

\[ D = \sqrt{\frac{2kT}{\pi m}} \]

where \(D\) is the diffusion coefficient, \(k\) is the Boltzmann constant, \(T\) is the temperature, and \(m\) is the mass of the particle.

These examples illustrate the versatility and importance of radical expressions in various real-world applications, showcasing their relevance beyond pure mathematics.

In this section, we will summarize the key points discussed throughout the guide on simplifying radical expressions.

Key Concepts

• Radical expressions include roots such as square roots, cube roots, and higher-order roots.
• To simplify a radical expression, identify and extract perfect square (or higher power) factors.

Basic Steps to Simplify Radical Expressions

1. Identify the radicand (the number inside the radical).
2. Factor the radicand into its prime factors.
3. Look for pairs (or groups corresponding to the root) of factors.
4. Move pairs of factors outside the radical.
5. Simplify the remaining expression inside the radical.

Examples

Here are some examples to illustrate the simplification process:

Example 1: Simplifying Square Roots

Simplify: \( \sqrt{72} \)

1. Factor 72 into prime factors: \( 72 = 2 \times 2 \times 2 \times 3 \times 3 \)
2. Group pairs of prime factors: \( \sqrt{72} = \sqrt{(2 \times 2) \times (3 \times 3) \times 2} \)
3. Extract pairs as single factors: \( \sqrt{72} = 2 \times 3 \times \sqrt{2} \)
4. Simplify: \( \sqrt{72} = 6\sqrt{2} \)

Example 2: Simplifying Cube Roots

Simplify: \( \sqrt[3]{27x^3} \)

1. Factor the radicand: \( 27x^3 = 3^3 \times x^3 \)
2. Extract the cube root of each factor: \( \sqrt[3]{27x^3} = \sqrt[3]{3^3} \times \sqrt[3]{x^3} \)
3. Simplify: \( \sqrt[3]{27x^3} = 3x \)

Example 3: Simplifying Higher-Order Roots

Simplify: \( \sqrt[4]{16y^4} \)

1. Factor the radicand: \( 16y^4 = 2^4 \times y^4 \)
2. Extract the fourth root of each factor: \( \sqrt[4]{16y^4} = \sqrt[4]{2^4} \times \sqrt[4]{y^4} \)
3. Simplify: \( \sqrt[4]{16y^4} = 2y \)

Important Rules

• Product Property: \( \sqrt[n]{a \cdot b} = \sqrt[n]{a} \cdot \sqrt[n]{b} \)
• Quotient Property: \( \sqrt[n]{\frac{a}{b}} = \frac{\sqrt[n]{a}}{\sqrt[n]{b}} \)
• Combining Radicals: Only like radicals (same radicand and index) can be combined.
• Rationalizing the Denominator: Eliminate radicals from the denominator by multiplying by a conjugate or an appropriate form of 1.

Common Mistakes to Avoid

• Combining unlike radicals.
• Forgetting to rationalize the denominator.
• Incorrectly factoring the radicand.

Final Thoughts

Simplifying radical expressions is a fundamental skill in algebra that can help solve complex equations and understand advanced mathematical concepts. Practice regularly to master the process and avoid common pitfalls.

Practice Problems

• Simplify: \( \sqrt{50} \)
• Simplify: \( \sqrt[3]{54} \)
• Simplify: \( \sqrt[4]{81x^4} \)

For further study and practice on simplifying radical expressions, consider exploring the following resources:

• This comprehensive video tutorial covers the basics of simplifying radical expressions, including examples and practice problems.

• This textbook-style resource provides detailed explanations, definitions, and numerous examples of simplifying radical expressions using properties of roots.

• ChiliMath offers step-by-step instructions and examples for simplifying various types of radical expressions, including those with numerical and variable components.

• Purplemath provides a detailed tutorial on simplifying radical expressions, with a focus on understanding the rules and properties of radicals.

• PatrickJMT features a series of instructional videos that break down the process of simplifying radical expressions in an easy-to-follow manner.

These resources offer a variety of instructional methods, from video tutorials to written explanations, ensuring that you can find the help you need to master simplifying radical expressions.