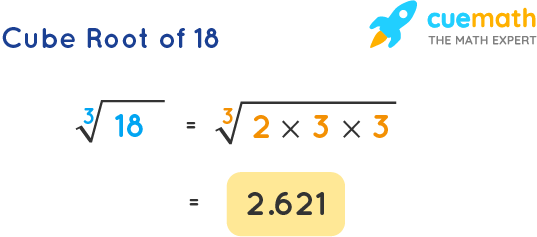
Topic what is the square root of 1: The square root of 1 is a fundamental concept in mathematics, often explored by students and enthusiasts alike. In this article, we will delve into what the square root of 1 is, its mathematical properties, and its significance in various contexts, providing a comprehensive understanding for readers of all levels.
Table of Content
- What is the square root of 1?
- Introduction to Square Roots
- Defining the Square Root
- Mathematical Explanation of the Square Root of 1
- Properties of the Number 1
- Positive and Negative Square Roots
- Square Root in Different Mathematical Contexts
- Applications of Square Roots in Real Life
- Square Root of 1 in Algebra
- Imaginary and Complex Numbers
- Square Root of 1 in Geometry
- Conclusion
- YOUTUBE: Tìm hiểu về căn bậc hai của –1, một khái niệm quan trọng trong toán học và số phức. Video này sẽ giúp bạn hiểu rõ hơn về khái niệm này.
What is the square root of 1?
The square root of 1 is a mathematical concept where a number, when multiplied by itself, equals 1. For real numbers, the square root of 1 can be either 1 or -1.
Key Points:
- The principal square root of 1 is +1.
- Another square root of 1 is -1.
- Both +1 and -1 satisfy the equation \( x^2 = 1 \).
Properties:
| Square of +1: | \( 1^2 = 1 \) |
| Square of -1: | \( (-1)^2 = 1 \) |

READ MORE:
Introduction to Square Roots
The concept of square roots is fundamental in mathematics and is used extensively in various fields. A square root of a number \( x \) is a number \( y \) such that \( y^2 = x \). For example, the square root of 9 is 3, because \( 3^2 = 9 \). Square roots can be both positive and negative, as both 3 and -3 are square roots of 9.
Square roots are often represented using the radical symbol \( \sqrt{} \). The expression \( \sqrt{x} \) denotes the principal (non-negative) square root of \( x \). In general, the square roots of a number can be described as:
- Positive square root: \( \sqrt{x} \)
- Negative square root: \( -\sqrt{x} \)
Here are some key properties of square roots:
- \(\sqrt{x^2} = |x| \) for any real number \( x \)
- \(\sqrt{ab} = \sqrt{a} \cdot \sqrt{b} \) for any non-negative numbers \( a \) and \( b \)
- \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \) for any non-negative numbers \( a \) and \( b \), with \( b \neq 0 \)
In the context of complex numbers, the square root function can be extended to all complex numbers. However, for real numbers, the square root function is defined only for non-negative values.
Understanding square roots is crucial for solving quadratic equations, analyzing geometric shapes, and working with various algebraic expressions. The square root of 1, specifically, is a unique case that serves as a fundamental example due to its simplicity and clear properties.
Defining the Square Root
The square root of a number is a value that, when multiplied by itself, gives the original number. Mathematically, if \( y \) is the square root of \( x \), then \( y^2 = x \). This relationship can be written as:
\[
y = \sqrt{x} \quad \text{such that} \quad y^2 = x
\]
For example:
- The square root of 4 is 2 because \( 2^2 = 4 \).
- The square root of 9 is 3 because \( 3^2 = 9 \).
The square root symbol \( \sqrt{} \) is used to represent the principal square root, which is the non-negative root. For example, \( \sqrt{4} = 2 \).
However, every positive number actually has two square roots: one positive and one negative. For example:
- \(\sqrt{4} = 2 \) and \(-\sqrt{4} = -2 \) because \( (-2)^2 = 4 \).
The number 1 is unique in this regard because its square roots are both 1 and -1. This can be shown as:
- \(\sqrt{1} = 1 \) because \( 1^2 = 1 \)
- \(-\sqrt{1} = -1 \) because \( (-1)^2 = 1 \)
In summary, the square root function is a fundamental concept in mathematics that provides the basis for solving equations and understanding various mathematical properties. The special case of the square root of 1 highlights the simplicity and symmetry of this function.
Mathematical Explanation of the Square Root of 1
The square root of a number \( x \) is a value \( y \) such that \( y^2 = x \). For the number 1, the square roots are the numbers that satisfy the equation:
\[ y^2 = 1 \]
There are two numbers that satisfy this equation:
- \( y = 1 \)
- \( y = -1 \)
Thus, the square root of 1 is both 1 and -1. This is because:
- \( 1 \times 1 = 1 \)
- \( -1 \times -1 = 1 \)
In general, every positive real number has two square roots: one positive (known as the principal square root) and one negative. For the number 1, these are:
\[ \sqrt{1} = 1 \quad \text{and} \quad -\sqrt{1} = -1 \]
When we refer to the square root of 1 without any additional context, we usually mean the principal (positive) square root:
\[ \sqrt{1} = 1 \]
Properties of the Number 1
The number 1 has unique properties that make it an interesting subject in mathematics. It is the multiplicative identity, meaning any number multiplied by 1 remains unchanged. Additionally, the square of 1 is always 1:
\[ 1^2 = 1 \]
Square Root of 1 in Different Mathematical Contexts
In the context of complex numbers, the concept of square roots extends to include imaginary numbers. The square root of -1 is represented by the imaginary unit \( i \), where:
\[ i^2 = -1 \]
However, for the real number 1, its square roots remain the real numbers 1 and -1.
Properties of the Number 1
The number 1 holds a unique place in mathematics due to its distinct properties. Here are some of the key characteristics of the number 1:
- One is the first non-zero natural number and the first positive integer.
- It is an odd number.
- One is neither a prime number nor a composite number.
- It is the identity element for multiplication, meaning any number multiplied by 1 remains unchanged: \( a \times 1 = a \).
- One is its own factorial: \( 1! = 1 \).
- It is the only number that is its own square and square root: \( 1^2 = 1 \) and \( \sqrt{1} = 1 \).
- One is its own cube and cube root: \( 1^3 = 1 \) and \( \sqrt[3]{1} = 1 \).
- It is a regular number and a Fibonacci number.
- The natural logarithm of 1 is zero: \( \ln(1) = 0 \).
- The decimal logarithm of 1 is also zero: \( \log_{10}(1) = 0 \).
- One is the probability of an event that is almost certain to occur.
- One is the only positive integer that is divisible by exactly one positive integer.
- One is the only number written in the reverse alphabetical sequence of letters: O – N – E.
These properties highlight the fundamental role of the number 1 in various mathematical contexts and its unique position in the set of natural numbers.

Positive and Negative Square Roots
Understanding the concept of positive and negative square roots is essential in mathematics. When we talk about the square root of a number, we usually refer to the principal square root, which is the non-negative root. However, every positive real number actually has two square roots: one positive and one negative.
- The principal square root is denoted by the radical sign (√).
- The negative square root is denoted by placing a negative sign in front of the radical (−√).
For example, consider the number 1:
- The positive square root of 1 is \( \sqrt{1} = 1 \).
- The negative square root of 1 is \( -\sqrt{1} = -1 \).
In general, for any positive number \( x \), the square roots can be expressed as:
\[
\pm \sqrt{x}
\]
This means that both \( \sqrt{x} \) and \( -\sqrt{x} \) are solutions to the equation \( x^2 = x \).
Consider the equation \( x^2 = 9 \):
- Taking the square root of both sides, we get \( \pm \sqrt{9} \).
- Since \( \sqrt{9} = 3 \), the solutions are \( x = 3 \) and \( x = -3 \).
The use of the plus-minus sign (±) is a convenient way to represent both the positive and negative square roots simultaneously. This notation ensures that we consider all possible solutions in equations involving square roots.
In conclusion, while the radical sign (√) typically represents the principal (positive) square root, it is important to remember that every positive number has both a positive and a negative square root. This dual nature is crucial for solving equations and understanding the properties of numbers in mathematics.
Square Root in Different Mathematical Contexts
The concept of the square root is fundamental in various branches of mathematics. Understanding the square root of 1 provides insight into different mathematical contexts, from real numbers to complex numbers and beyond. Below are some key contexts where the square root of 1 is explored:
- Real Numbers
In the realm of real numbers, the square root of 1 is straightforward. Both 1 and -1 are solutions because:
\(\sqrt{1} = 1\) and \(\sqrt{1} = -1\)
Both these values satisfy the equation \(x^2 = 1\).
- Complex Numbers
In the context of complex numbers, the square root function can be extended to complex numbers. For any complex number \(z = x + iy\), the square roots are given by:
\(\sqrt{x + iy} = \pm (x^2 + y^2)^{1/4} \left( \cos\left( \frac{1}{2} \tan^{-1}\left(\frac{y}{x}\right) \right) + i \sin\left( \frac{1}{2} \tan^{-1}\left(\frac{y}{x}\right) \right) \right)\)
This formula showcases the complexity and richness of square roots in the field of complex numbers.
- Matrix Algebra
In matrix algebra, the concept of a square root extends to matrices. A matrix \(A\) is said to have a square root \(B\) if \(B^2 = A\). For instance, the identity matrix \(I\) has multiple square roots, including itself and the negative identity matrix:
\(I = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\)
\(B = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\) or \(B = \begin{bmatrix} -1 & 0 \\ 0 & -1 \end{bmatrix}\)
- Algebraic Structures
In various algebraic structures, such as fields and rings, the square root of 1 plays a significant role. For example, in modular arithmetic, the square root of 1 modulo \(n\) can have different interpretations depending on the value of \(n\).
Understanding the square root of 1 across these contexts enhances our comprehension of its properties and applications in diverse mathematical areas.
Applications of Square Roots in Real Life
Square roots have numerous applications in various fields, demonstrating their importance in everyday life. Here are some key applications:
-
Geometry:
In geometry, square roots are used to calculate the length of the sides of right triangles using the Pythagorean theorem. For instance, to find the hypotenuse \( c \) of a right triangle with legs \( a \) and \( b \), we use the formula \( c = \sqrt{a^2 + b^2} \).
-
Distance Calculation:
Square roots are essential in calculating the distance between two points in a plane or space. The distance \( D \) between points \((x_1, y_1)\) and \((x_2, y_2)\) is given by \( D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \). In three dimensions, it extends to \( D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2} \).
-
Finance:
In finance, square roots are used to calculate stock market volatility. The standard deviation, a measure of volatility, is derived from the square root of the variance. This helps investors assess the risk associated with different investments.
-
Physics:
Square roots appear in various physics formulas, such as calculating the root mean square (RMS) speed of gas molecules, which is essential for understanding kinetic theory. The RMS speed \( v_{rms} \) is given by \( v_{rms} = \sqrt{\frac{3kT}{m}} \), where \( k \) is the Boltzmann constant, \( T \) is the temperature, and \( m \) is the mass of a molecule.
-
Engineering:
In engineering, square roots are used to determine the natural frequencies of structures, which is crucial for ensuring the stability and integrity of buildings and bridges under various loads.
-
Statistics:
Square roots are fundamental in statistics for calculating the standard deviation, which measures the dispersion of a data set. The standard deviation \( \sigma \) is given by \( \sigma = \sqrt{\frac{1}{N}\sum_{i=1}^{N}(x_i - \mu)^2} \), where \( N \) is the number of observations, \( x_i \) is each individual observation, and \( \mu \) is the mean of the observations.
-
Computer Graphics:
Square roots are used in computer graphics to calculate distances and lengths, essential for rendering images and animations. For example, the length of a vector \( \vec{v} \) with components \( (v_x, v_y, v_z) \) is \( |\vec{v}| = \sqrt{v_x^2 + v_y^2 + v_z^2} \).
-
Cryptography:
In cryptography, algorithms often use square roots to encrypt and decrypt data, ensuring secure communication. For instance, some public-key cryptosystems are based on the difficulty of computing square roots modulo a composite number.
-
Navigation:
Square roots are used in navigation to calculate the shortest path between two points. For example, pilots use square roots to determine the distance and bearing between waypoints in flight planning.
These examples illustrate the wide-ranging importance of square roots in different fields, highlighting their practical applications and relevance in solving real-world problems.
Square Root of 1 in Algebra
In algebra, understanding the square root of 1 is fundamental as it provides insights into more complex algebraic concepts. The square root of a number \( x \) is a number \( y \) such that \( y^2 = x \). Therefore, for \( x = 1 \), we have \( y^2 = 1 \), leading to two solutions: \( y = 1 \) and \( y = -1 \).
The equation can be expressed as:
\[\sqrt{1} = \pm 1\]
This implies that both \( 1 \) and \( -1 \) are square roots of 1. This property is crucial in various algebraic manipulations and solving quadratic equations.
Solving Quadratic Equations
Quadratic equations often require finding square roots. For example, consider the equation:
\[x^2 - 2x + 1 = 0\]
This can be rewritten as:
\[(x - 1)^2 = 0\]
Taking the square root of both sides, we get:
\[x - 1 = 0 \implies x = 1\]
Complex Numbers
In the realm of complex numbers, the square root of 1 plays a role in understanding imaginary and complex solutions. For any real number \( x \), the principal square root is the non-negative solution. However, in complex numbers, we also consider the negative counterpart.
For example, the square root of -1 is denoted by \( i \), where:
\[i^2 = -1\]
Square Root Properties in Algebra
Several properties of square roots are useful in algebraic manipulations:
- \(\sqrt{ab} = \sqrt{a} \cdot \sqrt{b}\)
- \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
- \((\sqrt{a})^2 = a\)
Algebraic Applications
The concept of square roots extends beyond real numbers. In algebra, the properties of square roots are used in solving polynomial equations, simplifying expressions, and in the field of differential equations.
Example Problem
Solve the equation:
\[\sqrt{x+3} = 2\]
Square both sides:
\[x + 3 = 4\]
Subtract 3 from both sides:
\[x = 1\]
Understanding the square root of 1 and its properties is fundamental in algebra, paving the way for more advanced mathematical concepts and applications.

Imaginary and Complex Numbers
Imaginary and complex numbers extend the concept of one-dimensional real numbers to the two-dimensional complex plane by introducing the imaginary unit, denoted as i, where \( i^2 = -1 \). A complex number is expressed in the form \( a + bi \), where \( a \) and \( b \) are real numbers.
Basic Properties
Complex numbers have both a real part (\( a \)) and an imaginary part (\( b \)). They can be added, subtracted, multiplied, and divided, similar to polynomials, with the additional rule that \( i^2 = -1 \).
Operations with Complex Numbers
- Addition: \( (a + bi) + (c + di) = (a + c) + (b + d)i \)
- Subtraction: \( (a + bi) - (c + di) = (a - c) + (b - d)i \)
- Multiplication: \( (a + bi)(c + di) = ac + adi + bci + bdi^2 = (ac - bd) + (ad + bc)i \)
- Division: \(\frac{a + bi}{c + di} = \frac{(a + bi)(c - di)}{(c + di)(c - di)} = \frac{(ac + bd) + (bc - ad)i}{c^2 + d^2} \)
Complex Conjugate
The complex conjugate of a complex number \( z = a + bi \) is \( \overline{z} = a - bi \). It is useful in simplifying the division of complex numbers.
Geometric Representation
In the complex plane, a complex number \( a + bi \) is represented as a point or a vector from the origin to the point \( (a, b) \). The magnitude (or modulus) of a complex number \( z = a + bi \) is given by \( |z| = \sqrt{a^2 + b^2} \), and the argument (or angle) is \( \theta = \tan^{-1}\left(\frac{b}{a}\right) \).
Polar Form
A complex number can also be expressed in polar form as \( z = r(\cos \theta + i \sin \theta) \), where \( r = |z| \) and \( \theta \) is the argument. Using Euler's formula, it can be written as \( z = re^{i\theta} \).
Applications
Complex numbers have wide applications in various fields such as engineering, physics, and applied mathematics. They are essential in solving differential equations, analyzing electrical circuits, and describing oscillations and waveforms.
In summary, understanding imaginary and complex numbers is crucial for advanced mathematical concepts and practical applications in science and engineering.
Square Root of 1 in Geometry
The square root of 1, denoted as \( \sqrt{1} \), has a special place in geometry. It is often considered in various geometric constructions and theorems. Here, we explore several contexts where \( \sqrt{1} \) is relevant in geometry.
Unit Circle
In the unit circle, a circle with a radius of 1 centered at the origin of a coordinate system, the square root of 1 is significant. Any point on the circumference of this circle has coordinates \((x, y)\) such that \( x^2 + y^2 = 1 \). The radius of the unit circle is \( \sqrt{1} \), illustrating that any radius vector from the center to the circumference is exactly 1 unit long.
Pythagorean Theorem
The Pythagorean theorem states that in a right-angled triangle, the square of the hypotenuse \( c \) is equal to the sum of the squares of the other two sides \( a \) and \( b \), expressed as \( a^2 + b^2 = c^2 \). For a triangle where both sides \( a \) and \( b \) are 1, the hypotenuse \( c \) would be \( \sqrt{1^2 + 1^2} = \sqrt{2} \). Here, \( \sqrt{1} \) plays a role as the side lengths.
Geometric Mean
In geometry, the concept of the geometric mean can involve the square root of 1. If you have two segments of lengths \( a \) and \( b \), the geometric mean is \( \sqrt{ab} \). For \( a = 1 \) and \( b = 1 \), the geometric mean is \( \sqrt{1 \cdot 1} = 1 \).
Distance Formula
The distance formula, derived from the Pythagorean theorem, is used to find the distance between two points \((x_1, y_1)\) and \((x_2, y_2)\) in a plane, given by \( \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \). When the coordinates differ by 1 unit along either the x-axis or y-axis, the resulting distance includes the square root of 1. For instance, the distance between \((0, 0)\) and \((1, 0)\) is \( \sqrt{(1-0)^2 + (0-0)^2} = \sqrt{1} = 1 \).
Constructing Perpendicular Lines
Using geometric tools like a compass and straightedge, constructing perpendicular lines often involves unit lengths. For example, constructing a perpendicular bisector of a segment involves finding the midpoint and drawing a circle with a radius of \( \sqrt{1} = 1 \), ensuring that each half is equal.
Overall, \( \sqrt{1} \) frequently appears in geometric contexts, underscoring the fundamental nature of unity and distance in geometric constructions and theorems.
Conclusion
The square root of 1 is a fundamental concept in mathematics that reveals important properties about the number 1 and its role in various mathematical contexts. By understanding the square root of 1, we can gain deeper insights into algebra, geometry, and other branches of mathematics. Below are the key points summarizing the concepts discussed:
- Definition: The square root of a number is a value that, when multiplied by itself, gives the original number. For 1, the square roots are 1 and -1 because \(1^2 = 1\) and \((-1)^2 = 1\).
- Properties: The number 1 is unique in that it is the only positive integer whose square root is both 1 and -1. This dual nature plays a crucial role in solving equations and understanding symmetries.
- Positive and Negative Roots: While the principal square root of 1 is 1, acknowledging the negative square root (-1) is important for completeness in mathematical solutions and theoretical explorations.
- Mathematical Contexts: The square root of 1 appears in various mathematical areas, such as:
- Algebra: Used in solving quadratic equations and simplifying expressions.
- Geometry: Relevant in defining distances and transformations.
- Complex Numbers: Understanding the square roots of negative numbers builds on the concept of the square root of 1.
- Real-life Applications: Square roots are used in fields such as engineering, physics, and finance, where precise calculations and understanding of magnitudes are essential.
In conclusion, the square root of 1 serves as a cornerstone in mathematics, offering insights that extend beyond basic arithmetic to more complex theoretical frameworks. By appreciating both the positive and negative roots, we can better grasp the structure and relationships within mathematics.
Tìm hiểu về căn bậc hai của –1, một khái niệm quan trọng trong toán học và số phức. Video này sẽ giúp bạn hiểu rõ hơn về khái niệm này.
Căn bậc hai của –1 là gì?
READ MORE:
Tìm hiểu về căn bậc hai của số 1 và các tính chất liên quan.
Căn bậc hai của số 1 | Toán học cùng SQUARE ROOT OF 1