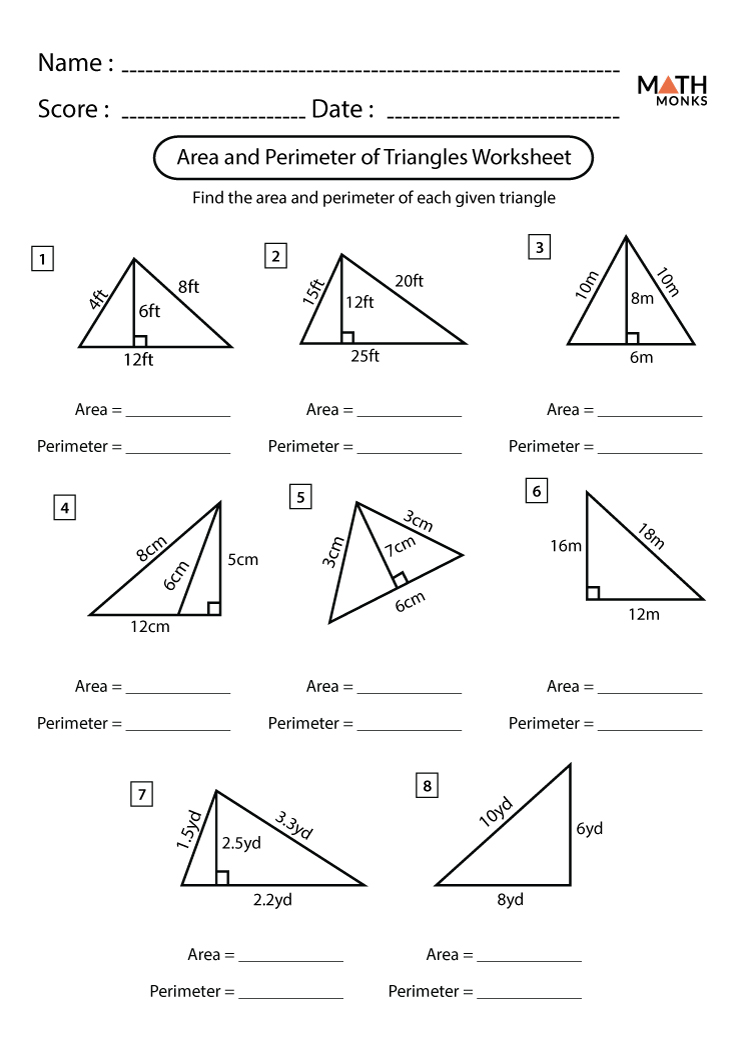
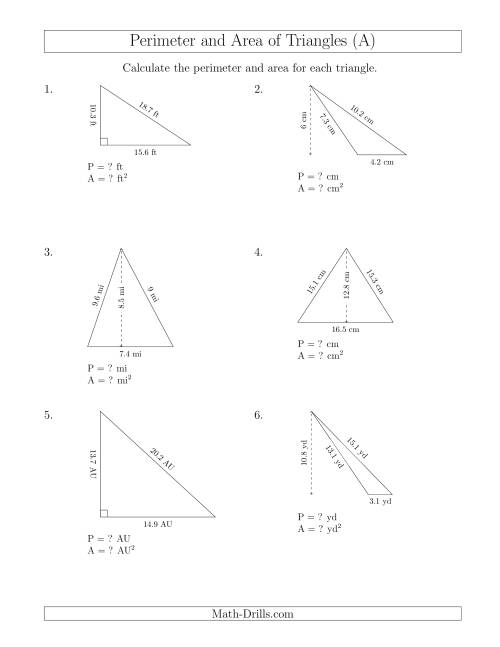
Topic right triangle perimeter: Explore the fascinating world of geometry with our comprehensive guide on calculating the perimeter of right triangles, an essential concept with practical applications in various fields, enriching your mathematical understanding and skills.
Table of Content
- How can I calculate the perimeter of a right triangle using the Pythagorean theorem?
- Definition and Basic Formula
- Pythagorean Theorem and Its Application
- Examples and Solutions
- YOUTUBE: Area and Perimeter of a Right Triangle
- Special Right Triangles: 30°-60°-90° and 45°-45°-90°
- Using Trigonometry: Law of Sines and Cosines
- Pythagorean Triples
- Common Mistakes and Tips
- Practical Applications in Real-Life Scenarios
- Frequently Asked Questions
How can I calculate the perimeter of a right triangle using the Pythagorean theorem?
To calculate the perimeter of a right triangle using the Pythagorean theorem, we need to follow these steps:
- Identify the lengths of the triangle\'s two legs (a and b) and the hypotenuse (c).
- Use the Pythagorean theorem: a^2 + b^2 = c^2
- Solve the equation to find the length of the hypotenuse (c).
- Once you know the lengths of the legs and the hypotenuse, you can calculate the perimeter by adding all three sides together: perimeter = a + b + c.
Let\'s consider an example:
| Leg a | Leg b | Hypotenuse c |
|---|---|---|
| 3 units | 4 units | ? |
Plug the values into the Pythagorean theorem:
- 3^2 + 4^2 = c^2
- 9 + 16 = c^2
- 25 = c^2
- c = √25
- c = 5 units
Finally, calculate the perimeter:
- perimeter = 3 + 4 + 5
- perimeter = 12 units
Therefore, the perimeter of a right triangle with legs of length 3 units and 4 units, and a hypotenuse of length 5 units, is 12 units.
READ MORE:
Definition and Basic Formula
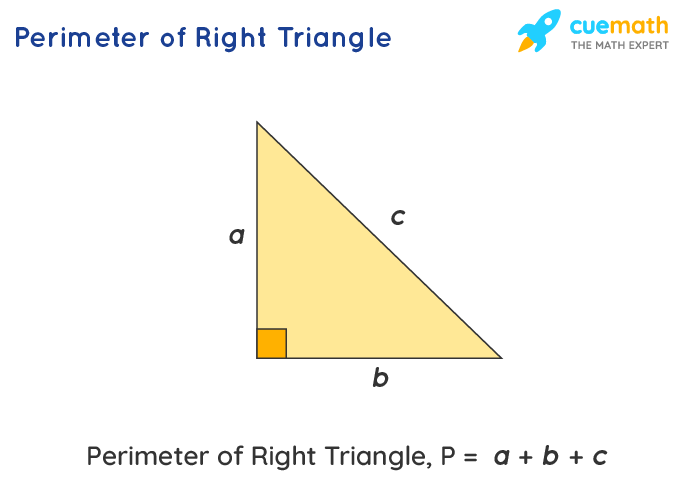
The perimeter of a right triangle is the sum of its three sides. The formula for the perimeter is P = a + b + c, where \"a\", \"b\", and \"c\" represent the lengths of the triangle\"s sides. In a right triangle, the sides \"a\" and \"b\" form the right angle, and \"c\" is the hypotenuse. The Pythagorean theorem, which states that c² = a² + b², plays a crucial role in calculating the perimeter, especially when one of the sides is unknown.
- To find the missing side \"a\", the formula is a = √(c² - b²).
- For the missing side \"b\", the formula is b = √(c² - a²).
- If \"c\" (the hypotenuse) is unknown, it can be calculated as c = √(a² + b²).
Once the lengths of all three sides are known, they can be added together to find the perimeter. If any side is missing, these formulas can be used to find the missing measurement before calculating the perimeter.
Alternate Formulas for Perimeter
- If the hypotenuse \"c\" is not known: Perimeter = a + b + √(a² + b²).
- When \"a\" is unknown: Perimeter = b + c + √(c² - b²).
- If \"b\" is missing: Perimeter = c + a + √(c² - a²).
Practical Examples
- For a triangle with base = 4 units, height = 12 units, and hypotenuse = 20 units, the perimeter is 36 units.
- In a triangle with base = 6 units and height = 8 units, first find the hypotenuse using the Pythagorean theorem (hypotenuse = √(6² + 8²) = 10 units) and then calculate the perimeter as 24 units.
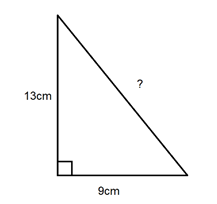
- For a triangle with base = 5 units and hypotenuse = 13 units, find the height using the Pythagorean theorem (height = √(13² - 5²) = 12 units) and calculate the perimeter as 30 units.

Pythagorean Theorem and Its Application
The Pythagorean Theorem is a fundamental principle in geometry, especially relevant for right triangles. It states that in any right triangle, the square of the length of the hypotenuse (c) is equal to the sum of the squares of the other two sides (a and b). This can be expressed as c² = a² + b². This theorem is not only a cornerstone of geometric theory but also a practical tool in various applications.
Application in Calculating Perimeter
The Pythagorean Theorem is particularly useful in calculating the perimeter of a right triangle when two sides are known. Once the lengths of all three sides are determined, the perimeter can be found by simply adding these lengths together. The perimeter formula for a right triangle is P = a + b + c.
- If only the lengths of the two legs (a and b) are known, the length of the hypotenuse (c) can be found using the theorem: c = √(a² + b²).
- Conversely, if one leg and the hypotenuse are known, the missing leg\"s length can be calculated.
Examples of Pythagorean Theorem Application
- For a right triangle with legs of 5m and 12m, the hypotenuse can be calculated as √(5² + 12²) = √(25 + 144) = √169 = 13m. The perimeter is then 5m + 12m + 13m = 30m.
- In another example, if a right triangle has a leg of 8m and a hypotenuse of 17m, the other leg can be calculated as √(17² - 8²) = √(289 - 64) = √225 = 15m. The perimeter in this case is 8m + 15m + 17m = 40m.
These applications demonstrate how the Pythagorean Theorem is essential for solving real-world problems involving right triangles, from basic geometry to more complex calculations in various fields.

Examples and Solutions
Understanding the perimeter of right triangles is enhanced by practical examples. These examples not only demonstrate the application of the Pythagorean theorem but also help in grasping the concept of perimeter in real-world scenarios.
Example 1: Basic Calculation
Consider a right triangle with sides of lengths 3 cm, 4 cm, and 5 cm. The perimeter is simply the sum of these lengths.
- Perimeter = 3 cm + 4 cm + 5 cm = 12 cm.
Example 2: Using Pythagorean Theorem
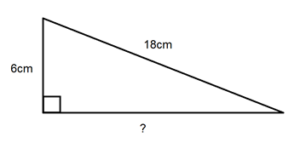
For a triangle with two known sides of 6 cm (base) and 8 cm (height), the hypotenuse (c) can be found using c² = a² + b²:
- c = √(6² + 8²) = √(36 + 64) = √100 = 10 cm.
- Perimeter = 6 cm + 8 cm + 10 cm = 24 cm.
Example 3: Unknown Leg Length
If a right triangle has a hypotenuse of 13 cm and one leg of 5 cm, the other leg (b) can be calculated as follows:
- b = √(13² - 5²) = √(169 - 25) = √144 = 12 cm.
- Perimeter = 5 cm + 12 cm + 13 cm = 30 cm.
Example 4: Application in Real Life
Consider a triangular field with one side of 50 meters and another side perpendicular to it measuring 120 meters. To find the fencing required around the field:
- First, calculate the hypotenuse: c = √(50² + 120²) = √(2500 + 14400) = √16900 = 130 meters.
- Then, calculate the perimeter: Perimeter = 50 m + 120 m + 130 m = 300 m.
These examples illustrate the practical utility of the Pythagorean theorem in determining the perimeter of right triangles, a skill useful in various academic and real-world applications.

Area and Perimeter of a Right Triangle
\"Discover the fascinating world of triangles and unlock their secrets in this captivating video! From the Pythagorean theorem to the angles and sides, prepare to be amazed by the versatility and beauty of this geometric shape.\"
Finding the Area and Perimeter of a Right Triangle
\"Unleash your mathematical prowess and delve into the realms of area and perimeter with this enlightening video! Learn how to calculate these fundamental concepts and explore their practical applications in real-world scenarios. Get ready to master the art of measurement!\"
Special Right Triangles: 30°-60°-90° and 45°-45°-90°
Special right triangles, specifically the 30°-60°-90° and 45°-45°-90° triangles, have unique properties that simplify the calculation of their perimeters. Understanding these properties allows for quick and efficient solutions to geometric problems involving these triangles.
30°-60°-90° Triangle
In a 30°-60°-90° right triangle, the sides are in a specific ratio relative to each other. If the shortest side (opposite the 30° angle) is \"a\", then:
- The side opposite the 60° angle is \"a√3\".
- The hypotenuse (opposite the 90° angle) is \"2a\".
Thus, the perimeter of a 30°-60°-90° triangle can be expressed as P = a + a√3 + 2a.
45°-45°-90° Triangle
The 45°-45°-90° triangle, also known as an isosceles right triangle, has two sides of equal length and the hypotenuse as the longest side. If each of the equal sides is \"b\", then:
- The hypotenuse can be calculated using the formula c = b√2 (since it\"s an isosceles right triangle).
Therefore, the perimeter of a 45°-45°-90° triangle is P = 2b + b√2.
Practical Examples
- 30°-60°-90° Example: If the shortest side (a) is 4 cm, the perimeter is P = 4 cm + 4√3 cm + 8 cm. Calculate the exact value or use a numerical approximation for √3.
- 45°-45°-90° Example: For a triangle with each of the equal sides (b) measuring 5 cm, the perimeter is P = 2(5 cm) + 5√2 cm. Again, calculate the exact value or use a numerical approximation for √2.
These special triangles are helpful in various geometric calculations and can simplify complex problems involving right triangles.
_HOOK_
Using Trigonometry: Law of Sines and Cosines
While the Pythagorean theorem is specific to right triangles, the Law of Sines and Cosines are powerful tools in trigonometry used to solve for missing sides and angles in any triangle, including right triangles. These laws are particularly useful when the standard formulas for right triangle calculations are not applicable.
Law of Sines
The Law of Sines states that the ratio of the length of a side of a triangle to the sine of its opposite angle is constant for all three sides and angles in the triangle. It is given as a/sin(A) = b/sin(B) = c/sin(C), where \"a\", \"b\", \"c\" are the sides, and \"A\", \"B\", \"C\" are the respective opposite angles.
Law of Cosines
The Law of Cosines is a generalized form of the Pythagorean theorem. It relates the lengths of the sides of a triangle to the cosine of one of its angles. It is particularly useful in finding a side when two sides and the included angle are known, or in finding an angle when all three sides are known. The formula is given by c² = a² + b² - 2ab*cos(C), where \"C\" is the angle opposite side \"c\".
Application in Right Triangles
- In a right triangle, if one angle and one side are known, the Law of Sines can be used to find another angle, and subsequently the missing sides.
- The Law of Cosines simplifies to the Pythagorean theorem in right triangles but can be used when only two sides and the non-right angle are known.
Practical Examples
- Using Law of Sines: If a triangle has sides a = 7, b = 9, and angle A = 30°, find angle B. Here, sin(B)/9 = sin(30°)/7. Calculating B gives the second angle, and subsequently, the third side can be calculated.
- Using Law of Cosines: For a triangle with sides a = 5, b = 6, and angle C = 60°, the length of side c can be found using c² = 5² + 6² - 2*5*6*cos(60°). Then, the perimeter can be calculated as the sum of the three sides.
These trigonometric laws expand the toolkit for solving various problems involving right triangles, making them indispensable in advanced geometry and applications.

Pythagorean Triples
Pythagorean triples are sets of three positive integers that form the sides of right triangles and satisfy the Pythagorean theorem, a² + b² = c², where \"c\" is the hypotenuse, and \"a\" and \"b\" are the other two sides. These triples are valuable in various mathematical and real-world applications due to their ability to easily identify the sides of right triangles.
Common Pythagorean Triples
- The most well-known triple is (3, 4, 5), where 3² + 4² = 5².
- Other examples include (5, 12, 13), (7, 24, 25), and (8, 15, 17).
These triples can be scaled up by multiplying each number in the triple by a common factor, and the resulting set will also form a Pythagorean triple.
Generating Pythagorean Triples
Pythagorean triples can be generated using formulas. For example, for any positive integers \"m\" and \"n\" (where m > n), the triple (m² - n², 2mn, m² + n²) forms a Pythagorean triple.
Application in Calculating Perimeter
Knowing a set of Pythagorean triples allows for quick calculation of the perimeter of right triangles:
- For a 3-4-5 triangle, the perimeter is 3 + 4 + 5 = 12 units.
- For a triangle with sides 5, 12, and 13, the perimeter is 5 + 12 + 13 = 30 units.
Pythagorean triples provide a simple and effective way to solve problems involving right triangles, making them an essential tool in geometry.
Common Mistakes and Tips
Calculating the perimeter of a right triangle can be tricky. A common mistake is incorrectly applying the Pythagorean theorem or misidentifying the sides of the triangle. Remember, the hypotenuse is always the longest side opposite the right angle.
Here are some tips to avoid errors:
- Double-check your calculations, especially when using the Pythagorean theorem.
- Ensure you correctly identify the base, height, and hypotenuse of the triangle.
- Remember that the perimeter is the sum of all three sides.
- Use appropriate formulas when a side is missing, such as a = sqrt(c^2 - b^2) if \"a\" is unknown.
- Practice with different examples to build confidence.
For example, in a triangle with a base of 6 units and height of 8 units, calculate the hypotenuse using c^2 = a^2 + b^2 before summing all sides for the perimeter.
Practical Applications in Real-Life Scenarios
Understanding the perimeter of right triangles is not only crucial in mathematical theory but also has diverse applications in real life. These applications range from navigation and construction to astronomy and various engineering fields. Here are some of the key areas where this knowledge is applied:
- Navigation: In navigation, especially in maritime and aviation industries, right triangles are used to calculate courses and bearings. The course of a ship or an aircraft is determined by the angle measured from a reference direction (usually north) to the line of travel. Bearings, on the other hand, are used to determine the direction from one point to another using right triangles.
- Construction: In construction, right triangles are employed to calculate the pitch of roofs. The pitch, which is a ratio of the rise to the span of the roof, can be determined by understanding the properties of right triangles. This knowledge is essential for architects and engineers to design and construct buildings and structures with the correct roof slopes.
- Height and Distance Measurement: The principles of right triangles are used to measure the height of tall objects, like buildings or trees, without the need for direct measurement. By measuring a known distance from the object and the angle of elevation to the top of the object, the height can be calculated using trigonometric functions.
- Physics and Engineering: In physics, right triangles are essential in breaking down forces into their components. This is crucial in fields like statics, dynamics, and kinematics. Engineers use these principles to design machines, structures, and analyze forces.
- Astronomy: Astronomers use right triangles to calculate the distance of stars and planets from Earth. By measuring angles from two different points on Earth and understanding the properties of right triangles, they can estimate the distance to these celestial bodies.
These examples illustrate the profound impact that a fundamental understanding of right triangles and their perimeters can have in various practical scenarios.
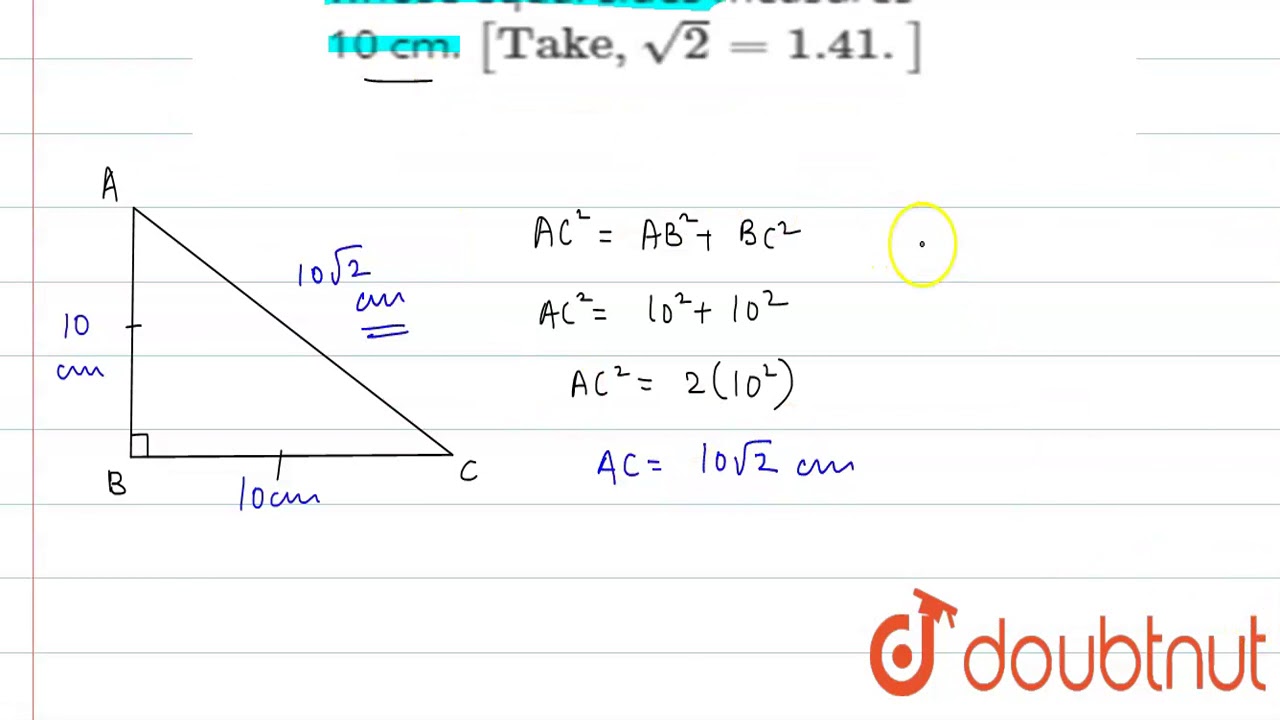
READ MORE:
Frequently Asked Questions
- What is the Perimeter of a Right-Angled Triangle?
- The perimeter of a right-angled triangle is the sum of the lengths of its three sides: base, height (altitude), and hypotenuse. It is calculated using the formula: Perimeter = base + height + hypotenuse.
- How Do You Calculate the Perimeter if One Side is Missing?
- If one side of a right-angled triangle is missing, you can use the Pythagorean theorem (c² = a² + b²) to find the missing length. Once you have all three side lengths, add them together to get the perimeter.
- What is the Pythagorean Theorem?
- The Pythagorean theorem states that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. The formula is c² = a² + b².
- Is the Perimeter the Same as the Area of a Triangle?
- No, the perimeter and the area of a triangle are different. The perimeter is the total length of the boundary, while the area is the amount of space enclosed within the triangle.
- How Do You Find the Perimeter of a Right Triangle with Unequal Sides?
- If the sides are unequal, add the lengths of all three sides to find the perimeter. For a right-angled triangle, if the lengths are a, b, and c, the perimeter is a + b + c.
- Can the Perimeter of a Right Triangle be the Same as an Equilateral Triangle?
- Yes, it\"s possible for a right triangle and an equilateral triangle to have the same perimeter if the sum of the lengths of their sides is equal.
- What are Some Real-World Applications of Calculating the Perimeter of Right Triangles?
- Calculating the perimeter of right triangles is used in various fields such as architecture, construction, and engineering for measuring and planning purposes.
- What is a Semiperimeter?
- The semiperimeter of a triangle is half of its perimeter. It\"s used in various geometric calculations and formulas.
- If One Side of a Right Triangle is 12, What Could be the Greatest Possible Perimeter?
- The greatest possible perimeter occurs with a triangle whose sides are 12, 35, and 37 units, resulting in a perimeter of 84 units.
Embark on a journey of geometric discovery! This comprehensive guide to right triangle perimeters offers practical insights, useful formulas, and intriguing applications. Perfect for learners and enthusiasts, it turns complex concepts into accessible knowledge, enhancing your mathematical journey.

_HOOK_