Formula for Perimeter of Right Triangle: Unlocking Geometry"s Secrets

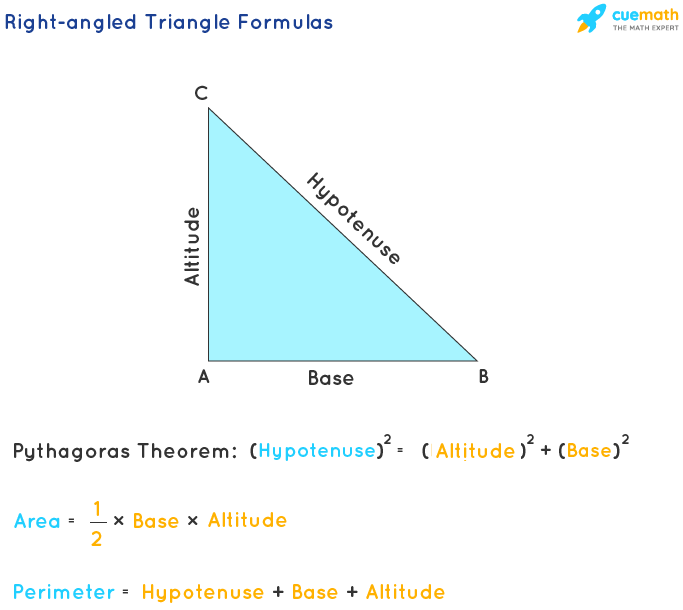
A right triangle, a fundamental shape in geometry, has one angle exactly 90 degrees, making it unique. It consists of three sides: the hypotenuse (the longest side), the base, and the height (or perpendicular). The unique properties of right triangles are the cornerstone of trigonometry and many real-world applications.

• Angles: Besides the right angle, the other two angles of a right triangle must sum up to 90 degrees, as the total sum of angles in any triangle is 180 degrees.
• Sides: The sides of a right triangle are interconnected. The hypotenuse is always opposite the right angle and is the longest side. The other two sides are adjacent to the right angle.
• Pythagorean Theorem: This theorem is a fundamental element in understanding right triangles. It states that the square of the hypotenuse\"s length is equal to the sum of the squares of the other two sides.

Identifying and understanding these elements are crucial in solving problems related to right triangles, including finding their perimeter.

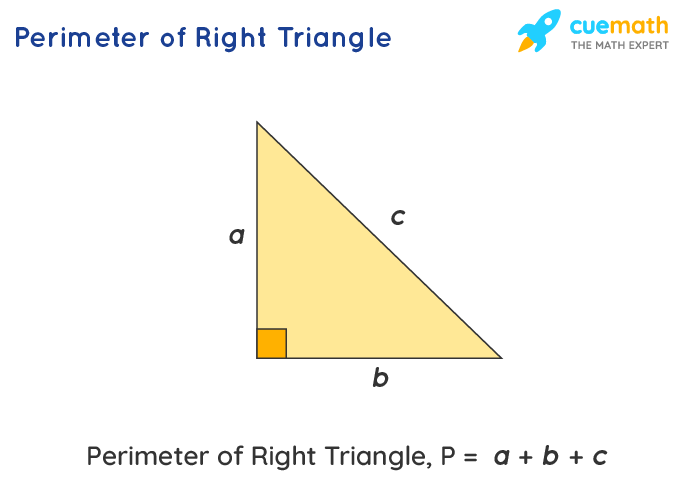
The perimeter of a right triangle is the total length of its three sides. It\"s calculated by simply adding the lengths of the hypotenuse, base, and height. This basic formula is fundamental in various geometry applications.

1. Determining the Sides: Measure or calculate the lengths of the three sides of the right triangle - the hypotenuse, base, and height.
2. Applying the Formula: Use the formula Perimeter = Hypotenuse + Base + Height. This formula is derived from the general triangle perimeter formula, which sums the lengths of all sides.

Remember, the accuracy of the perimeter calculation hinges on the precise measurement or calculation of the triangle\"s sides. This basic understanding is pivotal in solving more complex geometric problems.

The Pythagoras Theorem is a pivotal concept in calculating the perimeter of a right triangle when not all side lengths are known. It states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.

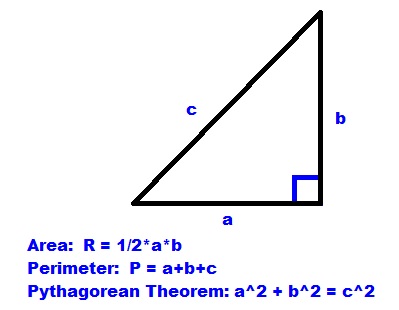
1. Formula of Pythagoras Theorem: It is expressed as c² = a² + b², where \"c\" is the hypotenuse and \"a\" and \"b\" are the other two sides.
2. Finding the Missing Side: If one side of a right triangle is unknown, you can rearrange the Pythagoras equation to find it. For example, if \"a\" is unknown, then a = √(c² - b²).
3. Calculating the Perimeter: Once all sides are known, add them to find the perimeter using the formula Perimeter = a + b + c.

This method is especially useful in real-world applications where measuring all sides directly might not be feasible, and only two sides are known.

The Leg Rule is a specialized method used in calculating the perimeter of a right triangle, particularly useful when the lengths of the legs are not directly known but can be deduced from other information. It relates the legs of a right triangle to segments projected on the hypotenuse.

1. Understanding the Leg Rule: This rule states that each leg of a right triangle is the geometric mean between the length of the hypotenuse and the length of the projection of that leg on the hypotenuse.
2. Application in Perimeter Calculation: To use the Leg Rule for finding a triangle\"s perimeter, one must first calculate the lengths of the legs if they are unknown. This can be done by using the formulae derived from the Leg Rule, which require knowing the hypotenuse and the projections of the legs on it.
3. Calculating the Perimeter: Once the lengths of the legs are known, along with the length of the hypotenuse, the perimeter of the right triangle can be calculated by adding these three sides.

This approach is particularly advantageous when direct measurement of the legs is not possible but their projections on the hypotenuse are known or can be calculated.

In the realm of right triangles, isosceles and scalene right triangles present unique cases. Understanding their properties is crucial for accurate perimeter calculations.

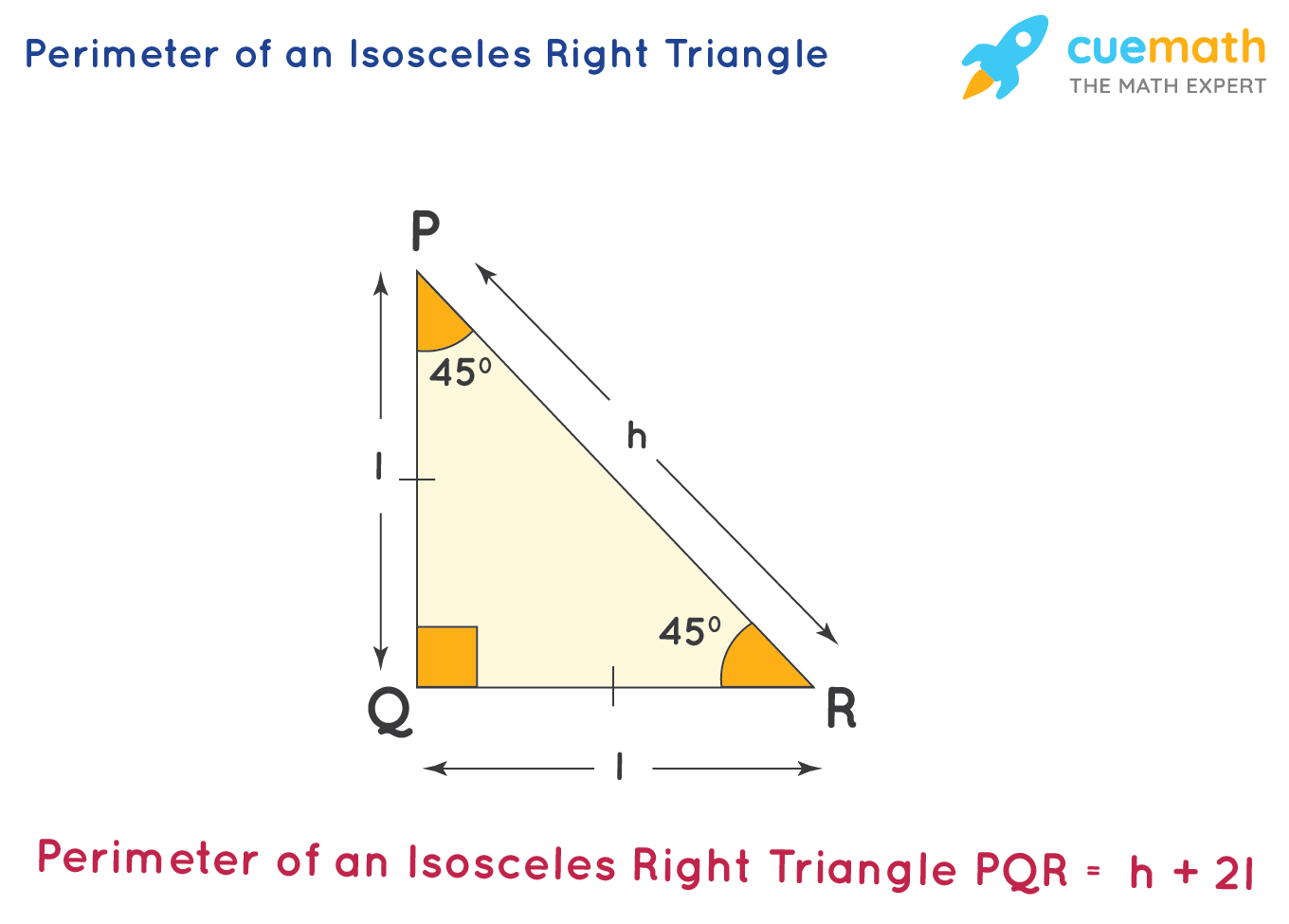
Isosceles Right Triangle

• An isosceles right triangle has two sides of equal length, known as the legs, and a hypotenuse opposite the right angle.
• The two equal angles are each 45 degrees.
• The formula for the hypotenuse in such triangles is ( h = sqrt{2} imes ext{side length} ).
• Perimeter can be calculated using the formula ( P = 2 imes ext{side length} + ext{hypotenuse} ).

Scalene Right Triangle

• In a scalene right triangle, all three sides are of different lengths.
• Perimeter calculation remains the standard ( P = a + b + c ), where ( a, b, ) and ( c ) are the side lengths.
• For missing side lengths, the Pythagorean theorem or trigonometric laws (like the Law of Cosines or Sines) can be applied.
• The Law of Cosines, for instance, is used when one side is unknown, and is given by ( c = sqrt{a^2 + b^2 - 2ab cos(gamma)} ), where ( gamma ) is the angle opposite to the unknown side.

Both isosceles and scalene right triangles offer interesting variations in right triangle geometry, each requiring a tailored approach for perimeter calculations.

When calculating the perimeter of right triangles, the Law of Cosines and the Law of Sines are powerful tools, especially when specific sides or angles are unknown. These laws extend the basic Pythagorean theorem to more complex triangle configurations.

Law of Cosines

• Useful for calculating the length of one side when you know the lengths of two sides and the included angle.
• The formula is ( c^2 = a^2 + b^2 - 2abcos(gamma) ) where ( a, b, ) and ( c ) are the sides of the triangle and ( gamma ) is the included angle.
• For perimeter calculation, once all sides are known, sum them up.

Law of Sines

• Applicable when two angles and one side are known, or when two sides and a non-included angle are known.
• The formula is ( frac{a}{sin(A)} = frac{b}{sin(B)} = frac{c}{sin(C)} ), relating the sides of a triangle to the sines of their respective angles.
• It allows for the calculation of unknown sides, which are then added for the perimeter.

Both these laws are essential for solving various triangle problems, not just for right triangles but for any triangle, providing a comprehensive approach to understanding and solving geometry problems.

Example 1: Basic Right Triangle Perimeter Calculation

Find the perimeter of a right-angled triangle with a base of 4 units, height of 12 units, and hypotenuse of 20 units.

Solution: Given, base = 4 units, height = 12 units, hypotenuse = 20 units. Thus, the perimeter = base + height + hypotenuse = 4 + 12 + 20 = 36 units.

Example 2: Using Pythagoras Theorem

For a right-angled triangle with a base of 6 units and height of 8 units, find its perimeter.

Solution: Given, base = 6 units, height = 8 units. To find the hypotenuse, use the Pythagoras theorem: (Hypotenuse)^2 = (Base)^2 + (Height)^2, which gives Hypotenuse = √100 = 10 units. Therefore, the perimeter = 6 + 8 + 10 = 24 units.

Example 3: Finding a Missing Side

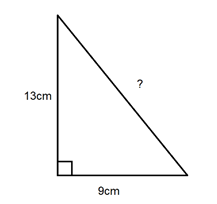
Calculate the perimeter of a right triangle if the base is 5 units and the hypotenuse is 13 units.

Solution: Base = 5 units, Hypotenuse = 13 units. To find the height, apply Pythagoras theorem: (Hypotenuse)^2 = (Base)^2 + (Height)^2. This gives us Height = 12 units. So, the perimeter = 5 + 13 + 12 = 30 units.

Additional Practice Questions

1. Find the perimeter of a right triangle with a base of 6 units and a height of 8 units.
2. Calculate the cost of fencing a right triangle with a base of 3 meters and height of 4 meters, if the cost of fencing is $20/m.
3. What is the perimeter of a right triangle with a base of 14 m and a height of 48 m?
4. If the area of a right triangle is 24 cm² and height is 8 cm, find its perimeter.
5. If the height and base of a right triangle are both \"l\" cm long, what is its perimeter?

Common Mistakes

• Confusing Perimeter with Area: Students often mix up the concepts of perimeter and area. While perimeter is the sum of the lengths of all sides of a triangle, area is the space enclosed within it.
• Miscalculating the Hypotenuse: Forgetting to apply the Pythagorean theorem correctly when one or more sides of the right triangle are unknown is a common error.
• Unit Inconsistency: Adding side lengths that are not in the same unit can lead to incorrect perimeter calculations.
• Order of Addition: Some students mistakenly believe that the order in which the sides are added affects the outcome. The commutative property of addition assures that the order does not matter.

Teaching Tips

• Varying Question Types: Use worksheets with different types of triangles (isosceles, equilateral, scalene, right-angled) and questions (calculating perimeter, finding missing sides, word problems).
• Real-World Applications: Engage students with practical applications, such as measuring and calculating the perimeter of real objects.
• Visual Learning: Utilize visual aids and geometric tools to help students understand and apply the Pythagorean theorem and perimeter calculations.
• Emphasize Units: Teach the importance of unit consistency and conversion in calculations.

Right triangles are extensively used in various fields due to their unique properties. Understanding the perimeter of right triangles is particularly important in real-world applications. Here are some examples:

Engineering

In engineering, right triangles are essential for calculating forces, stability, and analyzing structural elements. They are also used in electrical engineering for calculations related to circuit design.

Physics

In physics, right triangles aid in resolving forces into components, and are used in mechanics, motion, and trigonometric calculations related to waves and circular motion.

Surveying and Navigation

Right triangles play a significant role in surveying and navigation, particularly in triangulation methods used for determining distances, angles, and positions on the Earth\"s surface.

Architecture and Construction

Architectural design and construction heavily rely on right triangles for various calculations and structural designs.

Computer Graphics and Surveying

Right triangles are also fundamental in computer graphics, aiding in rendering 3D objects, and in surveying for land measurements and mapping.

These applications show how the principles of right triangles and their perimeters are embedded in many aspects of our daily life and professional fields.

Unveiling the secrets of right triangles, this comprehensive guide illuminates their perimeters\" calculation and real-world applications, beckoning readers to explore the fascinating world of geometry and its practical significance in various fields.