Topic how to find perimeter of a right triangle: Discover the simple yet intriguing process of finding the perimeter of a right triangle, a fundamental concept in geometry that opens the door to a world of mathematical understanding and practical applications.
Table of Content
- Understanding the Perimeter of a Right Triangle
- YOUTUBE: Area and Perimeter of a Right Triangle | Math with Mr. J
- Basic Formula for Calculating Perimeter
- Using the Pythagorean Theorem
- Special Cases: Known Side Lengths
- Applying the Law of Cosines and Sines
- Examples and Solutions
- Practical Applications and Real-World Examples
- Common Mistakes and How to Avoid Them
- FAQs and Additional Resources
Understanding the Perimeter of a Right Triangle
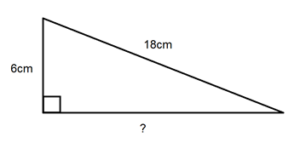
The perimeter of a right triangle is the total distance around its three sides. It is calculated by summing the lengths of these sides, typically designated as \"a\", \"b\", and \"c\". In right triangles, sides \"a\" and \"b\" form the 90-degree angle, while \"c\" represents the hypotenuse.
Calculating the perimeter involves using the fundamental formula: Perimeter = a + b + c. However, in some cases, not all side lengths are known. The Pythagorean Theorem can be employed in these situations to find the missing side lengths. This theorem states that in a right triangle, the square of the hypotenuse (c) is equal to the sum of the squares of the other two sides (a and b), formulated as c² = a² + b².
- If the lengths of \"a\" and \"b\" are known, the length of \"c\" can be calculated as c = √(a² + b²).
- If \"a\" and \"c\" are known, then b can be determined using b = √(c² - a²).
- If \"b\" and \"c\" are known, a is found by a = √(c² - b²).
Once all side lengths are determined, the perimeter is easily calculated. Here are some examples:
- If a right triangle has sides of 4, 12, and 20 units, its perimeter is 4 + 12 + 20 = 36 units.
- For a triangle with a base of 6 units and a height of 8 units, the hypotenuse is 10 units, leading to a perimeter of 24 units.
- A triangle with a base of 5 units and a hypotenuse of 13 units will have a height of 12 units and a perimeter of 30 units.
Understanding these principles and formulas helps accurately determine the perimeter of right triangles, essential in various mathematical and real-world applications.

READ MORE:
Area and Perimeter of a Right Triangle | Math with Mr. J
Get ready to dive into the fascinating world of geometry as we explore the concept of perimeter in this captivating video. Discover how to calculate the perimeter of various shapes and unlock the secrets to finding the perfect balance between length and width. Join us on this mathematical journey and expand your understanding of perimeter in a visually engaging and informative way!
Elegant way to find the Perimeter of a right triangle | step-by-step explanation | math
Prepare to be mesmerized by the beauty of elegance in this enchanting video. Experience the graceful movements and sophisticated designs, as we delve into the essence of elegance across various domains. From elegant fashion and stunning architecture to refined dance forms and sophisticated cuisine, this video will leave you inspired by the timeless allure of elegance in all its forms.
Basic Formula for Calculating Perimeter
The basic formula for calculating the perimeter of a right triangle is straightforward: it involves the sum of the lengths of all three sides of the triangle. In mathematical terms, if \"a\", \"b\", and \"c\" represent the lengths of the sides, with \"c\" typically being the hypotenuse, the perimeter (P) is calculated as P = a + b + c.
However, there are instances where you might not know the lengths of all three sides. In such cases, the Pythagorean theorem becomes essential. This theorem states that in a right triangle, the square of the hypotenuse (c) is equal to the sum of the squares of the other two sides (a and b). It can be expressed as c² = a² + b².
Using the Pythagorean theorem, if you know two sides of the triangle, you can find the third side and then compute the perimeter:
- If \"a\" and \"b\" are known, calculate \"c\" as c = √(a² + b²).
- If \"a\" and \"c\" are known, find \"b\" using b = √(c² - a²).
- If \"b\" and \"c\" are known, \"a\" is determined by a = √(c² - b²).
Once all sides are known, add them together to find the perimeter. This formula is pivotal in many practical applications, such as construction, crafting, and geometry problems.

Calculate side lengths of the right triangle | Area and Perimeter are known | Geometry Olympiad
Uncover the hidden wonders behind the world of side lengths in this eye-opening video. Explore how the length of each side can dramatically influence the shape and properties of objects in our everyday lives. From determining the lengths of triangle sides to unraveling the mysteries of complex polygons, this video will redefine your perception of side lengths and empower you with the knowledge to analyze shapes with precision and finesse.
Using the Pythagorean Theorem
The Pythagorean Theorem is a fundamental tool in geometry, especially for calculating the perimeter of a right triangle. This theorem states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. The formula is expressed as a² + b² = c², where \"a\" and \"b\" are the lengths of the two legs and \"c\" is the length of the hypotenuse.
To use the Pythagorean Theorem for finding a right triangle\"s perimeter:
- Identify the lengths of any two sides of the triangle.
- Apply the Pythagorean Theorem to find the length of the third side.
- Once all side lengths are known, add them together to get the perimeter (P = a + b + c).
For instance, if you know the lengths of the two legs (a and b), you can find the length of the hypotenuse (c) using the formula c = √(a² + b²). Similarly, if the hypotenuse and one leg are known, you can find the other leg by rearranging the formula: a = √(c² - b²) or b = √(c² - a²).
Examples:
- If the legs of a right triangle are 3 inches and 4 inches, then the hypotenuse is √(3² + 4²) = √(9 + 16) = √25 = 5 inches. Thus, the perimeter is 3 + 4 + 5 = 12 inches.
- For a right triangle with a hypotenuse of 15 inches and one leg of 9 inches, the other leg can be found as √(15² - 9²) = √(225 - 81) = √144 = 12 inches. Hence, the perimeter is 9 + 15 + 12 = 36 inches.
This theorem is a versatile tool in geometry, allowing the calculation of the third side of a right triangle when any two sides are known, thus facilitating the determination of the triangle\"s perimeter.

Special Cases: Known Side Lengths
In certain scenarios, we may already know some side lengths of a right triangle, which simplifies the process of finding its perimeter. The perimeter (P) of a right triangle is the sum of its three sides: P = a + b + c, where \"a\" and \"b\" are the legs and \"c\" is the hypotenuse.
Here are some special cases:
- If the lengths of both legs (a and b) are known, the hypotenuse (c) can be found using the Pythagorean theorem: c = √(a² + b²). The perimeter is then calculated as a + b + c.
- In cases where one leg and the hypotenuse are known (a and c, or b and c), the missing leg (b or a) can be determined using rearranged Pythagorean formulas: b = √(c² - a²) or a = √(c² - b²). Again, the perimeter is the sum of all three sides.
- Direct formulas can also be applied based on which sides are known. For instance, if \"a\" and \"b\" are known but \"c\" is not, the perimeter can be directly calculated as P = a + b + √(a² + b²).
Examples:
- For a triangle with known legs of 6 units and 8 units, first find the hypotenuse: √(6² + 8²) = √(36 + 64) = √100 = 10 units. The perimeter is 6 + 8 + 10 = 24 units.
- In a case with a known base of 5 units and a hypotenuse of 13 units, calculate the height using the formula: √(13² - 5²) = √(169 - 25) = √144 = 12 units. Therefore, the perimeter is 5 + 13 + 12 = 30 units.
These methods allow for efficient calculation of the perimeter in right triangles when certain side lengths are already known.
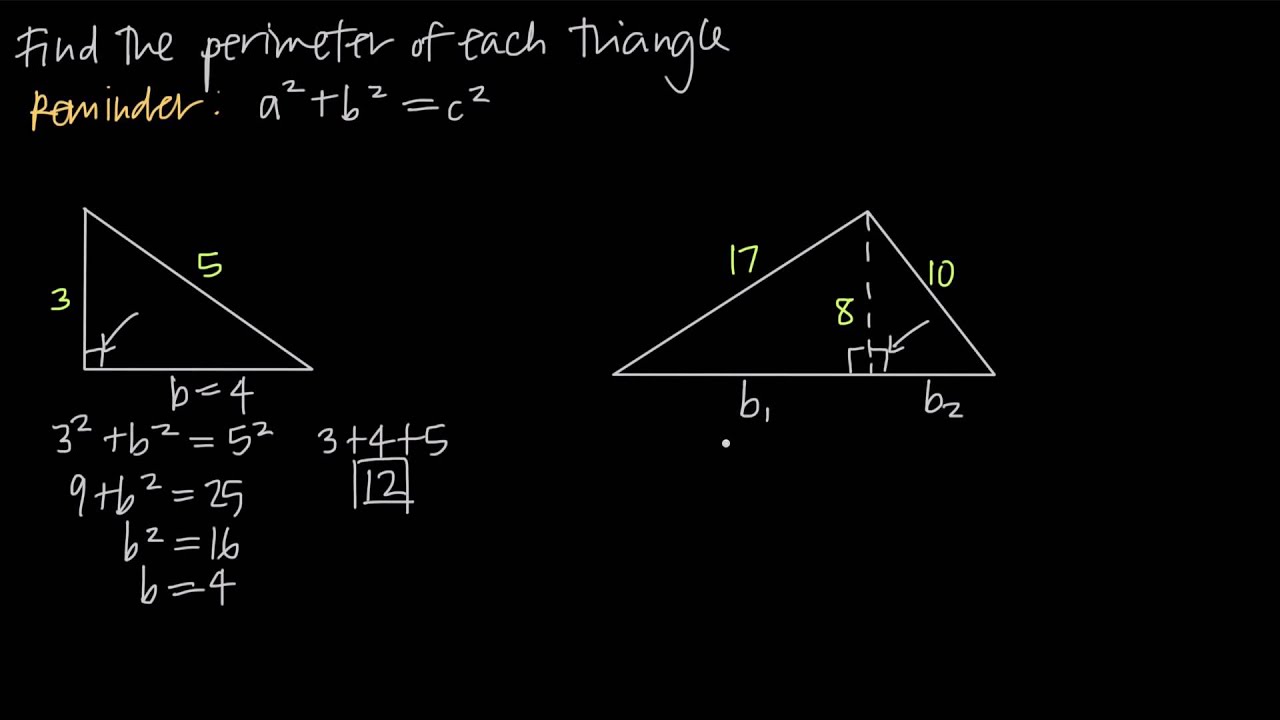
Applying the Law of Cosines and Sines
The Law of Cosines and Sines are crucial in finding the perimeter of a right triangle, especially in cases involving two known sides and an included angle (SAS) or two angles and a side (ASA). These laws provide a way to determine the unknown sides, which are then used to calculate the perimeter.
Using the Law of Cosines
The Law of Cosines is particularly useful when we have two sides and the included angle (SAS). It is given by the formula:
c² = a² + b² - 2ab * cos(γ),
where \"c\" is the side opposite the angle γ, and \"a\" and \"b\" are the other two sides. Once \"c\" is found, the perimeter can be calculated as P = a + b + c.
Using the Law of Sines
The Law of Sines is useful when two angles and a side (ASA) are known. It is expressed as:
a/sin(A) = b/sin(B) = c/sin(C),
where \"a\", \"b\", and \"c\" are sides of the triangle, and A, B, C are the opposite angles. With one side known, the other sides can be calculated using this formula, leading to the determination of the perimeter.
Examples:
- In a SAS scenario, if a = 10, b = 15, and angle γ = 30°, apply the Law of Cosines to find side c, then sum a, b, and c for the perimeter.
- For an ASA situation, suppose angle A = 40°, angle B = 70°, and side a = 8. Using the Law of Sines, find sides b and c, then calculate the perimeter.
These laws are essential in situations where the Pythagorean Theorem cannot be applied directly, such as non-right triangles or right triangles with unknown side lengths.
_HOOK_
Examples and Solutions
Understanding the perimeter of a right triangle can be enhanced by going through specific examples and their solutions. Below are some examples to illustrate this:
Example 1
Find the perimeter of a right-angled triangle with a base of 4 units, a height of 12 units, and a hypotenuse of 20 units.
Solution: The perimeter is the sum of all sides, so P = 4 + 12 + 20 = 36 units.
Example 2
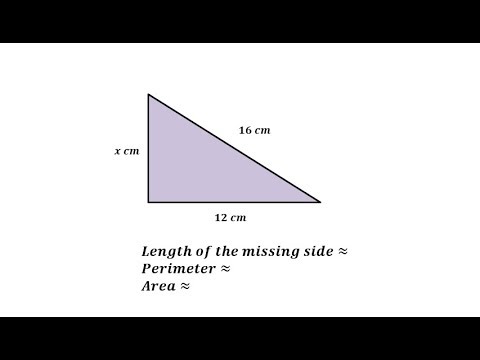
Calculate the perimeter of a right-angled triangle with a base of 6 units and a height of 8 units.
Solution: First, find the hypotenuse using the Pythagorean theorem: Hypotenuse = √(6² + 8²) = √(36 + 64) = 10 units. Then, the perimeter is 8 + 6 + 10 = 24 units.
Example 3
Determine the perimeter of a right triangle with a base of 5 units and a hypotenuse of 13 units.
Solution: Calculate the height using the Pythagorean theorem: Height = √(13² - 5²) = √(169 - 25) = 12 units. Therefore, the perimeter is 5 + 13 + 12 = 30 units.
Example 4
What is the perimeter of a right triangle with sides 5 m and 12 m?
Solution: Use the Pythagorean theorem to find the third side: c = √(5² + 12²) = 13 m. The perimeter is then 5 + 12 + 13 = 30 m.
Example 5
A right triangle has sides of lengths 8 m and 11 m. Calculate its perimeter.
Solution: First, find the length of the hypotenuse: c = √(8² + 11²) = 13.6 m. The perimeter is 8 + 11 + 13.6 = 32.6 m.
These examples provide a practical approach to understanding the calculation of the perimeter in various right triangle scenarios.
Practical Applications and Real-World Examples
Understanding the perimeter of a right triangle is not just a mathematical exercise; it has several practical applications in real life. Here are some examples:
Garden and Landscaping
One of the most common uses is in garden design and landscaping. If you\"re planning a triangular garden bed or a triangular section of your yard, knowing how to calculate the perimeter can help you estimate the amount of fencing or edging material needed. For example, if you know two sides of the triangular garden and the angle between them, you can use the law of cosines to find the third side and then calculate the perimeter.
Construction and Carpentry
In construction and carpentry, the perimeter of right triangles is crucial for creating accurate structures. Whether it\"s framing a triangular window or building a sloped roof, knowing the perimeter allows for precise material estimates and cuts.
Interior Decoration
For interior decoration, especially for creating triangular shelves or partitions, calculating the perimeter helps in determining the amount of trim or border materials needed.
Educational Tools
Teachers and educators can use the concept of finding the perimeter of right triangles to create interactive learning experiences for students, making geometry more engaging and practical.
Art and Craft Projects
In art and craft, especially in projects involving geometric shapes, calculating the perimeter of right triangles can assist in planning the layout and quantity of materials required.
These real-world applications demonstrate the importance and utility of understanding how to find the perimeter of right triangles in everyday life and various professional fields.

Common Mistakes and How to Avoid Them
When calculating the perimeter of a right triangle, several common errors can occur. Understanding and avoiding these mistakes is crucial for accurate results.
Mistake 1: Misunderstanding the Perimeter Formula
The perimeter of a right triangle is the sum of all its sides. A common mistake is confusing this with the area formula. Remember, the perimeter is simply the addition of the lengths of the three sides, including the hypotenuse, base, and height.
Mistake 2: Incorrect Application of the Pythagorean Theorem
When a side length is unknown, the Pythagorean theorem is used. However, errors can occur if it\"s applied incorrectly. Ensure that you correctly identify the hypotenuse (the longest side opposite the right angle) and the other two sides. The theorem states that the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Mistake 3: Confusing Different Types of Triangles
Different types of triangles, like equilateral or isosceles, have unique properties. For a right triangle, don\"t assume all sides are equal or two sides are equal unless it\"s specified (as in the case of an isosceles right triangle).
Mistake 4: Adding Sides with Different Units
Ensure all side lengths are in the same unit before adding. Convert any differing units to a common unit to avoid errors in calculation.
Mistake 5: Order of Addition
While the order of adding the sides doesn\"t impact the result due to the commutative property of addition, ensuring that each side is added only once is essential.
Additional Tips:
- Always double-check your calculations, especially when applying the Pythagorean theorem.
- Use diagrams where possible to visualize the problem and identify sides correctly.
- Practice with a variety of right triangle problems to become familiar with different scenarios.
By understanding these common mistakes and applying these tips, you can more accurately calculate the perimeter of right triangles.
READ MORE:
FAQs and Additional Resources
Understanding the perimeter of a right triangle involves knowing the basic concepts and formulas. Here are some frequently asked questions (FAQs) and additional resources to help deepen your knowledge and understanding.
FAQs on the Perimeter of a Right Triangle
- What is the Perimeter of a Right Triangle?
- The perimeter of a right triangle is the sum of its three sides: the base, the height (or altitude), and the hypotenuse.
- How is the Pythagorean Theorem Used in Right Triangles?
- The Pythagorean Theorem states that in a right triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. This is crucial for finding missing side lengths.
- What\"s the Difference Between Area and Perimeter of a Right Triangle?
- The area of a right triangle measures the space inside it and is calculated as half the product of its base and height. The perimeter is the total length of the triangle\"s sides.
- What\"s the Formula for the Perimeter of a Right Triangle?
- The formula is the sum of its three sides, often represented as P = a + b + c, where a, b, and c are the triangle\"s side lengths.
- How Do You Find the Area and Perimeter of a Triangle?
- For the area, use the formula: Area = ½ × base × height. The perimeter is found by adding the lengths of all three sides.
- What is the Greatest Possible Perimeter of a Right Triangle if One of the Sides is 12?
- The greatest possible perimeter of such a triangle would be 84, with the sides measuring 12, 35, and 37.
Additional Resources
- For more examples and detailed explanations, visit Cuemath and SplashLearn.
- Explore various types of triangles and their properties at Tutors.com and Third Space Learning.
- Engage with interactive quizzes and visual aids to strengthen your understanding of the concepts.
These resources provide a comprehensive understanding of the perimeter of right triangles, along with various examples and practice problems to enhance learning.
Mastering the perimeter of a right triangle opens a world of geometry understanding. This guide provides all you need to confidently calculate and apply this fundamental concept in varied scenarios, enhancing your mathematical journey.