Topic how to find the area and perimeter of a triangle: Unlock the secrets of triangles with this engaging guide on how to find their area and perimeter. Perfect for students, hobbyists, and geometry enthusiasts, this article simplifies these concepts with clear explanations and practical examples.
Table of Content
- Basics of Triangle Perimeter
- YOUTUBE: Finding Area and Perimeter of a Triangle
- Calculating Perimeter for Different Types of Triangles
- Introduction to Triangle Area
- Area Calculation Methods
- Special Formulas and Cases
- Practical Examples and Solved Problems
- Interactive Practice Problems
- Application in Real-World Scenarios
- Advanced Concepts and Theorems
- Summary and Key Takeaways
Basics of Triangle Perimeter
Understanding the perimeter of a triangle is crucial in geometry. Perimeter, derived from Greek words meaning \"around measure,\" is the sum of the lengths of a shape\"s boundary. For triangles, this means adding the lengths of all three sides.
The perimeter formula for a triangle is simple: ( P = a + b + c ) units, where ( a ), ( b ), and ( c ) are the lengths of the triangle\"s sides. This formula applies to all types of triangles, whether equilateral, isosceles, or scalene.
- Equilateral Triangle: With all sides equal, the perimeter is ( P = 3a ) units.
- Isosceles Triangle: Here, two sides are equal. The perimeter formula becomes ( P = 2a + b ) units.
- Scalene Triangle: This triangle has all sides of different lengths, and the perimeter is the sum of these three distinct lengths.
Real-world examples of calculating perimeter include tasks like determining the fencing required for a triangular garden or the lace needed to decorate the borders of a triangular serving tray. These practical applications highlight the importance of understanding how to calculate a triangle\"s perimeter accurately.

READ MORE:
Finding Area and Perimeter of a Triangle
Explore the mysterious world of triangles in this captivating video! Discover the secrets behind their unique properties and learn how to calculate their angles with simple yet fascinating explanations.
Calculating Triangle Area
Unlock the power of calculating in this mind-boggling video! Discover the tricks and techniques to solve complex equations and unleash your mathematical abilities like never before.
Calculating Perimeter for Different Types of Triangles
Calculating the perimeter of a triangle depends on its type: equilateral, isosceles, or scalene. The perimeter is the sum of the lengths of its sides.
Perimeter of an Equilateral Triangle
In an equilateral triangle, all sides are of equal length. The formula for its perimeter is simply:
( P = 3 imes a )
where ( a ) is the length of each side.
Perimeter of an Isosceles Triangle
An isosceles triangle has two equal sides. Its perimeter formula is:
( P = 2a + b )
where ( a ) is the length of the equal sides and ( b ) is the base.
Perimeter of Scalene Triangle
A scalene triangle has all sides of different lengths. The perimeter formula is:
( P = a + b + c )
where ( a ), ( b ), and ( c ) are the lengths of the three sides.
Understanding these formulas and applying them correctly is essential for accurately determining the perimeter of triangles in various contexts, such as in geometry problems or real-life applications like planning fencing around a triangular area.
Triangular Area and Perimeter on a Coordinate Plane
Dive into the enchanting realm of the coordinate plane with this mesmerizing video! Learn how to plot points, navigate through the grid, and bring mathematical concepts to life in a visually stunning way.
Introduction to Triangle Area
The area of a triangle is a measure of the space within its three sides. This concept is vital in geometry and has various practical applications. Understanding how to calculate the area of a triangle involves several formulas, depending on the information available.
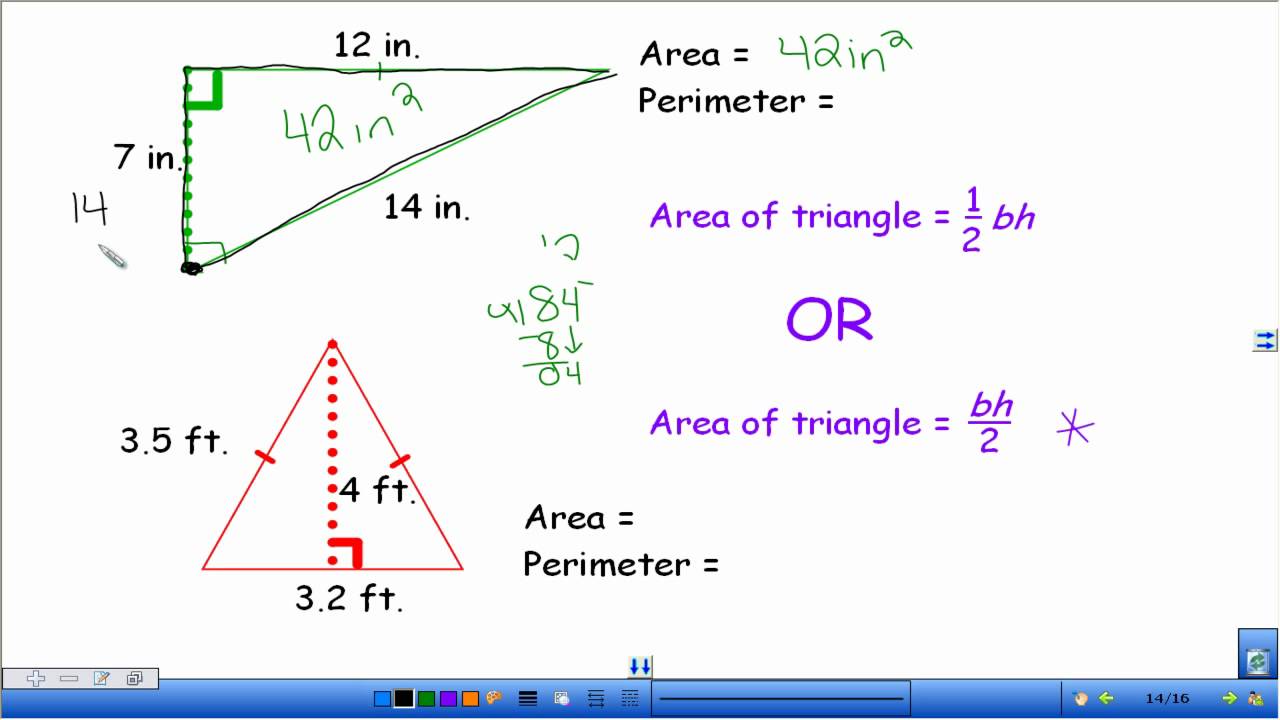
- The most basic formula for calculating the area of a triangle is ( A = frac{1}{2} imes ext{base} imes ext{height} ). In this formula, the base can be any side of the triangle, and the height is the perpendicular distance from the base to the opposite vertex.
- For triangles with known side lengths (a, b, c), Heron\"s formula is used. First, compute the semi-perimeter (s) as ( s = frac{a + b + c}{2} ). Then, the area is given by ( A = sqrt{s(s - a)(s - b)(s - c)} ).
- In the case of an equilateral triangle with side length \"a\", the area can be calculated using ( A = frac{sqrt{3}}{4} imes a^2 ).
- If two sides and the included angle (C) are known, the area is found using ( A = frac{1}{2} ab sin C ).
These formulas cater to different types of triangles, such as equilateral, isosceles, and scalene, making it possible to calculate the area in various scenarios. The area is always expressed in square units, reflecting the two-dimensional nature of the shape.
Area Calculation Methods
Calculating the area of a triangle can be achieved through several methods, depending on the available information. Here are some common methods:
1. Using Base and Height
This method is the most straightforward and is applicable to any type of triangle. The area (A) is calculated by multiplying the base (b) with the height (h) and then dividing by 2:
( A = frac{1}{2} imes b imes h )
For example, a triangle with a base of 5cm and a height of 3cm has an area of ( frac{1}{2} imes 5 imes 3 = 7.5 ) cm².
2. Using Side Lengths (Heron’s Formula)
When the lengths of all three sides are known, Heron\"s formula can be used. First, calculate the semi-perimeter (s) as ( s = frac{a + b + c}{2} ), where a, b, and c are the sides of the triangle. The area is then calculated using:
( A = sqrt{s imes (s - a) imes (s - b) imes (s - c)} )
3. Using Trigonometry
If two sides of a triangle and the included angle are known, the area can be calculated using trigonometric functions. For a triangle with sides a and b, and an included angle C, the area is:
( A = frac{1}{2} imes a imes b imes sin(C) )
These methods provide flexibility in calculating the area of a triangle, catering to different scenarios where certain measurements are known.
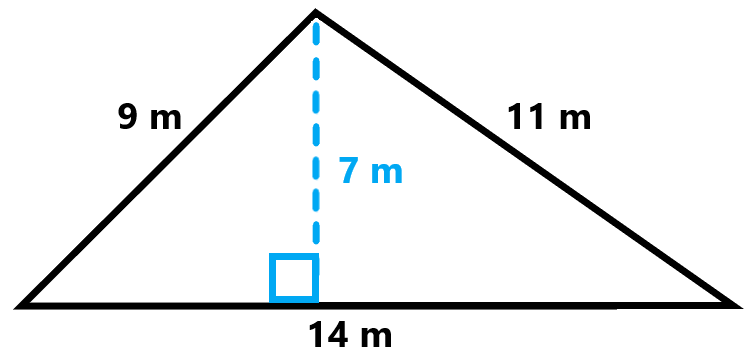
Special Formulas and Cases
There are several special formulas and cases for calculating the area and perimeter of triangles, which are particularly useful when dealing with specific types of triangles.
Special Formulas for Triangle Perimeter
- Equilateral Triangle: For an equilateral triangle with each side of length \"a\", the perimeter is simply ( P = 3a ).
- Isosceles Triangle: In an isosceles triangle with two equal sides of length \"a\" and a base \"b\", the perimeter is given by ( P = 2a + b ).
- Scalene Triangle: A scalene triangle has all sides of different lengths. If the sides are \"a\", \"b\", and \"c\", the perimeter is ( P = a + b + c ).
Special Formulas for Triangle Area
- Equilateral Triangle: The area of an equilateral triangle with side \"a\" is calculated using ( A = frac{sqrt{3}}{4} imes a^2 ).
- Scalene Triangle (Heron’s Formula): For a scalene triangle with sides \"a\", \"b\", and \"c\", first calculate the semi-perimeter ( s = frac{a + b + c}{2} ). Then, use Heron\"s formula ( A = sqrt{s(s - a)(s - b)(s - c)} ) to find the area.
- Using Pythagorean Theorem: In right triangles, you can use the Pythagorean Theorem to find missing sides, which can then be used to calculate the area using the basic formula ( A = frac{1}{2} imes ext{base} imes ext{height} ).
These formulas are essential tools for solving problems in geometry and have various practical applications, such as in construction and engineering.

_HOOK_
Practical Examples and Solved Problems
Understanding the area and perimeter of triangles is easier with practical examples and solved problems. Let\"s dive into some of these to grasp these concepts better.
- Example 1: Calculating the Area of a Triangle
- Consider a triangle with a base of 9 cm and a height of 6 cm. To find the area, use the formula (A = frac{1}{2} imes ext{base} imes ext{height}). Therefore, the area (A) is ( frac{1}{2} imes 9 imes 6 = 27 ext{ cm}^2).
- Example 2: Finding the Perimeter of a Triangle
- Imagine a triangle with sides measuring 7 cm, 8 cm, and 16 cm. The perimeter of a triangle is the sum of all its sides. Thus, the perimeter (P) is (7 + 8 + 16 = 31 ext{ cm}).
- Example 3: Area of a Right Triangle
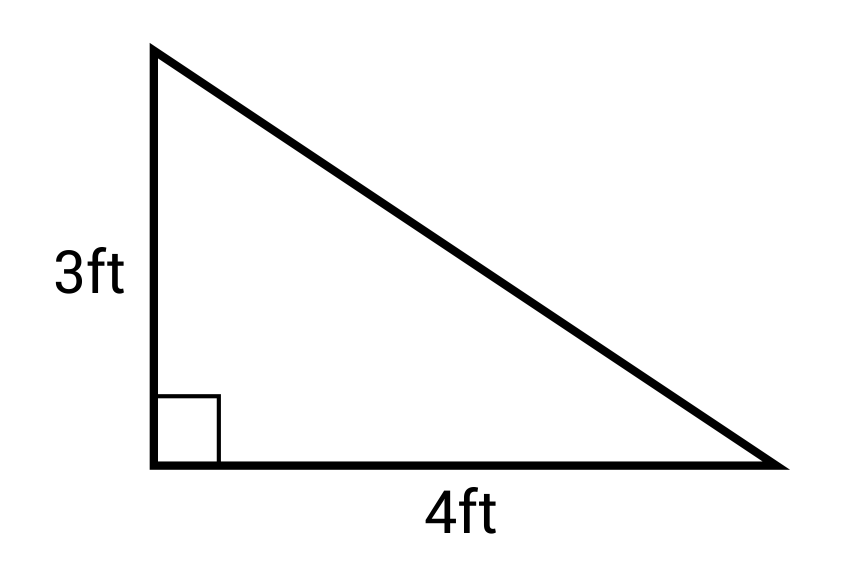
- For a right triangle with sides of 4 ft and 3 ft, the area can be calculated using the formula (A = frac{1}{2} imes ext{base} imes ext{height}), giving us (A = frac{1}{2} imes 4 imes 3 = 6 ext{ ft}^2).
- Example 4: Perimeter of a Triangle Using SAS
- For a triangle where two sides are 8 ft and 6 ft, and the angle between them is 75°, the perimeter can be found using the law of cosines. The perimeter in this case is approximately 22.67 ft.
- Example 5: Area of a Triangle Using Base and Height
- If a triangle has a base of 3 cm and a height of 4 cm, its area is calculated as (A = frac{1}{2} imes 3 imes 4 = 6 ext{ cm}^2).
These examples offer a clear understanding of how to approach problems related to the area and perimeter of triangles. Practicing these methods will enhance your ability to solve similar problems effectively.
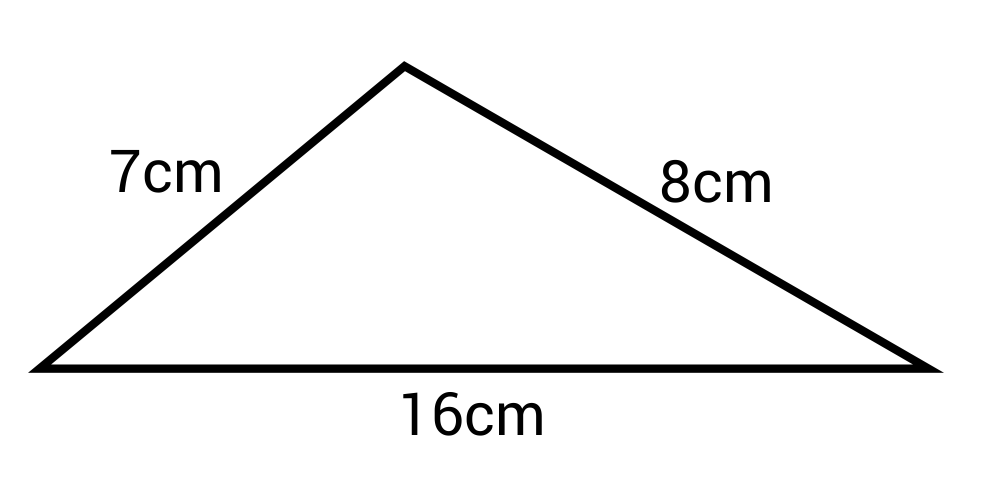
Interactive Practice Problems
Interactive exercises are an excellent way to reinforce your understanding of triangle area and perimeter. Below are some interactive problems for you to solve. After trying each problem, you can check your answers to see how well you\"re doing.
- Problem 1: Area Calculation
- Find the area of a triangle with a base of 6 units and a height of 7 units. Use the formula (A=frac{1}{2} imes ext{base} imes ext{height}).
- Problem 2: Perimeter Calculation
- Calculate the perimeter of a triangle with sides measuring 7 units, 8 units, and 16 units. Remember, the perimeter is the sum of all side lengths.
- Problem 3: Right Triangle Area
- For a right triangle with a base of 3 units and a height of 4 units, calculate its area.
- Problem 4: Determining Side Length
- A triangle has a perimeter of 25 cm. Two of its sides measure 4 cm and 10 cm. Find the length of the third side.
- Problem 5: Area of an Isosceles Right Triangle
- If one leg of an isosceles right triangle measures 17 inches, calculate its area.
After you\"ve attempted these problems, you can check your solutions. Interactive exercises like these help in better understanding and retention of mathematical concepts.

Application in Real-World Scenarios
Understanding the area and perimeter of triangles has numerous practical applications in everyday life. Here are some real-world scenarios where these concepts are crucial:
- Architecture and Construction: In architecture, the area and perimeter of triangular shapes are essential for designing roofs, bridges, and other structural elements. Triangular trusses, for example, are a common feature in bridge construction due to their strength and stability.
- Land Surveying and Real Estate: Calculating the area and perimeter of land parcels is critical in fields like real estate and land surveying. This helps in determining the size and boundaries of a property, which is essential for sales, development, and taxation.
- Astronomy and Space Exploration: In astronomy, calculating the area and perimeter of celestial bodies and their orbits helps in understanding their size, distance, and movement patterns.
- Computer Graphics and Gaming: In computer graphics, especially in the gaming industry, area and perimeter calculations are used to create and render realistic images and environments.
- Art and Fashion Design: Area and perimeter concepts are also applied in designing fashion and art pieces, ensuring the right proportions and dimensions are achieved.
- Education: These concepts are fundamental in education, helping students develop analytical and problem-solving skills.
- Everyday Examples: From determining the amount of paint needed for a wall to installing carpets or tiles, the concepts of area and perimeter are used in various everyday tasks.
These examples highlight the importance of understanding the area and perimeter of triangles in various industries and everyday life. Such knowledge is not only academically beneficial but also practical in many professional fields.

Advanced Concepts and Theorems
Understanding the advanced concepts and theorems in triangle geometry can greatly enhance your ability to solve complex problems related to triangle area and perimeter. Let\"s delve into some of these concepts:
The Law of Sines and Cosines
The Law of Sines and Cosines are crucial for solving triangles when standard formulas are not applicable, especially in non-right triangles.
- Law of Sines: Useful in ASA (angle-side-angle) or AAS (angle-angle-side) situations. It states that the ratio of the length of a side to the sine of its opposite angle is constant for all three sides and angles in a triangle.
- Law of Cosines: Essential in SAS (side-angle-side) or SSS (side-side-side) situations. It generalizes the Pythagorean theorem for any triangle, providing a formula to find a side length when two sides and the included angle are known, or an angle when all three sides are known.
Heron\"s Formula
Heron\"s Formula is a remarkable formula that allows you to calculate the area of a triangle when you know the lengths of all three sides. It first involves calculating the semi-perimeter (half of the perimeter) of the triangle, then applying the formula to find the area.
Area Calculation Using Trigonometry
For non-right triangles, trigonometry can be applied to find the area. This involves using the sine function in combination with the lengths of two sides and the included angle.
Special Triangle Cases
Understanding special triangles like equilateral and isosceles triangles can simplify calculations:
- Equilateral Triangle: Since all sides and angles are equal, simple formulas based on the side length can be used to find the area and perimeter.
- Isosceles Triangle: Knowing that two sides are equal allows for simplification of area and perimeter formulas, especially when the height is known or can be calculated.
These advanced concepts provide a deeper understanding and more tools for solving various problems related to triangles, be it in geometry, engineering, or architecture.

READ MORE:
Summary and Key Takeaways
Understanding the area and perimeter of a triangle is fundamental in geometry, and its applications are vast, ranging from everyday tasks to complex engineering problems. Here are the key points to remember:
Area of a Triangle
- The area is the region enclosed within the three sides of a triangle. The general formula for the area of a triangle is A = ½ × base × height.
- For right-angled triangles, the area can be calculated as half the product of the two sides that form the right angle.
- In cases where all sides are known but the height is not, Heron\"s formula can be used. This method involves calculating the semi-perimeter and then applying the formula to find the area.
- For triangles where two sides and the included angle are known, trigonometric functions such as the sine rule can be used to calculate the area.
Perimeter of a Triangle
- The perimeter of a triangle is the sum of the lengths of its three sides.
- For equilateral triangles, the perimeter is simply three times the length of one side.
- In isosceles triangles, the perimeter is the sum of the two equal sides and the base.
- For scalene triangles, each side length must be individually added to find the perimeter.
- When only two sides and the included angle are known, the law of cosines can be used to find the third side, which then allows for the calculation of the perimeter.
Remember, the understanding of these concepts is not only vital for solving geometrical problems but also for their practical applications in fields like architecture, design, and physics.
Mastering the calculation of a triangle\"s area and perimeter unlocks a world of geometric understanding, essential for academic success and practical applications in various fields. Embark on this enlightening journey to enhance your mathematical prowess and real-world problem-solving skills.

_HOOK_