Topic what's 6 squared: Welcome to our comprehensive guide on understanding and calculating 6 squared. In this article, we will explore the definition, importance, and applications of squaring the number 6. Whether you're a student, educator, or math enthusiast, this guide will provide you with clear and detailed insights into the concept of 6 squared.
Table of Content
- Understanding 6 Squared
- Introduction to Squaring Numbers
- Definition and Meaning of 6 Squared
- How to Calculate 6 Squared
- Mathematical Notation for Squaring
- Step-by-Step Calculation of 6 Squared
- Importance of Squaring in Mathematics
- Applications of Squaring in Real Life
- Examples of Perfect Squares
- Using Squared Numbers in Geometry
- Squaring in Algebra and Equations
- The Role of Squaring in Physics
- Understanding Exponents and Powers
- Square Roots and Their Relationship to Squaring
- Visualizing Squaring with Graphs and Diagrams
- Common Mistakes When Squaring Numbers
- Practice Problems for Squaring Numbers
- Advanced Topics Related to Squaring
- Conclusion: The Power of Squaring in Everyday Math
- YOUTUBE:
Understanding 6 Squared
When we talk about squaring a number, we're referring to multiplying the number by itself. The concept of squaring a number is an essential part of mathematics, especially in algebra and geometry.
Calculation of 6 Squared
The expression 6 squared is mathematically written as \(6^2\). This notation means multiplying the number 6 by itself:
\[
6^2 = 6 \times 6
\]
Performing the multiplication:
\[
6 \times 6 = 36
\]
Therefore, 6 squared equals 36.
Why Squaring is Important
Squaring numbers is used in various areas such as:
- Calculating areas of squares and rectangles.
- Solving quadratic equations in algebra.
- In the Pythagorean theorem to determine the length of sides in right triangles.
- Used in physics to calculate energy and work.
Square Numbers
Square numbers, also known as perfect squares, are the product of an integer multiplied by itself. Here are a few examples:
- \(1^2 = 1\)
- \(2^2 = 4\)
- \(3^2 = 9\)
- \(4^2 = 16\)
- \(5^2 = 25\)
- \(6^2 = 36\)
Practical Applications of Squaring
Understanding how to square numbers can help in various real-world scenarios such as:
- Designing square and rectangular layouts for construction.
- Calculating the energy consumption in electrical circuits.
- Determining the area covered by square tiles in flooring projects.

READ MORE:
Introduction to Squaring Numbers
Squaring a number is a fundamental mathematical operation that involves multiplying the number by itself. This concept is often represented using an exponent of 2. For example, the notation \( n^2 \) means \( n \times n \). Squaring is widely used in various fields, including algebra, geometry, and physics, due to its simplicity and importance in calculations.
Here's a step-by-step breakdown of how to square a number:
- Identify the number: The first step is to identify the number you want to square. Let's use 6 as our example.
- Multiply the number by itself: Multiply the number by itself to find the square. For 6, this is \( 6 \times 6 \).
- Calculate the product: Perform the multiplication to find the result. \( 6 \times 6 = 36 \).
The result of squaring the number 6 is 36, which can be written as \( 6^2 = 36 \).
Squaring numbers is not only a basic arithmetic skill but also a building block for more advanced mathematical concepts. Understanding how to square numbers prepares students for topics such as quadratic equations, area calculations, and more.
Definition and Meaning of 6 Squared
Squaring a number means multiplying the number by itself. When we talk about "6 squared," we are referring to the operation of multiplying 6 by 6. This can be expressed mathematically as:
\[
6^2 = 6 \times 6
\]
To further understand the meaning of 6 squared, let's break it down step by step:
- Identify the base number: In this case, the base number is 6.
- Understand the exponent: The exponent is 2, which indicates that the base number should be multiplied by itself.
- Perform the multiplication: Multiply 6 by 6:
\[
6 \times 6 = 36
\]
Therefore, the result of 6 squared is 36, which can be written as \( 6^2 = 36 \). This means that squaring the number 6 gives us a product of 36.
In practical terms, squaring is a common mathematical operation used in various applications such as calculating areas, solving algebraic equations, and analyzing data in physics and engineering.
How to Calculate 6 Squared
Calculating 6 squared is a simple process that involves multiplying the number 6 by itself. Here is a detailed, step-by-step guide on how to perform this calculation:
- Identify the number to be squared: The number we want to square is 6.
- Understand the squaring operation: Squaring a number means multiplying the number by itself. This is represented as:
\[
6^2
\] - Set up the multiplication: Write the multiplication expression:
\[
6 \times 6
\] - Perform the multiplication: Calculate the product of 6 and 6:
\[
6 \times 6 = 36
\]
Therefore, the result of 6 squared is 36. This can be written in mathematical notation as:
\[
6^2 = 36
\]
Understanding how to calculate squares is important for various mathematical applications, such as solving quadratic equations, calculating areas in geometry, and analyzing data in physics and engineering.
Mathematical Notation for Squaring
In mathematics, squaring a number involves multiplying that number by itself. This operation is commonly represented using an exponent of 2. The general notation for squaring a number \( n \) is \( n^2 \), which is read as "n squared." Here is a detailed explanation of the notation and its use:
- Base Number: The number that is being squared is referred to as the base. For example, in \( 6^2 \), the base number is 6.
- Exponent: The exponent indicates how many times the base number is multiplied by itself. In the case of squaring, the exponent is 2. This means:
\[
n^2 = n \times n
\] - Example Calculation: To square the number 6, we write:
\[
6^2
\]This means \( 6 \times 6 \), which equals 36.
Using this notation, we can easily represent and calculate squares of any number. Here are a few more examples:
- \( 3^2 = 3 \times 3 = 9 \)
- \( 5^2 = 5 \times 5 = 25 \)
- \( 7^2 = 7 \times 7 = 49 \)
Mathematical notation for squaring is fundamental in various areas of mathematics, including algebra, geometry, and calculus. It simplifies the representation of repeated multiplication and is essential for understanding higher-level mathematical concepts.
Step-by-Step Calculation of 6 Squared
Calculating 6 squared is straightforward and can be done in a few simple steps. Follow this detailed, step-by-step guide to understand how to square the number 6:
- Identify the number: The first step is to identify the number you want to square. In this case, the number is 6.
- Write the squaring expression: Express the operation of squaring the number 6 using mathematical notation:
\[
6^2
\] - Set up the multiplication: Squaring a number means multiplying it by itself. So, set up the multiplication expression:
\[
6^2 = 6 \times 6
\] - Perform the multiplication: Calculate the product of 6 and 6:
\[
6 \times 6 = 36
\]
Therefore, the result of squaring the number 6 is 36. This can be written as:
\[
6^2 = 36
\]
Squaring numbers is a basic arithmetic operation that is widely used in various mathematical contexts, including geometry, algebra, and physics. Understanding how to perform this operation is essential for solving more complex mathematical problems.
Importance of Squaring in Mathematics
Squaring numbers is a fundamental operation in mathematics with wide-ranging applications across various fields. Understanding the importance of squaring is crucial for grasping more advanced mathematical concepts. Here are some key reasons why squaring is important:
- Basic Arithmetic and Algebra: Squaring is one of the essential arithmetic operations. It is foundational for understanding exponents and powers, which are key concepts in algebra.
- Geometry: Squaring is used extensively in geometry to calculate areas of squares and other geometric shapes. For example, the area of a square with side length \( s \) is \( s^2 \).
- Pythagorean Theorem: In right-angled triangles, the squares of the lengths of the legs are related to the square of the hypotenuse. This relationship is expressed as \( a^2 + b^2 = c^2 \).
- Quadratic Equations: Squaring is integral to solving quadratic equations, which have the general form \( ax^2 + bx + c = 0 \). These equations appear frequently in various mathematical problems and applications.
- Physics and Engineering: Squaring is used in physics to describe relationships between different quantities, such as in calculating kinetic energy (\( E_k = \frac{1}{2}mv^2 \)), where \( m \) is mass and \( v \) is velocity.
- Statistics: Squaring deviations from the mean is a crucial step in calculating variance and standard deviation, which measure data dispersion in statistics.
Overall, the operation of squaring numbers is a fundamental building block in mathematics. Its applications span from simple arithmetic to complex scientific calculations, making it a critical concept to master for students and professionals alike.
Applications of Squaring in Real Life
Squaring numbers is not only a fundamental mathematical operation but also has numerous practical applications in real life. Here are some key areas where squaring is applied:
- Geometry and Area Calculation: Squaring is used to calculate the area of squares and other shapes. For example, if each side of a square is 6 units, the area is calculated as:
\[
\text{Area} = 6^2 = 36 \text{ square units}
\] - Physics and Engineering: In physics, squaring is used to calculate various quantities, such as the kinetic energy of an object, given by:
\[
E_k = \frac{1}{2}mv^2
\]where \( m \) is mass and \( v \) is velocity. This relationship shows how energy increases with the square of velocity.
- Finance: Squaring is used in financial calculations, such as in the compound interest formula, where the growth of investment is related to the square of time periods in some cases.
- Statistics: In statistics, squaring deviations from the mean is a crucial step in calculating variance and standard deviation, which are measures of data dispersion:
\[
\text{Variance} = \frac{\sum (x_i - \bar{x})^2}{N}
\]where \( x_i \) represents each data point, \( \bar{x} \) is the mean, and \( N \) is the number of data points.
- Agriculture: Farmers use squaring to calculate the area of land plots. Knowing the area helps in planning the planting and irrigation of crops efficiently.
- Architecture and Construction: Squaring is used in architecture and construction to determine materials needed for building projects, such as flooring, walls, and roofs. Accurate area calculations ensure proper material estimates and cost management.
These examples illustrate how squaring is an essential tool in various fields, contributing to practical solutions and advancements in everyday life.
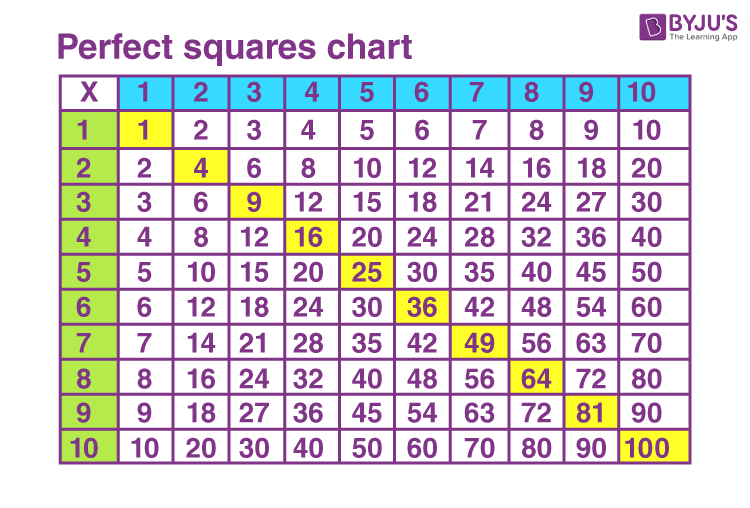
Examples of Perfect Squares
A perfect square is a number that can be expressed as the square of an integer. Perfect squares are important in various areas of mathematics, including algebra and geometry. Here are some examples of perfect squares:
- 1: The square of 1 is 1.
\[
1^2 = 1 \times 1 = 1
\] - 4: The square of 2 is 4.
\[
2^2 = 2 \times 2 = 4
\] - 9: The square of 3 is 9.
\[
3^2 = 3 \times 3 = 9
\] - 16: The square of 4 is 16.
\[
4^2 = 4 \times 4 = 16
\] - 25: The square of 5 is 25.
\[
5^2 = 5 \times 5 = 25
\] - 36: The square of 6 is 36.
\[
6^2 = 6 \times 6 = 36
\] - 49: The square of 7 is 49.
\[
7^2 = 7 \times 7 = 49
\] - 64: The square of 8 is 64.
\[
8^2 = 8 \times 8 = 64
\] - 81: The square of 9 is 81.
\[
9^2 = 9 \times 9 = 81
\] - 100: The square of 10 is 100.
\[
10^2 = 10 \times 10 = 100
\]
Recognizing perfect squares can be very useful in simplifying algebraic expressions, solving equations, and understanding geometric properties. These examples show how squaring integers produces perfect squares, which are integral parts of many mathematical concepts.

Using Squared Numbers in Geometry
Squared numbers play a crucial role in geometry, helping to calculate areas, distances, and other geometric properties. Here are some key ways squared numbers are used in geometry:
- Calculating Area: The area of a square is found by squaring the length of its sides. If each side of a square is 6 units, the area is:
\[
\text{Area} = 6^2 = 36 \text{ square units}
\] - Pythagorean Theorem: In a right-angled triangle, the squares of the lengths of the legs are related to the square of the hypotenuse. This relationship is expressed as:
\[
a^2 + b^2 = c^2
\]where \( a \) and \( b \) are the legs, and \( c \) is the hypotenuse.
- Distance Formula: The distance between two points in a plane can be calculated using the distance formula, which involves squaring the differences in coordinates:
\[
d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\] - Circle Area: The area of a circle is calculated using the radius squared. The formula is:
\[
\text{Area} = \pi r^2
\]where \( r \) is the radius of the circle.
- Volume of a Cube: The volume of a cube is found by cubing the length of its sides, which includes squaring for intermediate calculations:
\[
\text{Volume} = s^3 = s \times s^2
\]where \( s \) is the length of a side of the cube.
These examples demonstrate how squared numbers are fundamental to various geometric calculations. Understanding how to use squared numbers in geometry helps solve problems related to shapes, distances, and spatial relationships.
Squaring in Algebra and Equations
Squaring is a fundamental operation in algebra that appears frequently in equations. It involves multiplying a number by itself. The notation for squaring a number is to use the exponent 2. For example, \( 6 \) squared is written as \( 6^2 \) and calculated as follows:
\[
6^2 = 6 \times 6 = 36
\]
In algebra, squaring is used in various types of equations and expressions, including quadratic equations, which are equations of the form \( ax^2 + bx + c = 0 \). Here are some examples and applications of squaring in algebra:
- Solving Quadratic Equations: Quadratic equations often involve terms that are squared. For example, to solve \( x^2 + 6x + 9 = 0 \), you would use factoring, completing the square, or the quadratic formula.
- Expanding Binomials: The square of a binomial expression, such as \( (a + b)^2 \), expands to \( a^2 + 2ab + b^2 \). This is derived from the distributive property of multiplication.
- Graphing Parabolas: The graph of a quadratic function \( y = ax^2 + bx + c \) is a parabola. The vertex and direction of the parabola depend on the coefficients \( a \), \( b \), and \( c \).
Consider the quadratic equation example:
\[
x^2 - 4x + 4 = 0
\]
To solve this equation, we can factor it as follows:
\[
(x - 2)^2 = 0
\]
Setting each factor equal to zero gives us the solution:
\[
x - 2 = 0 \implies x = 2
\]
Thus, the solution to the equation is \( x = 2 \).
Here's another example involving the quadratic formula. For the equation \( ax^2 + bx + c = 0 \), the solutions can be found using:
\[
x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
\]
For \( x^2 - 6x + 9 = 0 \), where \( a = 1 \), \( b = -6 \), and \( c = 9 \), the quadratic formula gives:
\[
x = \frac{6 \pm \sqrt{(-6)^2 - 4 \cdot 1 \cdot 9}}{2 \cdot 1} = \frac{6 \pm \sqrt{36 - 36}}{2} = \frac{6 \pm 0}{2} = 3
\]
This confirms that the solutions to the equation are \( x = 3 \).
Squaring also appears in inequalities and other algebraic contexts, making it a versatile and important concept in mathematics.
The Role of Squaring in Physics
Squaring numbers plays a crucial role in various aspects of physics. Here are some key areas where squaring is essential:
-
Kinetic Energy:
The formula for kinetic energy of an object is given by:
\( KE = \frac{1}{2} mv^2 \)
In this equation, \( m \) is the mass of the object and \( v \) is its velocity. The velocity is squared, showing how the kinetic energy increases with the square of the velocity.
-
Gravitational Force:
Newton's law of universal gravitation is expressed as:
\( F = G \frac{m_1 m_2}{r^2} \)
Here, \( F \) is the gravitational force between two masses \( m_1 \) and \( m_2 \), \( G \) is the gravitational constant, and \( r \) is the distance between the centers of the two masses. The force is inversely proportional to the square of the distance.
-
Electric Force:
Coulomb's law for the electric force between two charges is:
\( F = k_e \frac{q_1 q_2}{r^2} \)
In this formula, \( F \) is the force, \( q_1 \) and \( q_2 \) are the magnitudes of the charges, \( r \) is the distance between the charges, and \( k_e \) is Coulomb's constant. Similar to gravitational force, the electric force is inversely proportional to the square of the distance between the charges.
-
Intensity of Light:
The intensity of light from a point source follows the inverse square law:
\( I = \frac{P}{4 \pi r^2} \)
Here, \( I \) is the intensity, \( P \) is the power of the source, and \( r \) is the distance from the source. The intensity diminishes with the square of the distance from the light source.
-
Wave Propagation:
The amplitude of waves, such as sound or electromagnetic waves, decreases with the square of the distance from the source. This principle is crucial in understanding how waves propagate through different media.
These examples illustrate the importance of squaring in physics, highlighting how fundamental physical laws and principles often rely on squared terms to describe natural phenomena accurately.
Understanding Exponents and Powers
Exponents and powers are fundamental concepts in mathematics that simplify the representation and computation of repeated multiplication. Here's a detailed explanation of these concepts:
Definition of Exponents:
An exponent refers to the number of times a base number is multiplied by itself. It is written as a small number to the upper right of the base number. For example, \( 6^2 \) (read as "six squared") means 6 multiplied by itself:
\[ 6^2 = 6 \times 6 = 36 \]
General Form:
The general form of an exponent is \( a^n \), where:
- \( a \) is the base
- \( n \) is the exponent or power
This represents the base \( a \) multiplied by itself \( n \) times.
Properties of Exponents:
- Product of Powers: When multiplying like bases, add the exponents. \[ a^m \times a^n = a^{m+n} \]
- Quotient of Powers: When dividing like bases, subtract the exponents. \[ \frac{a^m}{a^n} = a^{m-n} \]
- Power of a Power: Multiply the exponents. \[ (a^m)^n = a^{m \times n} \]
- Power of a Product: Apply the exponent to each factor. \[ (ab)^n = a^n \times b^n \]
- Zero Exponent: Any nonzero number raised to the power of zero equals one. \[ a^0 = 1 \]
- Negative Exponent: A negative exponent represents the reciprocal of the base raised to the opposite positive exponent. \[ a^{-n} = \frac{1}{a^n} \]
Examples of Exponents:
| Expression | Expanded Form | Value |
|---|---|---|
| \( 2^3 \) | \( 2 \times 2 \times 2 \) | 8 |
| \( 5^2 \) | \( 5 \times 5 \) | 25 |
| \( 10^0 \) | - | 1 |
| \( 4^{-2} \) | \( \frac{1}{4 \times 4} \) | \( \frac{1}{16} \) |
Understanding exponents and powers is essential for mastering more advanced mathematical concepts and operations, providing a foundation for algebra, calculus, and beyond.

Square Roots and Their Relationship to Squaring
Square roots are closely related to squaring numbers. Understanding this relationship is fundamental to many mathematical concepts.
Definition of Square Roots:
The square root of a number is a value that, when multiplied by itself, gives the original number. It is denoted by the radical symbol \( \sqrt{} \). For example, the square root of 36 is written as \( \sqrt{36} \), which equals 6, because:
\[ 6 \times 6 = 36 \]
Relationship Between Squaring and Square Roots:
- Squaring a number and then taking the square root of the result returns the original number. \[ \sqrt{(a^2)} = a \] For instance, \( \sqrt{(6^2)} = \sqrt{36} = 6 \).
- Similarly, taking the square root of a number and then squaring the result returns the original number. \[ (\sqrt{a})^2 = a \] For example, \( (\sqrt{36})^2 = 6^2 = 36 \).
Properties of Square Roots:
- Non-Negative Results: The principal square root of a non-negative number is always non-negative. \[ \sqrt{a} \geq 0 \text{ for } a \geq 0 \]
- Product Property: The square root of a product is the product of the square roots. \[ \sqrt{ab} = \sqrt{a} \times \sqrt{b} \]
- Quotient Property: The square root of a quotient is the quotient of the square roots. \[ \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \]
Examples of Square Roots:
| Number | Square Root | Verification |
|---|---|---|
| 25 | \( \sqrt{25} = 5 \) | \( 5 \times 5 = 25 \) |
| 49 | \( \sqrt{49} = 7 \) | \( 7 \times 7 = 49 \) |
| 64 | \( \sqrt{64} = 8 \) | \( 8 \times 8 = 64 \) |
Applications of Square Roots:
- Geometry: Finding the side length of a square when its area is known.
- Physics: Calculating quantities like root mean square velocity in kinetic theory of gases.
- Statistics: Standard deviation is often found using square roots.
Understanding square roots and their relationship to squaring numbers is essential for solving equations, understanding geometric properties, and working with various scientific and statistical formulas.
Visualizing Squaring with Graphs and Diagrams
Understanding the concept of squaring numbers can be greatly enhanced by visualizing them through graphs and diagrams. Here are some ways to visualize squaring:
Graph of a Quadratic Function:
The function \( y = x^2 \) represents the relationship between a number \( x \) and its square. The graph of this function is a parabola that opens upwards.
Here's the graph of \( y = x^2 \):

The graph shows that for each value of \( x \), the corresponding \( y \)-value is \( x \) squared. For example, when \( x = 6 \), \( y = 6^2 = 36 \).
Square Diagrams:
A square diagram can also help to visualize squaring. Consider a square with a side length of 6 units. The area of the square represents the square of the side length:
\[ \text{Area} = \text{side length} \times \text{side length} = 6 \times 6 = 36 \text{ square units} \]

This diagram visually demonstrates that squaring the side length (6 units) results in an area of 36 square units.
Table of Values:
Another way to visualize squaring is by using a table of values, showing the relationship between numbers and their squares:
| \( x \) | \( x^2 \) |
|---|---|
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
| 5 | 25 |
| 6 | 36 |
| 7 | 49 |
| 8 | 64 |
| 9 | 81 |
| 10 | 100 |
This table shows that as \( x \) increases, \( x^2 \) increases more rapidly, illustrating the exponential growth of squared values.
Visual tools such as graphs, diagrams, and tables can make the concept of squaring numbers more intuitive and easier to grasp, providing a clearer understanding of the mathematical relationships involved.
Common Mistakes When Squaring Numbers
While squaring numbers is a fundamental mathematical operation, it is common for students to make mistakes. Here are some frequent errors and tips to avoid them:
- Confusing Squaring with Doubling:
One common mistake is thinking that squaring a number is the same as doubling it. Squaring means multiplying the number by itself, not by two.
Example:
\( 6^2 = 6 \times 6 = 36 \), not \( 6 \times 2 = 12 \).
- Incorrectly Squaring Negative Numbers:
When squaring negative numbers, remember that the result is positive because a negative times a negative is positive.
Example:
\( (-6)^2 = -6 \times -6 = 36 \), not \(-36\).
- Misinterpreting the Order of Operations:
It is crucial to follow the order of operations (PEMDAS/BODMAS). Squaring should be done before addition, subtraction, multiplication, or division unless parentheses dictate otherwise.
Example:
\( 3 + 4^2 \neq (3 + 4)^2 \)
\( 3 + 4^2 = 3 + 16 = 19 \)
\( (3 + 4)^2 = 7^2 = 49 \)
- Forgetting to Apply the Exponent to the Entire Base:
When squaring a term with more than one factor, ensure that the exponent applies to the entire base.
Example:
\( (2x)^2 = 2^2 \times x^2 = 4x^2 \), not \( 2 \times x^2 = 2x^2 \).
- Misusing the Distributive Property:
When squaring a binomial, apply the distributive property correctly. The formula for squaring a binomial is:
\( (a + b)^2 = a^2 + 2ab + b^2 \)
Example:
\( (3 + 4)^2 = 3^2 + 2 \cdot 3 \cdot 4 + 4^2 = 9 + 24 + 16 = 49 \), not \( 3^2 + 4^2 = 9 + 16 = 25 \).
Examples of Correct Squaring:
| Expression | Calculation | Result |
|---|---|---|
| \( 5^2 \) | \( 5 \times 5 \) | 25 |
| \( (-7)^2 \) | \( -7 \times -7 \) | 49 |
| \( (2x)^2 \) | \( 2^2 \times x^2 \) | 4x^2 |
| \( (3 + 2)^2 \) | \( 3^2 + 2 \cdot 3 \cdot 2 + 2^2 \) | 25 |
By recognizing and avoiding these common mistakes, students can improve their accuracy and confidence in squaring numbers.
Practice Problems for Squaring Numbers
Practicing squaring numbers helps solidify understanding and improves calculation skills. Here are some practice problems to help you master the concept of squaring numbers.
Basic Squaring Problems:
- Square the number 3.
- Square the number 7.
- Square the number 10.
- Square the number 15.
- Square the number 25.
Intermediate Squaring Problems:
- Square the number -4.
- Square the number -9.
- Square the number 12.5.
- Square the number 0.6.
- Square the number -3.3.
Advanced Squaring Problems:
- Square the binomial \( (x + 2) \).
- Square the binomial \( (3y - 5) \).
- Square the expression \( (2a + 3b) \).
- Square the trinomial \( (x + y + z) \).
- Square the complex number \( (3 + 4i) \).
Step-by-Step Solutions:
- Square the number 3: \[ 3^2 = 3 \times 3 = 9 \]
- Square the number 7: \[ 7^2 = 7 \times 7 = 49 \]
- Square the number 10: \[ 10^2 = 10 \times 10 = 100 \]
- Square the number 15: \[ 15^2 = 15 \times 15 = 225 \]
- Square the number 25: \[ 25^2 = 25 \times 25 = 625 \]
- Square the number -4: \[ (-4)^2 = (-4) \times (-4) = 16 \]
- Square the number -9: \[ (-9)^2 = (-9) \times (-9) = 81 \]
- Square the number 12.5: \[ (12.5)^2 = 12.5 \times 12.5 = 156.25 \]
- Square the number 0.6: \[ (0.6)^2 = 0.6 \times 0.6 = 0.36 \]
- Square the number -3.3: \[ (-3.3)^2 = (-3.3) \times (-3.3) = 10.89 \]
- Square the binomial \( (x + 2) \): \[ (x + 2)^2 = x^2 + 2 \cdot x \cdot 2 + 2^2 = x^2 + 4x + 4 \]
- Square the binomial \( (3y - 5) \): \[ (3y - 5)^2 = (3y)^2 - 2 \cdot 3y \cdot 5 + (-5)^2 = 9y^2 - 30y + 25 \]
- Square the expression \( (2a + 3b) \): \[ (2a + 3b)^2 = (2a)^2 + 2 \cdot 2a \cdot 3b + (3b)^2 = 4a^2 + 12ab + 9b^2 \]
- Square the trinomial \( (x + y + z) \): \[ (x + y + z)^2 = x^2 + y^2 + z^2 + 2xy + 2xz + 2yz \]
- Square the complex number \( (3 + 4i) \): \[ (3 + 4i)^2 = 3^2 + 2 \cdot 3 \cdot 4i + (4i)^2 = 9 + 24i + 16(-1) = -7 + 24i \]
Practicing these problems will help you become more confident and accurate in squaring numbers, whether they are integers, fractions, binomials, trinomials, or complex numbers.

Advanced Topics Related to Squaring
Squaring numbers is a foundational concept in mathematics, but it also extends to more advanced topics. Here are some advanced topics related to squaring:
1. Polynomial Equations:
Squaring is crucial in solving polynomial equations, especially quadratic equations. A quadratic equation takes the form:
\[ ax^2 + bx + c = 0 \]
Solutions to quadratic equations can be found using the quadratic formula:
\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
2. Completing the Square:
Completing the square is a technique used to solve quadratic equations and to derive the quadratic formula. The process involves rewriting a quadratic equation in the form:
\[ ax^2 + bx + c = a(x - h)^2 + k \]
where \( h \) and \( k \) are constants. This form makes it easier to analyze the properties of the quadratic function.
3. Binomial Theorem:
The Binomial Theorem provides a way to expand binomials raised to a power. For squaring a binomial, it states:
\[ (a + b)^2 = a^2 + 2ab + b^2 \]
For higher powers, the theorem generalizes to:
\[ (a + b)^n = \sum_{k=0}^{n} \binom{n}{k} a^{n-k} b^k \]
4. Squaring in Complex Numbers:
Squaring complex numbers involves both real and imaginary parts. For a complex number \( z = a + bi \), squaring is done as follows:
\[ z^2 = (a + bi)^2 = a^2 + 2abi + (bi)^2 = a^2 - b^2 + 2abi \]
This results in a new complex number with both real and imaginary parts.
5. Matrix Squaring:
In linear algebra, squaring a matrix involves matrix multiplication. For a matrix \( A \), squaring is given by:
\[ A^2 = A \times A \]
Matrix squaring is used in various applications, including solving systems of linear equations and finding powers of matrices.
6. Squaring in Calculus:
In calculus, squaring functions can help in finding areas under curves and solving integrals. For example, the integral of a squared function is:
\[ \int (f(x))^2 \, dx \]
Squaring functions also appear in Taylor series expansions and in solving differential equations.
Examples and Practice Problems:
- Solve the quadratic equation \( 2x^2 - 4x + 1 = 0 \) using the quadratic formula.
- Complete the square for the quadratic expression \( x^2 + 6x + 9 \).
- Expand \( (3x + 2)^2 \) using the Binomial Theorem.
- Square the complex number \( 1 + 3i \).
- Find \( A^2 \) for the matrix \( A = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} \).
- Evaluate the integral \( \int (x^2 + 2x + 1)^2 \, dx \).
These advanced topics demonstrate the wide-ranging applications and importance of squaring in various areas of mathematics and its related fields.
Conclusion: The Power of Squaring in Everyday Math
Squaring numbers is a fundamental mathematical operation that has far-reaching implications in various aspects of everyday life. Understanding the power of squaring enhances our mathematical proficiency and enables us to tackle more complex problems.
Applications of Squaring in Daily Life:
- Area Calculation: Squaring is essential for determining the area of squares and rectangles. For instance, if you need to find the area of a square with a side length of 6 units, you would calculate:
- Physics and Engineering: Squaring is used in various formulas in physics and engineering. For example, the kinetic energy (\( KE \)) of an object is given by:
- Statistics: In statistics, squaring is used to calculate the variance and standard deviation, which are measures of how spread out a data set is. The variance is the average of the squared differences from the mean.
- Financial Calculations: Squaring is used in finance to calculate compound interest and to model the growth of investments over time. The formula for compound interest includes an exponent, which involves repeated squaring.
\[ 6^2 = 36 \text{ square units} \]
\[ KE = \frac{1}{2}mv^2 \]
where \( m \) is the mass and \( v \) is the velocity. Here, velocity is squared to determine the kinetic energy.
Educational Benefits:
- Building Blocks for Advanced Math: Squaring numbers is a foundational skill that prepares students for more advanced topics such as algebra, calculus, and beyond.
- Improving Problem-Solving Skills: Regular practice with squaring numbers enhances problem-solving skills and mathematical thinking, which are crucial for academic and professional success.
Practice Problems to Reinforce Learning:
| Problem | Solution |
|---|---|
| Square the number 8 | \( 8^2 = 64 \) |
| Find the area of a square with a side length of 12 units | \( 12^2 = 144 \text{ square units} \) |
| Calculate the kinetic energy of an object with mass 5 kg and velocity 3 m/s | \( KE = \frac{1}{2} \times 5 \times 3^2 = 22.5 \text{ J} \) |
| Find the variance of the data set [4, 7, 10] | Mean = 7, Variance = \( \frac{(4-7)^2 + (7-7)^2 + (10-7)^2}{3} = 6 \) |
In conclusion, mastering the concept of squaring numbers is not just an academic exercise but a practical skill that enhances various aspects of everyday life. From calculating areas and energies to understanding financial growth and statistical measures, the power of squaring is evident in many fields. Continuous practice and application of this concept will strengthen mathematical understanding and proficiency.
Có sự khác biệt không? -6 bình phương so với (-6) bình phương so với 6 bình phương
READ MORE:
6 bình phương là bao nhiêu?