Topic 3 square root 18: Discover how to simplify and understand the calculation of 3 square root 18 in this comprehensive guide. Learn the step-by-step process, explore mathematical properties, and see real-life applications of square roots. Perfect for students, educators, and math enthusiasts seeking a clear and concise explanation.
Table of Content
- Calculation of \(3 \sqrt{18}\)
- Introduction to Square Roots
- Basics of Square Root Calculation
- Prime Factorization Method for Simplifying Square Roots
- Step-by-Step Calculation of \(3 \sqrt{18}\)
- Understanding the Simplification Process
- Mathematical Properties of Square Roots
- Examples and Practice Problems
- Applications of Square Roots in Real Life
- Common Mistakes and How to Avoid Them
- Additional Resources and Further Reading
- Conclusion and Summary
- YOUTUBE:
Calculation of \(3 \sqrt{18}\)
To calculate \(3 \sqrt{18}\), we start by simplifying the square root of 18:
- The prime factorization of 18 is \(18 = 2 \times 3^2\).
- Therefore, \(\sqrt{18} = \sqrt{2 \times 3^2} = \sqrt{2} \times \sqrt{3^2} = \sqrt{2} \times 3 = 3 \sqrt{2}\).
Now, we multiply by 3:
- \(3 \sqrt{18} = 3 \times 3 \sqrt{2} = 9 \sqrt{2}\).
Hence, the simplified form of \(3 \sqrt{18}\) is:
\[3 \sqrt{18} = 9 \sqrt{2}\]
READ MORE:
Introduction to Square Roots
Square roots are fundamental concepts in mathematics, representing a number that, when multiplied by itself, gives the original number. Understanding square roots is crucial for various mathematical operations and real-life applications.
The square root of a number \(x\) is denoted as \(\sqrt{x}\) and is defined as the value \(y\) such that \(y^2 = x\).
For example, \(\sqrt{16} = 4\) because \(4^2 = 16\).
Square roots can be categorized into two types:
- Perfect Square Roots: These are square roots of perfect squares, such as 1, 4, 9, 16, etc. For instance, \(\sqrt{9} = 3\) because \(3^2 = 9\).
- Non-Perfect Square Roots: These are square roots of non-perfect squares, which often result in irrational numbers. For example, \(\sqrt{2}\) is approximately 1.414 and cannot be expressed as a simple fraction.
To better understand square roots, let's explore their properties:
- Property 1: \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\). For instance, \(\sqrt{18} = \sqrt{2 \times 9} = \sqrt{2} \times \sqrt{9} = \sqrt{2} \times 3 = 3 \sqrt{2}\).
- Property 2: \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\). For example, \(\sqrt{\frac{4}{9}} = \frac{\sqrt{4}}{\sqrt{9}} = \frac{2}{3}\).
- Property 3: The square root of a square is the absolute value of the original number: \(\sqrt{x^2} = |x|\). For example, \(\sqrt{(-4)^2} = 4\).
Understanding these properties helps in simplifying complex square root expressions and solving equations involving square roots. In the next sections, we will delve deeper into calculating specific square roots, such as \(3 \sqrt{18}\), and explore their applications.
Basics of Square Root Calculation
The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 9 is 3 because \(3 \times 3 = 9\). The symbol for square root is \(\sqrt{}\).
Here are the steps to calculate the square root of a number:
- Identify the number you want to find the square root of: This is the number under the square root symbol.
- Prime Factorization: Break down the number into its prime factors. Prime factors are numbers that are only divisible by 1 and themselves. For example, the prime factors of 18 are 2 and 3.
- Pair the prime factors: For each pair of prime factors, one number comes out of the square root. If there is an unpaired factor, it remains under the square root. For example, in \(\sqrt{18}\), the prime factors are \(2 \times 3^2\), so we can write this as \(\sqrt{2 \times 3^2}\).
- Simplify the expression: Take out the paired factors. In the case of \(\sqrt{2 \times 3^2}\), we can take out the pair of 3s to get \(3\sqrt{2}\).
- Multiply any coefficients: If there is a coefficient outside the square root, multiply it by the simplified square root. For example, \(3 \sqrt{2}\) is the simplified form of \(\sqrt{18}\).
Let’s look at another example for better understanding:
- Example: Find the square root of 50.
- Step 1: Identify the number: 50.
- Step 2: Prime factorize 50: \(50 = 2 \times 5^2\).
- Step 3: Pair the prime factors: \(2 \times 5^2\) (we have a pair of 5s).
- Step 4: Simplify: \(\sqrt{2 \times 5^2} = 5 \sqrt{2}\).
This process can be applied to any number to find its square root, making it easier to understand and solve complex problems involving square roots.
Prime Factorization Method for Simplifying Square Roots
The prime factorization method is an efficient way to simplify square roots by breaking down the number inside the square root into its prime factors. Here is a step-by-step guide to simplifying \( \sqrt{18} \) using the prime factorization method:
-
Find the prime factors of 18:
- 18 is an even number, so it is divisible by 2.
- \(18 \div 2 = 9\)
- 9 is divisible by 3 (since 9 = 3 * 3).
- So, the prime factors of 18 are \(2 \times 3 \times 3\) or \(2 \times 3^2\).
-
Rewrite the square root of 18 using its prime factors:
\[
\sqrt{18} = \sqrt{2 \times 3^2}
\] -
Simplify the square root by separating the prime factors:
\[
\sqrt{2 \times 3^2} = \sqrt{2} \times \sqrt{3^2}
\] -
Evaluate the square root of the perfect square (if any):
\[
\sqrt{3^2} = 3
\] -
Combine the simplified parts:
\[
\sqrt{18} = 3 \sqrt{2}
\] -
Apply the multiplication with the number 3 outside the square root:
\[
3 \sqrt{18} = 3 \times 3 \sqrt{2} = 9 \sqrt{2}
\]
Therefore, the simplified form of \(3 \sqrt{18}\) is \(9 \sqrt{2}\).
Step-by-Step Calculation of \(3 \sqrt{18}\)
Calculating \(3 \sqrt{18}\) involves simplifying the square root first and then multiplying by the coefficient outside the square root. Here is a detailed step-by-step guide:
-
Express 18 in terms of its prime factors:
- 18 can be factored into \(2 \times 3 \times 3\) or \(2 \times 3^2\).
-
Rewrite the square root of 18 using its prime factors:
\[
\sqrt{18} = \sqrt{2 \times 3^2}
\] -
Simplify the square root by separating the perfect square from the other factors:
\[
\sqrt{2 \times 3^2} = \sqrt{2} \times \sqrt{3^2}
\] -
Evaluate the square root of the perfect square:
\[
\sqrt{3^2} = 3
\] -
Combine the simplified parts:
\[
\sqrt{18} = 3 \sqrt{2}
\] -
Now, multiply this result by the coefficient outside the square root:
\[
3 \sqrt{18} = 3 \times 3 \sqrt{2} = 9 \sqrt{2}
\]
Therefore, the step-by-step calculation shows that \(3 \sqrt{18}\) simplifies to \(9 \sqrt{2}\).
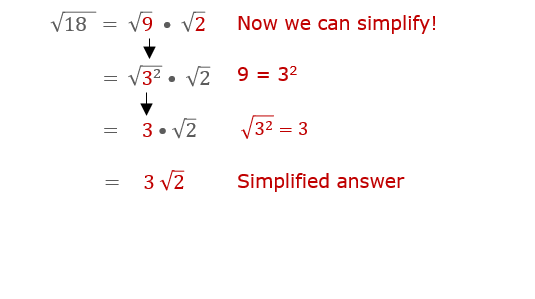
Understanding the Simplification Process
The simplification process for square roots involves breaking down the number inside the square root into its prime factors and then simplifying by extracting any perfect squares. Here is a detailed explanation of the simplification process for \(3 \sqrt{18}\):
-
Start with the number inside the square root, which is 18. Find the prime factors of 18:
- 18 can be factored into \(2 \times 3 \times 3\) or \(2 \times 3^2\).
-
Rewrite the square root of 18 using its prime factors:
\[
\sqrt{18} = \sqrt{2 \times 3^2}
\] -
Separate the perfect square from the other factors:
\[
\sqrt{2 \times 3^2} = \sqrt{2} \times \sqrt{3^2}
\] -
Evaluate the square root of the perfect square:
\[
\sqrt{3^2} = 3
\] -
Combine the simplified parts:
\[
\sqrt{18} = 3 \sqrt{2}
\] -
Now multiply this result by the coefficient outside the square root:
\[
3 \sqrt{18} = 3 \times 3 \sqrt{2} = 9 \sqrt{2}
\]
This process shows that \(3 \sqrt{18}\) simplifies to \(9 \sqrt{2}\). By breaking down the number inside the square root and extracting any perfect squares, we can simplify the expression effectively.
Mathematical Properties of Square Roots
Square roots have several interesting and useful properties. Understanding these properties helps in simplifying expressions and solving equations involving square roots. Here are some key properties:
- Perfect Squares: If a number is a perfect square, its square root will be a whole number. For example, \( \sqrt{100} = 10 \).
- Positive and Negative Roots: The square root of a number \( x \) has both positive and negative values, represented as \( \pm \sqrt{x} \). For example, \( \sqrt{9} = \pm 3 \).
- Product Property: The square root of a product is equal to the product of the square roots of the factors: \(\sqrt{xy} = \sqrt{x} \cdot \sqrt{y} \). For example, \( \sqrt{18} = \sqrt{9 \times 2} = \sqrt{9} \cdot \sqrt{2} = 3\sqrt{2} \).
- Quotient Property: The square root of a quotient is equal to the quotient of the square roots of the numerator and the denominator: \(\sqrt{\frac{x}{y}} = \frac{\sqrt{x}}{\sqrt{y}} \). For example, \( \sqrt{\frac{25}{4}} = \frac{\sqrt{25}}{\sqrt{4}} = \frac{5}{2} \).
- Exponent Form: The square root of a number can be expressed as an exponent of \( \frac{1}{2} \): \( \sqrt{x} = x^{\frac{1}{2}} \).
- Even and Odd Properties: The square root of an even number is even, and the square root of an odd number is odd. For example, \( \sqrt{64} = 8 \) (even), and \( \sqrt{121} = 11 \) (odd).
- Zero Property: The square root of zero is zero: \( \sqrt{0} = 0 \).
- Negative Numbers: The square root of a negative number does not exist in the set of real numbers. Instead, it is represented in the set of complex numbers. For example, \( \sqrt{-9} = 3i \), where \( i \) is the imaginary unit (\( i = \sqrt{-1} \)).
These properties are essential tools for simplifying expressions and solving mathematical problems involving square roots. They form the foundation for more advanced mathematical concepts and applications.
Examples and Practice Problems
Understanding how to work with square roots is crucial for solving many mathematical problems. Below are several examples and practice problems to help you master the concept of simplifying square roots, specifically focusing on the expression \(3 \sqrt{18}\).
Example Problems
-
Problem: Simplify \(3 \sqrt{18}\).
Solution:
- First, simplify the square root of 18.
- \(\sqrt{18} = \sqrt{9 \times 2} = \sqrt{9} \times \sqrt{2} = 3 \sqrt{2}\)
- Next, multiply by 3.
- \(3 \sqrt{18} = 3 \times 3 \sqrt{2} = 9 \sqrt{2}\)
Final Answer: \(9 \sqrt{2}\)
- First, simplify the square root of 18.
-
Problem: Simplify \(4 \sqrt{50}\).
Solution:
- Simplify the square root of 50.
- \(\sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} = 5 \sqrt{2}\)
- Multiply by 4.
- \(4 \sqrt{50} = 4 \times 5 \sqrt{2} = 20 \sqrt{2}\)
Final Answer: \(20 \sqrt{2}\)
- Simplify the square root of 50.
-
Problem: Simplify \(2 \sqrt{32}\).
Solution:
- Simplify the square root of 32.
- \(\sqrt{32} = \sqrt{16 \times 2} = \sqrt{16} \times \sqrt{2} = 4 \sqrt{2}\)
- Multiply by 2.
- \(2 \sqrt{32} = 2 \times 4 \sqrt{2} = 8 \sqrt{2}\)
Final Answer: \(8 \sqrt{2}\)
- Simplify the square root of 32.
Practice Problems
-
Simplify \(5 \sqrt{75}\).
-
Simplify \(7 \sqrt{45}\).
-
Simplify \(6 \sqrt{27}\).
-
Simplify \(8 \sqrt{18}\).
-
Simplify \(3 \sqrt{72}\).
Attempt these practice problems and check your answers using the steps provided in the examples. Simplifying square roots can become second nature with consistent practice!
Applications of Square Roots in Real Life
Square roots play a crucial role in various real-life applications across different fields. Below are some notable examples:
- Finance: Square roots are used in calculating stock market volatility, helping investors assess risk. For example, the standard deviation, a measure of volatility, is the square root of the variance of stock returns.
- Architecture and Engineering: Square roots are used to determine the natural frequencies of structures, such as bridges and buildings, ensuring they can withstand environmental forces like wind and traffic.
- Science: Calculations involving the velocity of moving objects, radiation absorption, and sound intensity often utilize square roots to derive meaningful data.
- Statistics: In statistical analysis, square roots are used to calculate standard deviation, which measures data dispersion. For example, if the variance of a data set is 16, the standard deviation is the square root of 16, which is 4.
- Geometry: The Pythagorean theorem, essential in geometry, involves square roots to find the length of the sides of right triangles. For example, in a right triangle with sides of length 3 and 4, the hypotenuse is √(32 + 42) = √25 = 5.
- Computer Science: Square roots are used in algorithms for encryption, image processing, and game physics. For example, calculating the distance between points in 3D space often involves square roots.
- Navigation: Pilots and sailors use square roots to compute distances between locations on maps or globes. The distance formula √((x2 - x1)2 + (y2 - y1)2) is derived from the Pythagorean theorem.
- Electrical Engineering: Calculations involving power, voltage, and current in circuits often require square roots. For example, the RMS (root mean square) value of an alternating current is calculated using the square root of the mean of the squares of the current values.
- Cooking: When scaling recipes, square roots help adjust ingredient quantities correctly. For example, to double a recipe, you might use the square root of 2 to find the correct scaling factor for certain ingredients.
- Photography: The f-number of a camera lens, which controls light exposure, is related to the square root of the aperture area. A lower f-number (larger aperture) allows more light to enter the camera.
These examples demonstrate the versatility and importance of square roots in solving practical problems and enhancing our understanding of various phenomena.

Common Mistakes and How to Avoid Them
When dealing with square roots and their simplifications, several common mistakes can occur. Understanding these errors and learning how to avoid them is crucial for mastering the concept.
-
Incorrect Simplification:
One common mistake is simplifying the square root incorrectly. For example, some might incorrectly simplify \( \sqrt{18} \) directly to \( 9 \) instead of correctly simplifying it to \( 3\sqrt{2} \).
To avoid this, use the prime factorization method:
- Prime factorize 18: \( 18 = 2 \times 3^2 \)
- Apply the square root: \( \sqrt{18} = \sqrt{2 \times 3^2} = 3\sqrt{2} \)
-
Ignoring the Coefficient:
Another mistake is forgetting to multiply the coefficient outside the square root. For instance, simplifying \( 3\sqrt{18} \) without considering the 3 outside the root.
To simplify correctly:
- Simplify \( \sqrt{18} \) as \( 3\sqrt{2} \)
- Multiply by the coefficient: \( 3 \times 3\sqrt{2} = 9\sqrt{2} \)
-
Misapplying the Order of Operations:
Students sometimes neglect the order of operations, especially when multiple terms are involved. For example, simplifying \( 3 + \sqrt{18} \) incorrectly as \( \sqrt{21} \).
To avoid this:
- Separate the terms: \( 3 + \sqrt{18} \)
- Simplify \( \sqrt{18} \) first: \( 3 + 3\sqrt{2} \)
- Combine the terms: \( 3 + 3\sqrt{2} \)
-
Not Rationalizing the Denominator:
When dividing by a square root, students might leave the square root in the denominator, which is often not simplified fully. For example, leaving \( \frac{3}{\sqrt{2}} \) as it is.
To rationalize the denominator:
- Multiply numerator and denominator by \( \sqrt{2} \):
- \( \frac{3}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{3\sqrt{2}}{2} \)
-
Forgetting Both Positive and Negative Roots:
While solving equations involving square roots, students might forget that both positive and negative roots are valid solutions. For example, solving \( x^2 = 18 \) and only considering \( \sqrt{18} \).
To avoid this, remember:
- \( x^2 = 18 \) implies \( x = \pm \sqrt{18} \)
- Simplify to \( x = \pm 3\sqrt{2} \)
Additional Resources and Further Reading
To deepen your understanding of simplifying square roots and their applications, here are some valuable resources and further reading materials:
-
Math Is Fun - Simplifying Square Roots: This resource offers a detailed explanation of how to simplify square roots, including step-by-step examples. It also covers the product rule and provides exercises for practice.
-
Symbolab - Study Guide on Simplifying Square Roots: Symbolab provides a comprehensive guide on the product and quotient rules for simplifying square roots. The guide includes worked examples and practice problems to test your understanding.
-
Socratic - Simplifying Radicals: Socratic's Q&A platform is excellent for specific questions about simplifying radicals. It includes various examples and detailed explanations on how to handle different types of radical expressions.
-
Mathway - Algebra Examples: Mathway offers step-by-step solutions for algebra problems, including simplifying square roots. This resource is beneficial for visual learners who benefit from seeing each step in the process.
These resources should provide you with a robust understanding of simplifying square roots and their various applications. Happy learning!
Conclusion and Summary
In this comprehensive guide, we have explored the concept of square roots, focusing specifically on the calculation and simplification of \(3 \sqrt{18}\). Here are the key points to take away:
- We began with an introduction to square roots, explaining their fundamental principles and the importance of understanding them.
- We delved into the basics of square root calculation, covering methods such as the prime factorization method which helps simplify square roots effectively.
- The step-by-step calculation of \(3 \sqrt{18}\) was demonstrated, illustrating the process and highlighting the significance of simplification.
- We emphasized the mathematical properties of square roots and how they apply in various contexts.
- A series of examples and practice problems were provided to reinforce learning and offer hands-on experience with square root calculations.
- We discussed the practical applications of square roots in real-life scenarios, showing their relevance beyond mathematical theory.
- Common mistakes in calculating and simplifying square roots were identified, along with strategies to avoid them.
- Additional resources and further reading materials were recommended for those interested in deepening their understanding of square roots.
In summary, mastering the concept of square roots, especially in expressions like \(3 \sqrt{18}\), equips us with valuable mathematical tools that are applicable in various fields such as science, engineering, and everyday problem-solving. Continued practice and application of these concepts will further enhance your proficiency and confidence in handling square root calculations.
Cách Đơn Giản Hóa Căn Bậc Hai của 18: Sqrt(18)
READ MORE:
3/√(18) = ? Nhiều người không biết tại sao điều này SAI!






