Topic what is the square root of 1/16: Welcome to our comprehensive guide on the square root of 1/16. Whether you're new to square roots or looking to deepen your understanding, this article will walk you through step-by-step calculations, explore visual representations, and discuss real-life applications. Dive into the world of mathematical properties, common mistakes, and advanced topics to master this fundamental concept.
Table of Content
- Understanding the Square Root of 1/16
- Introduction to Square Roots
- Understanding the Square Root of Fractions
- Step-by-Step Calculation of the Square Root of 1/16
- Mathematical Properties of the Square Root
- Visual Representation of the Square Root of 1/16
- Applications of Square Roots in Real Life
- Frequently Asked Questions about Square Roots
- Common Mistakes When Calculating Square Roots
- Advanced Topics in Square Roots
- Conclusion and Summary
- YOUTUBE: Video này giải thích cách tính căn bậc hai của 1/16 và tầm quan trọng của nó trong toán học.
Understanding the Square Root of 1/16
The square root of a number is a value that, when multiplied by itself, gives the original number. To find the square root of 1/16, we can use the following steps:
Step-by-Step Calculation
- Identify the number to find the square root of: \( \frac{1}{16} \).
- Recognize that the square root function can be applied to both the numerator and the denominator separately in a fraction.
- Calculate the square root of the numerator: \( \sqrt{1} = 1 \).
- Calculate the square root of the denominator: \( \sqrt{16} = 4 \).
Thus, the square root of \( \frac{1}{16} \) is:
\[
\sqrt{\frac{1}{16}} = \frac{\sqrt{1}}{\sqrt{16}} = \frac{1}{4}
\]
Therefore, the square root of \( \frac{1}{16} \) is \( \frac{1}{4} \) or 0.25.
Visual Representation
To better understand, here's a visual representation:
| Original Fraction | Square Root |
| \( \frac{1}{16} \) | \( \frac{1}{4} \) |
In conclusion, the square root of \( \frac{1}{16} \) is \( \frac{1}{4} \). This can be written as a decimal value of 0.25.

READ MORE:
Introduction to Square Roots
Square roots are a fundamental concept in mathematics that involve finding a number which, when multiplied by itself, gives a specified number. For the fraction \( \frac{1}{16} \), the square root is calculated as follows:
- Recognize that the square root of \( \frac{1}{16} \) can be expressed as \( \sqrt{\frac{1}{16}} \).
- To simplify, note that \( \sqrt{\frac{1}{16}} = \frac{\sqrt{1}}{\sqrt{16}} = \frac{1}{4} \), since \( \sqrt{1} = 1 \) and \( \sqrt{16} = 4 \).
- Therefore, \( \sqrt{\frac{1}{16}} = \frac{1}{4} \).
Understanding square roots is crucial for various mathematical applications, including geometry, physics, and engineering.
Understanding the Square Root of Fractions
Calculating the square root of a fraction may initially seem challenging, but it can be simplified by understanding a few key principles.
The square root of a fraction follows the rule:
\[ \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \]
To understand this better, let's break down the steps involved in calculating the square root of \(\frac{1}{16}\).
- Identify the numerator and the denominator: In the fraction \(\frac{1}{16}\), 1 is the numerator and 16 is the denominator.
- Find the square root of the numerator: The square root of 1 is 1.
- Find the square root of the denominator: The square root of 16 is 4.
- Express the square root of the fraction: Combine the results from steps 2 and 3:
\[ \sqrt{\frac{1}{16}} = \frac{\sqrt{1}}{\sqrt{16}} = \frac{1}{4} \]
Thus, the square root of \(\frac{1}{16}\) is \(\frac{1}{4}\).
This method can be applied to any fraction, simplifying the process of finding square roots of fractions in general.
It's also useful to remember some basic properties of square roots of fractions:
- Non-negative Results: The square root of a positive fraction is always a positive number.
- Inverse Relationship: The square root of a fraction less than 1 is greater than the original fraction, while the square root of a fraction greater than 1 is less than the original fraction.
- Product Rule: The square root of a product of fractions is the product of their square roots:
\[ \sqrt{\frac{a}{b} \cdot \frac{c}{d}} = \sqrt{\frac{a \cdot c}{b \cdot d}} = \frac{\sqrt{a} \cdot \sqrt{c}}{\sqrt{b} \cdot \sqrt{d}} \]
By understanding and applying these principles, you can effectively calculate the square root of any fraction with confidence.
Step-by-Step Calculation of the Square Root of 1/16
Calculating the square root of a fraction involves finding the square root of the numerator and the square root of the denominator separately. Let's go through this process step by step.
-
Identify the Numerator and Denominator:
For the fraction , the numerator is 1 and the denominator is 16.
-
Find the Square Root of the Numerator:
The square root of 1 is 1, since .
-
Find the Square Root of the Denominator:
The square root of 16 is 4, since .
-
Form the Fraction:
Now that we have the square root of the numerator and the square root of the denominator, we can form the fraction:
-
Simplify if Necessary:
In this case, the fraction is already in its simplest form.
-
Verify the Result:
To ensure our result is correct, we can square and check if we get back to the original fraction:
Thus, the square root of is .
Mathematical Properties of the Square Root
The square root function has several interesting mathematical properties that make it a fundamental concept in various branches of mathematics. Here are some key properties:
- Non-negativity: For any non-negative number \( x \), the square root is also non-negative. Formally, if \( x \geq 0 \), then \( \sqrt{x} \geq 0 \).
- Product Rule: The square root of a product is the product of the square roots. Mathematically, this is expressed as: \[ \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \] for any non-negative numbers \( a \) and \( b \).
- Quotient Rule: The square root of a quotient is the quotient of the square roots: \[ \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \] for any non-negative numbers \( a \) and \( b \), with \( b \neq 0 \).
- Square Root of a Power: The square root of a number can be expressed as an exponent. Specifically, \[ \sqrt{x} = x^{1/2} \quad \text{or} \quad \sqrt{x} = x^{0.5} \] for any non-negative number \( x \).
- Even and Odd Digits: If a number is a perfect square, then its last digit must be 0, 1, 4, 5, 6, or 9. Conversely, a number ending in 2, 3, 7, or 8 cannot be a perfect square.
- Rational and Irrational Roots: The square root of a perfect square is a rational number, while the square root of a non-perfect square is an irrational number.
- Sum of Odd Numbers: The square of a natural number \( n \) is equal to the sum of the first \( n \) odd numbers. For example, \[ 1 + 3 + 5 + 7 + 9 = 25 = 5^2 \]
- Square Roots of Negative Numbers: The square root of a negative number is not a real number but an imaginary number. It is expressed using the imaginary unit \( i \), where \( i = \sqrt{-1} \). For example, \[ \sqrt{-4} = 2i \]
These properties are essential in understanding the behavior and application of square roots in various mathematical contexts.
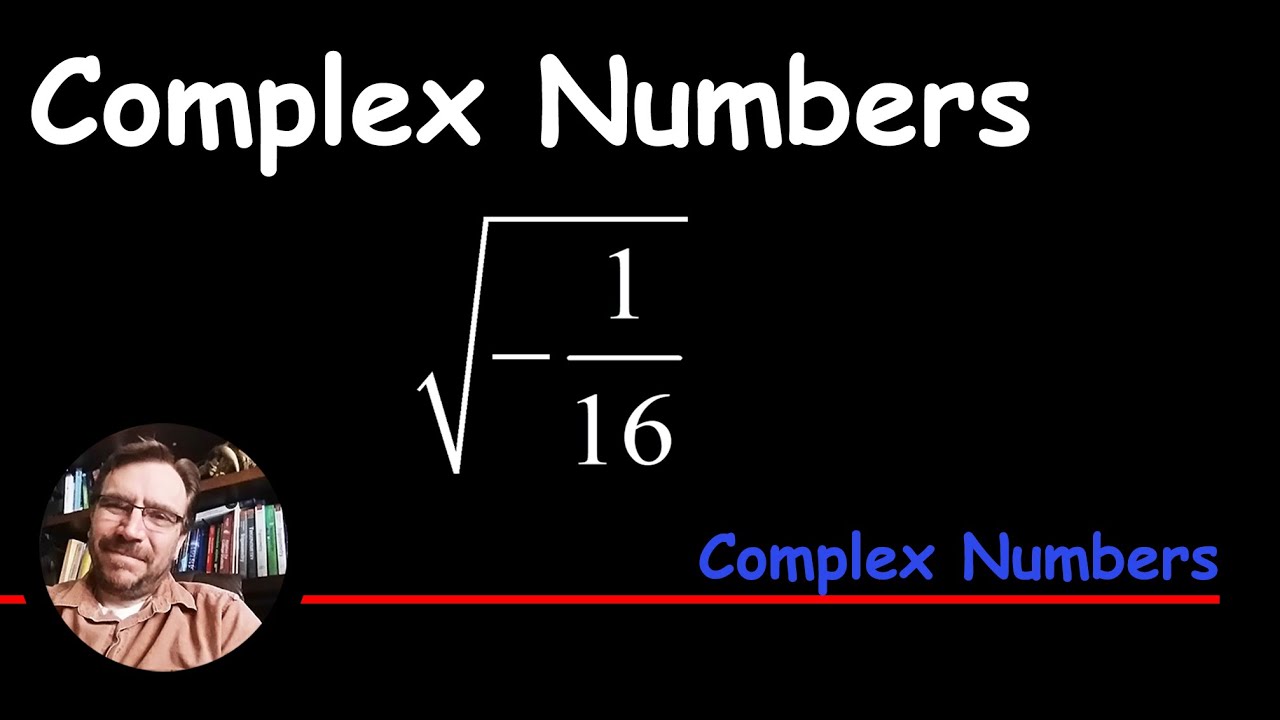
Visual Representation of the Square Root of 1/16
The square root of 1/16 can be visually represented in several ways to help with understanding its value and properties. Here are some visual methods to illustrate the square root of 1/16:
Number Line Representation
One way to represent the square root of 1/16 is on a number line. Since the square root of 1/16 is 1/4, you can show this by marking the points 0, 1/4, 1/2, 3/4, and 1 on the number line:
- 0
- 1/4
- 1/2
- 3/4
- 1
The point at 1/4 represents the square root of 1/16.
Geometric Representation
Another way to visualize the square root of 1/16 is through geometry. You can draw a square with an area of 1/16 and show that each side of the square is 1/4. This helps illustrate the relationship between the area of a square and its side length:
- Draw a square with area 1/16.
- Each side of the square will be 1/4, since (1/4) * (1/4) = 1/16.
This geometric representation helps in understanding that the square root is the length of a side of a square with a given area.
Graphical Representation
You can also use a graph to show the relationship between the square root function and the value 1/16. Plot the function \(y = \sqrt{x}\) and highlight the point where \(x = 1/16\):
The corresponding \(y\)-value will be 1/4, illustrating that \(\sqrt{1/16} = 1/4\).
Here is the graph of \(y = \sqrt{x}\) with the point (1/16, 1/4) highlighted:
- Graph of \(y = \sqrt{x}\)
- Highlight the point (1/16, 1/4)
This graphical approach shows the square root function in action and provides a clear visual of the square root of 1/16.
Table Representation
Creating a table can also help visualize the square roots of different fractions, including 1/16:
| Fraction | Square Root |
|---|---|
| 1/4 | 1/2 |
| 1/9 | 1/3 |
| 1/16 | 1/4 |
| 1/25 | 1/5 |
This table helps to see the pattern and relationship between fractions and their square roots.
Applications of Square Roots in Real Life
Square roots play a vital role in various real-life applications across multiple disciplines. Here are some of the key areas where square roots are utilized:
- Finance: In finance, square roots are used to calculate stock market volatility. This metric helps investors assess the risk associated with a particular investment by determining the standard deviation of stock returns.
- Engineering and Architecture: Square roots are essential in calculating the natural frequencies of structures like bridges and buildings. These frequencies help engineers predict how structures will respond to environmental stresses like wind or traffic.
- Science: In scientific research, square roots are used in various calculations, such as determining the intensity of sound waves or the velocity of moving objects. These calculations aid in understanding natural phenomena and developing new technologies.
- Statistics: Square roots are used to compute standard deviation, which measures how data points deviate from the mean. This is crucial in data analysis for making informed decisions based on statistical results.
- Geometry: Square roots are fundamental in geometry, especially in the Pythagorean theorem, which is used to calculate distances and solve problems involving right triangles.
- Computer Science: In computer programming, square roots are used in encryption algorithms, image processing, and game physics. These applications ensure data security, enhance visual effects, and create realistic game environments.
- Cryptography: Square roots are used in generating digital signatures and key exchange systems, which are crucial for secure communication and data authentication.
- Navigation: Pilots and navigators use square roots to calculate distances between points on a map or globe and estimate bearings or directions for travel.
- Electrical Engineering: Square roots are used to calculate power, voltage, and current in electrical circuits. These calculations are critical for designing efficient electrical systems.
- Cooking: Recipes often require adjustments in ingredient quantities based on scaling factors, where square roots help maintain the right balance of flavors.
- Photography: The aperture of a camera lens is related to the square of the f-number, affecting the amount of light that enters the camera and thus the exposure of the photograph.
- Computer Graphics: In 2D and 3D graphics, square roots are used to calculate distances between points and lengths of vectors, essential for rendering images accurately.
- Telecommunication: Signal strength in wireless communication decreases with distance, following the inverse square law, which involves square root calculations.
Frequently Asked Questions about Square Roots
Square roots can often lead to questions due to their unique properties and applications. Here are some frequently asked questions about square roots:
- What is the square root of 1/16?
The square root of \(\frac{1}{16}\) is \(\frac{1}{4}\). This is because \(\left(\frac{1}{4}\right)^2 = \frac{1}{16}\).
- How do you simplify the square root of a fraction?
To simplify the square root of a fraction, you take the square root of the numerator and the square root of the denominator separately. For example, \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\).
- Can square roots be negative?
By definition, the principal square root is always non-negative. However, every positive number has two square roots: a positive and a negative one. For instance, both 2 and -2 are square roots of 4.
- What are perfect squares?
Perfect squares are numbers that are the square of an integer. Examples include 1, 4, 9, 16, 25, etc. For instance, \(16 = 4^2\) and \(9 = 3^2\).
- Why are square roots important?
Square roots are important in various fields such as geometry, algebra, and physics. They are used in solving quadratic equations, determining distances in coordinate systems, and analyzing wave functions in physics.
Common Mistakes When Calculating Square Roots
Calculating square roots can be tricky, and there are several common mistakes that people often make. Being aware of these errors can help ensure accuracy in your calculations. Here are some of the most frequent mistakes:
- Forgetting the Negative Root: When solving equations involving square roots, it's essential to remember that both positive and negative roots can be solutions. For example, the square root of 16 is both 4 and -4, since \(4^2 = 16\) and \((-4)^2 = 16\).
- Misinterpreting the Square Root Symbol: The symbol \( \sqrt{} \) represents the principal (non-negative) square root. However, in equations, both roots should be considered. Ensure you're not mistakenly assuming only the positive root in cases where both are relevant.
- Incorrect Application of Properties: Students sometimes assume properties that don't apply to square roots. For instance, \(\sqrt{a + b} \neq \sqrt{a} + \sqrt{b}\). This incorrect assumption can lead to significant errors in calculations.
- Errors in Simplifying Radical Expressions: Simplifying square roots requires careful attention to prime factorization. Failing to correctly simplify the radicand can result in incorrect answers. For example, \(\sqrt{50}\) should be simplified to \(5\sqrt{2}\), not approximated incorrectly.
- Misplacing Decimal Points: When dealing with square roots of non-perfect squares, misplacing the decimal point can lead to incorrect results. Accurate placement of the decimal ensures precision in the final answer.
- Rounding Errors: Over-rounding intermediate steps can accumulate errors. It's best to keep as many decimal places as possible during calculations and only round the final result.
- Incorrect Use of Calculators: Relying on calculators without understanding the process can lead to errors. Make sure you input the correct numbers and functions, and double-check the results manually when possible.
- Assuming Linear Properties: It's incorrect to assume linearity in square root operations. For example, \((x + y)^2 \neq x^2 + y^2\). This mistake often leads to incorrect simplifications and results.
By being mindful of these common mistakes, you can improve your accuracy when calculating square roots and develop a stronger understanding of mathematical principles.

Advanced Topics in Square Roots
Square roots are a fundamental concept in mathematics, often extending beyond basic calculations to more complex and advanced topics. Here, we explore some advanced topics related to square roots, including irrational numbers, complex numbers, and the application of square roots in various fields.
-
Irrational Numbers:
Not all square roots result in rational numbers. For example, while , the square root of 2 () is an irrational number. An irrational number cannot be expressed as a simple fraction and has a non-repeating, non-terminating decimal expansion.
-
Complex Numbers:
Square roots of negative numbers involve complex numbers. The square root of -1 is denoted as , the imaginary unit. Therefore, the square root of any negative number can be expressed in terms of . For instance, .
-
Applications in Real Life:
Square roots are used in various real-life applications such as in physics for calculating root mean square velocity, in statistics for standard deviation, and in finance for determining volatility of stocks. The Pythagorean theorem, which involves square roots, is crucial in architecture and engineering.
-
Computational Methods:
Advanced computational methods for finding square roots include the Newton-Raphson method, which iteratively improves the approximation of a square root, and algorithms used in computer science for efficient calculations.
Conclusion and Summary
In this guide, we explored the concept of square roots with a focus on the fraction 1/16. Understanding how to calculate and simplify square roots is essential in mathematics, particularly in algebra and calculus.
The square root of 1/16 is calculated as follows:
- First, express the fraction under the square root: \(\sqrt{\frac{1}{16}}\).
- Next, separate the square root of the numerator and the denominator: \(\frac{\sqrt{1}}{\sqrt{16}}\).
- Simplify both the square root of 1 and the square root of 16: \(\frac{1}{4}\).
This calculation shows that the square root of 1/16 is \(\frac{1}{4}\) or 0.25.
Throughout this guide, we also covered advanced topics such as the properties of square roots, how to handle square roots in fractions, and the implications of these calculations in various mathematical contexts.
Key takeaways include:
- The square root of a fraction can be simplified by taking the square roots of the numerator and the denominator separately.
- Knowing how to simplify fractions under square roots is useful for solving algebraic equations and understanding higher-level math concepts.
- Practicing these calculations helps build a solid foundation in algebra and prepares you for more complex mathematical operations.
By mastering these skills, you can confidently tackle square root problems and apply these techniques in both academic and real-world scenarios.
We hope this guide has been helpful in enhancing your understanding of square roots and their applications. Continue practicing and exploring more advanced mathematical concepts to further your knowledge and proficiency.
Video này giải thích cách tính căn bậc hai của 1/16 và tầm quan trọng của nó trong toán học.
Căn bậc hai của 1/16 | Root(1/16)
READ MORE:
Bình phương của một phân số âm √-1/16
Bình phương của một phân số âm √-1/16