Is the Square Root of 18 a Rational Number? Discover the Truth!

The square root of 18 is an interesting number to explore in terms of its rationality.

Definition of Rational and Irrational Numbers

To determine if the square root of 18 is a rational number, we first need to understand the definitions:

• Rational Numbers: Numbers that can be expressed as the quotient of two integers, where the denominator is not zero. Examples include 1/2, 3, and -4.
• Irrational Numbers: Numbers that cannot be expressed as a simple fraction. Their decimal expansions are non-repeating and non-terminating. Examples include π and √2.

Evaluating √18

The square root of 18 can be simplified as follows:

\[
\sqrt{18} = \sqrt{9 \times 2} = \sqrt{9} \times \sqrt{2} = 3\sqrt{2}
\]

Since √2 is known to be an irrational number, multiplying it by 3 (a rational number) still results in an irrational number.

Conclusion

Based on the above evaluation, we can conclude that the square root of 18, or 3√2, is an irrational number.

Additional Insights

Here are some additional points to consider:

1. Irrational numbers cannot be precisely expressed as fractions.
2. The decimal expansion of √18 is approximately 4.242640687, and it is non-repeating and non-terminating.
3. Understanding the properties of square roots helps in various fields such as mathematics, engineering, and science.

Rational numbers are those that can be expressed as a fraction of two integers, where the denominator is not zero. They include integers and fractions like \( \frac{1}{2} \), \( \frac{3}{4} \), and \( -7 \).

Irrational numbers, on the other hand, cannot be expressed as fractions of integers. They have non-repeating, non-terminating decimal representations. Examples include \( \sqrt{2} \), \( \pi \), and \( e \).

The distinction between rational and irrational numbers is crucial in mathematics, affecting various fields such as number theory, algebra, and geometry.

The square root of 18, denoted as \( \sqrt{18} \), is an irrational number. To understand why, let's explore its properties:

1. Prime Factorization of 18:

   18	=	2 × 9
   	=	2 × 3 × 3

   Therefore, \( 18 = 2 \times 3^2 \).

2. Implications of Prime Factorization:

   The prime factorization of 18 shows that it contains the prime number 3 raised to a power greater than 1, indicating that \( \sqrt{18} \) cannot be expressed as a fraction of two integers. This property categorizes \( \sqrt{18} \) as an irrational number.

3. Decimal Approximation:

   Calculating \( \sqrt{18} \) approximately gives us \( \sqrt{18} \approx 4.24 \). The decimal representation of \( \sqrt{18} \) is non-repeating and non-terminating, further confirming its irrationality.

To determine whether \( \sqrt{18} \) is a rational number, we begin with its prime factorization:

Thus, \( 18 = 2 \times 3^2 \). This prime factorization shows that 18 contains the prime number 3 raised to a power greater than 1, which implies that \( \sqrt{18} \) is an irrational number.

The square root of 18 is considered irrational because it cannot be expressed as a simple fraction. To understand why √18 is irrational, we can look at its prime factorization and decimal expansion.

Prime Factorization Method

First, let's break down 18 into its prime factors:

• 18 = 2 × 3 × 3
• This can be written as 18 = 2 × 3²

Taking the square root of both sides:

\(\sqrt{18} = \sqrt{2 \times 3^2}\)

Simplifying this, we get:

\(\sqrt{18} = 3\sqrt{2}\)

Since the square root of 2 (√2) is known to be an irrational number, multiplying it by 3 does not change this property. Thus, \(3\sqrt{2}\) is also irrational.

Decimal Expansion

The square root of 18 in decimal form is approximately 4.242640687. This decimal neither terminates nor repeats, which is a key characteristic of irrational numbers.

Properties of Irrational Numbers

• They cannot be expressed as a ratio of two integers.
• Their decimal expansions are non-terminating and non-repeating.
• Examples include √2, π, and e.

Conclusion

Because √18 simplifies to \(3\sqrt{2}\) and √2 is irrational, √18 inherits this property. The non-repeating, non-terminating nature of its decimal form further confirms its irrationality.

To prove that the square root of 18 is irrational, we can use a proof by contradiction. This involves assuming the opposite of what we want to prove and showing that this leads to a contradiction.

1. Assume that √18 is a rational number. This means it can be expressed as a fraction of two integers \( \frac{a}{b} \), where \( a \) and \( b \) are coprime (i.e., they have no common factors other than 1) and \( b \neq 0 \).
2. Therefore, we can write:

   
   \[ \sqrt{18} = \frac{a}{b} \]
   Squaring both sides, we get:
   \[ 18 = \frac{a^2}{b^2} \]
   Multiplying both sides by \( b^2 \), we get:
   \[ 18b^2 = a^2 \]

3. This implies that \( a^2 \) is divisible by 18. Since 18 is \( 2 \times 3^2 \), \( a^2 \) must be divisible by both 2 and 9.
4. Thus, \( a \) itself must be divisible by 3 (since \( 3^2 \) divides \( a^2 \)). Let \( a = 3k \) for some integer \( k \).
5. Substituting \( a = 3k \) back into the equation \( 18b^2 = a^2 \), we get:

   
   \[ 18b^2 = (3k)^2 \]
   \[ 18b^2 = 9k^2 \]

6. Dividing both sides by 9, we get:

   
   \[ 2b^2 = k^2 \]

7. This means \( k^2 \) is even, and hence \( k \) must be even (since the square of an odd number is odd).
8. Let \( k = 2m \) for some integer \( m \). Substituting \( k = 2m \) back into \( 2b^2 = k^2 \), we get:

   
   \[ 2b^2 = (2m)^2 \]
   \[ 2b^2 = 4m^2 \]
   Dividing both sides by 2, we get:
   \[ b^2 = 2m^2 \]

9. This means \( b^2 \) is even, and hence \( b \) must be even.
10. Now we have shown that both \( a \) and \( b \) are even, which contradicts the assumption that \( a \) and \( b \) are coprime.
11. Since our initial assumption that \( \sqrt{18} \) is rational leads to a contradiction, we conclude that \( \sqrt{18} \) must be irrational.

Irrational numbers have unique properties that distinguish them from rational numbers. Understanding these properties helps us comprehend why numbers like √18 fall into this category.

• Non-repeating and Non-terminating Decimals: Irrational numbers cannot be expressed as exact fractions. Their decimal expansions go on forever without repeating patterns. For example, the decimal expansion of √18 is approximately 4.24264068712, which continues indefinitely without repetition.
• Not Expressible as Fractions: Irrational numbers cannot be written as a simple fraction \( \frac{p}{q} \), where \( p \) and \( q \) are integers and \( q \neq 0 \). This is a defining characteristic of irrational numbers, differentiating them from rational numbers which can always be expressed as such fractions.
• Square Roots of Non-perfect Squares: The square roots of numbers that are not perfect squares are always irrational. Since 18 is not a perfect square, its square root, √18, is irrational. This means there is no pair of integers whose ratio equals √18.
• Non-repeating Decimal Expansion Example: Let’s look at √18 more closely. Using the long division method, we can find the decimal expansion up to several decimal places, confirming its non-repeating, non-terminating nature.
• Unique Representation on the Number Line: While irrational numbers are found on the number line, they cannot be pinpointed precisely with simple fractions or decimals. They are real numbers that fill the gaps between rational numbers.

These properties highlight the fundamental differences between rational and irrational numbers. Recognizing these distinctions helps in various mathematical and real-world applications.

The decimal expansion of the square root of 18, denoted as \( \sqrt{18} \), is non-terminating and non-repeating, indicating that it is an irrational number. Here is a detailed breakdown of how to find the decimal expansion:

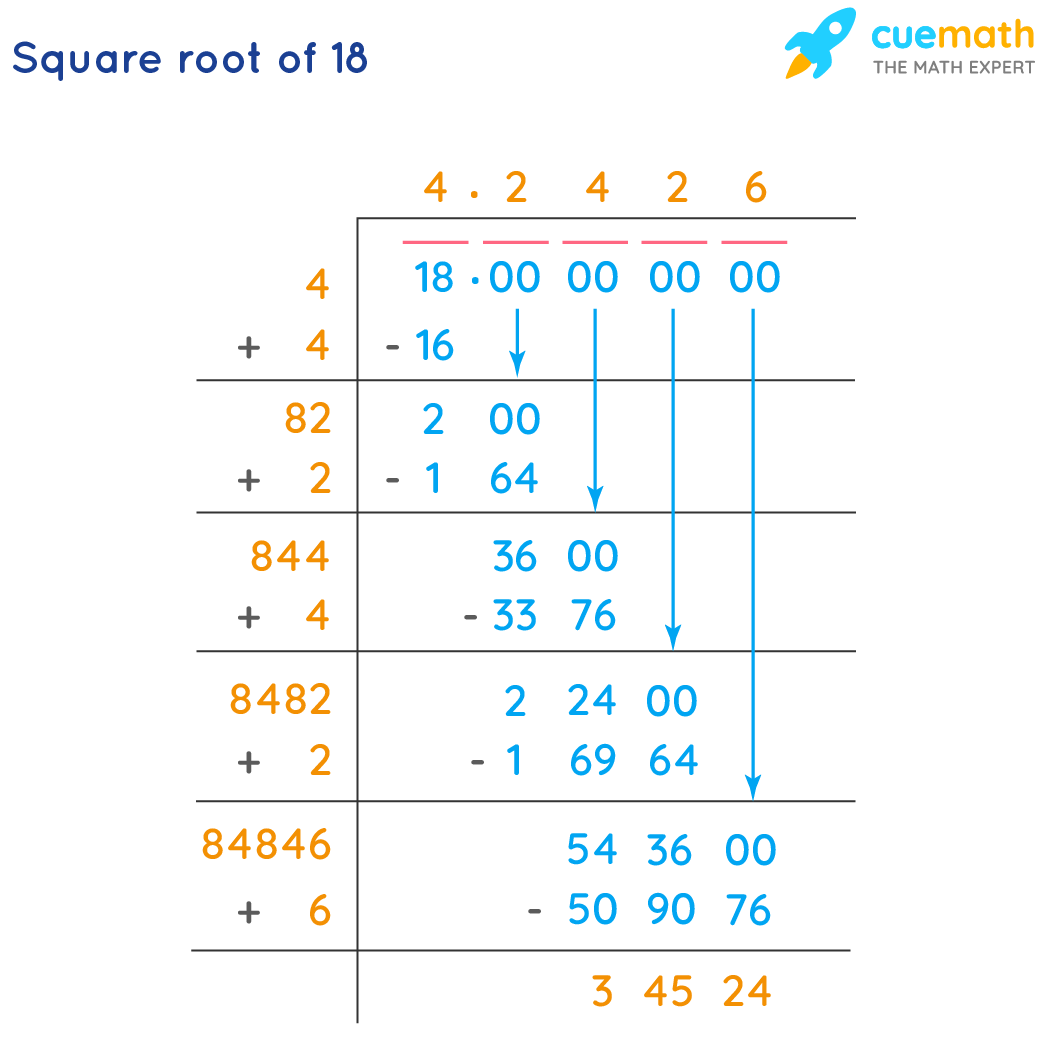
Using the Long Division Method

The long division method is one of the most reliable techniques to find the decimal expansion of \( \sqrt{18} \). Below are the steps:

1. Write the number 18 as 18.000000 to facilitate the division process.
2. Group the digits in pairs from the decimal point. For 18, we treat it as "18.00 00 00 00".
3. Find the largest number whose square is less than or equal to 18. This number is 4, since \(4^2 = 16\). Place 4 as the first digit of the quotient.
4. Subtract 16 from 18 to get a remainder of 2. Bring down the next pair of zeros to make it 200.
5. Double the quotient obtained so far (4) to get 8. Determine the next digit (X) such that \(8X \times X \leq 200\). The digit X is 2, because \(82 \times 2 = 164\).
6. Subtract 164 from 200 to get 36. Bring down the next pair of zeros to get 3600.
7. Double the current quotient (42) to get 84. Determine the next digit (Y) such that \(84Y \times Y \leq 3600\). The digit Y is 4, because \(844 \times 4 = 3376\).
8. Continue this process to achieve the desired level of precision. The decimal expansion begins as 4.2426...

Approximation Method

Another method to approximate \( \sqrt{18} \) involves identifying the perfect squares closest to 18:

1. Since \(18\) lies between \(4^2 = 16\) and \(5^2 = 25\), \( \sqrt{18} \) is between 4 and 5.
2. Using interpolation, we refine this to 4.2 since \((18 - 16)/(25 - 16) = 2/9 \approx 0.22\).
3. Thus, \( \sqrt{18} \approx 4.22 \), although more precise calculations yield 4.2426...

In summary, the decimal expansion of \( \sqrt{18} \) is approximately 4.2426, and it continues indefinitely without repeating.

The square root of 18, denoted as \( \sqrt{18} \), is an irrational number. Despite its irrationality, it has practical applications in various fields. Here are some examples:

• Geometry: In geometry, \( \sqrt{18} \) is often encountered when dealing with right triangles. For example, in a right triangle where the legs are of lengths 3 and 3√2, the hypotenuse is \( \sqrt{18} \).
• Engineering: Engineers may use \( \sqrt{18} \) in calculations involving physical dimensions that require precise measurements. For instance, calculating the diagonal of a rectangular object with sides 3 units and 3√2 units.
• Physics: In physics, the square root of 18 can be found in wave mechanics and other applications requiring precise numerical solutions.
• Computer Science: Algorithms that involve geometric computations may require the use of \( \sqrt{18} \) for calculating distances and optimizing solutions.

To illustrate how \( \sqrt{18} \) can be approximated in calculations, let's consider the following steps:

1. Recognize that \( \sqrt{18} \) simplifies to \( 3\sqrt{2} \).
2. Since \( \sqrt{2} \) is approximately 1.414, \( \sqrt{18} \approx 3 \times 1.414 = 4.242 \).
3. This approximation is useful in practical calculations where an exact value is not required.

Despite being an irrational number, \( \sqrt{18} \) is essential in solving real-world problems that involve measurements, optimizations, and precise calculations.