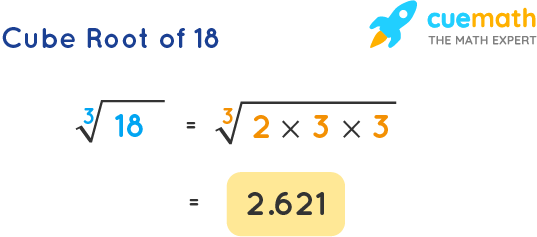
Topic is the square root of 1 a rational number: Is the square root of 1 a rational number? This intriguing question has a simple yet fascinating answer. Explore the mathematical properties of rational and irrational numbers, and learn why the square root of 1 fits perfectly into the category of rational numbers. Dive in to enhance your understanding of this fundamental concept.
Table of Content
- Is the Square Root of 1 a Rational Number?
- Introduction to Rational Numbers
- Definition of Rational Numbers
- Characteristics of Rational Numbers
- Examples of Rational Numbers
- Definition of Irrational Numbers
- Properties of Square Roots
- Calculation of Square Root of 1
- Mathematical Representation of Square Roots
- Is 1 a Rational Number?
- Is -1 a Rational Number?
- Rationality of Square Root of 1
- Examples of Rational and Irrational Square Roots
- Conclusion on Rationality of Square Root of 1
- YOUTUBE: Hướng dẫn cách đơn giản hóa căn bậc hai của một số hữu tỉ để thu hút người xem. Video phù hợp với bài viết 'căn bậc hai của 1 có phải là số hữu tỉ không?'
Is the Square Root of 1 a Rational Number?
The question of whether the square root of 1 is a rational number can be answered affirmatively. Let's delve into the details:
Understanding Rational Numbers
A rational number is defined as any number that can be expressed as the quotient or fraction p/q of two integers, where p and q are integers and q is not zero. Examples of rational numbers include:
- 1/2
- -3/4
- 5 (which can be written as 5/1)
Square Root of 1
The square root of a number x is a value that, when multiplied by itself, gives x. Mathematically, the square root of 1 is denoted as:
\[
\sqrt{1} = 1
\]
or
\[
\sqrt{1} = -1
\]
Rationality of the Square Roots
Both 1 and -1 are integers. Since integers can be expressed as the quotient of themselves and 1, they are also rational numbers. For instance:
- 1 can be written as 1/1
- -1 can be written as -1/1
Conclusion
Based on the definitions and properties of rational numbers, we can conclude that the square roots of 1, both 1 and -1, are rational numbers.

READ MORE:
Introduction to Rational Numbers
Rational numbers are a fundamental concept in mathematics, representing any number that can be expressed as the quotient or fraction p/q, where p and q are integers and q is not zero. To better understand rational numbers, let's explore their properties and some examples:
Properties of Rational Numbers
- Can be written in the form p/q where p and q are integers, and q ≠ 0.
- Includes both positive and negative numbers.
- Includes zero (since 0 can be written as 0/1).
- Decimal representation is either terminating or repeating.
Examples of Rational Numbers
- 1/2 - A positive rational number.
- -3/4 - A negative rational number.
- 5 - An integer (can be written as 5/1).
- 0 - Zero (can be written as 0/1).
- 2.5 - A decimal number (can be written as 5/2).
Contrasting Rational and Irrational Numbers
While rational numbers can be expressed as fractions, irrational numbers cannot be. Irrational numbers have non-terminating, non-repeating decimal expansions. Examples include:
- \(\pi\)
- \(\sqrt{2}\)
- \(e\) (Euler's number)
Understanding the distinction between rational and irrational numbers is crucial for grasping more advanced mathematical concepts. Rational numbers are not only foundational but also versatile in various mathematical applications.
Definition of Rational Numbers
A rational number is any number that can be expressed as the quotient or fraction \(\frac{p}{q}\) of two integers, where p (the numerator) and q (the denominator) are integers, and q is not zero.
To better understand rational numbers, let's break down the definition into key characteristics:
- Quotient of Integers: A rational number is represented as
\(\frac{p}{q}\), where bothpandqare integers. - Non-zero Denominator: The integer
q(denominator) must not be zero, because division by zero is undefined. - Finite or Repeating Decimals: Rational numbers can be expressed as decimals that either terminate (e.g., 0.5, 0.75) or repeat periodically (e.g., 0.333..., 1.666...).
To illustrate, here are some examples of rational numbers:
\(\frac{1}{2}\)(which equals 0.5)\(\frac{3}{4}\)(which equals 0.75)\(\frac{2}{3}\)(which equals 0.666...)- 5 (which can be written as
\(\frac{5}{1}\)) - -2 (which can be written as
\(\frac{-2}{1}\))
Thus, rational numbers form a significant part of the number system, encompassing integers, fractions, and finite or repeating decimals.
Characteristics of Rational Numbers
Rational numbers are a subset of real numbers characterized by specific properties. Here are the main characteristics:
- Form: A rational number can be expressed as the quotient or fraction \(\frac{p}{q}\), where \(p\) and \(q\) are integers and \(q \neq 0\).
- Terminating or Repeating Decimals: Rational numbers can be represented as either terminating decimals (e.g., \(0.5 = \frac{1}{2}\)) or repeating decimals (e.g., \(0.333\ldots = \frac{1}{3}\)).
- Closed Under Arithmetic Operations: The set of rational numbers is closed under addition, subtraction, multiplication, and division (except by zero). This means that the result of these operations on any two rational numbers will also be a rational number. For example:
- \( \frac{1}{2} + \frac{1}{3} = \frac{3}{6} + \frac{2}{6} = \frac{5}{6} \)
- \( \frac{2}{3} \times \frac{3}{4} = \frac{6}{12} = \frac{1}{2} \)
- Additive and Multiplicative Inverses: Every rational number has an additive inverse and, if non-zero, a multiplicative inverse. For any rational number \(\frac{a}{b}\):
- Additive inverse: \(-\frac{a}{b}\)
- Multiplicative inverse: \(\frac{b}{a}\)
- Examples: Common examples of rational numbers include:
- Integers: \( -2, 0, 3 \) (since they can be expressed as fractions like \(\frac{-2}{1}, \frac{0}{1}, \frac{3}{1}\))
- Simple fractions: \(\frac{4}{5}, \frac{-7}{3}\)
- Terminating decimals: \(0.25 = \frac{1}{4}, 1.75 = \frac{7}{4}\)
- Repeating decimals: \(0.666\ldots = \frac{2}{3}, 1.333\ldots = \frac{4}{3}\)
Understanding these characteristics helps in identifying and working with rational numbers in various mathematical contexts.
Examples of Rational Numbers
Rational numbers are numbers that can be expressed as the quotient or fraction p/q of two integers, where p and q are integers and q is not zero. Here are some common examples of rational numbers:
- Integers: All integers are rational numbers because they can be expressed as a fraction with 1 as the denominator. For example:
- 5 can be written as \(\frac{5}{1}\)
- -3 can be written as \(\frac{-3}{1}\)
- Finite Decimals: Any finite decimal can be converted into a fraction. For example:
- 0.5 can be written as \(\frac{1}{2}\)
- 2.75 can be written as \(\frac{11}{4}\)
- Repeating Decimals: Decimals that have a repeating pattern can be expressed as fractions. For example:
- 0.333... (repeating 3) can be written as \(\frac{1}{3}\)
- 0.142857... (repeating 142857) can be written as \(\frac{1}{7}\)
- Fractions: Any number in the form of a fraction where both the numerator and the denominator are integers, and the denominator is not zero. For example:
- \(\frac{7}{2}\)
- \(\frac{-9}{4}\)
- Mixed Numbers: Mixed numbers are also rational because they can be converted to improper fractions. For example:
- 3 1/2 can be written as \(\frac{7}{2}\)
- -1 3/4 can be written as \(\frac{-7}{4}\)
Here is a table summarizing some examples of rational numbers:
| Number | Fraction Form | Rational? |
|---|---|---|
| 5 | \(\frac{5}{1}\) | Yes |
| 0.75 | \(\frac{3}{4}\) | Yes |
| 0.333... | \(\frac{1}{3}\) | Yes |
| 7/8 | \(\frac{7}{8}\) | Yes |
| 2 1/2 | \(\frac{5}{2}\) | Yes |
Rational numbers play a crucial role in mathematics, as they help in understanding various concepts such as ratios, proportions, and real-world problems involving measurements and divisions.

Definition of Irrational Numbers
An irrational number is a real number that cannot be expressed as a simple fraction (i.e., it is not a rational number). Specifically, an irrational number has an infinite and non-repeating decimal expansion. These numbers cannot be represented as the quotient of two integers and include examples such as the square root of non-perfect squares (like √2 and √3), transcendental numbers (like π and e), and others.
Properties of Square Roots
- The square root of a number, denoted as √x, is a value that, when multiplied by itself, gives x.
- If x is a positive number, then √x is also positive.
- The square root of 1, denoted as √1, equals 1, which is a rational number.
- For non-perfect squares, the square root is typically an irrational number with an infinite decimal expansion.
- Square roots obey specific arithmetic properties, such as √(x * y) = √x * √y and √(x / y) = √x / √y, for non-negative numbers x and y.
- Complex numbers can also have square roots, extending the concept beyond real numbers.
Calculation of Square Root of 1
- The square root of 1, denoted as √1, is calculated as follows:
- Since 1 is a perfect square, √1 equals 1.
- This can be represented mathematically as √1 = 1.
- Therefore, the square root of 1 is a rational number because it can be expressed as a simple fraction, specifically 1.
Mathematical Representation of Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. It is represented mathematically using the radical symbol (√). For example, the square root of 9 is written as √9, which equals 3, since 3 * 3 = 9.
Mathematically, we can represent the square root operation as:
\[ \sqrt{n} = x \]
where \( n \) is the number and \( x \) is the square root of \( n \). This implies:
\[ x^2 = n \]
For example, to find the square root of 1, we set:
\[ \sqrt{1} = x \]
which means:
\[ x^2 = 1 \]
Since 1 is a perfect square, its square root is a whole number:
\[ \sqrt{1} = 1 \]
This demonstrates that the square root of 1 is 1, making it a rational number because it can be expressed as a fraction:
\[ 1 = \frac{1}{1} \]
In general, the square root of any non-negative integer that is a perfect square is a rational number. For non-perfect squares, the square roots are typically irrational.
For instance:
- √4 = 2 (rational)
- √9 = 3 (rational)
- √2 ≈ 1.414 (irrational)
This highlights the difference between rational and irrational numbers in the context of square roots.
Is 1 a Rational Number?
To determine whether 1 is a rational number, we first need to understand the definition of rational numbers. A rational number is any number that can be expressed as the quotient or fraction p/q of two integers, where p (the numerator) and q (the denominator) are integers, and q is not equal to zero. In mathematical terms, a number r is rational if:
\( r = \frac{p}{q} \), where \( p \in \mathbb{Z} \) and \( q \in \mathbb{Z} \setminus \{0\} \).
Given this definition, we can check if 1 fits the criteria for being a rational number:
- Express 1 as a fraction: \( 1 = \frac{1}{1} \).
- In this fraction, both the numerator (1) and the denominator (1) are integers.
- The denominator is not zero.
Since 1 can be written as \( \frac{1}{1} \), which satisfies the condition of being a fraction of two integers with a non-zero denominator, 1 is indeed a rational number.
Additionally, 1 can be expressed in many other forms as a fraction, such as \( \frac{2}{2} \), \( \frac{3}{3} \), or generally \( \frac{n}{n} \), where \( n \) is any non-zero integer. This further confirms that 1 is a rational number.
Therefore, we conclude that 1 meets all the criteria to be classified as a rational number.
Is -1 a Rational Number?
To determine whether -1 is a rational number, we first need to understand the definition of rational numbers. A rational number is any number that can be expressed as the quotient or fraction p/q of two integers, where p and q are integers, and q is not equal to zero.
Let's analyze -1 based on this definition:
Representation as a Fraction: The number -1 can be written as a fraction in several ways, such as -1/1, -2/2, -3/3, etc. In each case, -1 is represented as the quotient of two integers.
Integers Involved: In the fractions mentioned above, both the numerator and the denominator are integers. For example, in the fraction -1/1, -1 is an integer and 1 is also an integer.
Non-zero Denominator: The denominator in these fractions is not zero. This is a crucial requirement for a number to be considered rational, and -1 satisfies this condition in all its fractional representations.
Therefore, based on the definition of rational numbers, -1 is indeed a rational number because it can be expressed as a fraction where both the numerator and the denominator are integers, and the denominator is not zero.
Rationality of Square Root of 1
The square root of a number is a value that, when multiplied by itself, gives the original number. In the case of the square root of 1, we need to find a number which, when squared, results in 1.
The square root of 1 is 1, because:
\[
1 \times 1 = 1
\]
To determine if the square root of 1 is a rational number, we first need to understand the definition of rational numbers. A rational number is any number that can be expressed as the quotient or fraction \(\frac{p}{q}\) of two integers \(p\) and \(q\), where \(q\) is not zero.
The number 1 can be written as \(\frac{1}{1}\), which is a ratio of two integers. Therefore, 1 is a rational number. Since the square root of 1 is 1, we can conclude that the square root of 1 is also a rational number.
Here is the step-by-step reasoning:
- Identify the square root of 1: \( \sqrt{1} = 1 \).
- Express 1 as a fraction: \(\frac{1}{1}\).
- Verify that both numerator and denominator are integers.
- Confirm that the denominator is not zero.
- Since \(\frac{1}{1}\) is a valid fraction of two integers, 1 is a rational number.
- Thus, the square root of 1 is rational.
To further illustrate, consider the following table of square roots and their rationality:
| Number | Square Root | Rational or Irrational |
|---|---|---|
| 1 | 1 | Rational |
| 4 | 2 | Rational |
| 9 | 3 | Rational |
| 2 | \(\sqrt{2}\) | Irrational |
| 3 | \(\sqrt{3}\) | Irrational |
As demonstrated, the square root of 1 is indeed a rational number.
Examples of Rational and Irrational Square Roots
Square roots can be classified as rational or irrational numbers based on their properties. Below are some examples to illustrate these classifications:
Rational Square Roots
A rational number is any number that can be expressed as the quotient or fraction \( \frac{p}{q} \) of two integers, where \( p \) and \( q \) are integers and \( q \neq 0 \).
- \(\sqrt{1} = 1\) (since \(1 = \frac{1}{1}\))
- \(\sqrt{4} = 2\) (since \(2 = \frac{2}{1}\))
- \(\sqrt{9} = 3\) (since \(3 = \frac{3}{1}\))
- \(\sqrt{16} = 4\) (since \(4 = \frac{4}{1}\))
Irrational Square Roots
An irrational number is a number that cannot be expressed as a simple fraction; its decimal form is non-terminating and non-repeating.
- \(\sqrt{2} \approx 1.414213...\)
- \(\sqrt{3} \approx 1.732050...\)
- \(\sqrt{5} \approx 2.236067...\)
- \(\sqrt{7} \approx 2.645751...\)
Comparison Table
| Number | Square Root | Rational/Irrational |
|---|---|---|
| 1 | \(\sqrt{1} = 1\) | Rational |
| 2 | \(\sqrt{2} \approx 1.414213...\) | Irrational |
| 4 | \(\sqrt{4} = 2\) | Rational |
| 3 | \(\sqrt{3} \approx 1.732050...\) | Irrational |
| 9 | \(\sqrt{9} = 3\) | Rational |
| 5 | \(\sqrt{5} \approx 2.236067...\) | Irrational |
| 16 | \(\sqrt{16} = 4\) | Rational |
| 7 | \(\sqrt{7} \approx 2.645751...\) | Irrational |
In summary, the rationality of a square root depends on whether the original number is a perfect square. If it is, its square root is rational; otherwise, it is irrational.
Conclusion on Rationality of Square Root of 1
The square root of 1 is a rational number. By definition, a rational number is any number that can be expressed as the quotient of two integers where the denominator is not zero. In mathematical terms, this can be written as:
\[ \text{Rational Number} = \frac{a}{b} \] where \( a \) and \( b \) are integers and \( b \neq 0 \).
For the square root of 1, we have:
\[ \sqrt{1} = 1 \]
Since 1 can be expressed as \(\frac{1}{1}\), it clearly fits the definition of a rational number.
In summary, the calculation of the square root of 1 demonstrates that it is rational because:
- The square root of 1 is 1.
- 1 is a whole number and can be written as a fraction with 1 as the numerator and 1 as the denominator.
This fundamental property confirms that the square root of 1 is indeed rational. Hence, \(\sqrt{1} = 1\) is a straightforward and classic example of a rational number.
Hướng dẫn cách đơn giản hóa căn bậc hai của một số hữu tỉ để thu hút người xem. Video phù hợp với bài viết 'căn bậc hai của 1 có phải là số hữu tỉ không?'
Đơn Giản Hóa Căn Bậc Hai Của Một Số Hữu Tỉ
READ MORE:
Video này giải thích khái niệm về gốc bình phương và làm thế nào để tính toán chúng. Hãy cùng thầy J khám phá và học toán dễ dàng!
Gốc Bình Phương Là Gì? | Toán Học Với Thầy J