Topic what is six squared: Discover the concept of six squared and how to calculate it effortlessly. This article breaks down the meaning of squaring a number, provides a simple calculation of 6 squared, and explains its importance in mathematics. Dive in to enhance your understanding and master this fundamental mathematical operation.
Table of Content
- What is Six Squared?
- Introduction to Six Squared
- Definition of Squaring a Number
- Mathematical Explanation and Steps
- Visual Representation of Six Squared
- Applications of Squaring Numbers
- Importance of Understanding Exponents
- Common Mistakes and Misunderstandings
- Practice Problems and Solutions
- Conclusion and Summary
- YOUTUBE:
What is Six Squared?
In mathematics, "six squared" means raising the number six to the power of two. This is denoted as \( 6^2 \). Squaring a number means multiplying the number by itself.
Calculation of Six Squared
To calculate six squared, you multiply 6 by itself:
\[ 6^2 = 6 \times 6 = 36 \]
Explanation
Here is a step-by-step breakdown of the calculation:
- Start with the number 6.
- Multiply 6 by itself: \( 6 \times 6 \).
- The result of the multiplication is 36.
Visual Representation
You can visualize six squared as a 6x6 grid:
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 2 | 3 | 4 | 5 | 6 |
Conclusion
Therefore, six squared is \( 6^2 = 36 \). This simple operation is fundamental in mathematics and appears frequently in various mathematical contexts.

READ MORE:
Introduction to Six Squared
In mathematics, "six squared" refers to raising the number six to the power of two. This operation is represented as \( 6^2 \). Squaring a number means multiplying the number by itself. Here is a detailed explanation:
- Start with the base number, which is 6 in this case.
- Multiply the base number by itself: \( 6 \times 6 \).
- The result of this multiplication is 36, so \( 6^2 = 36 \).
To visualize six squared, imagine a 6 by 6 grid, where each cell represents one unit:
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 2 | 3 | 4 | 5 | 6 |
Each row and column of the grid has 6 cells, and the total number of cells is \( 6 \times 6 = 36 \). This simple yet powerful operation is fundamental in various branches of mathematics, from algebra to geometry. Understanding how to square numbers is crucial for solving more complex mathematical problems.
Definition of Squaring a Number
Squaring a number is a fundamental mathematical operation where a number is multiplied by itself. This is also known as raising a number to the power of two. The notation for squaring a number uses an exponent of 2. Here is a step-by-step explanation:
- Identify the base number that you want to square. Let's denote this number as \( x \).
- Multiply the base number by itself: \( x \times x \).
- The result of this multiplication is the square of the number, represented as \( x^2 \).
For example, to square the number 6:
- Start with the base number: 6.
- Multiply it by itself: \( 6 \times 6 \).
- The result is: \( 6^2 = 36 \).
This operation can be visualized using a geometric representation. If you consider a square with side length \( x \), the area of the square is \( x^2 \). For instance, if the side length is 6, the area of the square is \( 6^2 = 36 \) square units.
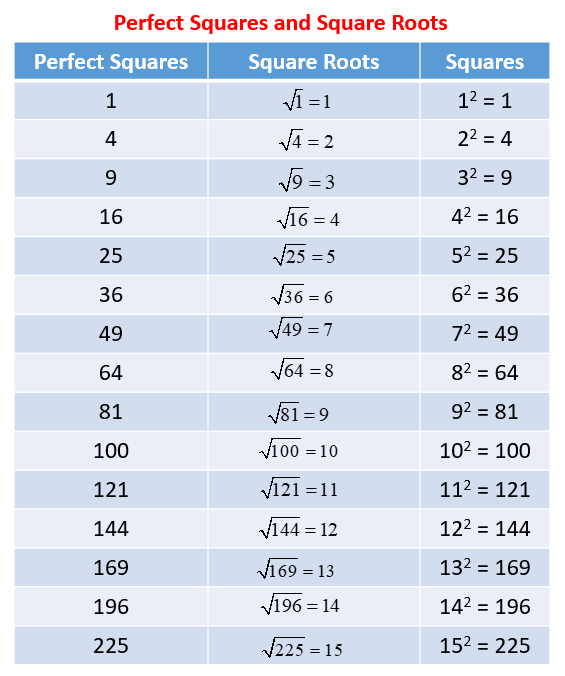
Here is a table summarizing the squares of some common numbers:
| Number | Square |
|---|---|
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
| 5 | 25 |
| 6 | 36 |
Understanding the concept of squaring a number is crucial for solving a wide range of mathematical problems, from basic arithmetic to advanced algebra and geometry.
Mathematical Explanation and Steps
Squaring a number involves raising that number to the power of two. Here, we will explain and demonstrate the steps involved in squaring the number 6. This process is simple and foundational in mathematics.
- Identify the base number: The base number we are working with is 6.
- Understand the exponent: Squaring means raising the number to the power of 2, which is written as \( 6^2 \).
- Perform the multiplication: Multiply the base number by itself.
- \( 6 \times 6 \)
- Calculate the result: The result of multiplying 6 by 6 is 36.
- \( 6 \times 6 = 36 \)
To visualize this process, consider the following steps:
- Step 1: Start with the base number 6.
- Step 2: Multiply 6 by 6.
- Step 3: Obtain the result, which is 36.
This can also be demonstrated in a more detailed manner:
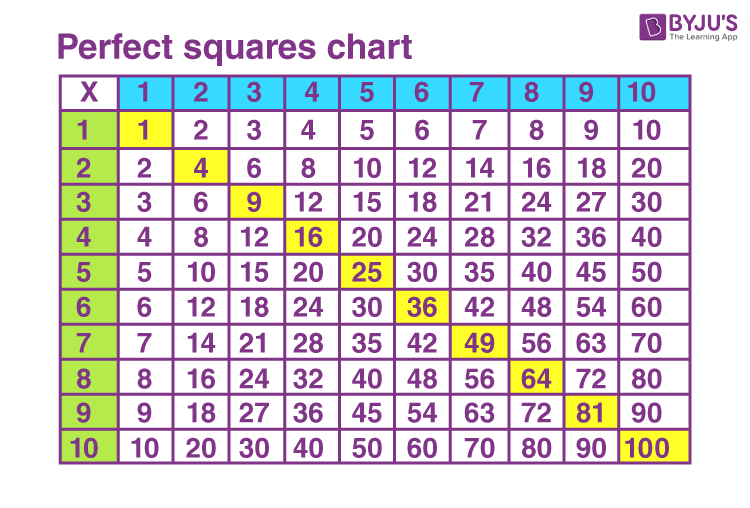
| Operation | Calculation | Result |
|---|---|---|
| 6 multiplied by 1 | 6 × 1 | 6 |
| 6 multiplied by 2 | 6 × 2 | 12 |
| 6 multiplied by 3 | 6 × 3 | 18 |
| 6 multiplied by 4 | 6 × 4 | 24 |
| 6 multiplied by 5 | 6 × 5 | 30 |
| 6 multiplied by 6 | 6 × 6 | 36 |
Thus, the mathematical explanation of squaring the number 6 shows that \( 6^2 = 36 \). This operation is fundamental and widely used in various fields of mathematics, making it essential to understand and master.
Visual Representation of Six Squared
Visualizing six squared can help in understanding the concept more clearly. Squaring the number 6 means creating a square with side lengths of 6 units each. The area of this square represents \( 6^2 \), which is 36 square units. Let's break this down step by step:
- Start with a square shape.
- Each side of the square measures 6 units.
- To find the area of the square, multiply the length of one side by itself:
- \( 6 \times 6 \)
- The result is the area of the square, which is 36 square units:
- \( 6^2 = 36 \)
To visualize this concept, consider a grid where each cell represents one unit. A 6 by 6 grid will contain 36 cells in total, demonstrating \( 6^2 = 36 \).
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 2 | 3 | 4 | 5 | 6 |
In this grid:
- Each row has 6 cells.
- Each column has 6 cells.
- Total number of cells is \( 6 \times 6 = 36 \).
This visual representation helps to solidify the concept that squaring a number involves creating a square with equal side lengths, and the area of that square represents the squared value.

Applications of Squaring Numbers
Squaring numbers is a fundamental mathematical operation with a wide range of applications across various fields. Understanding how to square numbers and apply this knowledge can be very useful. Here are some of the key applications:
1. Geometry and Area Calculation
Squaring is essential in geometry, particularly for calculating the area of squares and other geometric shapes. For example, if you have a square with side length \( x \), the area is given by \( x^2 \). This principle extends to calculating areas in more complex geometric figures as well.
2. Physics and Engineering
In physics and engineering, squaring numbers appears in various formulas and equations. For example:
- Calculating kinetic energy: \( KE = \frac{1}{2}mv^2 \) (where \( m \) is mass and \( v \) is velocity).
- Determining gravitational potential energy: \( U = mgh \) (where \( g \) is acceleration due to gravity and \( h \) is height).
3. Statistics
In statistics, squaring numbers is used to calculate variance and standard deviation, which are measures of data dispersion. For example:
- Variance: \( \sigma^2 = \frac{1}{N}\sum_{i=1}^{N}(x_i - \mu)^2 \)
- Standard Deviation: \( \sigma = \sqrt{\frac{1}{N}\sum_{i=1}^{N}(x_i - \mu)^2} \)
4. Algebra
Squaring numbers is fundamental in solving quadratic equations of the form \( ax^2 + bx + c = 0 \). The quadratic formula \( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \) involves squaring the coefficient \( b \).
5. Computer Science
In computer science, squaring numbers is used in algorithms and data structures, such as calculating hash functions, performing binary exponentiation, and analyzing the time complexity of algorithms (e.g., \( O(n^2) \) complexity).
6. Everyday Life
Squaring numbers also finds applications in daily life, such as:
- Estimating areas for construction projects.
- Understanding rates of growth or decay in financial contexts.
- Calculating power consumption (e.g., the power dissipated in a resistor \( P = I^2R \)).
Overall, the concept of squaring numbers is integral to many aspects of both theoretical and practical mathematics. Mastery of this operation opens doors to solving complex problems and understanding deeper mathematical relationships.
Importance of Understanding Exponents
Understanding exponents is a crucial aspect of mathematics that extends far beyond basic arithmetic. Exponents, including the concept of squaring, provide a foundation for more complex mathematical concepts and real-world applications. Here are several reasons why understanding exponents is important:
1. Simplification of Large Numbers
Exponents allow for the simplification and compact representation of very large or very small numbers. For instance, \( 10^6 \) is a much simpler way to write 1,000,000.
2. Algebra and Equations
Exponents are fundamental in algebra, particularly when solving equations involving powers and roots. For example:
- Quadratic equations: \( ax^2 + bx + c = 0 \)
- Exponential growth and decay: \( y = a \cdot e^{kt} \)
3. Scientific Notation
Scientific notation relies on exponents to express large and small numbers efficiently, which is essential in fields such as physics, chemistry, and engineering. For example, the speed of light is approximately \( 3 \times 10^8 \) meters per second.
4. Geometry and Area Calculation
In geometry, understanding exponents is vital for calculating areas and volumes. The area of a square is given by \( s^2 \), where \( s \) is the length of a side. Similarly, the volume of a cube is \( s^3 \).
5. Understanding Growth Patterns
Exponential growth and decay are common in various natural and financial processes. Examples include population growth, radioactive decay, and compound interest calculations:
- Compound interest formula: \( A = P(1 + \frac{r}{n})^{nt} \)
6. Computer Science and Algorithms
Exponents are used in computer science for algorithm analysis, particularly in calculating the time complexity of algorithms. Understanding exponential growth helps in evaluating the efficiency of algorithms:
- Time complexity: \( O(2^n) \)
7. Physics and Engineering
In physics and engineering, exponents are used in various formulas and laws. For instance, Newton's law of universal gravitation involves squaring the distance between two masses:
- Gravitational force: \( F = G \frac{m_1 m_2}{r^2} \)
8. Financial Mathematics
Exponents are crucial in financial mathematics, particularly in calculating interest rates, annuities, and investment growth over time:
- Future value of an investment: \( FV = PV(1 + r)^n \)
Understanding exponents is not only fundamental to advancing in mathematics but also essential for practical applications in science, engineering, finance, and technology. Mastery of exponents enables individuals to tackle complex problems and understand the underlying principles governing various natural and man-made phenomena.
Common Mistakes and Misunderstandings
When learning about squaring numbers, especially simple cases like six squared, there are several common mistakes and misunderstandings that students often encounter. Understanding these pitfalls can help learners avoid them and grasp the concept more effectively.
- Misinterpreting the Squaring Operation:
One of the most common mistakes is misinterpreting what it means to square a number. Squaring a number means multiplying the number by itself, not by two. For example:
\[
6^2 = 6 \times 6 = 36
\]Some students might mistakenly think that \(6^2\) means \(6 \times 2\), which equals 12. This is incorrect.
- Confusing Exponents with Multiplication:
Students often confuse squaring a number with simple multiplication. It's crucial to remember that squaring involves an exponent. For example:
\[
6^2 \neq 6 \times 2
\]The correct interpretation is:
\[
6^2 = 6 \times 6
\]which results in 36.
- Neglecting the Order of Operations:
Another common mistake is neglecting the order of operations. When an equation involves exponents, those operations should be performed before multiplication or addition. For example:
\[
2 + 6^2 \neq (2 + 6)^2
\]The correct calculation is:
\[
2 + 6^2 = 2 + 36 = 38
\]While \((2 + 6)^2\) equals 64.
- Incorrectly Squaring Negative Numbers:
When squaring negative numbers, students often make mistakes. It's important to square the negative number correctly. For example:
\[
(-6)^2 = (-6) \times (-6) = 36
\]Note that squaring a negative number results in a positive value.
- Misplacing Parentheses:
Misplacing parentheses can lead to incorrect results. The position of parentheses affects the outcome of the operation. For example:
\[
-6^2 \neq (-6)^2
\]\[
-6^2 = - (6 \times 6) = -36
\]While
\[
(-6)^2 = (-6) \times (-6) = 36
\]
By understanding and avoiding these common mistakes, students can more accurately perform squaring operations and better grasp the concept of exponents.
Practice Problems and Solutions
Practicing squaring numbers helps reinforce the concept and ensures a solid understanding. Below are some practice problems along with detailed solutions to guide you through the process.
- Problem 1:
What is the square of 7?
Solution:
To find the square of 7, multiply 7 by itself:
\[
7^2 = 7 \times 7 = 49
\] - Problem 2:
Calculate \(4^2\).
Solution:
To find \(4^2\), multiply 4 by itself:
\[
4^2 = 4 \times 4 = 16
\] - Problem 3:
Find the value of \(10^2\).
Solution:
To determine \(10^2\), multiply 10 by itself:
\[
10^2 = 10 \times 10 = 100
\] - Problem 4:
What is the square of 12?
Solution:
To find the square of 12, multiply 12 by itself:
\[
12^2 = 12 \times 12 = 144
\] - Problem 5:
Solve for \(5^2\).
Solution:
To find \(5^2\), multiply 5 by itself:
\[
5^2 = 5 \times 5 = 25
\]
Let's also practice squaring negative numbers to understand how the sign affects the result.
- Problem 6:
What is the square of \(-3\)?
Solution:
To find the square of \(-3\), multiply \(-3\) by itself:
\[
(-3)^2 = (-3) \times (-3) = 9
\] - Problem 7:
Calculate \((-8)^2\).
Solution:
To determine \((-8)^2\), multiply \(-8\) by itself:
\[
(-8)^2 = (-8) \times (-8) = 64
\]
Finally, here are a few mixed practice problems to test your understanding:
- Problem 8:
Find the value of \(9^2 + 6^2\).
Solution:
First, calculate each square:
\[
9^2 = 9 \times 9 = 81
\]\[
6^2 = 6 \times 6 = 36
\]Then, add the results:
\[
81 + 36 = 117
\] - Problem 9:
What is the result of \(7^2 - 4^2\)?
Solution:
First, calculate each square:
\[
7^2 = 7 \times 7 = 49
\]\[
4^2 = 4 \times 4 = 16
\]Then, subtract the results:
\[
49 - 16 = 33
\] - Problem 10:
Solve for \((2 + 3)^2\).
Solution:
First, calculate the sum inside the parentheses:
\[
2 + 3 = 5
\]Then, square the result:
\[
5^2 = 5 \times 5 = 25
\]

Conclusion and Summary
Understanding the concept of squaring numbers, such as six squared, is fundamental in mathematics. This knowledge is not only essential for more advanced mathematical concepts but also has practical applications in various fields.
- Key Takeaways:
- Squaring a number means multiplying the number by itself. For example:
- Squaring is an important operation that helps in understanding exponents and other mathematical principles.
\[
6^2 = 6 \times 6 = 36
\] - Common Mistakes to Avoid:
- Do not confuse squaring with doubling a number. Squaring involves multiplication, not addition.
- Pay attention to the order of operations to avoid errors in calculations involving exponents.
- Remember to square negative numbers correctly, which results in a positive value.
- Practice and Application:
- Regular practice with problems involving squaring numbers can reinforce understanding and improve accuracy.
- Applications of squaring numbers extend to areas such as geometry, physics, and computer science.
- Final Thoughts:
Mastering the concept of squaring numbers lays a solid foundation for further mathematical learning. It enhances problem-solving skills and helps in comprehending more complex mathematical operations. By understanding the process, avoiding common mistakes, and practicing regularly, students can gain confidence and proficiency in working with exponents.
In summary, six squared is a straightforward yet powerful example of how fundamental mathematical concepts are built. Emphasizing the importance of clear understanding and correct application ensures a strong mathematical foundation for all learners.
6 bình phương là gì?
READ MORE:
Có sự khác biệt không? -6 bình phương vs. (-6) bình phương vs. 6 bình phương