Topic what is b squared: What is b squared? Discover the fundamental concept of squaring a number, denoted as \( b^2 \). Learn how this mathematical operation is defined, its properties, and its real-world applications in fields like geometry, physics, and statistics. Dive into examples and advanced concepts to deepen your understanding of \( b^2 \).
Table of Content
- Understanding \( b^2 \)
- Introduction to \( b^2 \) (b Squared)
- Mathematical Definition and Basic Concepts
- Properties of Squared Numbers
- Geometric Interpretations and Applications
- Squared Numbers in Algebra
- Exponential Rules Involving \( b^2 \)
- Examples of Squaring Different Types of Numbers
- Real-world Applications of Squared Numbers
- Squared Numbers in Geometry
- Physics Applications of Squared Numbers
- Statistics and Squared Numbers
- Common Mistakes and Misconceptions
- Advanced Concepts Related to Squaring Numbers
- Conclusion and Further Reading
- YOUTUBE:
Understanding \( b^2 \)
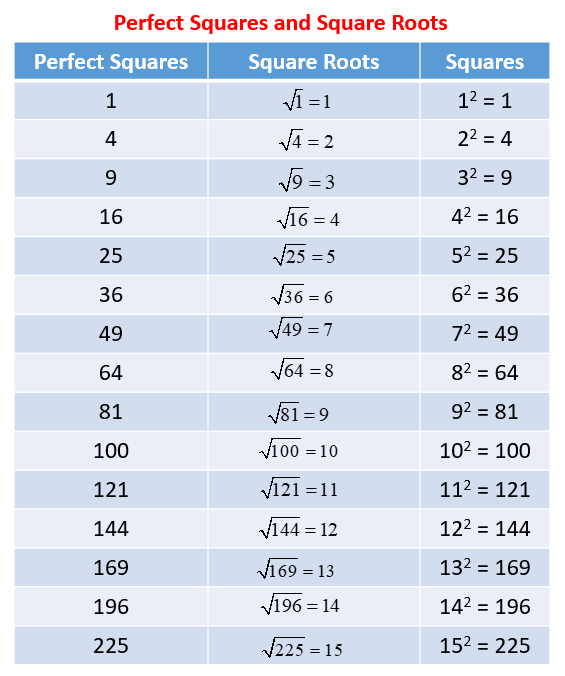
The term \( b^2 \) (read as "b squared") refers to the mathematical operation of raising the variable \( b \) to the power of 2. This is a fundamental concept in algebra and can be applied in various mathematical contexts. Below, we provide a detailed explanation and examples to help you understand \( b^2 \).
Definition
In mathematics, squaring a number means multiplying the number by itself. Therefore:
\[ b^2 = b \times b \]
Properties of \( b^2 \)
- Non-Negativity: The square of any real number \( b \) is always non-negative. That is, \( b^2 \geq 0 \).
- Symmetry: The square of a number and its negative are equal. For instance, \( b^2 = (-b)^2 \).
- Exponential Rules: Squaring is a specific case of the general exponentiation rule \( b^n \). For example, \( b^2 \) follows the same properties as other exponents:
\[ (b^m)^n = b^{mn} \]
Thus, \( (b^2)^3 = b^{2 \times 3} = b^6 \).
Examples
To illustrate \( b^2 \), let's look at some examples:
- When \( b = 3 \): \( 3^2 = 3 \times 3 = 9 \)
- When \( b = -4 \): \( (-4)^2 = (-4) \times (-4) = 16 \)
- When \( b = 0.5 \): \( (0.5)^2 = 0.5 \times 0.5 = 0.25 \)
Applications
Squaring numbers is useful in various fields, such as:
- Geometry: Calculating the area of a square, where the area is \( b^2 \) and \( b \) is the length of a side.
- Physics: Formulas involving kinetic energy, where \( KE = \frac{1}{2}mv^2 \) and \( v \) is velocity.
- Statistics: Variance calculation, where differences are squared to avoid negative values.
Conclusion
Understanding \( b^2 \) is essential for solving various mathematical problems. It represents the product of a number with itself and has numerous applications in different fields. Mastering this concept is foundational for further studies in mathematics and science.

READ MORE:
Introduction to \( b^2 \) (b Squared)
The notation \( b^2 \) represents the square of a number \( b \). In mathematical terms, squaring a number means multiplying the number by itself. Hence, \( b^2 = b \times b \).
Squaring is a fundamental operation in mathematics, with applications spanning across various fields such as algebra, geometry, physics, and statistics. Understanding \( b^2 \) helps in grasping more complex mathematical concepts and solving real-world problems.
Here are some key points to understand about \( b^2 \):
- Basic Definition: If \( b \) is a real number, then \( b^2 \) is the product of \( b \) and \( b \).
- Positive and Negative Numbers: Both positive and negative numbers can be squared. The square of a positive number is positive, and the square of a negative number is also positive. For example, \( (3)^2 = 9 \) and \( (-3)^2 = 9 \).
- Zero: The square of zero is zero, i.e., \( 0^2 = 0 \).
- Properties: Squaring a number always results in a non-negative number.
To visualize this concept, consider the following table:
| Number (b) | Square (b^2) |
|---|---|
| 2 | 4 |
| -2 | 4 |
| 0 | 0 |
| 1.5 | 2.25 |
Understanding \( b^2 \) lays the foundation for exploring more advanced topics in mathematics. It is a critical step in algebraic manipulations, solving quadratic equations, and analyzing geometric shapes. Moreover, squared numbers appear frequently in formulas across different scientific disciplines, making it an essential concept to master.
Mathematical Definition and Basic Concepts
In mathematics, squaring a number means multiplying the number by itself. When we write \( b^2 \), we are expressing the operation of squaring the variable \( b \). This can be formulated as:
\[ b^2 = b \times b \]
Here are some basic concepts related to squaring numbers:
- Positive and Negative Numbers: When you square any real number, whether positive or negative, the result is always non-negative. For example:
- \( 3^2 = 3 \times 3 = 9 \)
- \( (-3)^2 = (-3) \times (-3) = 9 \)
- Zero: The square of zero is zero:
- \( 0^2 = 0 \times 0 = 0 \)
- Exponentiation: Squaring is a specific instance of exponentiation where the exponent is 2. In general, exponentiation involves raising a base \( b \) to an exponent \( n \), written as \( b^n \):
- \( b^2 \) means \( b \) raised to the power of 2.
- Properties: Squaring has several important properties:
- Distributive Property: \((a + b)^2 = a^2 + 2ab + b^2\)
- Associative Property: \( (ab)^2 = a^2 \times b^2 \)
- Identity Element: \( 1^2 = 1 \)
Let's see an example of applying the distributive property:
\[ (a + b)^2 = a^2 + 2ab + b^2 \]
For instance, if \( a = 2 \) and \( b = 3 \), then:
\[ (2 + 3)^2 = 2^2 + 2(2)(3) + 3^2 = 4 + 12 + 9 = 25 \]
Understanding these basic concepts of squaring numbers is fundamental in algebra and helps in various mathematical applications.
Properties of Squared Numbers
Squared numbers, or numbers raised to the power of two, have several important properties. Understanding these properties helps in various mathematical and real-world applications.
- Non-Negativity: The square of any real number is always non-negative. This means \( b^2 \geq 0 \) for any real number \( b \). For example:
- \((3)^2 = 9\)
- \((-3)^2 = 9\)
- \((0)^2 = 0\)
- Even Powers of Even Numbers: When an even number is squared, the result is also an even number. For example:
- \((2)^2 = 4\)
- \((4)^2 = 16\)
- Odd Powers of Odd Numbers: When an odd number is squared, the result is also an odd number. For example:
- \((3)^2 = 9\)
- \((5)^2 = 25\)
- Distributive Property: Squaring a sum is not the same as summing the squares. For example:
\((a + b)^2 \neq a^2 + b^2\). Instead, \((a + b)^2 = a^2 + 2ab + b^2\).
- Product Property: The square of a product is equal to the product of the squares. For example:
\((ab)^2 = a^2 \cdot b^2\)
- Graphical Representation: When plotted on a graph, the function \( y = b^2 \) forms a parabola that opens upwards.
These properties are foundational in algebra, geometry, and various fields of science, providing critical insights into how squared numbers behave under different operations.
Geometric Interpretations and Applications
Understanding the geometric interpretations of squared numbers opens up a range of practical applications, especially in fields such as geometry and physics. Squaring a number geometrically can be visualized as creating a square where the side length of the square is the given number, \( b \).
Let's explore some key geometric interpretations and their applications:
- Area of a Square: The most straightforward geometric interpretation of \( b^2 \) is the area of a square with side length \( b \). If a square has each side of length \( b \), then its area is given by \( b^2 \). For example, if \( b = 4 \), the area of the square is \( 4^2 = 16 \) square units.
- Pythagorean Theorem: In a right-angled triangle, the relationship between the lengths of the sides is expressed by the Pythagorean theorem, which states \( a^2 + b^2 = c^2 \), where \( c \) is the hypotenuse. This theorem is crucial for calculating distances in various applications, such as construction and navigation.
- Geometric Transformations: Squaring is often involved in transformations such as scaling. For instance, if a geometric shape is scaled by a factor of \( b \), the area scales by \( b^2 \). This principle is used in computer graphics and design to resize shapes while maintaining proportional areas.
- Volume Calculations: When extending the concept to three dimensions, squaring is used in volume calculations. For instance, the volume of a cube with side length \( b \) is \( b^3 \), where the base area is \( b^2 \) and is multiplied by the height \( b \).
These geometric interpretations are not just theoretical; they have practical implications in various fields:
- Architecture: Calculating areas and volumes using squared numbers helps in designing buildings and structures, ensuring they are both aesthetically pleasing and structurally sound.
- Physics: In physics, squared quantities frequently appear in formulas, such as calculating the force of gravity (proportional to the square of the distance) or in the equations of motion.
- Computer Graphics: Understanding geometric transformations involving squared numbers aids in developing algorithms for rendering images and animations with accurate scaling and rotation.
Overall, the geometric interpretations and applications of \( b^2 \) (b squared) demonstrate its fundamental role in both mathematics and real-world problem-solving.
Squared Numbers in Algebra
In algebra, squaring a number is a fundamental operation that has significant implications and applications. Squaring a number \( b \) means multiplying it by itself, which is expressed mathematically as \( b^2 \). This operation transforms both positive and negative numbers into positive results due to the property that a negative times a negative yields a positive.
Some key algebraic concepts related to squared numbers include:
- Quadratic Equations: These are polynomial equations of the form \( ax^2 + bx + c = 0 \). The solutions to these equations can be found using methods such as factoring, completing the square, or the quadratic formula, which heavily relies on the squared term \( b^2 \).
- Graph of the Square Function: The function \( y = b^2 \) produces a parabola when graphed. This shape is symmetric about the y-axis and has its vertex at the origin (0,0), illustrating how the value of \( b^2 \) grows rapidly as \( b \) increases or decreases from zero.
- Monotonic Properties: The squaring function is monotonically increasing for non-negative numbers (as \( b \) increases, \( b^2 \) also increases) and monotonically decreasing for negative numbers (as \( b \) becomes more negative, \( b^2 \) increases).
- Zero and Positive Roots: Every positive number has two square roots: one positive and one negative. Zero has only one square root, which is itself.
Additionally, in algebra, squaring plays a critical role in solving quadratic equations. The standard form of a quadratic equation is:
\[
ax^2 + bx + c = 0
\]
where \( a \), \( b \), and \( c \) are constants. The quadratic formula, derived from completing the square, is used to find the solutions (roots) of the equation:
\[
x = \frac{{-b \pm \sqrt{{b^2 - 4ac}}}}{2a}
\]
This formula shows how the discriminant \( b^2 - 4ac \) determines the nature of the roots (real and distinct, real and repeated, or complex). The term \( b^2 \) within the discriminant highlights the importance of the squaring operation in algebraic solutions.
In summary, squared numbers are integral to algebraic structures and equations, providing essential insights and tools for solving polynomial equations and understanding the behavior of functions.
Exponential Rules Involving \( b^2 \)
The rules of exponents are fundamental for understanding how to manipulate expressions involving powers, including \( b^2 \). Here are some of the key exponential rules involving squared terms:
- Product of Powers: When multiplying two expressions with the same base, you add the exponents. \[ b^m \cdot b^n = b^{m+n} \] For example, \( b^2 \cdot b^3 = b^{2+3} = b^5 \).
- Power of a Power: When raising an exponent to another power, you multiply the exponents. \[ (b^m)^n = b^{m \cdot n} \] For example, \( (b^2)^3 = b^{2 \cdot 3} = b^6 \).
- Power of a Product: When raising a product to a power, you apply the exponent to each factor in the product. \[ (ab)^n = a^n \cdot b^n \] For example, \( (3b)^2 = 3^2 \cdot b^2 = 9b^2 \).
- Power of a Quotient: When raising a quotient to a power, you apply the exponent to both the numerator and the denominator. \[ \left(\frac{a}{b}\right)^n = \frac{a^n}{b^n} \] For example, \( \left(\frac{3}{b}\right)^2 = \frac{3^2}{b^2} = \frac{9}{b^2} \).
- Zero Exponent: Any non-zero base raised to the power of zero is equal to one. \[ b^0 = 1 \quad \text{for} \quad b \ne 0 \]
- Negative Exponent: A negative exponent indicates the reciprocal of the base raised to the positive exponent. \[ b^{-n} = \frac{1}{b^n} \] For example, \( b^{-2} = \frac{1}{b^2} \).
Understanding these rules allows for the simplification and manipulation of algebraic expressions involving exponents, which is essential for solving equations and performing various algebraic operations.
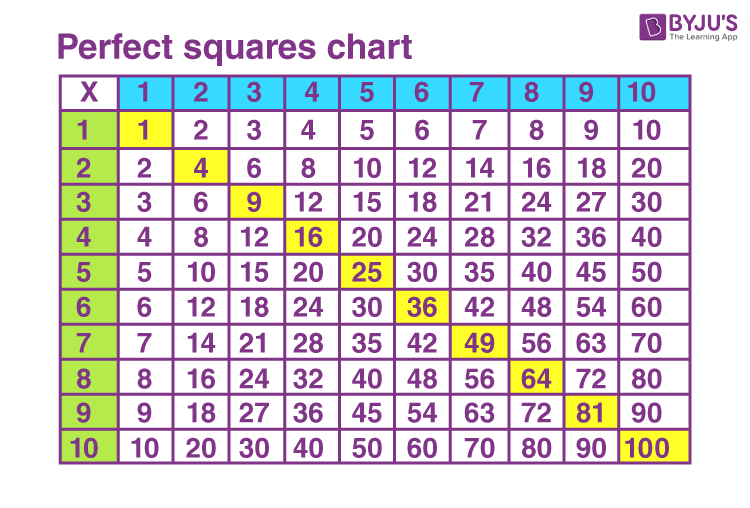
Examples of Squaring Different Types of Numbers
Squaring different types of numbers involves multiplying the number by itself. Here, we provide examples of squaring various types of numbers to illustrate the concept.
1. Squaring Whole Numbers
- \(2^2 = 4\)
- \(5^2 = 25\)
- \(10^2 = 100\)
2. Squaring Integers
- \((-3)^2 = 9\)
- \((-7)^2 = 49\)
- \(6^2 = 36\)
3. Squaring Fractions
- \(\left(\frac{1}{2}\right)^2 = \frac{1}{4}\)
- \(\left(\frac{3}{4}\right)^2 = \frac{9}{16}\)
- \(\left(\frac{5}{6}\right)^2 = \frac{25}{36}\)
4. Squaring Decimals
- \(0.5^2 = 0.25\)
- \(1.2^2 = 1.44\)
- \(2.5^2 = 6.25\)
5. Squaring Negative Numbers
- \((-1)^2 = 1\)
- \((-4)^2 = 16\)
- \((-0.7)^2 = 0.49\)
These examples show that squaring a number always results in a non-negative value, regardless of whether the original number is positive, negative, a fraction, or a decimal.
Real-world Applications of Squared Numbers
Squared numbers, represented as \( b^2 \), have numerous applications in various fields. Here are some key examples:
- Geometry: In geometry, squaring is used to calculate the area of squares and other shapes. For instance, the area \( A \) of a square with side length \( b \) is given by \( A = b^2 \). This principle is also applied in the Pythagorean theorem to determine the lengths of sides in right triangles.
- Physics: Squared numbers are used to calculate physical quantities like energy. For example, in the equation for kinetic energy \( E_k = \frac{1}{2}mv^2 \), the velocity \( v \) is squared.
- Finance: In finance, the volatility of stocks is often measured using the variance and standard deviation, which involve squaring deviations from the mean. This helps in assessing the risk associated with investments.
- Engineering: Squared terms are crucial in engineering for calculating load, stress, and other factors in structural analysis. For instance, the moment of inertia, which is essential in beam bending calculations, is proportional to the square of the distance from the axis.
- Computer Graphics: Squaring is used in graphics algorithms for tasks such as distance calculation between points. For example, the distance \( d \) between two points \((x_1, y_1)\) and \((x_2, y_2)\) is given by \( d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \).
- Statistics: In statistics, squared numbers are used to compute variance and standard deviation, which measure the spread of data points in a dataset. The variance is the average of the squared differences from the mean.
- Construction: Squaring is used in construction to ensure accuracy and precision. For instance, builders use squared numbers to create right angles and calculate areas for materials and spaces.
These applications demonstrate the versatility and importance of squared numbers in solving real-world problems across different domains.
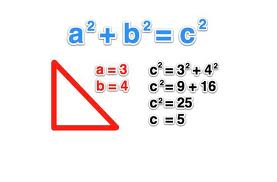
Squared Numbers in Geometry
In geometry, squared numbers play a significant role in various theorems and applications. One of the most well-known geometric interpretations involving squared numbers is the Pythagorean Theorem, which relates the sides of a right triangle.
The Pythagorean Theorem states that in a right triangle, the square of the hypotenuse (\( c \)) is equal to the sum of the squares of the other two sides (\( a \) and \( b \)). This can be expressed as:
\( a^2 + b^2 = c^2 \)
Here's how squared numbers are used in different geometric contexts:
- Pythagorean Theorem: This theorem helps in finding the length of any side of a right triangle when the lengths of the other two sides are known. It is foundational in Euclidean geometry and is used in various applications, such as construction and navigation.
- Distance Formula: In coordinate geometry, the distance between two points \((x_1, y_1)\) and \((x_2, y_2)\) is calculated using the Pythagorean Theorem. The formula is:
\( \text{Distance} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \)
- Area of Squares and Rectangles: The area of a square is simply the side length squared (\( s^2 \)), and the area of a rectangle can be found using the product of its length and width, which involves squaring if the sides are equal.
\( \text{Area of a square} = s^2 \)
- Circle Geometry: Squared numbers appear in the formulas for the area and circumference of a circle. For instance, the area of a circle is \(\pi r^2\), where \( r \) is the radius.
\( \text{Area of a circle} = \pi r^2 \)
- Volume Calculations: For three-dimensional shapes, such as cubes and spheres, squared numbers are used alongside cubed numbers. For a cube, the volume is \( s^3 \), and for a sphere, the volume involves the radius squared in the formula \( \frac{4}{3} \pi r^3 \).
Overall, squared numbers are integral to understanding and solving geometric problems, providing a link between algebra and geometry that enables the calculation of distances, areas, and volumes.
Physics Applications of Squared Numbers
Squared numbers, such as \( b^2 \), play a significant role in various physics applications. Understanding these applications can provide insight into how mathematical concepts are used to describe and predict physical phenomena.
Kinetic Energy
Kinetic energy (\(\text{KE}\)) of an object is given by the equation:
\[ \text{KE} = \frac{1}{2} mv^2 \]
Here, \( m \) is the mass of the object, and \( v \) is its velocity. The term \( v^2 \) highlights how kinetic energy increases with the square of the velocity. This means that if the velocity of an object doubles, its kinetic energy increases by a factor of four.
Work-Energy Theorem
The work-energy theorem states that the net work done on an object is equal to its change in kinetic energy:
\[ W_{\text{net}} = \Delta \text{KE} = \frac{1}{2} mv^2 - \frac{1}{2} mv_0^2 \]
In this context, the squared velocity term (\( v^2 \)) indicates the importance of the velocity in determining the kinetic energy change due to work done on the object.
Equations of Motion
In kinematics, the equations of motion for constant acceleration involve squared terms. For instance, the relationship between displacement (\( s \)) and velocity (\( v \)) is given by:
\[ v^2 = v_0^2 + 2a(s - s_0) \]
Where \( v_0 \) is the initial velocity, \( a \) is the acceleration, and \( s_0 \) is the initial position. This equation shows how the final velocity squared (\( v^2 \)) depends on the initial velocity squared (\( v_0^2 \)), acceleration, and displacement.
Gravitational Potential Energy
In gravitational fields, potential energy and related concepts often involve squared terms. For example, the escape velocity (\( v_e \)) of an object from a planet's gravitational field is derived from the energy required to overcome the gravitational pull:
\[ v_e = \sqrt{\frac{2GM}{r}} \]
Where \( G \) is the gravitational constant, \( M \) is the mass of the planet, and \( r \) is the radius from the center of the planet. The squared term appears when considering the kinetic energy needed for an object to escape the gravitational influence.
Driving Safety
In practical terms, the concept of squared numbers is essential in understanding driving safety. For example, the stopping distance of a vehicle is proportional to the square of its speed. Doubling the speed of a car results in a fourfold increase in the stopping distance, emphasizing the exponential increase in risk with higher speeds.
These examples illustrate the fundamental role of squared numbers in various physical concepts and equations, demonstrating their importance in both theoretical and practical applications.
Statistics and Squared Numbers
In statistics, squared numbers play a vital role in various analyses and tests. Here are some of the key applications:
Variance and Standard Deviation
Variance is a measure of the dispersion of a set of values. It is calculated by taking the average of the squared differences from the mean. The formula for variance \( \sigma^2 \) is:
\[
\sigma^2 = \frac{1}{N}\sum_{i=1}^{N}(x_i - \mu)^2
\]
where \( x_i \) represents each value in the dataset, \( \mu \) is the mean of the values, and \( N \) is the number of values.
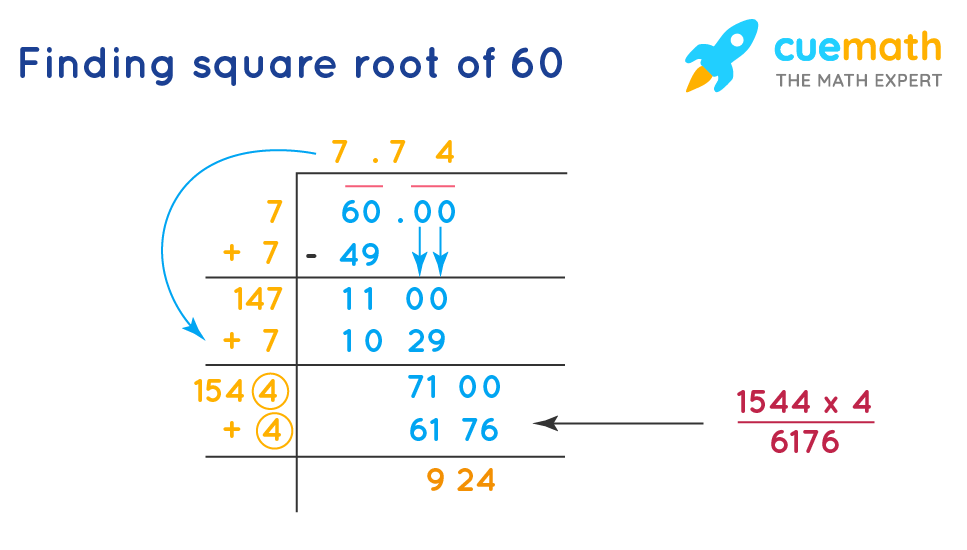
Standard deviation is the square root of the variance:
\[
\sigma = \sqrt{\sigma^2}
\]
It provides a measure of the average distance from the mean, offering a more interpretable measure of dispersion than variance.
Chi-Square Tests
Chi-square tests are used to determine whether there is a significant association between categorical variables. There are two main types of chi-square tests:
- Chi-Square Goodness of Fit Test: This test determines if a sample data matches a population with a specific distribution.
- Chi-Square Test of Independence: This test assesses whether two categorical variables are independent.
The chi-square test statistic is calculated as follows:
\[
\chi^2 = \sum \frac{(O - E)^2}{E}
\]
where \( O \) represents the observed frequency and \( E \) is the expected frequency.
The resulting chi-square statistic follows a chi-square distribution, which depends on the degrees of freedom. The degrees of freedom are determined by the number of categories in the variables being tested.
Regression Analysis
In regression analysis, the coefficient of determination \( R^2 \) is used to indicate how well data fit a statistical model. It is calculated by squaring the correlation coefficient:
\[
R^2 = \left( \frac{\text{Cov}(X, Y)}{\sigma_X \sigma_Y} \right)^2
\]
where Cov(X, Y) is the covariance of variables X and Y, and \( \sigma_X \) and \( \sigma_Y \) are their standard deviations. The \( R^2 \) value ranges from 0 to 1, with higher values indicating a better fit.
Sum of Squares
The sum of squares is a fundamental concept in ANOVA (Analysis of Variance) and other statistical tests. It measures the total variation within a dataset. It is calculated as:
\[
\text{Total Sum of Squares} (SS_{Total}) = \sum (x_i - \bar{x})^2
\]
where \( x_i \) represents individual data points and \( \bar{x} \) is the mean of the data.
In ANOVA, the total sum of squares is partitioned into the sum of squares between groups (SS_{Between}) and the sum of squares within groups (SS_{Within}), helping to determine if there are significant differences between group means.
Conclusion
Squared numbers are integral to various statistical methods and tests. From measuring variability with variance and standard deviation to evaluating model fit with \( R^2 \), and testing hypotheses with chi-square tests, squared numbers provide essential tools for interpreting and analyzing data.
Common Mistakes and Misconceptions
When working with squared numbers, there are several common mistakes and misconceptions that can lead to errors. Understanding these pitfalls is crucial for mastering the concept of squaring numbers.
-
Misinterpreting the Order of Operations:
One of the most common mistakes is not following the correct order of operations. For example, \( -b^2 \) is often incorrectly calculated as \( (-b)^2 \). The correct interpretation is \( -(b^2) \), which means you first square \( b \) and then apply the negative sign.
-
Forgetting Both Positive and Negative Solutions:
When solving equations like \( b^2 = 25 \), it's important to remember that there are two solutions: \( b = 5 \) and \( b = -5 \). Neglecting the negative solution is a common error.
-
Incorrectly Simplifying Expressions:
Another frequent mistake is incorrectly simplifying expressions that involve squared terms. For instance, \( (x-5)^2 \) should be expanded as \( x^2 - 10x + 25 \), but it is often mistakenly simplified to \( x^2 - 25 \).
-
Misunderstanding Squaring of Negative Numbers:
It's essential to correctly handle the squaring of negative numbers. For example, \( (-5)^2 = 25 \), not \( -25 \). The negative sign is part of the base being squared.
-
Confusion with Distributive Property:
Misapplying the distributive property can lead to errors. For instance, \( (a + b)^2 \) is not equal to \( a^2 + b^2 \). The correct expansion is \( a^2 + 2ab + b^2 \).
Understanding these common mistakes and misconceptions is vital for accurately working with squared numbers and avoiding errors in calculations and algebraic manipulations.

Advanced Concepts Related to Squaring Numbers
Squaring numbers is a fundamental mathematical operation with numerous advanced applications in various fields. Understanding these advanced topics can deepen your mathematical knowledge and open up new areas of study and application.
- Algebraic Identities:
Squaring plays a crucial role in algebraic identities, such as the difference of squares and binomial formulas. These identities are foundational in solving algebraic equations and manipulating expressions.
For example, the difference of squares identity is given by:
\[(a^2 - b^2 = (a + b)(a - b))\]
The binomial square formulas are:
\[(a + b)^2 = a^2 + 2ab + b^2\]
\[(a - b)^2 = a^2 - 2ab + b^2\]
- Quadratic Equations:
Quadratic equations, which are of the form \(ax^2 + bx + c = 0\), often involve squaring. Solutions to these equations frequently require the use of the square root principle, demonstrating the close relationship between squaring and square roots in algebra.
- Calculus:
In calculus, squaring functions is essential for defining the curvature of graphs, calculating areas under curves, and determining moments of inertia in physics. The operation of squaring is also crucial in finding the variance in statistics, which measures dispersion.
- Complex Numbers:
Squaring is significant in the field of complex numbers, especially when calculating the modulus of a complex number. The modulus is the square root of the sum of the squares of its real and imaginary parts, which is essential for understanding the geometric representation of complex numbers.
- Geometry and Trigonometry:
In geometry, the Pythagorean theorem is a classic example of squaring, relating the lengths of the sides of a right triangle:
\[a^2 + b^2 = c^2\]
In trigonometry, squaring is used in formulas involving sine, cosine, and tangent functions.
- Cryptography:
In cryptography, squaring numbers plays a role in various encryption algorithms and protocols. Understanding how squaring works is fundamental to grasping more complex cryptographic methods.
These advanced concepts highlight the importance of squaring in various mathematical and practical applications, showcasing its integral role in both basic and complex calculations.
Conclusion and Further Reading
In conclusion, understanding \( b^2 \) (b squared) is fundamental in various fields of mathematics and its applications. From basic arithmetic to advanced statistics, the concept of squaring a number plays a crucial role. Whether we are dealing with geometric interpretations, algebraic manipulations, or real-world applications, the power of squared numbers is evident.
Throughout this guide, we have explored the definition, properties, and applications of squared numbers. We've also delved into the common mistakes and misconceptions, advanced concepts, and their significance in statistics. Understanding these elements allows us to appreciate the depth and breadth of mathematics, making us better equipped to handle complex problems.
For further reading and to deepen your understanding of squared numbers and their applications, consider exploring the following resources:
These resources will provide you with comprehensive insights and help you further explore the intriguing world of squared numbers. Happy learning!
B Squared Được Đánh Giá Bởi SENsible SENCO