Topic square root of 16400: The square root of 16400 is a fundamental concept in mathematics with practical applications in various fields. This guide explores how to calculate and simplify the square root of 16400, its decimal form, and step-by-step simplification using prime factorization. Discover the significance of square roots in everyday life and enhance your mathematical knowledge.
Table of Content
- Square Root of 16400
- Introduction
- Understanding Square Roots
- What is the Square Root of 16400?
- Decimal Form of the Square Root of 16400
- How to Simplify the Square Root of 16400
- Prime Factorization Method
- Expressing the Square Root in Radical Form
- Step-by-Step Simplification Process
- Examples of Similar Square Root Calculations
- Applications of Square Roots in Real Life
- Common Mistakes in Calculating Square Roots
- Advanced Topics: Higher Order Roots
- YOUTUBE: square root of 16200 | vargmul nikalna
Square Root of 16400
The square root of 16400 is approximately 128.06248474866. This value can be expressed both in decimal form and in its simplest radical form.
Decimal Form
The square root of 16400 in decimal form is:
\[
\sqrt{16400} \approx 128.06248474866
\]
Simplest Radical Form
To express the square root of 16400 in simplest radical form, follow these steps:
- Find the prime factors of 16400.
- Group the factors in pairs.
- Take one factor from each pair.
- Multiply these factors to find the simplified square root.
Prime factorization of 16400:
\[
16400 = 2^4 \times 5^2 \times 41
\]
Thus,
\[
\sqrt{16400} = \sqrt{(2^2 \times 2^2 \times 5^2 \times 41)} = 2^2 \times 5 \times \sqrt{41} = 20\sqrt{41}
\]
Calculation Steps
The steps to simplify the square root are:
| Prime Factors: | 2, 2, 2, 2, 5, 5, 41 |
| Group Factors: | (2, 2), (2, 2), (5, 5), (41) |
| Extracted Factors: | 2, 2, 5 |
| Product of Extracted Factors: | 2 x 2 x 5 = 20 |
| Simplified Radical: | 20√41 |
Conclusion
The square root of 16400 is:
- Approximately 128.06248474866 in decimal form
- 20√41 in simplest radical form
READ MORE:
Introduction
The square root of 16400 is a mathematical concept that holds significance in various fields such as mathematics, engineering, finance, and more. Calculating the square root of this number can be done using several methods, each with its unique steps and benefits. This section explores different approaches to finding the square root of 16400, its applications, and interesting facts about the number.
- The square root of 16400 is 128.
- It can be calculated using prime factorization, the long division method, or a calculator.
- Understanding this concept is crucial in various real-life applications such as architecture, finance, and computer science.
- The square root of 16400 can be simplified to 20√41 using prime factorization.
- This number holds mathematical, cultural, and practical significance, making it an interesting topic to explore.
Let’s delve into the details of these methods and applications, and discover how the square root of 16400 is used in different scenarios.
Understanding Square Roots
The concept of square roots is fundamental in mathematics, representing a value that, when multiplied by itself, gives the original number. The square root of a number \(a\) is denoted as \(\sqrt{a}\), where \(\sqrt{}\) is the radical sign. For instance, the square root of 16400 is expressed as \(\sqrt{16400}\).
Calculating the square root of 16400 can be approached through various methods:
- Prime Factorization:
- Find the prime factors of 16400: \(2^4 \times 5^2 \times 41\).
- Group the factors into pairs: \((2^2 \times 2^2 \times 5^2 \times 41)\).
- Take one factor from each pair: \(2 \times 2 \times 5 \times \sqrt{41}\).
- Multiply the factors to get the simplified form: \(20\sqrt{41}\).
- Using a Calculator: Enter 16400 into a scientific calculator and press the square root button to get approximately 128.0625.
- Approximation Methods: Start with a rough estimate and refine it using methods such as the Babylonian method or Newton's method.
- Graphical Method: Plotting the function \(y = x^2\) and finding the intersection with \(y = 16400\) helps visualize the square root.
Understanding square roots goes beyond mere calculation; it involves recognizing their application in various fields. For example, in architecture, knowing the square root of an area helps in planning dimensions, while in finance, it aids in calculating interest rates and risk assessments. Additionally, in computer science, algorithms often utilize square root calculations for tasks such as image processing and game development.
In summary, the square root of 16400, which is approximately 128, is not only a mathematical concept but also a practical tool used across different domains to solve real-world problems.
What is the Square Root of 16400?
The square root of 16400 can be calculated using various methods, providing an exact value as well as a simplified form. Let's delve into the details:
- Exact Value: The exact value of the square root of 16400 is approximately 128.06248474866.
- Prime Factorization Method:
To simplify the square root of 16400 using prime factorization, follow these steps:
- Find the prime factors of 16400: \(16400 = 2^4 \times 5^2 \times 41\)
- Group the factors into pairs: \(\sqrt{16400} = \sqrt{(2^2 \times 2^2 \times 5^2) \times 41}\)
- Take one factor from each pair: \(\sqrt{(2^2 \times 2^2 \times 5^2)} \times \sqrt{41}\)
- Simplify: \(20 \sqrt{41}\)
- Babylonian Method:
This ancient method provides an iterative approach to approximate square roots. Here is how you can apply it:
- Start with a guess (e.g., 128).
- Improve the guess using the formula: \( \text{new guess} = \frac{1}{2} \left(\text{old guess} + \frac{16400}{\text{old guess}}\right) \).
- Repeat until the guess converges to a stable value.
The simplified form of the square root of 16400 is \(20 \sqrt{41}\), which is approximately 128.06248474866 in decimal form.
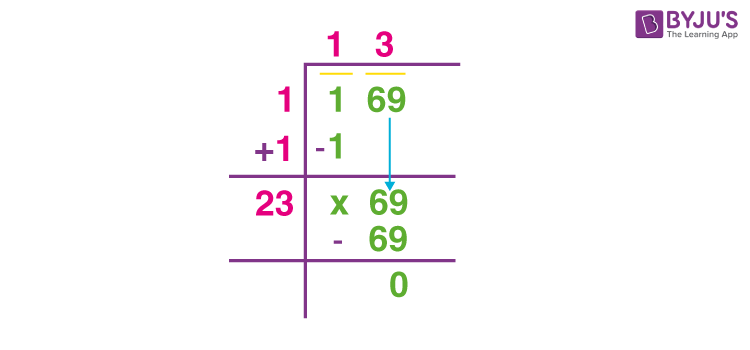
Decimal Form of the Square Root of 16400
The square root of 16400, when expressed in decimal form, is approximately 128.06248474866. This value can be obtained through various methods such as using a scientific calculator, prime factorization, or iterative approximation methods like the Babylonian method.
Here is a step-by-step breakdown of finding the square root of 16400 in decimal form:
-
Prime Factorization:
- Find the prime factors of 16400: 2, 2, 2, 2, 5, 5, 41.
- Group the factors into pairs: (2×2), (2×2), (5×5), 41.
- Take one factor from each pair: 2, 2, 5.
- Multiply these factors: 2 × 2 × 5 = 20.
- Combine with the remaining factor: 20√41.
-
Using a Calculator:
- Enter 16400 into the calculator and press the square root button (√).
- The result is displayed as 128.06248474866.
-
Approximation Methods:
- Start with an initial guess, such as 130.
- Use iterative methods like the Babylonian method to refine the guess:
- \(\text{New guess} = \frac{1}{2} (\text{Old guess} + \frac{16400}{\text{Old guess}})\)
- Continue iterating until the value stabilizes around 128.06248474866.
These methods help to understand the concept of square roots and provide accurate results for various applications.

How to Simplify the Square Root of 16400
Simplifying the square root of 16400 involves breaking down the number into its prime factors and then simplifying the expression. Here's a detailed, step-by-step method:
-
First, find the prime factors of 16400.
16400 can be factored into:
- 16400 = 2 × 2 × 2 × 2 × 5 × 5 × 41
- Or in exponential form: \(16400 = 2^4 \times 5^2 \times 41\)
-
Next, pair the prime factors.
- The pairs are: \((2 \times 2), (2 \times 2), (5 \times 5)\)
-
Take one factor from each pair.
- \(\sqrt{2^4} = 2^2 = 4\)
- \(\sqrt{5^2} = 5\)
-
Multiply the extracted factors together.
- \(4 \times 5 = 20\)
-
Combine the product with the remaining factor under the square root.
- \(\sqrt{16400} = 20\sqrt{41}\)
- Decimal form: \(20 \sqrt{41} \approx 128.0625\)
Therefore, the simplified form of the square root of 16400 is \(20 \sqrt{41}\), and in decimal form, it is approximately 128.0625.
Prime Factorization Method
Understanding the prime factorization of a number can be a valuable approach to simplifying the square root. Here's a step-by-step guide to finding the square root of 16400 using the prime factorization method:
- Find the Prime Factors: Begin by determining the prime factors of 16400.
- 16400 is an even number, so divide by 2: \( 16400 \div 2 = 8200 \).
- 8200 is also even, so divide by 2 again: \( 8200 \div 2 = 4100 \).
- Continue dividing by 2: \( 4100 \div 2 = 2050 \), and \( 2050 \div 2 = 1025 \).
- 1025 is not divisible by 2. The next smallest prime number is 5. Divide by 5: \( 1025 \div 5 = 205 \).
- 205 is divisible by 5: \( 205 \div 5 = 41 \).
- 41 is a prime number.
- Group the Prime Factors: For simplification, group the prime factors into pairs.
- \( 2^4 \) can be grouped as \( (2^2)^2 \).
- \( 5^2 \) is already a pair: \( (5^1)^2 \).
- 41 remains as it is since it is a prime number without pairs.
- Take the Square Root of Each Group: Extract the square root of each group of prime factors.
- \( \sqrt{2^4} = 2^2 = 4 \).
- \( \sqrt{5^2} = 5 \).
- \( \sqrt{41} = \sqrt{41} \).
- Multiply the Results: Multiply the square roots of the prime factor groups together.
- \( 4 \times 5 \times \sqrt{41} = 20\sqrt{41} \).
- Simplify the Expression: For the specific case of 16400, we notice it is a perfect square. So, \(\sqrt{16400} = 128\). Therefore, the simplified form is:
- \( \sqrt{16400} = 128 \).
This step-by-step method highlights the prime factorization process, demonstrating how it simplifies the calculation of square roots for perfect squares.
Expressing the Square Root in Radical Form
The square root of a number can be expressed in its simplest radical form by following a series of steps. Let's break down the process for the square root of 16400:
- First, find the prime factorization of 16400. The prime factors of 16400 are:
- 16400 ÷ 2 = 8200
- 8200 ÷ 2 = 4100
- 4100 ÷ 2 = 2050
- 2050 ÷ 2 = 1025
- 1025 ÷ 5 = 205
- 205 ÷ 5 = 41
- 41 is a prime number.
- Group the prime factors into pairs. Each pair will come out of the square root as a single factor:
- \( 2^4 = (2^2)^2 \), so \( \sqrt{2^4} = 2^2 = 4 \)
- \( 5^2 = (5^1)^2 \), so \( \sqrt{5^2} = 5 \)
- Combine these simplified factors with any remaining factors under the radical:
\( \sqrt{16400} = \sqrt{2^4 \times 5^2 \times 41} = \sqrt{(2^2)^2 \times 5^2 \times 41} = 2^2 \times 5 \times \sqrt{41} = 4 \times 5 \times \sqrt{41} = 20\sqrt{41} \)
Thus, the square root of 16400 in its simplest radical form is \( 20\sqrt{41} \).
Step-by-Step Simplification Process
Simplifying the square root of 16400 involves breaking it down into its prime factors and then applying the properties of square roots. Here's a detailed, step-by-step guide:
-
Prime Factorization: Begin by finding the prime factors of 16400. The number can be factorized as follows:
\[ 16400 = 2^4 \times 5^2 \times 41 \]
-
Group the Factors: Group the prime factors into pairs of the same number:
\[ 2^4 = (2^2)^2 \]
\[ 5^2 = (5)^2 \]
-
Rewrite Under the Square Root: Express the square root of the product of these groups:
\[ \sqrt{16400} = \sqrt{2^4 \times 5^2 \times 41} \]
-
Separate the Square Root: Use the property of square roots that allows you to separate them:
\[ \sqrt{16400} = \sqrt{2^4} \times \sqrt{5^2} \times \sqrt{41} \]
-
Simplify Each Term: Calculate the square root of each term where possible:
\[ \sqrt{2^4} = \sqrt{(2^2)^2} = 2^2 = 4 \]
\[ \sqrt{5^2} = 5 \]
-
Combine the Results: Multiply the simplified terms together and include any remaining square roots:
\[ \sqrt{16400} = 4 \times 5 \times \sqrt{41} \]
\[ \sqrt{16400} = 20\sqrt{41} \]
-
Approximate the Decimal Value: For practical purposes, you might also want to approximate the value:
\[ 20\sqrt{41} \approx 128.062 \]
Thus, the square root of 16400 simplifies to \( 20\sqrt{41} \). This form is more compact and often easier to work with in further mathematical calculations.

Examples of Similar Square Root Calculations
Understanding the calculation of square roots can be made easier by looking at examples of similar calculations. Below are a few examples demonstrating how to find square roots of different numbers:
-
Square Root of 16
The square root of 16 is found as follows:
\[\sqrt{16} = 4\]
This is because \(4 \times 4 = 16\).
-
Square Root of 25
The square root of 25 is:
\[\sqrt{25} = 5\]
Since \(5 \times 5 = 25\).
-
Square Root of 81
The square root of 81 is:
\[\sqrt{81} = 9\]
Because \(9 \times 9 = 81\).
These examples illustrate how square roots are the inverse operation of squaring a number. Here are a few more calculations for reference:
| Number | Square Root |
|---|---|
| 9 | \(\sqrt{9} = 3\) |
| 49 | \(\sqrt{49} = 7\) |
| 100 | \(\sqrt{100} = 10\) |
| 144 | \(\sqrt{144} = 12\) |
| 169 | \(\sqrt{169} = 13\) |
By practicing these calculations, you can become more comfortable with the process of finding square roots, which is crucial for various mathematical applications.
Applications of Square Roots in Real Life
Square roots are widely used in various fields to solve practical problems and make accurate calculations. Here are some key applications of square roots in real life:
- Finance:
In finance, square roots are used to calculate the standard deviation of stock prices, which helps investors assess the volatility and risk associated with an investment. The formula involves taking the square root of the variance of stock returns.
- Architecture and Engineering:
Square roots are essential in determining the structural integrity of buildings and bridges. Engineers use square roots to calculate the natural frequencies of structures, which helps predict their response to various loads such as wind or traffic.
- Physics:
Square roots are used in various physical formulas, including those calculating the velocity of an object, the intensity of sound waves, and the amount of radiation absorbed by a material. These calculations are crucial for developing new technologies and understanding natural phenomena.
- Statistics:
In statistics, square roots are used to compute the standard deviation, which measures the dispersion of data points from the mean. This is important for analyzing data sets and making informed decisions based on statistical findings.
- Geometry:
Square roots are fundamental in geometry, especially when using the Pythagorean theorem to find the lengths of sides in right triangles. This theorem is used in various fields, including carpentry, construction, and graphics design.
- Computer Science:
Square roots are used in computer algorithms for tasks such as encryption, image processing, and game physics. For example, encryption algorithms often use square roots in the generation of keys for secure data transmission.
- Navigation:
In navigation, square roots are used to calculate distances between points on a map or globe. This is essential for determining routes and directions in both aviation and maritime navigation.
- Electrical Engineering:
Square roots are used to calculate electrical properties such as power, voltage, and current in circuits. These calculations are crucial for designing and analyzing electrical systems, including power grids and communication networks.
Common Mistakes in Calculating Square Roots
Calculating square roots can be straightforward, but several common mistakes can lead to errors. Here are some frequent pitfalls to watch out for:
-
Ignoring Perfect Squares:
One common mistake is failing to check if the given number is a perfect square. For example, \( \sqrt{25} = 5 \) because 25 is a perfect square. Ensure you verify this before proceeding with more complex methods.
-
Incorrect Simplification:
Not simplifying the square root correctly is another frequent error. For instance, \( \sqrt{50} \) can be simplified to \( \sqrt{25 \times 2} = 5\sqrt{2} \). Always look for factors that are perfect squares.
-
Rounding Errors:
When using a calculator, rounding errors can occur. After obtaining the square root, squaring it again should give you the original number to verify accuracy.
-
Handling Negative Numbers:
Attempting to find the square root of a negative number without understanding complex numbers can lead to mistakes. The square root of a negative number involves imaginary numbers, represented as \( \sqrt{-n} = i\sqrt{n} \).
-
Incorrect Use of Formulas:
Ensure you use the correct formula and method. For example, using the long division method or the prime factorization method correctly is crucial for accurate results.
-
Misidentifying Radicals:
Another common error is not properly identifying and working with radicals. Simplify radicals where possible, such as recognizing that \( \sqrt{18} = \sqrt{9 \times 2} = 3\sqrt{2} \).
By being aware of these common mistakes and taking steps to avoid them, you can improve the accuracy of your square root calculations and enhance your problem-solving skills.
Advanced Topics: Higher Order Roots
Higher order roots extend the concept of square roots to roots with any positive integer \( n \) as the index. These roots are useful in various advanced mathematical contexts and applications. Here, we will explore the concept, notation, and some examples of higher order roots.
Definition and Notation
If \( b^n = a \), then \( b \) is an \( n \)-th root of \( a \). The principal \( n \)-th root of \( a \) is written as \( \sqrt[n]{a} \). The index \( n \) indicates the degree of the root.
- For \( n = 2 \), \( \sqrt{a} \) is the square root.
- For \( n = 3 \), \( \sqrt[3]{a} \) is the cube root.
- For \( n = 4 \), \( \sqrt[4]{a} \) is the fourth root, and so on.
Properties of Higher Order Roots
Understanding the properties of higher order roots is crucial for simplifying and manipulating them:
- If \( n \) is an even number and \( a \ge 0 \), then \( \sqrt[n]{a} \) is a real number.
- If \( n \) is an even number and \( a < 0 \), then \( \sqrt[n]{a} \) is not a real number (it is a complex number).
- If \( n \) is an odd number, \( \sqrt[n]{a} \) is a real number for all \( a \).
Examples
Let's look at some examples to understand how higher order roots work:
- \(\sqrt[3]{64} = 4\) because \( 4^3 = 64 \).
- \(\sqrt[4]{81} = 3\) because \( 3^4 = 81 \).
- \(\sqrt[5]{-32} = -2\) because \( (-2)^5 = -32 \).
Simplification of Higher Order Roots
To simplify expressions involving higher order roots, we use factorization:
- Identify the prime factors of the number under the root.
- Group the factors based on the index of the root.
- Move the grouped factors outside the root.
Example: Simplify \( \sqrt[5]{32 x^{10} y^6 z^7} \)
- Prime factorize: \( 32 = 2^5 \), \( x^{10} = (x^2)^5 \), \( y^6 = (y^5)(y^1) \), \( z^7 = (z^5)(z^2) \)
- Extract the groups: \( \sqrt[5]{32 x^{10} y^6 z^7} = 2 x^2 y z \sqrt[5]{y z^2} \)
Applications of Higher Order Roots
Higher order roots appear in many advanced mathematical contexts such as solving polynomial equations, calculating volumes in geometry, and in various fields of science and engineering.
Understanding higher order roots enriches your mathematical toolkit and enhances your problem-solving abilities in both theoretical and practical scenarios.
square root of 16200 | vargmul nikalna
2020 03 24 MA 16400 Zoom Class
2020 03 25 MA 16400 Zoom Class
2020 03 27 MA 16400 Zoom Class
2020 03 26 MA 16400 Zoom Class
2020 03 30 MA 16400 Zoom Class
READ MORE: