Square Root of 160: Simplified Explanation and Calculation Methods

The square root of 160 can be expressed in various forms. Here's a detailed explanation of its value, properties, and methods of calculation.

Exact and Approximate Values

• Decimal Form: \( \sqrt{160} \approx 12.649 \)
• Radical Form: \( \sqrt{160} = 4\sqrt{10} \)
• Exponential Form: \( 160^{1/2} \)

Prime Factorization Method

The prime factorization of 160 is:

• \( 160 = 2 \times 2 \times 2 \times 2 \times 2 \times 5 = 2^5 \times 5 \)
• Simplified form: \( \sqrt{160} = \sqrt{2^5 \times 5} = 4\sqrt{10} \)

Calculation Methods

1. Using Newton's Method

   Newton's equation for approximating the square root is:

   \( \sqrt{N} \approx \frac{1}{2} \left( \frac{N}{A} + A \right) \)

   Where \( N = 160 \) and \( A \approx 12 \):

   \( \sqrt{160} \approx \frac{1}{2} \left( \frac{160}{12} + 12 \right) = 12.66 \)

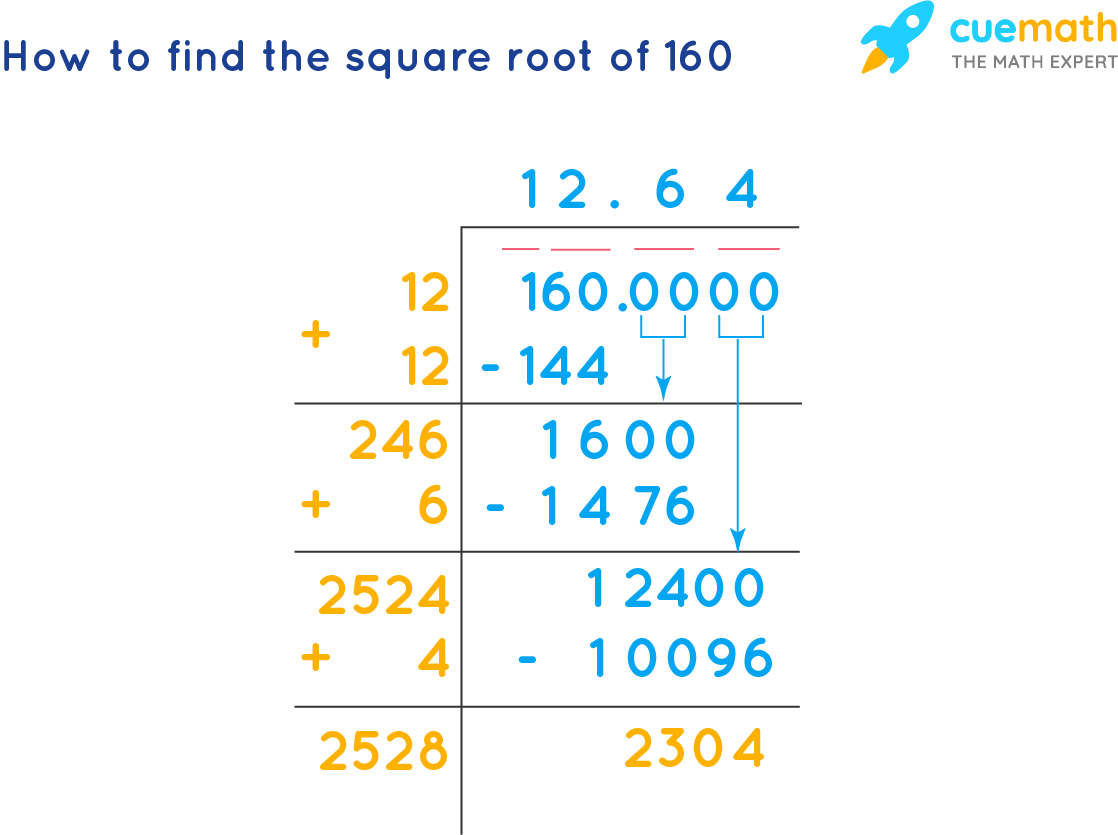
2. Using the Long Division Method

   The long division method helps find the square root of 160 by breaking it into manageable steps, yielding approximately 12.64.

Examples and Applications

• Example 1: Area of a Circle

  If the area of a circle is \( 160 \, \text{cm}^2 \), the radius \( r \) is:

  \( r = \sqrt{160} \approx 12.649 \, \text{cm} \)

• Example 2: Perimeter Calculation

  The perimeter of a circle with radius \( 12.649 \, \text{cm} \) is:

  \( P = 2 \pi r \approx 79.38 \, \text{cm} \)

Conclusion

In summary, the square root of 160 is an irrational number approximately equal to 12.649, commonly represented as \( 4\sqrt{10} \). It can be calculated through methods like prime factorization, Newton's method, and long division.

The concept of square roots is fundamental in mathematics, playing a crucial role in various fields such as algebra, geometry, and calculus. The square root of a number is a value that, when multiplied by itself, gives the original number. In this comprehensive guide, we will explore the square root of 160, a non-perfect square, through various methods and representations.

Understanding the square root of 160 involves delving into different mathematical techniques and approximations. This guide will provide a detailed examination of these methods, including prime factorization, Newton's approximation, and the long division method. We will also look at the properties of the square root of 160, its simplest radical form, and related mathematical problems.

By the end of this guide, you will have a thorough understanding of how to calculate and interpret the square root of 160, along with practical examples and challenging questions to test your knowledge. Whether you are a student, educator, or math enthusiast, this guide will serve as a valuable resource for mastering the concept of square roots.

The square root of 160 can be represented in multiple forms:

• Radical Form: √160
• Exponential Form: 160^½
• Decimal Form: ± 12.649110640673518 (approx.)

To better understand the square root of 160, let's break it down using prime factorization:

• The prime factorization of 160 is 2⁵ × 5.
• This allows us to simplify √160 as follows:
• √160 = √(2⁵ × 5) = √(2⁴ × 2 × 5)
• Using the property of square roots (√a × b = √a × √b):
• √160 = √(2⁴ × 10) = √(16 × 10)
• Since √16 = 4:
• √160 = 4√10

Using Newton's Method (also known as the Newton-Raphson method) for approximating square roots involves iterative calculation:

1. Start with an initial guess, x₀. For √160, we can use x₀ = 12.
2. Use the formula x_n+1 = (x_n + 160/x_n) / 2 to get closer to the actual square root.
3. First iteration: x₁ = (12 + 160/12) / 2 = 12.6667 (approx.)
4. Second iteration: x₂ = (12.6667 + 160/12.6667) / 2 ≈ 12.6491
5. Continue until the value stabilizes around 12.6491.

Another systematic method for finding the square root is the Long Division Method:

• Pair the digits of 160 from right to left: 1 | 60.
• Find the largest number whose square is less than or equal to the first pair (1). This is 1.
• Subtract 1² from 1 to get 0. Bring down the next pair (60) to get 60.
• Double the quotient (1) and find a digit (x) such that 2x × x ≤ 60. This is 2 (since 22 × 2 = 44).
• Subtract 44 from 60 to get 16. Bring down the next pair (00) to get 1600.
• Repeat the process to get closer to the exact decimal value.
• The approximate value obtained is 12.649.

There are several methods to calculate the square root of 160. Below, we explore three primary methods: Prime Factorization, Newton's Approximation, and Long Division.

Prime Factorization Method

The prime factorization method involves breaking down 160 into its prime factors and then simplifying the square root calculation.

• First, find the prime factors of 160: \(160 = 2^5 \times 5\).
• Then, simplify the square root: \( \sqrt{160} = \sqrt{2^5 \times 5} = \sqrt{2^4 \times 2 \times 5} = 4\sqrt{10} \).

So, the square root of 160 in its simplest radical form is \(4\sqrt{10}\).

Newton’s Approximation Method

Newton's method (also known as the Newton-Raphson method) provides an iterative approach to approximate the square root of a number. The formula used is:

\[ x_{n+1} = \frac{1}{2} \left( x_n + \frac{160}{x_n} \right) \]

Here’s how it works step-by-step:

1. Choose an initial guess, \(x_0\). For \( \sqrt{160} \), a reasonable starting point is \( x_0 = 12 \) (since \(12^2 = 144\), which is close to 160).
2. Apply the formula: \[ x_1 = \frac{1}{2} \left( 12 + \frac{160}{12} \right) \approx \frac{1}{2} \left( 12 + 13.33 \right) = \frac{25.33}{2} \approx 12.665 \]
3. Repeat the process with the new value to get a more accurate result. Typically, after a few iterations, the value converges to \( \sqrt{160} \approx 12.649 \).

Long Division Method

The long division method provides a systematic approach to finding the square root of a number by pairing digits and performing division and averaging:

• Pair the digits of 160 from right to left (16 | 00).
• Find the largest number whose square is less than or equal to 16 (which is 4, since \(4^2 = 16\)).
• Subtract 16 from 16 to get 0 and bring down the next pair of digits (00), making the number 00.
• Double the divisor (4) to get 8. Find a number (x) such that 8x times x is less than or equal to 0. Since we have no more digits to bring down, the approximate value of \( \sqrt{160} \) is 12.649.

Therefore, the square root of 160 calculated using the long division method is approximately 12.649.

To simplify the square root of 160, we follow a series of steps to find its simplest radical form:

1. Prime Factorization: First, we perform the prime factorization of 160. The prime factors of 160 are:

   \[160 = 2^5 \times 5\]

2. Grouping Factors: Next, we group the factors in pairs of two (since we're dealing with a square root):

   \[160 = (2^2 \times 2^2) \times 2 \times 5\]

3. Simplifying the Radical: We take out each pair of prime factors as a single number outside the radical:

   \[\sqrt{160} = \sqrt{(2^2 \times 2^2) \times 2 \times 5} = 2 \times 2 \times \sqrt{10} = 4\sqrt{10}\]

Therefore, the simplest radical form of \(\sqrt{160}\) is \(4\sqrt{10}\).

The square root of 160 has several important properties:

• Irrational Number: The square root of 160 is an irrational number. This means it cannot be expressed as a simple fraction of two integers, and its decimal representation is non-repeating and non-terminating.
• Positive and Negative Roots: The square root of 160 has both a positive and a negative value, expressed as ±√160. In decimal form, these values are approximately ±12.649.
• Non-Perfect Square: Since 160 is not a perfect square, its square root is not an integer. This is evident from its prime factorization which shows that 160 cannot be expressed as the square of any integer.
• Simplest Radical Form: The square root of 160 can be simplified to 4√10. This is derived by breaking down 160 into its prime factors: 160 = 2⁵ × 5, and simplifying accordingly.
• Imaginary Component: When considering negative roots, the square root of -160 is an imaginary number and is expressed as ±12.649i, where i represents the imaginary unit (√-1).

Understanding the square root of 160 allows us to tackle a variety of related mathematical problems. Here are some practical examples:

Example 1: Circle Radius

Suppose you need to find the radius of a circle with an area of 160π square units.

• Area of the circle: A = πr²
• Given: A = 160π
• To find the radius (r), solve: πr² = 160π
• Divide both sides by π: r² = 160
• Take the square root of both sides: r = √160 ≈ 12.649 units

Example 2: Area Calculation

Calculate the side length of a square with an area of 16000 square centimeters.

• Area of the square: A = s²
• Given: A = 16000 cm²
• To find the side length (s), solve: s² = 16000
• Take the square root of both sides: s = √16000 ≈ 126.49 cm

Example 3: Pythagorean Theorem

In a right triangle, if one leg is 10 units and the hypotenuse is 18 units, find the other leg (b).

• Pythagorean theorem: a² + b² = c²
• Given: a = 10 units, c = 18 units
• Substitute: 10² + b² = 18²
• Simplify: 100 + b² = 324
• Solve for b²: b² = 324 - 100 = 224
• Take the square root: b = √224 ≈ 14.97 units

Example 4: Rectangular Garden

A rectangular garden has an area of 160 square meters and one side of 8 meters. Find the length of the other side.

• Area of the rectangle: A = length × width
• Given: A = 160 m², width = 8 m
• To find the length (l), solve: 160 = l × 8
• Divide both sides by 8: l = 160 / 8 = 20 meters

Example 5: Volume of a Cube

Find the edge length of a cube with a volume of 160 cubic meters.

• Volume of the cube: V = s³
• Given: V = 160 m³
• To find the edge length (s), solve: s³ = 160
• Take the cube root: s = ∛160 ≈ 5.43 meters

Here are some challenging questions related to the square root of 160 that will help deepen your understanding:

• 1. What is the negative root of 160?

  The negative root of 160 is the negative counterpart of its positive square root. Hence, the negative root is:

  \[-\sqrt{160} \approx -12.649\]

• 2. Find the third root of 160.

  The third root (or cube root) of a number is a value that, when multiplied by itself three times, gives the original number. The cube root of 160 is:

  \[\sqrt[3]{160} \approx 5.429\]

• 3. Express 256 and 44100 in terms of the square root of 160.

  To express these numbers in terms of the square root of 160, we need to find a relationship between them and \(\sqrt{160}\):

  \[
  \begin{align*}
  256 &= 16^2 = (4\sqrt{10})^2 = (\sqrt{160})^2 \\
  44100 &= 210^2 = (21 \cdot 10 \cdot \sqrt{10})^2 = (21\sqrt{10})^2 = \left(\frac{21}{2}\sqrt{160}\right)^2
  \end{align*}
  \]

Is 160 a Perfect Square?

No, 160 is not a perfect square. A perfect square is a number that can be expressed as the square of an integer. Since the square root of 160 is an irrational number (approximately 12.649), it cannot be written as a simple fraction or an integer squared.

What is the Imaginary Root of 160?

The square root of -160 involves an imaginary number because you cannot take the square root of a negative number within the set of real numbers. The imaginary root of -160 is expressed as √-160 = 12.649i, where "i" is the imaginary unit (i.e., √-1).

What are the properties of the square root of 160?

• Irrational Number: The square root of 160 is an irrational number because it cannot be expressed as a simple fraction; its decimal form is non-terminating and non-repeating.
• Positive and Negative Roots: The square root of 160 has both positive and negative roots, ±12.649 (approximately).
• Radical Form: The simplest radical form of the square root of 160 is 4√10.

How do you calculate the square root of 160 using the long division method?

The long division method provides a step-by-step approach to find the square root of 160. Here's a brief outline:

1. Pair the digits of the number from right to left.
2. Find the largest number whose square is less than or equal to the first pair or single digit.
3. Subtract the square of the found number from the first pair and bring down the next pair of digits.
4. Double the current quotient and determine the next digit of the quotient which, when added and multiplied, gives a product less than or equal to the current number.
5. Continue the process until you reach the desired precision.

Using this method, √160 is approximately 12.649.

Is the square root of 160 rational or irrational?

The square root of 160 is an irrational number. This is because its decimal representation is non-terminating and non-repeating, and it cannot be expressed as a fraction of two integers.

How do you express the square root of 160 in exponential form?

The square root of 160 in exponential form is expressed as 160^½.

Can you simplify the square root of 160?

Yes, the square root of 160 can be simplified using its prime factorization. The prime factorization of 160 is 2⁵ × 5, which simplifies to 4√10 in radical form.

What is the relationship between the square root of 160 and other mathematical concepts?

• Quadratic Equations: The square root of 160 can be found as a solution to the quadratic equation x² - 160 = 0, which simplifies to x = ±√160.
• Geometry: The square root of 160 can be used to find the radius of a circle with an area of 160π square units, giving r = √160 ≈ 12.649 units.