Topic simplify square root of 36: Discover how to simplify the square root of 36 with our comprehensive guide. This article breaks down the process into easy-to-follow steps, ensuring you grasp the concept effortlessly. Whether you're a student or just curious about mathematics, you'll find this explanation clear and helpful. Simplify the square root of 36 with confidence!
Table of Content
- How to Simplify the Square Root of 36
- Introduction to Simplifying Square Roots
- Understanding Square Roots
- What is a Perfect Square?
- Steps to Simplify the Square Root of 36
- Verification of the Simplification
- Practical Applications of Simplifying Square Roots
- Common Mistakes and How to Avoid Them
- Additional Resources and Practice Problems
- YOUTUBE: Hướng dẫn cách đơn giản hóa căn bậc hai của 36 để thu hút người xem.
How to Simplify the Square Root of 36
The process of simplifying the square root of a number involves finding a number that, when multiplied by itself, gives the original number. Here, we simplify the square root of 36.
Step-by-Step Simplification
- Identify the number under the square root symbol: \( \sqrt{36} \).
- Determine if 36 is a perfect square. A perfect square is a number that has an integer as its square root.
- Find the integer that, when squared, equals 36: \( 6 \times 6 = 36 \).
- Conclude that the square root of 36 is 6: \( \sqrt{36} = 6 \).
Conclusion
Therefore, the simplified form of the square root of 36 is:
Verification
To verify, we can square the result to see if we get the original number:
Thus, our simplification is correct.

READ MORE:
Introduction to Simplifying Square Roots
Simplifying square roots is a fundamental skill in mathematics that involves expressing a square root in its simplest form. This process helps in making calculations easier and results more understandable. Below, we will explore the steps to simplify square roots, using the square root of 36 as an example.
Steps to Simplify Square Roots
- Identify the number under the square root symbol: \( \sqrt{n} \).
- Determine if the number is a perfect square. A perfect square has an integer as its square root.
- Find the integer whose square equals the given number.
- Express the square root in its simplest form.
Let's apply these steps to simplify the square root of 36:
- Identify the number under the square root: \( \sqrt{36} \).
- Check if 36 is a perfect square. Since \( 6 \times 6 = 36 \), 36 is indeed a perfect square.
- Find the integer whose square is 36, which is 6.
- Simplify the square root: \( \sqrt{36} = 6 \).
This process can be applied to any square root, making it easier to work with numbers in their simplest form.
Understanding Square Roots
A square root of a number is a value that, when multiplied by itself, gives the original number. It is one of the fundamental concepts in mathematics, and understanding it is crucial for simplifying square roots and solving various mathematical problems.
Definition and Notation
The square root of a number \( n \) is denoted as \( \sqrt{n} \). For example, the square root of 36 is written as \( \sqrt{36} \). This means we are looking for a number which, when squared, equals 36.
Perfect Squares
Some numbers are perfect squares, meaning their square roots are whole numbers. Examples of perfect squares include:
- \( 1 = 1 \times 1 \)
- \( 4 = 2 \times 2 \)
- \( 9 = 3 \times 3 \)
- \( 16 = 4 \times 4 \)
- \( 25 = 5 \times 5 \)
- \( 36 = 6 \times 6 \)
Non-Perfect Squares
For numbers that are not perfect squares, their square roots are not whole numbers and are often left in the square root form or approximated as decimal values. For example:
- \( \sqrt{2} \approx 1.414 \)
- \( \sqrt{3} \approx 1.732 \)
- \( \sqrt{5} \approx 2.236 \)
How to Find Square Roots
- Estimate: Find the two closest perfect squares between which your number lies.
- Refine: Use methods such as prime factorization or long division to find a more accurate value.
Understanding these concepts will help in simplifying square roots effectively. For instance, knowing that 36 is a perfect square and its square root is 6 helps simplify \( \sqrt{36} \) directly to 6.
What is a Perfect Square?
A perfect square is an integer that can be expressed as the product of an integer with itself. In other words, if \( n \) is a perfect square, then there exists an integer \( m \) such that \( n = m \times m \) or \( n = m^2 \). Perfect squares are important in simplifying square roots because they allow us to find exact integer results.
Examples of Perfect Squares
Here are some examples of perfect squares and their corresponding square roots:
- \( 1 = 1 \times 1 \) or \( 1^2 = 1 \)
- \( 4 = 2 \times 2 \) or \( 2^2 = 4 \)
- \( 9 = 3 \times 3 \) or \( 3^2 = 9 \)
- \( 16 = 4 \times 4 \) or \( 4^2 = 16 \)
- \( 25 = 5 \times 5 \) or \( 5^2 = 25 \)
- \( 36 = 6 \times 6 \) or \( 6^2 = 36 \)
- \( 49 = 7 \times 7 \) or \( 7^2 = 49 \)
- \( 64 = 8 \times 8 \) or \( 8^2 = 64 \)
- \( 81 = 9 \times 9 \) or \( 9^2 = 81 \)
- \( 100 = 10 \times 10 \) or \( 10^2 = 100 \)
Identifying Perfect Squares
- To identify a perfect square, check if the square root of the number is an integer.
- If the square root is an integer, the number is a perfect square. For example, \( \sqrt{36} = 6 \), so 36 is a perfect square.
- If the square root is not an integer, the number is not a perfect square. For example, \( \sqrt{20} \approx 4.472 \), so 20 is not a perfect square.
Importance of Perfect Squares in Simplifying Square Roots
Understanding perfect squares helps in simplifying square roots because it allows us to recognize when a square root can be simplified to an integer. For instance, knowing that 36 is a perfect square with a square root of 6 makes it easy to simplify \( \sqrt{36} \) to 6.
Steps to Simplify the Square Root of 36
To simplify the square root of 36, follow these detailed steps:
-
Recognize that 36 is a perfect square. A perfect square is a number that can be expressed as the product of an integer with itself. In this case, \( 36 = 6 \times 6 \).
-
Express the square root of 36 using the radical sign:
\[ \sqrt{36} \]
-
Since 36 is a perfect square, we can directly determine its square root. The square root of 36 is 6 because:
\[ 6 \times 6 = 36 \]
Thus,
\[ \sqrt{36} = 6 \]
-
Another way to simplify is by using the prime factorization method. Factor 36 into its prime factors:
\[ 36 = 2 \times 2 \times 3 \times 3 \]
-
Rewrite the prime factors using exponents:
\[ 36 = 2^2 \times 3^2 \]
-
Apply the square root to each prime factor:
\[ \sqrt{36} = \sqrt{2^2 \times 3^2} \]
Separate the factors under the square root:
\[ \sqrt{2^2} \times \sqrt{3^2} \]
-
Simplify each square root:
\[ \sqrt{2^2} = 2 \] and \[ \sqrt{3^2} = 3 \]
Therefore:
\[ \sqrt{36} = 2 \times 3 = 6 \]
Using these steps, we see that the square root of 36 is 6, which is the simplest form.
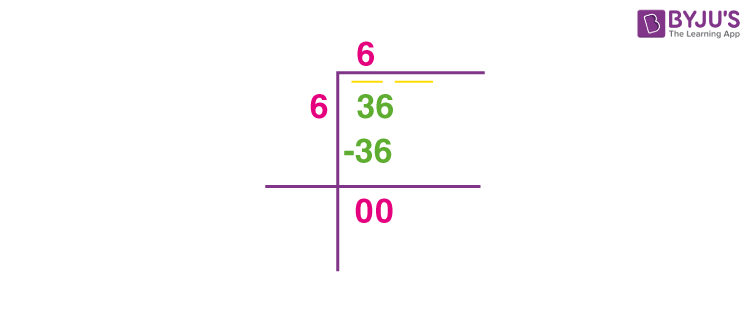
Verification of the Simplification
To verify the simplification of the square root of 36, we need to ensure that the steps and final result are correct. Here’s how we can verify it:
-
Original Expression:
We start with the original expression:
\(\sqrt{36}\)
-
Perfect Square Identification:
Identify if 36 is a perfect square. Since \(36 = 6^2\), we know that 36 is indeed a perfect square.
-
Simplification:
The square root of a perfect square is the base number:
\(\sqrt{36} = 6\)
-
Verification:
To verify the simplification, we can square the result to see if we get back the original number:
\(6^2 = 36\)
Since \(6^2 = 36\), the simplification \(\sqrt{36} = 6\) is correct.
-
Calculator Check:
Using a calculator, input \(\sqrt{36}\). The calculator should return 6, confirming our simplification.
-
Product Rule Confirmation:
We can also use the product rule for square roots to confirm:
\(\sqrt{36} = \sqrt{6 \cdot 6} = \sqrt{6^2} = 6\)
By following these steps, we can confidently verify that the simplification of the square root of 36 is indeed correct.
Practical Applications of Simplifying Square Roots
Simplifying square roots has many practical applications across various fields. Here are some examples:
- Finance: In finance, square roots are used to calculate stock market volatility, helping investors assess the risk of investments. For instance, the standard deviation, a measure of volatility, involves taking the square root of the variance.
- Architecture: Engineers use square roots to determine the natural frequency of structures like bridges and buildings, which is crucial for understanding how they will respond to loads such as wind and traffic.
- Science: Square roots are used in various scientific calculations, such as determining the velocity of moving objects, radiation absorption, and sound intensity.
- Statistics: In statistics, square roots are essential for calculating standard deviation, which measures how spread out numbers are from the mean in a data set.
- Geometry: Square roots are used to find distances in geometry, particularly in the Pythagorean theorem to solve for the lengths of sides in right triangles.
- Computer Science: In computer science, square roots are used in algorithms for encryption, image processing, and game physics.
- Cryptography: Square roots play a role in cryptographic algorithms to ensure secure data transmission and authentication through digital signatures.
- Navigation: Square roots help calculate distances between points on a map or globe, aiding in navigation for pilots and mariners.
- Electrical Engineering: Electrical engineers use square roots to compute power, voltage, and current in circuits, crucial for designing efficient electrical systems.
- Cooking: When scaling recipes, square roots help maintain the correct balance of ingredients to ensure consistent flavor and texture.
- Photography: The aperture of a camera lens, expressed as an f-number, involves square roots to control the amount of light entering the camera.
- Accident Investigations: Police use square roots to determine the speed of vehicles based on skid marks in car accidents.
Common Mistakes and How to Avoid Them
When simplifying square roots, it's essential to be aware of common mistakes to ensure accuracy. Here are some frequent errors and tips on how to avoid them:
- Incorrect Factorization: Ensure the number inside the square root is correctly factored into its prime factors. For example, when simplifying \( \sqrt{36} \), remember that \( 36 = 6 \times 6 \).
- Misapplying the Product Property: One common mistake is incorrectly using the product property of square roots. The product property states that \( \sqrt{ab} = \sqrt{a} \cdot \sqrt{b} \). Ensure each factor is a perfect square when applying this property.
- Ignoring Negative Signs: Remember that the square root of a negative number is not a real number. If you encounter \( \sqrt{-36} \), recognize that this requires imaginary numbers, resulting in \( 6i \).
- Adding or Subtracting Square Roots Incorrectly: Another mistake is to incorrectly add or subtract square roots. For instance, \( \sqrt{a} + \sqrt{b} \) does not equal \( \sqrt{a + b} \). Simplify each square root separately.
- Overlooking Simplification: Ensure that the square root is fully simplified. For example, \( \sqrt{36} = 6 \) should be simplified completely, not left as \( \sqrt{36} \).
- Not Using the Quotient Property Correctly: The quotient property states that \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \). Ensure this property is used correctly when dealing with fractions.
By understanding and avoiding these common mistakes, you can ensure accurate and efficient simplification of square roots.
Additional Resources and Practice Problems
For further understanding and practice, here are some valuable resources and problems to help you master simplifying square roots:
-
Khan Academy: Offers comprehensive lessons and practice exercises on simplifying square roots. You can access the lessons .
-
Symbolab: Provides step-by-step solutions and explanations for various square root problems. Visit the site for more details.
-
Third Space Learning: Offers detailed guides and practice problems to enhance your skills in simplifying square roots. Check out their resources .
-
Varsity Tutors: Includes a variety of practice questions and detailed solutions on simplifying square roots. Find the practice problems .
Practice Problems
-
Simplify the following square roots:
- \(\sqrt{49}\)
- \(\sqrt{81}\)
- \(\sqrt{64}\)
-
Find the square root of the following expressions:
- \(\sqrt{16x^2}\)
- \(\sqrt{9y^4}\)
- \(\sqrt{25z^6}\)
-
Simplify the following radical expressions:
- \(\sqrt{50}\)
- \(\sqrt{72}\)
- \(\sqrt{98}\)
These resources and problems will provide you with a solid foundation in simplifying square roots, helping you to master this important mathematical concept.
Hướng dẫn cách đơn giản hóa căn bậc hai của 36 để thu hút người xem.
Cách Đơn Giản Hóa Căn Bậc Hai Của 36: sqrt(36)
READ MORE:
Hướng dẫn cách đơn giản hóa căn bậc hai của số nguyên, đặc biệt là căn(36), để thu hút người xem.
Cách Đơn Giản Hóa Căn Bậc Hai Của Số Nguyên, Căn(36)
















