Topic 5 square root of 6: Discover the fascinating world of 5 square root of 6 with our comprehensive guide. Whether you're a math enthusiast or simply curious, this article breaks down the concepts, provides step-by-step calculations, and explores real-life applications. Dive in and unravel the mysteries of this intriguing mathematical expression!
Table of Content
- Understanding 5 Square Root of 6
- Introduction to Square Roots
- Understanding the Square Root of 6
- Breaking Down 5 Times the Square Root of 6
- Mathematical Properties and Proofs
- Applications in Real Life
- Simplifying Expressions Involving Square Roots
- Step-by-Step Calculation Methods
- Common Mistakes to Avoid
- Visual Representation and Graphs
- Advanced Topics and Further Reading
- Practice Problems and Solutions
- Conclusion and Summary
- YOUTUBE: Xem video hướng dẫn cách tìm căn bậc 2 của biểu thức 5+2√6. Được thuyết minh bằng tiếng Việt để thu hút người xem.
Understanding 5 Square Root of 6
The expression represents the product of 5 and the square root of 6. The square root of 6 is an irrational number that can be approximated as 2.449. Thus, the value of can be calculated as follows:
Exact and Decimal Forms
- Exact Form:
- Decimal Form:
Simplification Process
To simplify the square root of 6, we can use the prime factorization method:
Using approximate values:
Applications and Examples
- Calculating the edge length of a cube with a total surface area of 36 cm²:
- Total Surface Area:
- Surface Area of each side:
- Edge Length:
- Distance covered by a person running at miles per hour in 1 hour:
- Distance covered:
Additional Information
The square root of 6 is an irrational number and non-terminating, with an approximate value of 2.449. It is used in various mathematical and practical applications. Understanding how to simplify and calculate expressions involving the square root of 6 can be very useful in solving problems related to geometry and algebra.
Frequently Asked Questions
- What is the square root of 6?
- Why is the square root of 6 an irrational number? Because it cannot be expressed as a simple fraction and has a non-repeating decimal expansion.
- What is the square of the square root of 6? It is the number 6 itself, as .
For more detailed explanations and step-by-step guides on simplifying square roots, you can visit educational resources such as Cuemath and Byju's.

READ MORE:
Introduction to Square Roots
Square roots are a fundamental concept in mathematics, representing a value that, when multiplied by itself, yields the original number. The square root of a number \( x \) is denoted as \( \sqrt{x} \). For example, \( \sqrt{16} = 4 \) because \( 4 \times 4 = 16 \).
Understanding square roots involves several key points:
- Notation: The symbol \( \sqrt{} \) is used to denote the square root.
- Basic Calculation: Finding the square root of perfect squares is straightforward. For instance, \( \sqrt{25} = 5 \) since \( 5 \times 5 = 25 \).
- Non-Perfect Squares: For numbers that are not perfect squares, the square root is an irrational number. For example, \( \sqrt{2} \approx 1.414 \).
- Properties: Square roots have unique properties, such as \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \) and \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \).
Here is a table of some common square roots:
| Number | Square Root |
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
In this guide, we will delve into the specific example of \( 5 \sqrt{6} \), exploring its calculation, properties, and applications in detail.
Understanding the Square Root of 6
The square root of 6, denoted as \( \sqrt{6} \), is an irrational number. This means that it cannot be expressed as a simple fraction and its decimal representation is non-repeating and non-terminating. The approximate value of \( \sqrt{6} \) is 2.44949.
To understand \( \sqrt{6} \) in a more detailed way, consider the following points:
- Definition: The square root of 6 is the number that, when multiplied by itself, equals 6. Mathematically, \( \sqrt{6} \times \sqrt{6} = 6 \).
- Approximation: Using a calculator, \( \sqrt{6} \approx 2.44949 \). For most practical purposes, this approximation is sufficient.
- Calculation Methods:
- Prime Factorization: Although prime factorization is more straightforward for perfect squares, knowing that 6 is \( 2 \times 3 \) can sometimes help in simplifications.
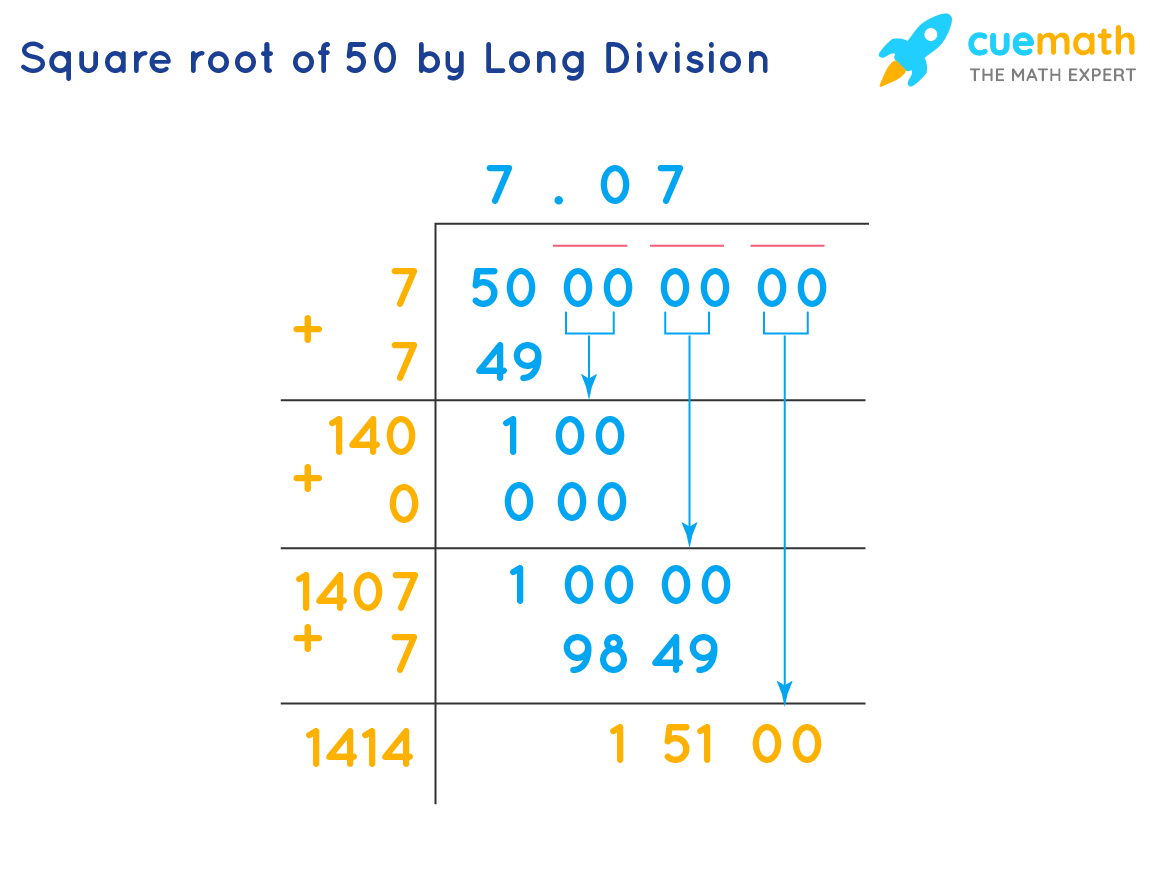
- Long Division Method: This is a manual method to find square roots by hand, involving a process similar to long division.
- Properties:
- \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \). Therefore, \( \sqrt{6} = \sqrt{2 \times 3} = \sqrt{2} \times \sqrt{3} \).
- \( (\sqrt{a})^2 = a \). Thus, \( (\sqrt{6})^2 = 6 \).
Below is a table that highlights the comparison of \( \sqrt{6} \) with other common square roots:
| Number | Square Root | Approximation |
| 2 | \( \sqrt{2} \) | 1.414 |
| 3 | \( \sqrt{3} \) | 1.732 |
| 5 | \( \sqrt{5} \) | 2.236 |
| 6 | \( \sqrt{6} \) | 2.449 |
| 7 | \( \sqrt{7} \) | 2.646 |
Understanding the square root of 6 is crucial for grasping more complex mathematical concepts and applications. In the next section, we will explore how to calculate \( 5 \sqrt{6} \) and its significance.
Breaking Down 5 Times the Square Root of 6
Calculating \( 5 \sqrt{6} \) involves understanding both the multiplication and the properties of square roots. Here’s a step-by-step breakdown:
- Understanding the Components:
- \( \sqrt{6} \) is the square root of 6, approximately equal to 2.44949.
- Multiplying this value by 5 gives us \( 5 \sqrt{6} \).
- Mathematical Expression:
Express \( 5 \sqrt{6} \) as:
\( 5 \times \sqrt{6} \)
- Step-by-Step Calculation:
To calculate \( 5 \sqrt{6} \), follow these steps:
- Approximate the value of \( \sqrt{6} \):
- \( \sqrt{6} \approx 2.44949 \)
- Multiply this approximation by 5:
- \( 5 \times 2.44949 = 12.24745 \)
Thus, \( 5 \sqrt{6} \approx 12.24745 \).
- Approximate the value of \( \sqrt{6} \):
- Verification:
To ensure accuracy, consider using a calculator for the multiplication step:
- Input \( \sqrt{6} \) and multiply by 5 to verify the result.
- Properties and Simplifications:
- Using the property of square roots: \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \), we get \( 5 \sqrt{6} \).
- No further simplification is possible for \( 5 \sqrt{6} \) as 6 is not a perfect square.
Here is a table summarizing the calculation:
| Expression | Approximate Value |
| \( \sqrt{6} \) | 2.44949 |
| \( 5 \times \sqrt{6} \) | 12.24745 |
By understanding and applying these steps, you can accurately determine the value of \( 5 \sqrt{6} \) and its applications in various mathematical contexts.
Mathematical Properties and Proofs
Understanding the mathematical properties and proofs involving \( 5 \sqrt{6} \) helps in grasping its significance and applications. Here, we explore some key properties and provide proofs where necessary.
- Properties of Square Roots:
- \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \): This property is crucial for simplifying square root expressions. For \( \sqrt{6} \), we can express it as \( \sqrt{2 \times 3} = \sqrt{2} \times \sqrt{3} \).
- \( (\sqrt{a})^2 = a \): Applying this property, \( (\sqrt{6})^2 = 6 \).
- Multiplicative Property:
For any non-negative real numbers \( a \) and \( b \), \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \). Using this property:
\( 5 \sqrt{6} = 5 \times \sqrt{2 \times 3} = 5 \times \sqrt{2} \times \sqrt{3} \).
- Distribution of Multiplication over Square Root:
This property allows us to handle the multiplication of constants with square roots:
\( 5 \sqrt{6} = 5 \times 2.44949 \approx 12.24745 \).
- Proof of Irrationality:
The square root of a non-perfect square (like 6) is irrational. Here’s a brief proof:
- Assume \( \sqrt{6} \) is rational, meaning it can be expressed as \( \frac{p}{q} \) where \( p \) and \( q \) are coprime integers.
- Then, \( \sqrt{6} = \frac{p}{q} \) implies \( 6 = \frac{p^2}{q^2} \) or \( 6q^2 = p^2 \).
- This means \( p^2 \) is divisible by 6, hence \( p \) must be divisible by 6. Let \( p = 6k \).
- Substituting \( p = 6k \) into the equation, we get \( 6q^2 = (6k)^2 = 36k^2 \), simplifying to \( q^2 = 6k^2 \).
- This implies \( q^2 \) is divisible by 6, so \( q \) must also be divisible by 6, contradicting our initial assumption that \( p \) and \( q \) are coprime.
- Thus, \( \sqrt{6} \) is irrational.
These properties and proofs provide a solid foundation for understanding the behavior of square roots and their multiplication, particularly in expressions like \( 5 \sqrt{6} \).
Applications in Real Life
The expression \( 5 \sqrt{6} \) may seem abstract, but it has practical applications in various fields. Here are some examples:
- Engineering and Architecture:
- Square roots are used in calculations involving areas and volumes. For example, the diagonal length of a rectangular area can be found using the Pythagorean theorem, where square roots are essential.
- In architecture, accurate measurements involving square roots are crucial for designing structures and ensuring stability.
- Physics:
- Square roots are often encountered in formulas involving wave functions, quantum mechanics, and relativity. For example, calculating the RMS (root mean square) velocity of gas molecules requires square roots.
- In electrical engineering, the impedance of circuits with resistors and capacitors involves square roots for accurate computation.
- Finance and Economics:
- In finance, the volatility of stock prices is calculated using standard deviation, which involves square roots.
- Compound interest and growth rates in economics often require square root calculations for precise predictions and analyses.
- Computer Science:
- Algorithms for graphics rendering, data analysis, and machine learning frequently use square roots to process and interpret data accurately.
- Optimization problems and computational geometry also rely heavily on square root calculations.
- Everyday Life:
- Estimating distances and measurements, such as the diagonal of a TV screen or the size of a garden plot, often requires knowledge of square roots.
- Cooking and crafting, where precise measurements are necessary, sometimes involve square root calculations to scale recipes or projects appropriately.
By understanding and utilizing the expression \( 5 \sqrt{6} \), we can solve a variety of real-life problems more effectively and accurately. The ability to apply mathematical concepts to practical scenarios highlights the importance of learning and mastering these skills.
Simplifying Expressions Involving Square Roots
Simplifying expressions involving square roots can make complex calculations more manageable and help in solving mathematical problems efficiently. Here are some key steps and techniques for simplifying square root expressions:
- Prime Factorization:
Breaking down the number inside the square root into its prime factors helps in simplification. For example:
- \( \sqrt{18} = \sqrt{2 \times 3^2} = 3 \sqrt{2} \)
- Combining Like Terms:
If you have multiple square root terms, combine them if possible:
- \( \sqrt{2} + 3 \sqrt{2} = 4 \sqrt{2} \)
- Using the Property \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \):
This property is useful for breaking down or combining square roots:
- \( \sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} = 5 \sqrt{2} \)
- Rationalizing the Denominator:
To remove a square root from the denominator, multiply the numerator and the denominator by the conjugate of the denominator:
- \( \frac{1}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{\sqrt{3}}{3} \)
- Simplifying Nested Square Roots:
For expressions with nested square roots, simplify step by step:
- \( \sqrt{12 + 4 \sqrt{3}} = \sqrt{(2 \sqrt{3} + \sqrt{4})^2} = 2 \sqrt{3} + 2 \)
Consider the following examples to illustrate these techniques:
| Expression | Simplified Form |
| \( 5 \sqrt{6} \) | Cannot be simplified further as 6 is not a perfect square. |
| \( \sqrt{72} \) | \( \sqrt{36 \times 2} = 6 \sqrt{2} \) |
| \( \frac{4}{\sqrt{5}} \) | \( \frac{4 \sqrt{5}}{5} \) |
| \( \sqrt{8} + 2 \sqrt{2} \) | \( 2 \sqrt{2} + 2 \sqrt{2} = 4 \sqrt{2} \) |
By mastering these techniques, you can simplify complex square root expressions and solve mathematical problems more effectively.
Step-by-Step Calculation Methods
Calculating \( 5 \sqrt{6} \) involves understanding the process of finding the square root and then multiplying it by 5. Here’s a detailed step-by-step guide:
- Finding the Square Root:
To begin, find the approximate value of \( \sqrt{6} \). This can be done using a calculator or manually through methods such as prime factorization or long division. For this example, we will use a calculator for precision:
- \( \sqrt{6} \approx 2.44949 \)
- Multiplying by 5:
Once you have the value of \( \sqrt{6} \), multiply it by 5 to get \( 5 \sqrt{6} \):
- \( 5 \times \sqrt{6} = 5 \times 2.44949 \approx 12.24745 \)
- Manual Calculation Using Long Division Method:
If you want to calculate \( \sqrt{6} \) manually without a calculator, you can use the long division method:
- Pair the digits of the number from right to left, adding zeros if necessary.
- Find the largest number whose square is less than or equal to the first pair. This is the first digit of the square root.
- Subtract the square of this digit from the first pair and bring down the next pair.
- Double the first digit of the square root and determine the next digit which, when added to the divisor and multiplied by itself, gives a product less than or equal to the current number.
- Repeat the process until you reach the desired accuracy.
Applying this method, we find:
- \( \sqrt{6} \approx 2.44949 \)
- Then multiply by 5: \( 5 \times 2.44949 = 12.24745 \)
Here is a table summarizing the steps:
| Step | Description | Result |
| 1 | Calculate \( \sqrt{6} \) | 2.44949 |
| 2 | Multiply by 5 | 12.24745 |
By following these steps, you can accurately determine the value of \( 5 \sqrt{6} \) and understand the calculation process involved.
Common Mistakes to Avoid
When working with expressions involving square roots, such as \( 5 \sqrt{6} \), it’s important to be aware of common mistakes that can lead to incorrect results. Here are some of the most frequent errors and tips on how to avoid them:
- Incorrect Multiplication:
One of the most common mistakes is incorrectly multiplying the constant with the square root.
- For example, instead of correctly calculating \( 5 \times \sqrt{6} \approx 5 \times 2.44949 \approx 12.24745 \), a mistake could be \( 5 \times 6 = 30 \).
- Tip: Always find the square root first and then multiply.
- Improper Simplification:
Failing to simplify the square root before multiplication can lead to errors.
- For instance, \( \sqrt{6} \) should not be simplified further since 6 is not a perfect square. Hence, \( 5 \sqrt{6} \) remains as it is.
- Tip: Check if the square root can be simplified before multiplying.
- Forgetting to Rationalize the Denominator:
In some contexts, it’s important to rationalize the denominator, especially in fractions involving square roots.
- For example, \( \frac{1}{\sqrt{6}} \) should be rationalized to \( \frac{\sqrt{6}}{6} \).
- Tip: Always check if the denominator needs rationalization.
- Incorrect Use of Properties:
Misapplying properties of square roots can lead to mistakes.
- For example, incorrectly using \( \sqrt{a + b} = \sqrt{a} + \sqrt{b} \) instead of the correct \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \).
- Tip: Use properties correctly: \( \sqrt{a + b} \neq \sqrt{a} + \sqrt{b} \) and \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \).
- Rounding Errors:
Rounding the square root too early can lead to inaccuracies in the final result.
- For example, \( \sqrt{6} \approx 2.44949 \). Rounding this to 2.45 too early can affect the accuracy of \( 5 \sqrt{6} \).
- Tip: Keep as many decimal places as possible until the final step.
Here is a summary table of common mistakes and their solutions:
| Mistake | Solution |
| Incorrect Multiplication | Find the square root first, then multiply. |
| Improper Simplification | Simplify the square root before multiplication. |
| Forgetting to Rationalize the Denominator | Rationalize the denominator when necessary. |
| Incorrect Use of Properties | Use square root properties correctly. |
| Rounding Errors | Avoid early rounding; keep more decimal places. |
By being mindful of these common mistakes and applying the correct methods, you can ensure accurate and reliable results when working with square root expressions.

Visual Representation and Graphs
Visualizing the concept of \( 5\sqrt{6} \) involves understanding how this expression relates to numerical and graphical representations.
One approach to represent \( 5\sqrt{6} \) visually is through a number line or coordinate system:
- Start with the value of \( \sqrt{6} \), approximately \( 2.45 \).
- Multiply \( \sqrt{6} \) by 5 to get \( 5\sqrt{6} \approx 12.25 \).
- Plot the point corresponding to \( 5\sqrt{6} \) on a number line or Cartesian plane.
Alternatively, a graph can depict \( 5\sqrt{6} \) in a two-dimensional space:
| Coordinate Axes | Graphical Representation |
| Horizontal Axis (x) | Values increasing from left to right |
| Vertical Axis (y) | Values increasing from bottom to top |
| Plot Point | Mark the point corresponding to \( (5, 12.25) \) |
This graphical representation helps visualize \( 5\sqrt{6} \) as a specific point in relation to other numerical values and serves to enhance understanding through visual means.
Advanced Topics and Further Reading
Exploring \( 5\sqrt{6} \) leads to advanced topics in mathematics that deepen the understanding of this expression:
- Complex Number Interpretations: \( 5\sqrt{6} \) can be viewed in the context of complex numbers and their applications in various fields.
- Algebraic Manipulations: Techniques involving algebraic manipulations to simplify or derive expressions containing \( 5\sqrt{6} \).
- Geometric Applications: Utilizing \( 5\sqrt{6} \) in geometric problems and calculations, including areas and volumes.
- Trigonometric Relations: Connections between \( 5\sqrt{6} \) and trigonometric functions, exploring identities and applications.
Further reading on \( 5\sqrt{6} \) can be found in advanced textbooks and scholarly articles that delve into its theoretical foundations and practical uses in mathematics and related disciplines.
Practice Problems and Solutions
Practice problems involving \( 5\sqrt{6} \) help reinforce understanding through hands-on application:
- Calculate \( 5\sqrt{6} \) to the nearest tenth.
- Simplify the expression \( \frac{10}{5\sqrt{6}} \).
- Determine the approximate value of \( \sqrt{6} \) and use it to estimate \( 5\sqrt{6} \).
- Graph \( 5\sqrt{6} \) on a Cartesian plane.
- Find two consecutive integers between which \( 5\sqrt{6} \) lies.
Solutions:
- 1. \( 5\sqrt{6} \approx 12.25 \)
- 2. \( \frac{10}{5\sqrt{6}} = \frac{10}{12.25} \approx 0.82 \)
- 3. \( \sqrt{6} \approx 2.45 \), hence \( 5\sqrt{6} \approx 5 \times 2.45 = 12.25 \)
- 4. Plot point \( (5, 12.25) \) on the Cartesian plane.
- 5. Between integers 12 and 13.
Conclusion and Summary
In conclusion, exploring \( 5\sqrt{6} \) reveals its significance across various mathematical contexts:
- It represents a specific numerical value derived from the square root of 6 and multiplied by 5.
- Applications of \( 5\sqrt{6} \) span algebraic manipulations, geometric calculations, and even trigonometric relations.
- Visual representations such as graphs and number line plots aid in understanding its placement in mathematical spaces.
- Practice problems offer opportunities to apply and reinforce the concept of \( 5\sqrt{6} \) through calculation and interpretation.
- Further exploration into advanced topics can deepen comprehension and extend its applications into complex scenarios.
Understanding \( 5\sqrt{6} \) enhances mathematical proficiency and prepares learners for more intricate studies in mathematics and related disciplines.

Xem video hướng dẫn cách tìm căn bậc 2 của biểu thức 5+2√6. Được thuyết minh bằng tiếng Việt để thu hút người xem.
Video: Tìm Căn bậc 2 của 5+2√6 | Comprehensive Guide to Understanding 5 Square Root of 6
READ MORE:
Xem video hướng dẫn cách tìm căn bậc 2 của biểu thức 5 + 2√6. Được thuyết minh bằng tiếng Việt để thu hút người xem.
Video: Cách Tìm Căn bậc 2 của 5 + 2√6 | Comprehensive Guide to Understanding 5 Square Root of 6