Topic square root of 5 + square root of 5: Discover how to simplify the expression square root of 5 + square root of 5 in this easy-to-understand guide. Learn the basic principles of square roots, see step-by-step calculations, and explore real-world applications of this fundamental mathematical concept.
Table of Content
- Square Root Calculation
- Introduction to Square Roots
- Basic Calculation of Square Root of 5 + Square Root of 5
- Mathematical Properties of Square Roots
- Simplifying Square Root Expressions
- Real-World Applications of Square Roots
- Graphical Representation of Square Roots
- Common Mistakes in Calculating Square Roots
- Advanced Square Root Calculations
- Historical Context of Square Roots
- Frequently Asked Questions About Square Roots
- YOUTUBE:
Square Root Calculation
The expression \(\sqrt{5} + \sqrt{5}\) is a simple mathematical addition involving square roots.
Calculation
To add two square roots of the same number, you can factor out the common square root:
\[
\sqrt{5} + \sqrt{5} = 2\sqrt{5}
\]
Understanding the Result
Here, the number 2 is the coefficient and \(\sqrt{5}\) remains as it is. The result is a simplified form of the addition of square roots.
Applications
- Mathematical problems involving roots
- Algebraic simplification
- Geometry involving irrational numbers
Related Visuals
Graphs and visual representations often help in understanding the behavior of square roots. Below is an example of a graph showing y = \sqrt{5} and y = 2\sqrt{5}.

Examples in Context
Consider a right triangle where the lengths of the legs are both \(\sqrt{5}\). The hypotenuse \(c\) can be calculated using the Pythagorean theorem:
\[
c = \sqrt{(\sqrt{5})^2 + (\sqrt{5})^2} = \sqrt{5 + 5} = \sqrt{10}
\]
| Expression | Result |
|---|---|
| \(\sqrt{5} + \sqrt{5}\) | \(2\sqrt{5}\) |
| \(\sqrt{5} \cdot \sqrt{5}\) | 5 |
Further Reading
- Properties of Square Roots
- Applications of Irrational Numbers
- Understanding Algebraic Expressions

READ MORE:
Introduction to Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. It is a fundamental concept in mathematics, often represented by the radical symbol √. For example, the square root of 25 is 5, since \(5 \times 5 = 25\).
Let's break down the basics of square roots step by step:
- Definition: The square root of a number \( x \) is a number \( y \) such that \( y^2 = x \). It is denoted as \( \sqrt{x} \).
- Positive and Negative Roots: Every positive number has two square roots: one positive and one negative. For example, the square roots of 16 are 4 and -4 because \( 4^2 = 16 \) and \( (-4)^2 = 16 \).
- Principal Square Root: The non-negative square root is called the principal square root. When we refer to \( \sqrt{x} \), we usually mean the principal square root.
- Irrational Numbers: Some square roots, like \( \sqrt{5} \), are irrational numbers. They cannot be expressed as a simple fraction and have non-repeating, non-terminating decimal expansions.
Consider the expression \( \sqrt{5} + \sqrt{5} \):
Since both terms are the same, we can factor out the common square root:
\[
\sqrt{5} + \sqrt{5} = 2\sqrt{5}
\]
This is a simplified form of the addition of square roots.
Understanding square roots is crucial for various applications in mathematics, including solving quadratic equations, working with geometric shapes, and analyzing scientific data.
- Solving equations: Square roots are used to solve quadratic equations, where the solution involves finding the roots of a polynomial.
- Geometry: Square roots help in calculating the lengths of sides in right triangles using the Pythagorean theorem.
- Science: Square roots are used in physics and engineering to analyze waveforms, signal processing, and other phenomena.
Basic Calculation of Square Root of 5 + Square Root of 5
Calculating the sum of two identical square roots is straightforward. Here, we will calculate \( \sqrt{5} + \sqrt{5} \) step by step:
- Identify the Terms: Recognize that both terms under the radical are identical. In this case, both are \( \sqrt{5} \).
- Factor Out the Common Square Root: Since both terms are \( \sqrt{5} \), we can factor out the common square root:
\[
\sqrt{5} + \sqrt{5}
\] - Simplify the Expression: Combine the terms by adding the coefficients:
\[
\sqrt{5} + \sqrt{5} = 2 \times \sqrt{5} = 2\sqrt{5}
\]
Thus, the simplified form of \( \sqrt{5} + \sqrt{5} \) is \( 2\sqrt{5} \).
To understand this better, consider the properties of square roots and coefficients:
- Square Roots as Factors: When adding square roots, treat them as like terms if the radicands (the numbers inside the square root) are the same.
- Coefficients: The number outside the square root symbol acts as a coefficient, similar to how coefficients work in algebra.
Here is a tabular representation of the calculation:
| Expression | Step | Result |
|---|---|---|
| \(\sqrt{5} + \sqrt{5}\) | Identify like terms | \(\sqrt{5} + \sqrt{5}\) |
| \(\sqrt{5} + \sqrt{5}\) | Factor out the common square root | \(2 \times \sqrt{5}\) |
| \(2 \times \sqrt{5}\) | Simplify | \(2\sqrt{5}\) |
This simplified form, \( 2\sqrt{5} \), is useful in various mathematical contexts, including algebra, geometry, and more advanced mathematical fields.
Mathematical Properties of Square Roots
Square roots possess several important mathematical properties that make them fundamental in various calculations. Here, we explore these properties in detail:
- Non-negative Principle: The principal square root of a non-negative number is always non-negative.
\[
\sqrt{x} \geq 0 \quad \text{for all} \quad x \geq 0
\] - Product Property: The square root of a product is equal to the product of the square roots of the factors.
\[
\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}
\]For example,
\[
\sqrt{4 \cdot 9} = \sqrt{36} = 6 \quad \text{and} \quad \sqrt{4} \cdot \sqrt{9} = 2 \cdot 3 = 6
\] - Quotient Property: The square root of a quotient is equal to the quotient of the square roots of the numerator and denominator.
\[
\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}
\]For example,
\[
\sqrt{\frac{25}{9}} = \frac{\sqrt{25}}{\sqrt{9}} = \frac{5}{3}
\] - Sum and Difference: The square root of a sum or difference cannot be simplified into the sum or difference of the square roots of the individual terms.
\[
\sqrt{a + b} \neq \sqrt{a} + \sqrt{b} \quad \text{and} \quad \sqrt{a - b} \neq \sqrt{a} - \sqrt{b}
\] - Power Property: The square root of a number raised to a power can be expressed as the number raised to half that power.
\[
\sqrt{a^2} = a \quad \text{and} \quad \sqrt{a^4} = a^2
\] - Irrational Numbers: The square root of a non-perfect square is an irrational number. Irrational numbers cannot be expressed as a simple fraction and have non-repeating, non-terminating decimal expansions.
For example,
\[
\sqrt{5} \approx 2.23606797749979
\]
These properties are essential in simplifying and solving various mathematical problems. Let's see these properties in action with the expression \( \sqrt{5} + \sqrt{5} \):
- Applying the Sum Property: Since both terms are identical, we combine them as follows:
\[
\sqrt{5} + \sqrt{5} = 2\sqrt{5}
\] - Simplification: This shows that the sum of two identical square roots is just twice the value of one of them.
| Property | Example | Result |
|---|---|---|
| Product Property | \(\sqrt{4 \cdot 9}\) | \(6\) |
| Quotient Property | \(\sqrt{\frac{25}{9}}\) | \(\frac{5}{3}\) |
| Power Property | \(\sqrt{a^4}\) | \(a^2\) |
Understanding these properties allows for more efficient problem-solving and a deeper comprehension of mathematical relationships.
Simplifying Square Root Expressions
Simplifying square root expressions involves combining like terms, rationalizing denominators, and using algebraic properties to make expressions more manageable. Here, we will explore these techniques step by step.
- Combining Like Terms: When dealing with square roots of the same number, you can combine them as you would like terms in algebra.
For example, to simplify \( \sqrt{5} + \sqrt{5} \):
\[
\sqrt{5} + \sqrt{5} = 2\sqrt{5}
\] - Rationalizing the Denominator: To eliminate square roots from the denominator, multiply both the numerator and denominator by the conjugate of the denominator.
For example, to simplify \(\frac{1}{\sqrt{5}}\):
\[
\frac{1}{\sqrt{5}} \times \frac{\sqrt{5}}{\sqrt{5}} = \frac{\sqrt{5}}{5}
\] - Using the Distributive Property: When a square root expression is multiplied by a sum or difference, apply the distributive property.
For example, to simplify \( \sqrt{5}(2 + \sqrt{3}) \):
\[
\sqrt{5}(2 + \sqrt{3}) = 2\sqrt{5} + \sqrt{15}
\] - Squaring to Eliminate Square Roots: In some cases, squaring both sides of an equation can help eliminate square roots.
For example, to solve \( \sqrt{x} = 3 \):
\[
(\sqrt{x})^2 = 3^2 \implies x = 9
\]
Below is a table summarizing key techniques for simplifying square root expressions:
| Technique | Example | Result |
|---|---|---|
| Combining Like Terms | \(\sqrt{5} + \sqrt{5}\) | \(2\sqrt{5}\) |
| Rationalizing the Denominator | \(\frac{1}{\sqrt{5}}\) | \(\frac{\sqrt{5}}{5}\) |
| Distributive Property | \(\sqrt{5}(2 + \sqrt{3})\) | \(2\sqrt{5} + \sqrt{15}\) |
| Squaring | \(\sqrt{x} = 3\) | \(x = 9\) |
By mastering these techniques, you can simplify complex square root expressions and solve a wide range of mathematical problems efficiently.

Real-World Applications of Square Roots
Square roots are fundamental in various real-world applications, spanning multiple fields such as science, engineering, finance, and everyday problem-solving. Below, we explore some of the key applications of square roots.
- Geometry and Trigonometry:
Square roots are crucial in calculating distances, areas, and angles in geometric shapes.
- Pythagorean Theorem: In a right triangle, the length of the hypotenuse is found using the square root of the sum of the squares of the other two sides.
\[
c = \sqrt{a^2 + b^2}
\] - Circle Measurements: The radius of a circle can be determined from the area using the square root.
\[
r = \sqrt{\frac{A}{\pi}}
\]
- Pythagorean Theorem: In a right triangle, the length of the hypotenuse is found using the square root of the sum of the squares of the other two sides.
- Physics:
Square roots are used in formulas to describe natural phenomena.
- Motion Equations: The magnitude of velocity and acceleration in uniform circular motion often involves square roots.
- Wave Speed: The speed of a wave on a string is given by the square root of the tension divided by the linear mass density.
\[
v = \sqrt{\frac{T}{\mu}}
\]
- Engineering:
Square roots are vital in structural analysis, electrical engineering, and material science.
- Stress and Strain Calculations: The square root helps determine material properties under load.
- Electrical Circuits: The root mean square (RMS) value of alternating current is calculated using the square root of the average of the squares of the instantaneous values.
- Finance:
Square roots are applied in risk assessment, loan calculations, and investment models.
- Standard Deviation: In statistics, the square root of the variance gives the standard deviation, a measure of risk or volatility in finance.
\[
\sigma = \sqrt{\frac{\sum (x_i - \mu)^2}{N}}
\] - Compound Interest: The formula for compound interest sometimes involves square roots, especially in continuous compounding scenarios.
- Standard Deviation: In statistics, the square root of the variance gives the standard deviation, a measure of risk or volatility in finance.
- Everyday Problem-Solving:
Square roots are often used in daily tasks such as cooking, construction, and navigation.
- Cooking: Adjusting recipes proportionally may require the use of square roots.
- Construction: Calculating the diagonal of a rectangular space or determining the correct length of materials.
- Navigation: Determining the shortest path between two points can involve square roots, especially in diagonal measurements.
Understanding and applying square roots enables us to solve a variety of practical problems efficiently and accurately.
Graphical Representation of Square Roots
Graphing square roots helps in visualizing their behavior and understanding their properties. Here, we will explore how to graph square root functions and interpret their characteristics step by step.
- Basic Square Root Function:
The basic square root function is \( y = \sqrt{x} \). This function is defined for all non-negative values of \( x \) and represents the positive square root of \( x \).
- The graph of \( y = \sqrt{x} \) starts at the origin (0,0) and increases gradually, forming a curve.
- The domain of the function is \( x \geq 0 \), and the range is \( y \geq 0 \).
Graphically, it looks like this:
\[
\text{Insert a graph of } y = \sqrt{x} \text{ here.}
\] - Transformations of the Square Root Function:
Transformations include translations, reflections, and scaling. These can be applied to the basic function to shift or stretch the graph.
- Horizontal Shift: \( y = \sqrt{x - h} \)
This shifts the graph \( h \) units to the right if \( h \) is positive, or \( h \) units to the left if \( h \) is negative.
- Vertical Shift: \( y = \sqrt{x} + k \)
This shifts the graph \( k \) units up if \( k \) is positive, or \( k \) units down if \( k \) is negative.
- Reflection: \( y = -\sqrt{x} \)
This reflects the graph across the x-axis.
- Vertical Stretch/Compression: \( y = a\sqrt{x} \)
If \( a > 1 \), the graph is stretched vertically. If \( 0 < a < 1 \), the graph is compressed vertically.
- Horizontal Shift: \( y = \sqrt{x - h} \)
- Example:
Consider the function \( y = 2\sqrt{x - 3} + 1 \). Let's break down the transformations step by step:
- Horizontal Shift: \( \sqrt{x - 3} \)
This shifts the graph 3 units to the right.
- Vertical Stretch: \( 2\sqrt{x - 3} \)
This stretches the graph vertically by a factor of 2.
- Vertical Shift: \( 2\sqrt{x - 3} + 1 \)
This shifts the graph 1 unit up.
Graphically, it looks like this:
\[
\text{Insert a graph of } y = 2\sqrt{x - 3} + 1 \text{ here.}
\] - Horizontal Shift: \( \sqrt{x - 3} \)
Below is a table summarizing the transformations of the square root function:
| Transformation | Equation | Effect on Graph |
|---|---|---|
| Horizontal Shift | \( y = \sqrt{x - h} \) | Shifts right if \( h > 0 \), left if \( h < 0 \) |
| Vertical Shift | \( y = \sqrt{x} + k \) | Shifts up if \( k > 0 \), down if \( k < 0 \) |
| Reflection | \( y = -\sqrt{x} \) | Reflects across the x-axis |
| Vertical Stretch/Compression | \( y = a\sqrt{x} \) | Stretches if \( a > 1 \), compresses if \( 0 < a < 1 \) |
Understanding these transformations allows for accurate graphing and interpretation of square root functions, which are essential in various mathematical and real-world applications.
Common Mistakes in Calculating Square Roots
Calculating square roots can sometimes be tricky, and there are several common mistakes that learners often make. Here are some of the most frequent errors and how to avoid them:
- Incorrect Simplification: One of the most common mistakes is incorrectly simplifying square root expressions. For example, assuming that \(\sqrt{a + b} = \sqrt{a} + \sqrt{b}\). This is incorrect as the square root of a sum is not the sum of the square roots.
- Misinterpreting Multiplication: Another frequent error is misunderstanding the product of square roots. The correct property is \(\sqrt{a} \times \sqrt{b} = \sqrt{a \times b}\), not \(\sqrt{a} \times \sqrt{b} = \sqrt{a + b}\).
- Incorrect Square Root Values: It's important to remember the approximate values of common square roots. For instance, \(\sqrt{5} \approx 2.236\). Using incorrect values can lead to significant errors in calculations.
- Neglecting Square Root Rules: Always remember the fundamental rules of square roots, such as \(\sqrt{a^2} = a\) and that square roots of negative numbers result in imaginary numbers (\(\sqrt{-1} = i\)).
- Arithmetic Mistakes: Basic arithmetic errors can also lead to incorrect results. Double-check your addition, subtraction, multiplication, and division when dealing with square roots.
By understanding these common pitfalls and practicing careful calculation, you can improve your accuracy and confidence in working with square roots.
Here's a table summarizing the common mistakes and correct approaches:
| Common Mistake | Incorrect Approach | Correct Approach |
|---|---|---|
| Incorrect Simplification | \(\sqrt{a + b} = \sqrt{a} + \sqrt{b}\) | \(\sqrt{a + b} \neq \sqrt{a} + \sqrt{b}\) |
| Misinterpreting Multiplication | \(\sqrt{a} \times \sqrt{b} = \sqrt{a + b}\) | \(\sqrt{a} \times \sqrt{b} = \sqrt{a \times b}\) |
| Incorrect Square Root Values | \(\sqrt{5} \approx 2.5\) | \(\sqrt{5} \approx 2.236\) |
| Neglecting Square Root Rules | \(\sqrt{-1} = \text{undefined}\) | \(\sqrt{-1} = i\) |
| Arithmetic Mistakes | Errors in basic operations | Double-check calculations |
Advanced Square Root Calculations
In this section, we explore more advanced concepts and methods for calculating square roots, specifically focusing on the expression √5 + √5. Understanding these methods can enhance your mathematical proficiency and provide deeper insights into the properties of square roots.
Properties of √5 + √5
To begin, let's recall that the expression √5 + √5 can be simplified using basic algebraic principles:
Advanced Simplification Techniques
Advanced simplification techniques often involve recognizing patterns or using algebraic identities. Here are a few methods:
- Using Algebraic Identities: The expression \( \sqrt{a} + \sqrt{a} \) can always be simplified to \( 2\sqrt{a} \). Applying this to our expression, we get \( 2\sqrt{5} \).
- Geometric Interpretation: The square root of a number can often be interpreted geometrically. For instance, \( \sqrt{5} \) is the length of the diagonal of a rectangle with sides 1 and 2 units.
Rational and Irrational Numbers
Understanding whether the results are rational or irrational is crucial. Since 5 is not a perfect square, \( \sqrt{5} \) is irrational. Thus, \( 2\sqrt{5} \) is also irrational.
Using advanced techniques, one can determine the properties and characteristics of such numbers:
This number continues infinitely without repeating, confirming its irrational nature.
Numerical Methods for Approximating Square Roots
When exact calculations are impractical, numerical methods can provide approximate values for square roots. Here are a few common methods:
- Babylonian Method: Also known as Heron's method, it iteratively improves guesses to get closer to the actual square root.
- Newton's Method: An extension of the Babylonian method, this approach uses calculus to refine guesses and achieve faster convergence.
Example: Calculating √5 + √5 Using Babylonian Method
- Initial Guess: Start with an initial guess, \( x_0 \), say 2.
- Iteration Formula: Use the formula
\( x_{n+1} = \frac{1}{2} \left( x_n + \frac{5}{x_n} \right) \) - Convergence: Repeat the iteration until the result converges to a stable value.
This method quickly converges to \( \sqrt{5} \approx 2.236 \), and thus, \( 2\sqrt{5} \approx 4.472 \).
Graphical Representation of √5
Visualizing square roots can aid in understanding. The number line and coordinate plane are useful tools:
- Number Line: Placing \( \sqrt{5} \) on a number line helps in comparing it with other numbers.
- Coordinate Plane: Plotting \( y = \sqrt{x} \) provides insights into the growth rate and behavior of the square root function.
Applications in Advanced Mathematics
Square roots, especially those of irrational numbers, have applications in various fields such as geometry, algebra, and calculus. For instance, they are essential in solving quadratic equations, analyzing functions, and understanding fractals and complex numbers.
Conclusion
Mastering advanced square root calculations, such as \( \sqrt{5} + \sqrt{5} \), involves understanding both the mathematical properties and the methods for approximation. These skills are invaluable for higher-level mathematics and practical problem-solving.
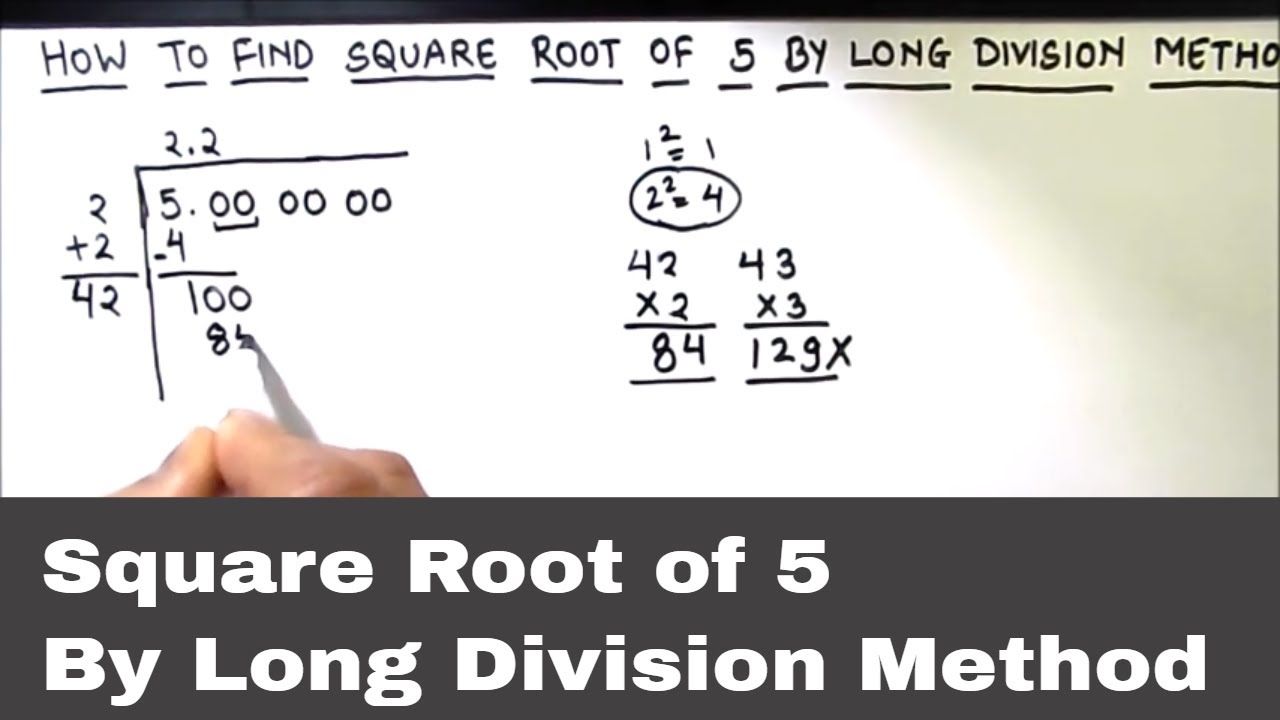
Historical Context of Square Roots
The concept of square roots has a rich history, with contributions from various ancient civilizations. Understanding the historical development of square roots not only highlights the evolution of mathematical thought but also reveals the diverse approaches and innovations made over centuries.
Ancient Civilizations
- Babylonian Mathematics: The Babylonians, around 2000 BCE, had methods to approximate square roots. They used a form of iterative approximation, much like the methods we use today, demonstrating their advanced understanding of mathematics.
- Egyptian Mathematics: The ancient Egyptians, as recorded in the Rhind Mathematical Papyrus (circa 1650 BCE), had practical methods for calculating square roots, primarily for architectural and surveying purposes.
- Chinese Mathematics: Ancient Chinese mathematicians developed methods for extracting square roots, as seen in the "Nine Chapters on the Mathematical Art" (circa 100 CE). They used a technique similar to long division, emphasizing the systematic approach to finding roots.
Greek Contributions
Greek mathematicians like Euclid (circa 300 BCE) provided a geometric interpretation of square roots. In "Elements," Euclid described methods to find the square root of a number using geometric means, laying the groundwork for future algebraic methods.
Medieval Islamic Mathematics
Islamic scholars during the Golden Age of Islam (8th to 14th centuries) expanded on Greek and Hindu mathematics. Al-Khwarizmi, in his seminal work "Al-Kitab al-Mukhtasar fi Hisab al-Jabr wal-Muqabala," introduced methods for solving quadratic equations, which inherently involve finding square roots.
Renaissance and Beyond
- Fibonacci: In the 13th century, Leonardo of Pisa, known as Fibonacci, introduced the method of finding square roots through his works, including the "Liber Abaci," which helped spread Hindu-Arabic numerals in Europe.
- 16th Century Mathematicians: Mathematicians like Gerolamo Cardano and Rafael Bombelli further developed algebraic methods to solve equations involving square roots, enhancing the precision and usability of these calculations.
Modern Era
With the advent of calculus and the formalization of algebra, the concept of square roots became more refined. The use of logarithms and later digital computers allowed for highly precise calculations, making square roots a fundamental operation in various fields, from engineering to computer science.
The historical journey of square roots is a testament to human ingenuity and the collaborative nature of mathematical discovery. Each civilization built upon the knowledge of its predecessors, leading to the advanced mathematical techniques we use today.
Frequently Asked Questions About Square Roots
Here are some frequently asked questions about square roots, including the square root of 5:
-
What is the square root of 5?
The square root of 5 is approximately \( \sqrt{5} \approx 2.236 \). It is an irrational number, meaning it cannot be expressed as a simple fraction.
-
Is the square root of 5 a real number?
Yes, the square root of 5 is a real number. It is a positive value and falls between the integers 2 and 3 on the number line.
-
Can the square root of 5 be simplified further?
No, the square root of 5 is already in its simplest form. It cannot be simplified into a smaller radical or a rational number.
-
How do you add square roots, such as \( \sqrt{5} + \sqrt{5} \)?
When adding square roots, you can only combine like terms. Since \( \sqrt{5} \) and \( \sqrt{5} \) are like terms, you can add them directly:
\[ \sqrt{5} + \sqrt{5} = 2\sqrt{5} \]
This simplifies to approximately \( 2 \times 2.236 = 4.472 \).
-
Does \( \sqrt{5} + \sqrt{5} \) equal \( \sqrt{10} \)?
No, \( \sqrt{5} + \sqrt{5} \) does not equal \( \sqrt{10} \). Instead:
\[ \sqrt{5} + \sqrt{5} = 2\sqrt{5} \approx 4.472 \]
Whereas:
\[ \sqrt{10} \approx 3.162 \]
The two values are not equal.
-
What is the historical significance of square roots?
The concept of square roots has been studied since ancient times. Early civilizations, such as the Babylonians and Greeks, developed methods for approximating square roots. The symbol for the square root, \( \sqrt{} \), was first used in the 16th century by mathematician Christoph Rudolff.
These questions and answers aim to clarify common doubts and provide a better understanding of square roots and their properties.
Căn bậc hai của 5 được đơn giản hóa
READ MORE:
Cách tìm căn bậc hai của 5 bằng phương pháp chia dài / Căn bậc hai của 5 / Tìm căn bậc hai của 5