Topic what is the square root of 5: The square root of 5 is a fascinating and important mathematical constant, represented as √5. It's an irrational number with intriguing properties and applications across various fields. In this article, we explore its definition, calculation methods, and real-world uses, making the complex concept of √5 accessible and engaging for everyone.
Table of Content
- Understanding the Square Root of 5
- Introduction to the Square Root of 5
- Mathematical Definition and Notation
- Decimal Representation and Properties
- Methods to Calculate the Square Root of 5
- Geometric Interpretation and Applications
- Practical Examples and Usage in Real Life
- Relations to Other Mathematical Concepts
- Historical Context and Significance
- Visual Representations and Diagrams
- Frequently Asked Questions (FAQs)
- Additional Resources and Further Reading
- YOUTUBE:
Understanding the Square Root of 5
The square root of 5 is an important mathematical constant. It is an irrational number, which means it cannot be expressed as a simple fraction and its decimal representation goes on forever without repeating.
Mathematical Representation
In mathematical notation, the square root of 5 is written as \( \sqrt{5} \). Its approximate value is:
\[ \sqrt{5} \approx 2.23606797749979 \]
Calculation Methods
There are several methods to calculate the square root of 5, including:
- Long Division Method
- Prime Factorization
- Using a Calculator
Geometric Interpretation
Geometrically, \( \sqrt{5} \) can be visualized as the diagonal length of a rectangle with sides of 1 and 2 units, following the Pythagorean theorem:
\[ \text{Diagonal} = \sqrt{1^2 + 2^2} = \sqrt{5} \]
This relationship is used in various geometric constructions and problems.
Properties and Applications
- \( \sqrt{5} \) is an irrational number.
- It appears in the formulas for certain trigonometric constants and in solving quadratic equations.
- It is also related to the golden ratio \( \phi \), where \( \phi = \frac{1 + \sqrt{5}}{2} \).
Decimal Expansion
The decimal expansion of \( \sqrt{5} \) is non-terminating and non-repeating. Here are the first few digits:
2.23606797749979...
Practical Example
In practical scenarios, \( \sqrt{5} \) might be used to find distances or in various engineering problems. For instance, if you need to find the length of a diagonal of a rectangle with sides of 1 meter and 2 meters, you use \( \sqrt{5} \) meters.
Table of Common Square Roots
| Number | Square Root |
|---|---|
| 1 | 1 |
| 2 | 1.414 |
| 3 | 1.732 |
| 4 | 2 |
| 5 | 2.236 |
Related Formulas and Identities
The square root of 5 often appears in various mathematical formulas and identities, including:
- The quadratic formula: \[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
- In the expression for the golden ratio: \[ \phi = \frac{1 + \sqrt{5}}{2} \]
- Trigonometric identities involving half-angle formulas.
Visual Representation
Below is a visual representation of \( \sqrt{5} \) using a right triangle:


READ MORE:
Introduction to the Square Root of 5
The square root of 5, denoted as \( \sqrt{5} \), is a unique and intriguing number in mathematics. It's classified as an irrational number, meaning it cannot be exactly represented as a simple fraction and its decimal expansion is infinite and non-repeating. Understanding the square root of 5 involves delving into its mathematical properties, geometric applications, and its significance in various fields.
- Mathematical Definition: The square root of 5 is the number which, when multiplied by itself, equals 5. Symbolically, this is written as \( \sqrt{5} \times \sqrt{5} = 5 \).
- Approximate Value: The approximate value of \( \sqrt{5} \) is 2.23606797749979, which continues indefinitely without repeating.
- Geometric Significance: Geometrically, \( \sqrt{5} \) can be visualized as the length of the diagonal of a rectangle with sides of 1 unit and 2 units, derived using the Pythagorean theorem: \( \sqrt{1^2 + 2^2} = \sqrt{5} \).
- Calculation Methods: There are various methods to approximate \( \sqrt{5} \):
- Long Division Method: A manual method involving successive approximations.
- Newton's Method: An iterative process to find increasingly accurate approximations.
- Using Calculators: Modern tools can instantly provide precise values.
- Applications: The square root of 5 appears in many mathematical contexts, such as in trigonometric identities and in solving quadratic equations. It also has practical applications in engineering and physics.
Exploring \( \sqrt{5} \) opens a window into the broader world of irrational numbers and their fundamental role in both theoretical and applied mathematics.
Mathematical Definition and Notation
The square root of 5, expressed as \( \sqrt{5} \), is a fundamental concept in mathematics. It represents the value that, when multiplied by itself, equals 5. This section explores its definition, properties, and various ways to represent it.
- Definition:
The square root of a number \( x \) is a value \( y \) such that \( y^2 = x \). In the case of 5, the square root is the number \( y \) where \( y \times y = 5 \). Thus, \( \sqrt{5} \) is the positive number that satisfies this condition.
- Notation:
Mathematically, the square root of 5 is denoted by the radical symbol as \( \sqrt{5} \). This is the most common way to represent the principal (positive) square root. For more precise mathematical notation, we sometimes use the exponent notation: \( 5^{0.5} \) or \( 5^{1/2} \).
- Properties:
- \( \sqrt{5} \) is an irrational number, which means it cannot be exactly expressed as a fraction of two integers. Its decimal form is infinite and non-repeating.
- The value of \( \sqrt{5} \) lies between 2 and 3, closer to 2.236. This is because \( 2^2 = 4 \) and \( 3^2 = 9 \).
- It is related to the golden ratio \( \phi \), which is \( \frac{1 + \sqrt{5}}{2} \), a significant number in mathematics, art, and nature.
- Calculating \( \sqrt{5} \):
While the exact value of \( \sqrt{5} \) cannot be determined without approximation, several methods can be used to find its value to a desired degree of accuracy:
- Long Division Method: A manual process that provides successive approximations of \( \sqrt{5} \).
- Newton's Method (or Heron's Method): An iterative technique where the value is refined using the formula \( x_{n+1} = \frac{1}{2}\left(x_n + \frac{5}{x_n}\right) \).
- Using Digital Tools: Modern calculators and computer algorithms can compute \( \sqrt{5} \) to millions of decimal places.
- Tabular Representation:
n Approximation 1 2.2 2 2.24 3 2.236 4 2.2361 5 2.23607
Understanding the mathematical definition and notation of \( \sqrt{5} \) provides a solid foundation for exploring its applications and significance in various branches of mathematics and science.
Decimal Representation and Properties
The square root of 5, denoted as \( \sqrt{5} \), is an irrational number. This means its decimal representation is non-terminating and non-repeating, extending infinitely without forming a predictable pattern. Exploring its decimal form and properties provides valuable insights into its nature and applications.
- Decimal Expansion:
The decimal expansion of \( \sqrt{5} \) begins as 2.23606797749979... and continues infinitely. It cannot be precisely expressed as a finite or repeating decimal, underscoring its classification as an irrational number.
- Approximation:
For practical purposes, \( \sqrt{5} \) is often approximated to a few decimal places. Here are some common approximations:
Approximation Decimal Value Rounded to 2 decimal places 2.24 Rounded to 3 decimal places 2.236 Rounded to 5 decimal places 2.23607 Rounded to 10 decimal places 2.2360679775 - Properties:
- Irrational Nature: \( \sqrt{5} \) cannot be exactly represented as a ratio of two integers. Its decimal form continues infinitely without repeating.
- Positive and Negative Roots: While \( \sqrt{5} \) commonly refers to the positive square root, it also has a negative counterpart, \(-\sqrt{5} \), satisfying the equation \( x^2 = 5 \).
- Relationship to Rational Approximations: Rational approximations of \( \sqrt{5} \), such as 2.236, are often used for quick calculations, though they only offer an approximate value.
- Connection to Golden Ratio: \( \sqrt{5} \) is intimately related to the golden ratio \( \phi \), which can be expressed as \( \phi = \frac{1 + \sqrt{5}}{2} \). This relationship is significant in mathematics, art, and nature.
- Visualization:
To better understand \( \sqrt{5} \), consider its position on the number line:
- It lies between 2 and 3, closer to 2.24.
- In a geometric context, it represents the diagonal of a rectangle with sides 1 and 2 units long, demonstrating its practical application in geometry.
The infinite and non-repeating nature of \( \sqrt{5} \)'s decimal expansion highlights its complexity and importance as an irrational number. Its properties and approximations make it a valuable tool in various mathematical and scientific applications.
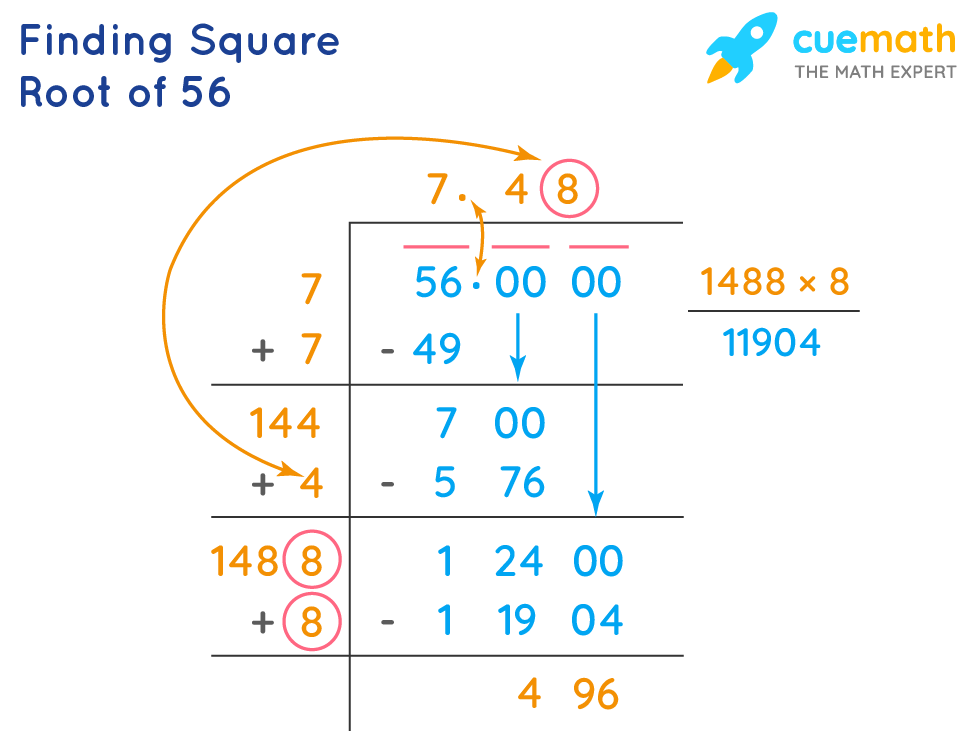
Methods to Calculate the Square Root of 5
Calculating the square root of 5 can be approached through several methods, each offering varying degrees of precision and complexity. Whether using manual techniques or leveraging modern digital tools, these methods provide valuable insights into obtaining the value of \( \sqrt{5} \).
- Long Division Method:
The long division method is a manual technique to find square roots with step-by-step division. Here’s how it works for \( \sqrt{5} \):
- Pair the digits of 5 from right to left (since 5 is a single digit, it's just considered as 5.0).
- Determine the largest number whose square is less than or equal to 5. In this case, 2 because \( 2^2 = 4 \).
- Subtract 4 from 5 to get a remainder of 1. Bring down a pair of zeros to make it 100.
- Double the divisor (2), getting 4. Find the largest digit (x) such that \( 4x \times x \) is less than or equal to 100. Here, \( x = 2 \) because \( 42 \times 2 = 84 \).
- Repeat the process with the new divisor and remainder to find further decimal places.
- Newton's Method (Heron's Method):
Newton's method is an iterative approach that refines an initial guess to approximate square roots. Follow these steps to find \( \sqrt{5} \):
- Start with an initial guess \( x_0 \). For \( \sqrt{5} \), 2 is a reasonable starting point.
- Use the formula \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{5}{x_n} \right) \) to find the next approximation.
- Repeat the process until the desired accuracy is achieved. For example:
- Starting with \( x_0 = 2 \)
- \( x_1 = \frac{1}{2} \left( 2 + \frac{5}{2} \right) = 2.25 \)
- \( x_2 = \frac{1}{2} \left( 2.25 + \frac{5}{2.25} \right) \approx 2.236 \)
- Using Calculators:
Modern calculators and software tools provide quick and accurate values for \( \sqrt{5} \). Most digital calculators have a dedicated square root function that can instantly compute \( \sqrt{5} \). For instance, entering 5 and pressing the square root button gives approximately 2.236067977.
- Approximation by Series Expansion:
Advanced mathematical methods like Taylor series or binomial expansion can also approximate \( \sqrt{5} \). For example, using the binomial expansion:
\[ \sqrt{5} = \sqrt{4 + 1} = 2 \left( 1 + \frac{1}{4} \right)^{1/2} \]
Expanding this using the binomial series gives a progressively accurate approximation:
\[ 2 \left( 1 + \frac{1}{8} - \frac{1}{128} + \cdots \right) \approx 2.236 \]
These methods demonstrate various ways to calculate or approximate the square root of 5, each suitable for different contexts and levels of precision. Whether using simple manual techniques or sophisticated mathematical tools, understanding these methods enriches our grasp of irrational numbers like \( \sqrt{5} \).

Geometric Interpretation and Applications
The square root of 5, \( \sqrt{5} \), holds significant geometric meaning and finds applications in various mathematical and real-world contexts. Understanding its geometric interpretation helps in visualizing its value and its utility in different fields.
- Geometric Interpretation:
In geometry, \( \sqrt{5} \) can be visualized using the Pythagorean theorem. Consider a right triangle with legs of lengths 1 and 2. The hypotenuse \( c \) can be found using:
\[ c = \sqrt{1^2 + 2^2} = \sqrt{1 + 4} = \sqrt{5} \]
This shows that the length of the diagonal of a rectangle with sides 1 unit and 2 units is \( \sqrt{5} \). This geometric perspective makes \( \sqrt{5} \) a crucial factor in understanding distances in multi-dimensional spaces.
- Golden Ratio Connection:
\( \sqrt{5} \) is closely related to the golden ratio \( \phi \), which is defined as \( \phi = \frac{1 + \sqrt{5}}{2} \). This ratio appears in various aspects of art, architecture, and nature, such as in the proportions of the Parthenon or the arrangement of leaves on a stem. The presence of \( \sqrt{5} \) in this formula underlines its importance in natural and aesthetic symmetries.
- Trigonometric Applications:
In trigonometry, \( \sqrt{5} \) appears in the simplification of certain identities and expressions. For example, it is used in the derivation of some specific angle relationships in polygonal and circular geometry.
- Applications in Physics:
In physics, the square root of 5 is used in the equations describing wave dynamics and quantum mechanics. It helps in solving problems involving distance calculations and analyzing the properties of waves and oscillations.
- Engineering and Design:
Engineers use \( \sqrt{5} \) in structural design and optimization. For example, in the design of components and systems where precise measurements are crucial, such as in the calculation of tolerances and material strengths.
Understanding the geometric interpretation and applications of \( \sqrt{5} \) enriches its mathematical significance and demonstrates its practical utility in various fields. From visualizing distances to solving complex problems in science and engineering, \( \sqrt{5} \) remains a fundamental constant in both theoretical and applied mathematics.
Practical Examples and Usage in Real Life
The square root of 5, \( \sqrt{5} \approx 2.236 \), is not only a fundamental mathematical constant but also appears in various practical and real-life applications. Its presence in nature, engineering, and everyday calculations underscores its importance beyond theoretical mathematics.
- Architectural Design:
In architecture, \( \sqrt{5} \) is utilized to determine proportions and aesthetic dimensions. For instance, when designing structures that incorporate the golden ratio \( \phi \), \( \sqrt{5} \) becomes essential, as \( \phi = \frac{1 + \sqrt{5}}{2} \). This ratio is often applied to achieve visually pleasing and harmonious designs, such as in the layout of buildings and the spacing of structural elements.
- Engineering and Construction:
Engineers use \( \sqrt{5} \) in various calculations, including determining the diagonal length of rectangular components. For example, in the design of a beam that needs to span a rectangular space, knowing \( \sqrt{5} \) helps in accurately computing the diagonal support needed for stability.
- Physics and Wave Mechanics:
In physics, \( \sqrt{5} \) appears in equations related to wave phenomena and oscillatory systems. For instance, the frequency and wavelength of waves in certain contexts can involve \( \sqrt{5} \), influencing how engineers design acoustic systems or analyze wave propagation in different media.
- Computer Graphics and Animation:
In computer graphics, precise calculations involving \( \sqrt{5} \) are required to render realistic images and animations. For example, determining the distance between points in a 3D space or scaling objects proportionally often involves square roots, including \( \sqrt{5} \), to maintain correct perspectives and proportions.
- Finance and Economics:
Financial analysts sometimes use \( \sqrt{5} \) in models for predicting growth rates and calculating compound interest. For instance, in risk assessment and portfolio optimization, understanding how variables grow geometrically can involve square root calculations.
- Nature and Biology:
In nature, the value \( \sqrt{5} \) is implicitly found in the Fibonacci sequence and the arrangement of leaves or petals on plants. This sequence often describes patterns of growth and structure in biological organisms, illustrating how mathematical constants like \( \sqrt{5} \) are embedded in natural processes.
- Everyday Mathematics:
In everyday life, \( \sqrt{5} \) might be used in simple distance calculations. For instance, if you need to find the diagonal of a rectangular area with sides 1 and 2 units long (such as a rectangular screen or a piece of furniture), the diagonal length would be \( \sqrt{5} \).
The ubiquity of \( \sqrt{5} \) across different domains highlights its versatility and critical role in solving practical problems. Whether in complex engineering designs or simple daily measurements, the square root of 5 offers a bridge between abstract mathematics and tangible applications.
Relations to Other Mathematical Concepts
The square root of 5 (√5) is an intriguing number with various connections to other mathematical concepts. Here, we will explore its relationships with algebra, geometry, number theory, and more.
Algebraic Properties
√5 is an irrational number, meaning it cannot be expressed as a simple fraction and its decimal expansion is non-repeating and infinite. This places √5 alongside other well-known irrational numbers like √2 and √3. In algebra, it often appears in quadratic equations and solutions to polynomial equations.
Geometric Interpretation
Geometrically, √5 can be visualized as the diagonal length of a rectangle with sides of 1 and 2 units, derived from the Pythagorean theorem:
This is significant in constructing dynamic rectangles, such as the root-five rectangle, used in design and architecture.
Golden Ratio and Fibonacci Sequence
The square root of 5 is intrinsically linked to the golden ratio (φ). The golden ratio is given by:
This ratio is prominent in the Fibonacci sequence, where the ratio of successive Fibonacci numbers converges to φ. Furthermore, the limit of the quotient of the nth Lucas number (Ln) and the nth Fibonacci number (Fn) equals √5:
Trigonometry
In trigonometry, √5 is found in exact trigonometric constants, particularly in the formulae involving cosines and sines of specific angles. These relationships are used in solving various trigonometric equations and in simplifying expressions.
Applications in Advanced Mathematics
√5 appears in advanced mathematical contexts, such as continued fractions and series. For example, the continued fraction representation of √5 reveals its unique properties and convergence characteristics.
Summary
The square root of 5 is not just a simple irrational number; it bridges various mathematical concepts from geometry to algebra and number theory. Understanding its properties and relationships enhances comprehension of more complex mathematical structures.
Historical Context and Significance
The square root of 5, denoted as \( \sqrt{5} \), has been a topic of interest in mathematics for centuries, spanning several historical periods and cultures.
Babylonian Mathematics
Early instances of sophisticated mathematical knowledge can be traced back to the Babylonians around 1800-1600 BC. They used a base-60 numeral system to perform complex calculations, including approximations of square roots. The Babylonian clay tablets, such as YBC 7289, show their advanced understanding of quadratic equations and square roots, demonstrating methods that resemble our modern techniques of division and averaging to approximate these values.
Greek Mathematics
In ancient Greece, the study of irrational numbers, including \( \sqrt{5} \), was significantly advanced by mathematicians such as Pythagoras and his followers. The Pythagoreans initially believed that all numbers were rational, but the discovery of irrational numbers like \( \sqrt{2} \) and \( \sqrt{5} \) challenged their worldview. This discovery was a profound moment in mathematical history, as it led to a deeper understanding of number theory and the development of more abstract mathematical concepts.
Spiral of Theodorus
The Greek mathematician Theodorus of Cyrene used the square root of numbers, including \( \sqrt{5} \), to construct what is now known as the Spiral of Theodorus. This geometric representation involves drawing successive right triangles, each with a hypotenuse representing the square root of an integer. The segment representing \( \sqrt{5} \) is part of this continuous spiral, which visually demonstrates the increasing values of these square roots.
Medieval Islamic Mathematics
During the Islamic Golden Age, mathematicians made significant contributions to algebra and number theory. They translated and expanded upon Greek texts, preserving and enhancing the knowledge of irrational numbers. Islamic scholars like Al-Khwarizmi and Omar Khayyam worked on methods for approximating square roots and solving quadratic equations, thereby influencing the mathematical understanding of numbers like \( \sqrt{5} \).
Modern Mathematics
In modern times, \( \sqrt{5} \) continues to be a subject of interest, especially in fields such as algebra, number theory, and geometry. Its properties are used in various mathematical proofs and applications, including the study of quadratic fields and Diophantine equations.
The historical journey of \( \sqrt{5} \) reflects the evolving nature of mathematical knowledge, from ancient empirical methods to modern theoretical frameworks, illustrating its enduring significance in the broader context of mathematical discovery and education.

Visual Representations and Diagrams
The square root of 5 (\(\sqrt{5}\)) can be represented visually in various ways, enhancing our understanding of its properties and applications. Below are several methods to visualize \(\sqrt{5}\):
Number Line Representation
On a number line, \(\sqrt{5}\) is positioned between the integers 2 and 3, as its approximate value is 2.236. This helps in understanding its relative size compared to other numbers.

Geometric Interpretation
A common geometric representation involves using the Pythagorean theorem. Consider a right triangle with legs of lengths 1 and 2 units. The length of the hypotenuse will be \(\sqrt{5}\), as derived from the equation:
\[
\sqrt{1^2 + 2^2} = \sqrt{1 + 4} = \sqrt{5}
\]

Root-5 Rectangle
A rectangle with side lengths in the ratio 1:\(\sqrt{5}\) is known as a root-5 rectangle. This is part of a series of root rectangles used in dynamic symmetry. The visual below shows a root-5 rectangle:

Visualizing \(\sqrt{5}\) with Squares
Visualizing \(\sqrt{5}\) can also be done by considering the area of a square with side length \(\sqrt{5}\). This square would have an area of 5 square units.

Relation to the Golden Ratio
The square root of 5 is intricately connected to the golden ratio (\(\phi\)), which can be expressed as \(\phi = \frac{1 + \sqrt{5}}{2}\). This relationship can be visualized through the construction of a golden rectangle, where the ratio of the longer side to the shorter side is \(\phi\).

These visual representations help in comprehending the mathematical significance and the practical applications of the square root of 5 in geometry and other fields.
Frequently Asked Questions (FAQs)
Here are some frequently asked questions about the square root of 5, along with detailed answers to help you understand this mathematical concept better.
-
What is the square root of 5?
The square root of 5 is a number which, when multiplied by itself, equals 5. It is represented as \( \sqrt{5} \) and is approximately equal to 2.236.
-
Is the square root of 5 a rational or irrational number?
The square root of 5 is an irrational number. This means it cannot be expressed as a simple fraction and its decimal representation is non-repeating and non-terminating.
-
How can we calculate the square root of 5?
The square root of 5 can be calculated using various methods such as:
- Using a calculator for a quick and accurate value.
- Using the long division method to manually compute the value.
- Using iterative methods like the Newton-Raphson method for approximations.
-
What are the properties of the square root of 5?
The square root of 5 has the following properties:
- It is a positive real number.
- Its square (multiplying it by itself) gives the original number 5.
- It is an irrational number.
-
How is the square root of 5 used in geometry?
In geometry, the square root of 5 can be used in various contexts, such as calculating the diagonal of a rectangle with side lengths in a specific ratio or in the Pythagorean theorem.
-
Can the square root of 5 be represented on a number line?
Yes, the square root of 5 can be represented on a number line. It lies between the numbers 2 and 3, closer to 2.2. Precise plotting involves using its approximate value of 2.236.
-
What are some real-life applications of the square root of 5?
The square root of 5 is used in various fields such as physics, engineering, and computer science, especially in problems involving quadratic equations, optimization, and complex calculations.
Additional Resources and Further Reading
For those interested in deepening their understanding of the square root of 5 and related mathematical concepts, here are some valuable resources and further reading materials:
- Square Root Information and Calculators: Online tools such as square-root.net offer detailed information about the square root of 5, including calculators for various roots and explanations of their properties. These can be useful for exploring the mathematical background and applications of square roots.
- Mathematical Articles and Tutorials: Websites like mathwarehouse.com provide in-depth articles on the simplest radical forms of various square roots, including step-by-step solutions and visual aids to help understand the concepts better.
- Educational Videos: Platforms like Khan Academy and YouTube have numerous educational videos explaining the concept of square roots, including the square root of 5, in an easy-to-understand format.
- Books:
- The Joy of x: A Guided Tour of Math, from One to Infinity by Steven Strogatz – This book provides a broad overview of mathematical concepts, including square roots, explained in an engaging and accessible way.
- Principles of Mathematics by Carl Barnett Allendoerfer and Cletus Oakley – A more detailed mathematical textbook that covers the properties and applications of square roots among other fundamental concepts.
- Academic Papers: For those looking for more rigorous mathematical discussions, academic papers and journals can be a rich resource. Accessing databases like JSTOR or Google Scholar with search terms such as "square root of 5" can yield valuable scholarly articles.
By exploring these resources, you can gain a comprehensive understanding of the square root of 5 and its place within the broader context of mathematics.
Giải Thích Căn Bậc Hai Của 5
READ MORE:
Cách Tìm Căn Bậc Hai Của 5 Bằng Phương Pháp Chia Dài / Căn Bậc Hai Của 5 / Tìm Căn Bậc Hai Của 5