Topic square root of 5 times 2: The square root of 5 times 2 is a mathematical expression that can be simplified for easier calculation. Understanding this expression is crucial for various mathematical problems. In this article, we will explore the simplification process, provide examples, and demonstrate practical applications of this concept.
Table of Content
- Square Root of 5 Times 2
- Introduction to Square Roots
- Calculating Square Roots
- Simplifying Square Roots
- Examples of Simplifying Square Roots
- Using Square Root Calculators
- Practical Applications of Square Roots
- YOUTUBE: Phần trăm của căn bậc hai của 2 (5 lần căn bậc hai của 2) =? Một bài toán cơ bản mà nhiều người có thể sẽ trả lời sai. Xem để tìm hiểu cách giải đúng!
Square Root of 5 Times 2
The mathematical expression "square root of 5 times 2" can be represented and simplified using the properties of square roots and radicals.
Mathematical Representation
The expression can be written as:
\[\sqrt{5} \times 2\]
Which can be simplified further by understanding the multiplication of a square root and a whole number:
\[\sqrt{5} \times 2 = 2\sqrt{5}\]
Steps to Simplify
- Identify the terms: In this case, the terms are the square root of 5 and the number 2.
- Multiply the whole number by the square root term directly: \(2 \times \sqrt{5}\).
- The expression \(2\sqrt{5}\) is already in its simplest form.
Example Calculation
Consider another example for better understanding:
- Simplify \(\sqrt{6} \times \sqrt{15}\):
- Combine using the product rule for radicals: \(\sqrt{6 \times 15} = \sqrt{90}\).
- Factor inside the square root to simplify: \(\sqrt{90} = \sqrt{9 \times 10} = 3\sqrt{10}\).
Additional Information
The square root calculator on various educational websites can help in simplifying and verifying these calculations. These tools allow you to input any radical expressions and see step-by-step solutions for better understanding.
| Expression | Step-by-Step Simplification | Result |
|---|---|---|
| \(\sqrt{5} \times 2\) | Direct multiplication | \(2\sqrt{5}\) |
| \(\sqrt{6} \times \sqrt{15}\) | \(\sqrt{90} = \sqrt{9 \times 10} = 3\sqrt{10}\) | \(3\sqrt{10}\) |
Useful Resources
For more detailed calculations and practice problems, check out these online calculators and educational resources:
READ MORE:
Introduction to Square Roots
Square roots are a fundamental concept in mathematics, representing a value that, when multiplied by itself, gives the original number. The notation for the square root is the radical symbol √, followed by the number we want to find the root of. Understanding square roots is crucial for solving various mathematical problems, including those involving algebra, geometry, and calculus.
The square root of a number \( x \) is written as \( \sqrt{x} \). For example, the square root of 25 is 5, because \( 5 \times 5 = 25 \). Some numbers, known as perfect squares, have integer square roots. These include numbers like 1, 4, 9, 16, 25, and so on. However, not all numbers are perfect squares. For instance, the square root of 5 is an irrational number, approximately equal to 2.236.
To simplify square roots, we look for factors of the number under the radical that are perfect squares. For instance, to simplify \( \sqrt{20} \), we recognize that 20 can be factored into 4 and 5, where 4 is a perfect square. Therefore:
\[ \sqrt{20} = \sqrt{4 \times 5} = \sqrt{4} \times \sqrt{5} = 2\sqrt{5} \]
Square roots also follow specific properties that make calculations easier. One such property is:
\[ \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \]
This property allows us to break down more complex square roots into simpler components.
Understanding these basics helps in solving more complex mathematical problems and is foundational for higher-level math and science courses.
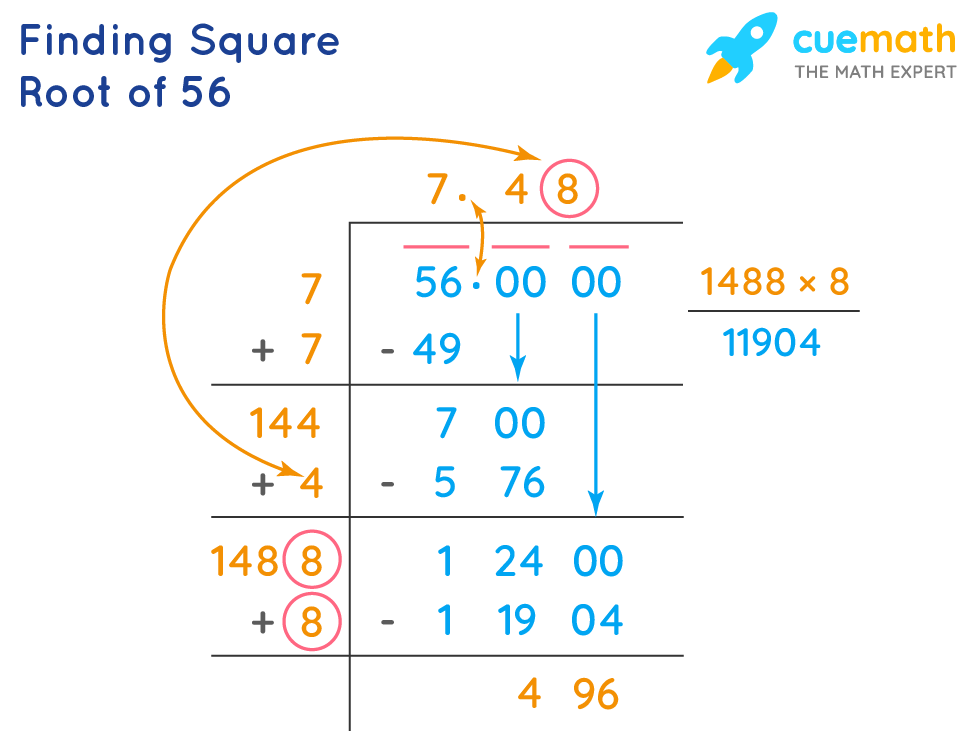
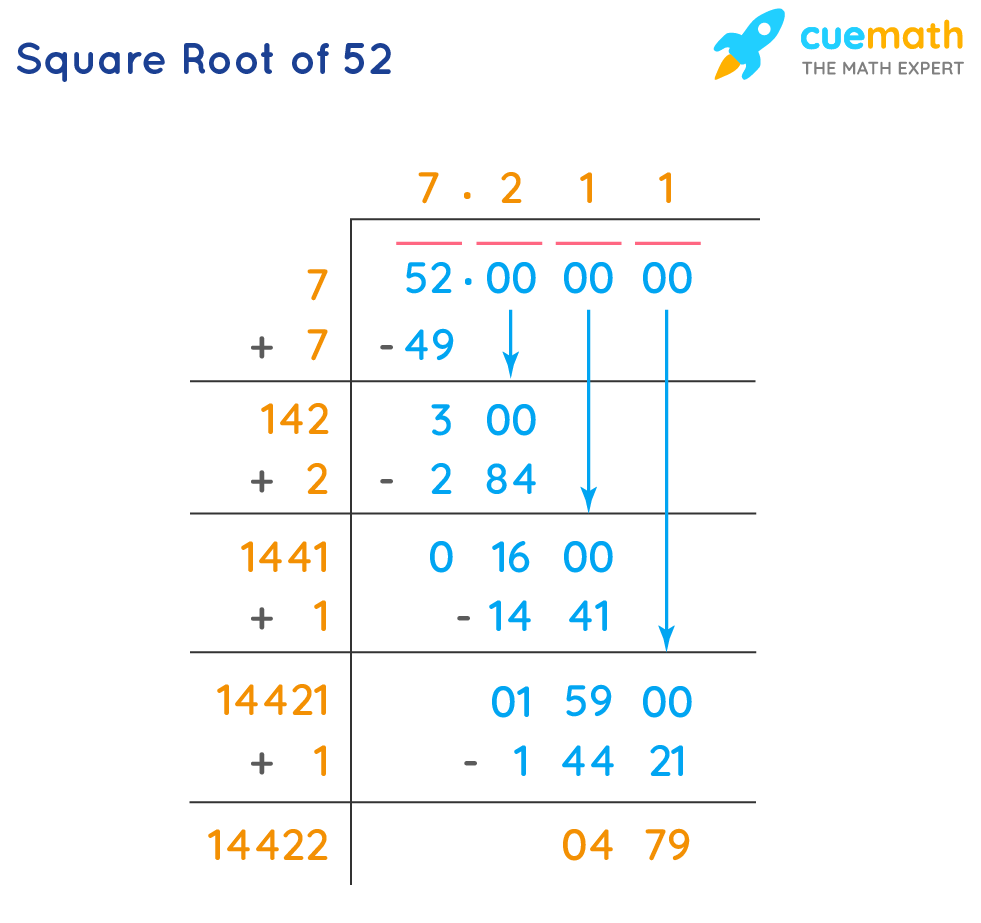
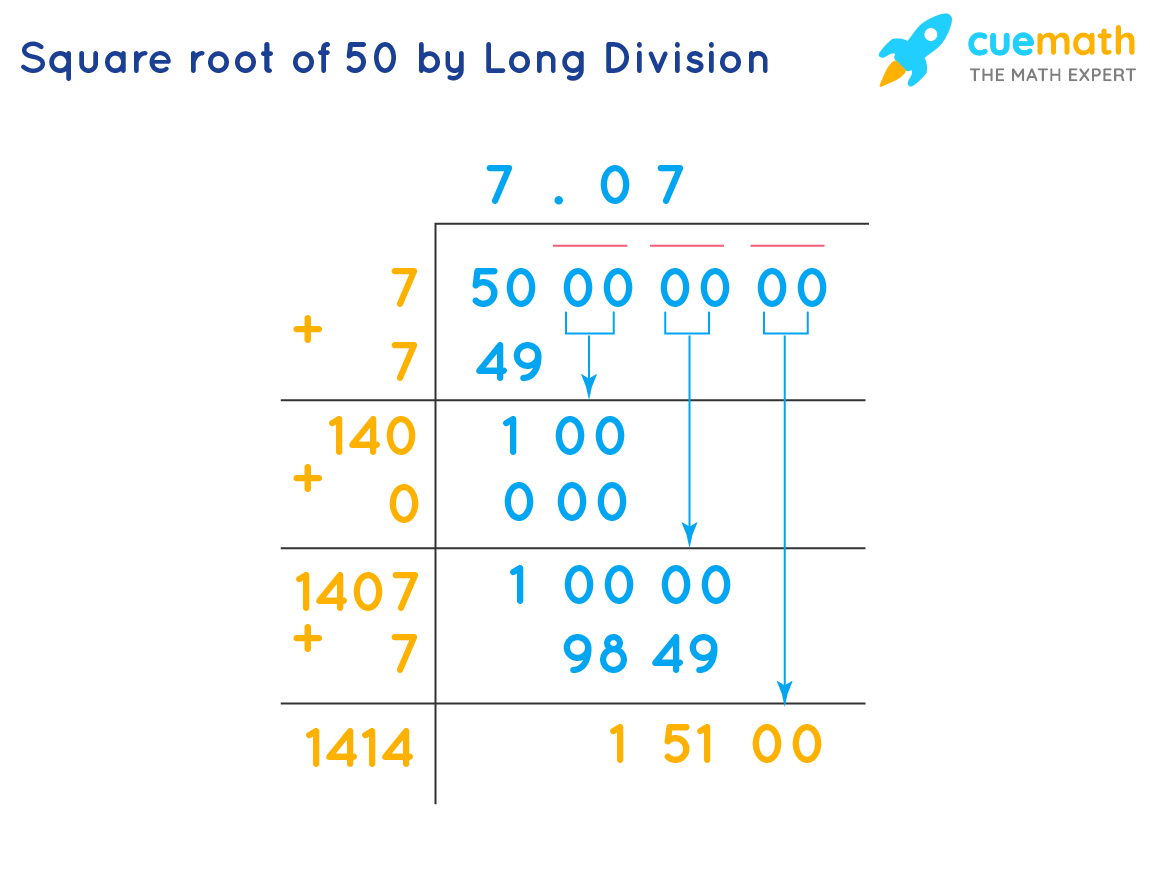
Calculating Square Roots
Calculating the square root of a number involves finding a value which, when multiplied by itself, yields the original number. The square root is denoted by the radical symbol √. For instance, the square root of 25 is 5, because \(5 \times 5 = 25\). Here is a step-by-step guide to calculating square roots:
- Identify the number you want to find the square root of. This number is called the radicand.
- If the radicand is a perfect square, its square root is an integer. For example, √36 = 6, since \(6 \times 6 = 36\).
- If the radicand is not a perfect square, you can simplify it by factoring out perfect squares. For example:
- To simplify √50, note that 50 = 25 × 2. Hence, √50 = √(25 × 2) = √25 × √2 = 5√2.
- For √18, recognize that 18 = 9 × 2. Thus, √18 = √(9 × 2) = √9 × √2 = 3√2.
- Use a calculator for non-perfect squares to get a decimal approximation. For example, √5 ≈ 2.236.
The property of square roots that simplifies multiplication is:
\[ \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \]
This property is useful for breaking down more complex square roots into simpler terms. For example:
\[ \sqrt{10} = \sqrt{2 \times 5} = \sqrt{2} \times \sqrt{5} \]
Using these steps, you can accurately calculate and simplify square roots, aiding in the solving of various mathematical problems.
Simplifying Square Roots
Simplifying square roots involves reducing the radicand (the number inside the square root) to its simplest form. This process makes calculations easier and expressions more understandable. Below is a step-by-step guide to simplifying square roots.
-
Identify Perfect Square Factors: Start by identifying the perfect square factors of the radicand. Perfect squares are numbers like 1, 4, 9, 16, 25, etc.
- Example: To simplify \(\sqrt{12}\), notice that 12 is \(4 \times 3\), and 4 is a perfect square.
-
Apply the Product Rule: Use the property \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\).
- Example: \(\sqrt{12} = \sqrt{4 \times 3} = \sqrt{4} \times \sqrt{3}\).
-
Simplify the Perfect Square: Take the square root of the perfect square factor.
- Example: \(\sqrt{4} = 2\), so \(\sqrt{12} = 2\sqrt{3}\).
-
Combine Like Terms: If you have multiple square root terms that are like terms, combine them.
- Example: \(2\sqrt{3} + 3\sqrt{3} = 5\sqrt{3}\).
For more complex expressions, follow these steps methodically. With practice, simplifying square roots will become second nature.
| Expression | Steps | Simplified Form |
| \(\sqrt{18}\) | \(\sqrt{18} = \sqrt{9 \times 2} = \sqrt{9} \times \sqrt{2} = 3\sqrt{2}\) | 3\(\sqrt{2}\) |
| \(\sqrt{50}\) | \(\sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} = 5\sqrt{2}\) | 5\(\sqrt{2}\) |
Examples of Simplifying Square Roots
Understanding how to simplify square roots is essential for solving various mathematical problems. Here are detailed examples to illustrate the process:
-
Simplify \(\sqrt{12}\)
- Factor 12 into its prime factors: \(12 = 4 \times 3\)
- Apply the square root to each factor: \(\sqrt{12} = \sqrt{4 \times 3}\)
- Use the property \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\): \(\sqrt{4} \times \sqrt{3}\)
- Simplify the square root of 4: \(2 \times \sqrt{3}\)
- Result: \(\sqrt{12} = 2\sqrt{3}\)
-
Simplify \(\sqrt{45}\)
- Factor 45 into its prime factors: \(45 = 9 \times 5\)
- Apply the square root to each factor: \(\sqrt{45} = \sqrt{9 \times 5}\)
- Use the property \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\): \(\sqrt{9} \times \sqrt{5}\)
- Simplify the square root of 9: \(3 \times \sqrt{5}\)
- Result: \(\sqrt{45} = 3\sqrt{5}\)
-
Simplify \(\sqrt{8}\)
- Factor 8 into its prime factors: \(8 = 4 \times 2\)
- Apply the square root to each factor: \(\sqrt{8} = \sqrt{4 \times 2}\)
- Use the property \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\): \(\sqrt{4} \times \sqrt{2}\)
- Simplify the square root of 4: \(2 \times \sqrt{2}\)
- Result: \(\sqrt{8} = 2\sqrt{2}\)
-
Simplify \(\sqrt{18}\)
- Factor 18 into its prime factors: \(18 = 9 \times 2\)
- Apply the square root to each factor: \(\sqrt{18} = \sqrt{9 \times 2}\)
- Use the property \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\): \(\sqrt{9} \times \sqrt{2}\)
- Simplify the square root of 9: \(3 \times \sqrt{2}\)
- Result: \(\sqrt{18} = 3\sqrt{2}\)
These examples demonstrate the systematic approach to simplifying square roots by factoring numbers into their prime components and applying the square root property to each factor. This method helps to simplify complex square root expressions efficiently.

Using Square Root Calculators
Square root calculators are essential tools for quickly and accurately determining the square root of any number. They simplify the process by providing instant results and are useful in various mathematical computations. Here's how to use a square root calculator step by step:
- Enter the number in the respective input field of the calculator.
- Click the "Find Square Root" button to initiate the calculation.
- The calculator will display the square root of the given number in the output field.
These calculators not only provide the square root but also simplify radical expressions, showing results in the simplest radical form. This is particularly useful for students and professionals dealing with complex mathematical problems.
For example, to find the square root of 5 times 2, you would enter 10 into the calculator. The output will show both the approximate decimal value and the simplified radical form if applicable.
Using square root calculators saves time and reduces the risk of manual calculation errors, making them an indispensable tool in both academic and professional settings.
Practical Applications of Square Roots
Square roots are utilized in various practical applications across different fields. Understanding how to compute and use square roots can enhance problem-solving skills and offer insights into real-world scenarios.
- Finance: Square roots are used to calculate stock market volatility, helping investors assess the risk of investments by determining the standard deviation of stock returns.
- Architecture: Engineers use square roots to determine the natural frequency of structures, such as bridges and buildings, to predict their response to environmental forces.
- Science: Square roots are employed in numerous scientific calculations, including velocity, radiation absorption, and sound intensity, facilitating technological and scientific advancements.
- Statistics: In statistics, square roots are used to calculate variance and standard deviation, which measure data spread and deviation from the mean, aiding in data analysis and decision-making.
- Geometry: Geometry problems involving right triangles and polygons often require the use of square roots to calculate areas, perimeters, and side lengths using the Pythagorean theorem.
- Computer Science: Square roots are crucial in algorithms for encryption, image processing, and game physics, enhancing computational efficiency and security.
- Cryptography: Digital signatures and secure communication systems rely on square roots to generate unique keys and authenticate data transactions.
- Navigation: Pilots and navigators use square roots to calculate distances between points on maps and estimate bearings, ensuring accurate and safe travel.
- Electrical Engineering: Square roots are essential in computing power, voltage, and current in circuits, aiding in the design of efficient electrical systems.
- Cooking: Scaling recipes accurately often involves using square roots to maintain the right balance of ingredients when adjusting quantities.
- Photography: The f-number of a camera lens, which controls light exposure, is related to the square of the aperture size, affecting image quality and brightness.
- Computer Graphics: Calculations for distances and vector lengths in 2D and 3D graphics frequently use square roots, ensuring accurate rendering and animations.
- Telecommunication: Signal strength in wireless communication decreases with distance according to the inverse square law, crucial for optimizing network performance.
READ MORE:
Phần trăm của căn bậc hai của 2 (5 lần căn bậc hai của 2) =? Một bài toán cơ bản mà nhiều người có thể sẽ trả lời sai. Xem để tìm hiểu cách giải đúng!
Phần trăm của căn bậc hai của 2 (5 lần căn bậc hai của 2) =? Một bài toán cơ bản NHIỀU người sẽ sai!