Topic semi-perimeter: Discover the fascinating world of geometry with our exploration of the semi-perimeter. This key concept, essential in understanding complex geometric formulas, unlocks a realm of mathematical wonders and practical applications, providing insights into the intricacies of shapes and spaces.
Table of Content
- What is the formula for calculating the semiperimeter of a polygon?
- Definition and Basic Concept of Semi-Perimeter
- Calculation and Formula of Semi-Perimeter in Triangles
- Application in Heron\"s Formula for Area Calculation
- Role in Determining the Circumradius and Inradius of Triangles
- YOUTUBE: Triangle Area Calculation using Inradius and Semiperimeter (visual proof)
- Examples and Solved Problems Involving Semi-Perimeter
- Extension to Quadrilaterals and Higher Polygons
- Relevance in Advanced Geometry and Trigonometry
- Practical Applications in Engineering and Design
- Frequently Asked Questions About Semi-Perimeter
What is the formula for calculating the semiperimeter of a polygon?
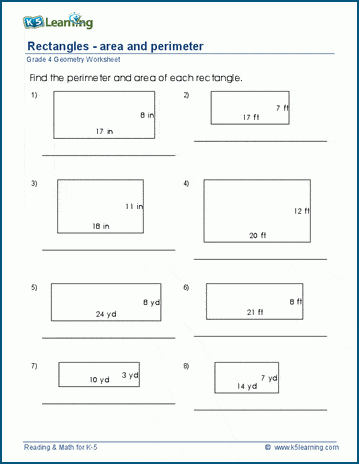
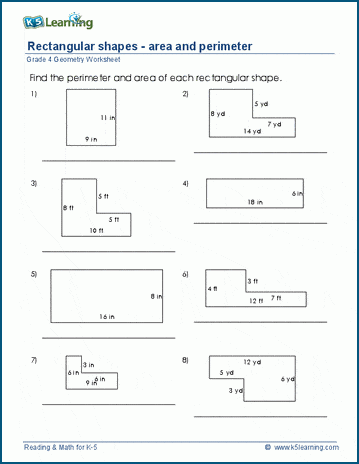
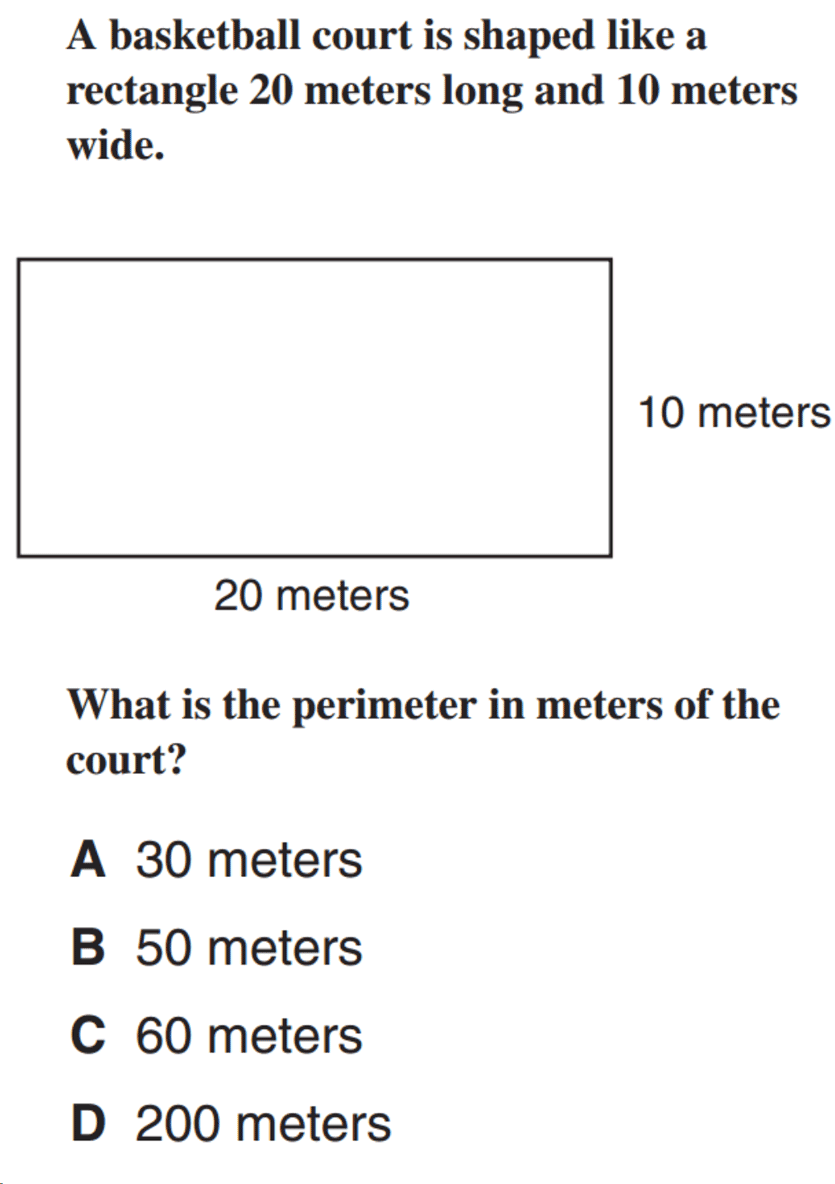
The formula for calculating the semiperimeter of a polygon is half the sum of the lengths of all its sides.
To calculate the semiperimeter, follow these steps:
- List the lengths of all the sides of the polygon.
- Add up all the side lengths.
- Divide the sum by 2.
Mathematically, the formula can be expressed as:
SemiPerimeter = (Side1 + Side2 + Side3 + ... + SideN)/2
where Side1, Side2, Side3, ... represent the lengths of the sides of the polygon, and N is the number of sides.
READ MORE:
Definition and Basic Concept of Semi-Perimeter
The semi-perimeter of a geometric shape is essentially half of its total perimeter. In mathematical terms, it is represented as \"s\", which is calculated as half the sum of the lengths of all sides of a polygon. For a triangle with sides a, b, and c, the semi-perimeter (s) is calculated as s = (a + b + c) / 2. This concept holds significant importance in geometry as it frequently appears in various formulas, particularly those involving triangles.
Understanding the semi-perimeter is crucial as it is used in several key geometric formulas. For instance, in triangles, it is integral to Heron\"s formula, which allows the calculation of a triangle\"s area from its side lengths. The formula for Heron\"s formula is A = sqrt[s(s-a)(s-b)(s-c)], where A is the area of the triangle. The semi-perimeter also appears in calculations involving the circumradius and inradius of triangles, playing a pivotal role in advanced geometric problems.
Moreover, the concept of semi-perimeter extends beyond triangles. It applies to quadrilaterals and other polygons, where it is used in formulas to calculate areas and other properties. In quadrilaterals, for example, the semi-perimeter is used in Brahmagupta\"s formula to find the area of cyclic quadrilaterals. The formula for the semi-perimeter of a quadrilateral with sides a, b, c, and d is s = (a + b + c + d) / 2.
- In the context of an isosceles triangle, if the length of the unequal side is known, the lengths of the equal sides can be derived using the semi-perimeter.
- For an equilateral triangle, the semi-perimeter helps in simplifying calculations as all sides are equal.
- In a right triangle, the semi-perimeter can be used to find the radius of the excircle on the hypotenuse.
Understanding the semi-perimeter thus provides a fundamental tool in solving a wide array of geometric problems and is essential for students and professionals dealing with geometric calculations.
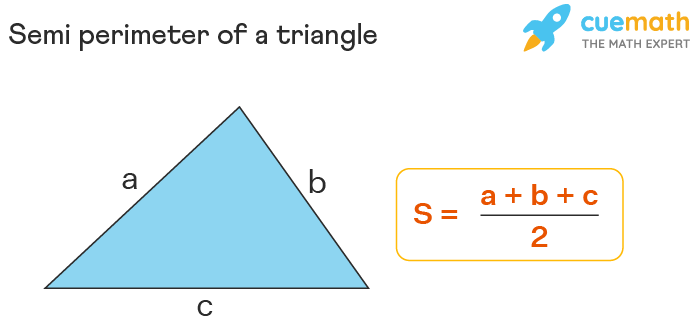
Calculation and Formula of Semi-Perimeter in Triangles
The calculation of the semi-perimeter of a triangle is crucial in solving various geometric problems. The semi-perimeter, denoted as \"s\", is defined as half the perimeter of a triangle. It is calculated using the formula s = (a + b + c) / 2, where a, b, and c represent the lengths of the sides of the triangle.
This formula is versatile and applies to different types of triangles:
- For an equilateral triangle, where all sides are equal (a = b = c), the semi-perimeter is s = 3a / 2.
- In an isosceles triangle, with two equal sides (a = b) and a different third side c, the semi-perimeter is s = (2a + c) / 2.
- For a right-angled triangle, it involves the base, height, and hypotenuse: s = (base + height + hypotenuse) / 2.
- In a scalene triangle, where all sides are different, the formula remains s = (a + b + c) / 2.
Additionally, the semi-perimeter is used in various geometric formulas, most notably Heron\"s formula for calculating the area of a triangle. Heron\"s formula is expressed as Area = √[s(s - a)(s - b)(s - c)], where \"s\" is the semi-perimeter.
Understanding these formulas allows for the calculation of other important geometric properties such as the inradius, circumradius, and the area of a triangle. The semi-perimeter serves as a fundamental element in these calculations, underlying the importance of mastering its computation.

Application in Heron\"s Formula for Area Calculation
Heron\"s formula is a significant application of the semi-perimeter concept in geometry, specifically in calculating the area of a triangle. This formula is especially useful when the lengths of all three sides of the triangle are known. The formula states that the area of a triangle (A) can be calculated using the formula A = √[s(s-a)(s-b)(s-c)], where \"s\" represents the semi-perimeter of the triangle, and \"a\", \"b\", and \"c\" are the lengths of the sides of the triangle.
The semi-perimeter (s) is calculated as half the sum of the side lengths of the triangle, using the formula s = (a + b + c) / 2. Heron\"s formula shows how the semi-perimeter is crucial in determining the area of a triangle without the need for any angle measurements.
Steps to use Heron\"s Formula:
- Calculate the semi-perimeter of the triangle using the lengths of its sides.
- Substitute the values of the side lengths and the semi-perimeter into Heron\"s formula.
- Compute the square root of the product obtained in the formula to find the area of the triangle.
This formula has broad applications in various fields, including architecture, engineering, and mathematics, providing a straightforward method to calculate the area of a triangle when the length of its sides are known.
Role in Determining the Circumradius and Inradius of Triangles
The semi-perimeter of a triangle plays a crucial role in determining two important geometric properties: the circumradius and the inradius. Understanding these concepts enhances our comprehension of triangle geometry.
Circumradius Calculation
The circumradius is the radius of the circumscribed circle that passes through all three vertices of a triangle. The formula to calculate the circumradius (R) using the semi-perimeter (s) is given by:
R = (abc) / (4√[s(s - a)(s - b)(s - c)])
- a, b, c are the lengths of the sides of the triangle.
- s is the semi-perimeter, calculated as (a+b+c)/2.
- This formula is derived from the relationship between the sides of the triangle and its circumscribed circle.
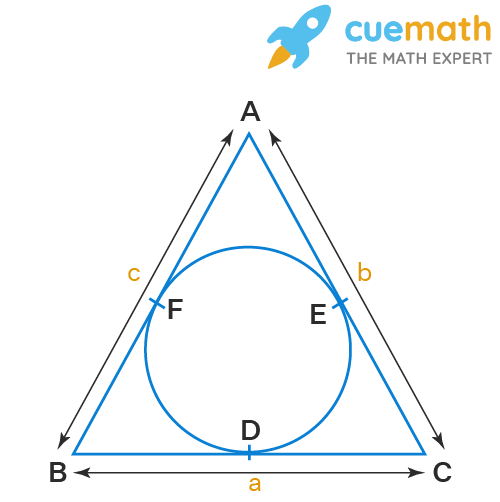
Inradius Calculation
The inradius is the radius of the inscribed circle that touches all three sides of the triangle. The formula to find the inradius (r) using the semi-perimeter is:
r = √[(s - a)(s - b)(s - c) / s]
- Here, a, b, c are the side lengths, and s is the semi-perimeter.
- The inradius can also be calculated using the area (A) of the triangle: r = A / s.
- This reflects the intimate relationship between the triangle\"s area and its semi-perimeter.
Practical Examples
- Example 1: For a triangle with sides 5, 12, and 13 units, first find the semi-perimeter and then use it to calculate the circumradius and inradius.
- Example 2: Analyze how changing one side length while keeping the semi-perimeter constant affects the circumradius and inradius.
Understanding the semi-perimeter\"s role in these calculations not only deepens our knowledge of geometry but also has practical applications in fields like engineering, architecture, and design.
_HOOK_
Triangle Area Calculation using Inradius and Semiperimeter (visual proof)
Discover the fascinating concept of the inradius in geometry! Watch this video to unravel the hidden secrets of the inradius and explore its connection to triangles and their properties.
Finding the Semi-perimeter of a Triangle: Formulas and Methods
Dive into the world of triangles with this captivating video! Learn about the different types of triangles, their angles, and how to find their areas and perimeters. Get ready to unlock the mysteries of triangles and revolutionize your understanding of geometry.
Examples and Solved Problems Involving Semi-Perimeter
The semi-perimeter of a triangle is a concept widely used in various geometric calculations. It is especially helpful in calculating the area of triangles using Heron\"s formula. Here, we present examples and solved problems to illustrate the application of the semi-perimeter in geometric problems.
Basic Calculation of Semi-Perimeter
To begin with, the semi-perimeter of a triangle is half of its perimeter. The formula for semi-perimeter is given by ( s = frac{a+b+c}{2} ), where ( a, b, ) and ( c ) are the lengths of the sides of the triangle.
Example 1: Semi-Perimeter of an Equilateral Triangle
Consider an equilateral triangle with each side measuring 16 units. The semi-perimeter in this case can be calculated as follows:
- Since all sides are equal, ( a = b = c = 16 ) units.
- Using the formula ( s = frac{a+b+c}{2} ), we get ( s = frac{16+16+16}{2} = 24 ) units.
Thus, the semi-perimeter of this equilateral triangle is 24 units.
Example 2: Semi-Perimeter in Heron\"s Formula
Heron\"s formula, which is used to calculate the area of a triangle, is an important application of the semi-perimeter. The formula is given by ( ext{Area} = sqrt{s(s-a)(s-b)(s-c)} ), where ( s ) is the semi-perimeter.
For a triangle with sides of lengths 6 units, 7 units, and 9 units, the semi-perimeter ( s ) can be calculated as ( s = frac{6+7+9}{2} = 11 ) units. The area can then be calculated using Heron\"s formula.
Example 3: Solving for Unknown Side Lengths
Consider an isosceles triangle with a semi-perimeter of 12 cm and the length of its unequal side being 10 cm. To find the length of each equal side:
- The formula for semi-perimeter in this case is ( s = a + frac{b}{2} ), where ( a ) is the length of the equal sides and ( b ) is the length of the unequal side.
- Given ( s = 12 ) cm and ( b = 10 ) cm, solving for ( a ) gives ( a = 7 ) cm.
Therefore, each equal side of the isosceles triangle is 7 cm long.
These examples demonstrate the versatility and usefulness of the semi-perimeter in solving various types of geometric problems. From finding the area of triangles using Heron\"s formula to solving for unknown side lengths, the semi-perimeter is a fundamental concept in geometry.

Extension to Quadrilaterals and Higher Polygons
The concept of semi-perimeter, primarily applied in the context of triangles, extends elegantly to quadrilaterals and other higher polygons. For quadrilaterals, the semi-perimeter is defined as half the sum of its four sides. This is expressed mathematically as ( s = frac{a + b + c + d}{2} ), where ( a, b, c, ) and ( d ) are the lengths of the sides of the quadrilateral.
In the realm of quadrilaterals, the semi-perimeter finds application in various area calculation formulas. For example, in tangential quadrilaterals, which possess an incircle, the area can be expressed as the product of the inradius and the semi-perimeter, aligning with the formula ( K = rs ). Moreover, for cyclic quadrilaterals, the area can be calculated using a formula akin to Heron\"s formula for triangles, expressed as ( K = sqrt{(s-a)(s-b)(s-c)(s-d)} ), where ( s ) is the semi-perimeter and ( a, b, c, ) and ( d ) are the side lengths.
Further generalizations are seen in Bretschneider\"s formula, which extends to all convex quadrilaterals. This formula incorporates the semi-perimeter and involves the calculation of the area using the formula ( K = sqrt{(s-a)(s-b)(s-c)(s-d) - abcd cdot cos^2(frac{alpha + gamma}{2})} ), where ( alpha ) and ( gamma ) are two opposite angles of the quadrilateral.
When considering regular polygons, the semi-perimeter\"s utility is also evident. The area of a convex regular polygon is the product of its semi-perimeter and its apothem. This highlights the semi-perimeter\"s role in simplifying complex geometric calculations across various shapes and forms.
Additionally, the concept scales up to encompass polygons with more than four sides, with the semi-perimeter being half the sum of all side lengths. This extension is critical in deriving and simplifying formulas in advanced geometry and polygonal calculations, demonstrating the semi-perimeter\"s versatility and importance in the field of geometry.
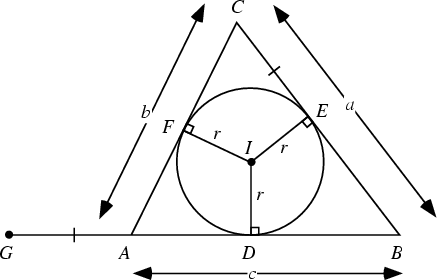
Relevance in Advanced Geometry and Trigonometry
The semi-perimeter of a polygon, especially in triangles, plays a crucial role in advanced geometry and trigonometry. It is not only fundamental in calculating the area of triangles using Heron\"s formula but also in deriving several trigonometric identities and theorems.
In trigonometry, the semi-perimeter is used to derive the half-angle formulas. These formulas are essential in expressing the sines, cosines, and tangents of half-angles of a triangle in terms of its semi-perimeter and sides. For instance, the sine of half the angle ( A ) in a triangle can be expressed as ( sin{frac{A}{2}} = sqrt{frac{(s-b)(s-c)}{bc}} ), where ( s ) is the semi-perimeter and ( b, c ) are the sides of the triangle.
These half-angle formulas are not only important for theoretical mathematics but also have practical applications in various fields such as engineering and physics. They provide a method to calculate angles and distances in situations where direct measurement is not possible.
In advanced geometry, the concept of the semi-perimeter is extended to derive various area formulas. Heron\"s formula, for example, uses the semi-perimeter to find the area of a triangle, given by ( A = sqrt{s(s-a)(s-b)(s-c)} ). This formula is particularly useful in situations where the height of the triangle is unknown or difficult to measure.
Furthermore, the semi-perimeter is used in more complex geometric problems, such as finding the areas of quadrilaterals and cyclic polygons. It forms the basis of several other geometric theorems and formulas, making it a cornerstone concept in the field of geometry and trigonometry.
In conclusion, the semi-perimeter is not just a simple geometric concept but a powerful tool in advanced mathematical calculations, providing a bridge between geometry and trigonometry, and aiding in the solving of complex problems in these and other related fields.

Practical Applications in Engineering and Design
The semi-perimeter, a fundamental concept in geometry, finds numerous practical applications in the fields of engineering and design. This measure, which is half the perimeter of a polygon, is crucial in various engineering calculations and designs.
In civil engineering and architecture, the semi-perimeter is used in designing structures and determining material requirements. For instance, Heron\"s formula, which involves the semi-perimeter, is used to calculate the area of irregularly shaped plots or land parcels. This is vital in resource allocation and estimation in construction projects.
In mechanical engineering, the concept of the semi-perimeter is applied in the design of mechanical parts and systems. For example, understanding the properties of shapes, including their semi-perimeters, is essential in the design and manufacture of components that need to fit together precisely.
In the design of aerodynamic structures, such as wings and fuselages, the semi-perimeter plays a role in calculating cross-sectional areas and understanding airflow dynamics. This is crucial in optimizing the design for efficiency and performance.
In environmental engineering, the semi-perimeter is used in hydrology for designing water flow systems, such as canals and drainage systems. Accurate calculations of areas and volumes, which often involve the semi-perimeter, are critical in these applications.
Furthermore, in computer-aided design (CAD) and 3D modeling, the semi-perimeter is used in algorithms that calculate areas and volumes, aiding in the accurate rendering and analysis of complex shapes and structures.
In summary, the semi-perimeter is not only a theoretical concept but also a practical tool in engineering and design, providing a foundation for calculations, estimations, and optimizations across various disciplines.

READ MORE:
Frequently Asked Questions About Semi-Perimeter
- What is the Semi Perimeter of a Triangle?
- The semi-perimeter of a triangle is half the perimeter of the triangle. It\"s calculated by adding the lengths of all three sides of the triangle and then dividing the sum by two.
- How to Find the Semi Perimeter of a Triangle?
- To find the semi-perimeter of a triangle, sum the lengths of all its sides and then divide by two. The formula is ( ext{Semi Perimeter} = frac{a + b + c}{2} ), where ( a, b, ) and ( c ) are the sides of the triangle.
- Where is the Semi Perimeter of Triangle Used?
- The semi-perimeter is used in Heron\"s formula to calculate the area of triangles when the lengths of all three sides are known. The formula is ( sqrt{s(s-a)(s-b)(s-c)} ), where ( s ) is the semi-perimeter, and ( a, b, ) and ( c ) are the sides.
- What is the Formula of the Semi Perimeter of Triangle?
- The formula for the semi-perimeter of a triangle is ( s = frac{a + b + c}{2} ), where ( a, b, ) and ( c ) are the three sides of the triangle.
- What is the Semi Perimeter of Triangle with Sides 40 cm, 24 cm, 32 cm?
- For a triangle with sides 40 cm, 24 cm, and 32 cm, the semi-perimeter is calculated using the formula ( s = frac{40 + 24 + 32}{2} ) which equals 48 cm.
- Find the Semi Perimeter of a Triangle if the Sides are 12 units, 22 units, and 15 units.
- For a triangle with sides 12 units, 22 units, and 15 units, the semi-perimeter is ( s = frac{12 + 22 + 15}{2} ) which equals 24.5 units.
Exploring the semi-perimeter reveals its crucial role in geometry, from simplifying complex calculations in triangles to broader applications in engineering, design, and advanced mathematics. This in-depth exploration offers valuable insights, making it an indispensable guide for enthusiasts and professionals alike.

_HOOK_