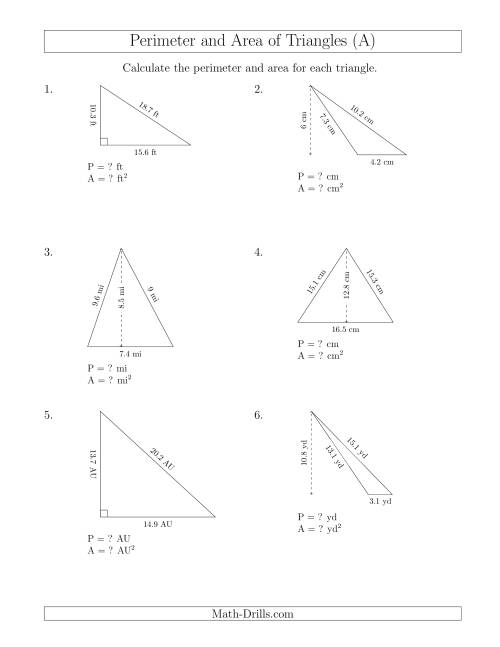
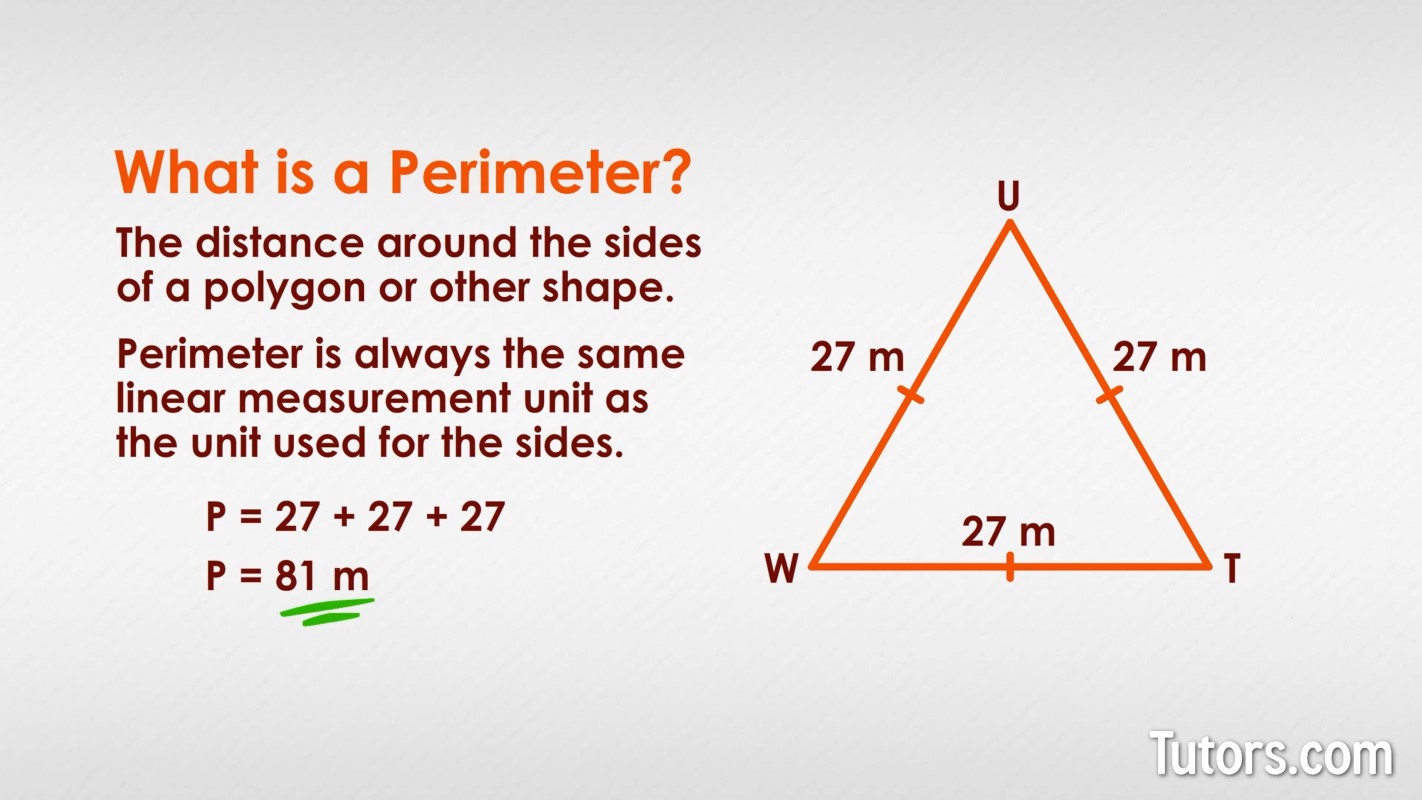
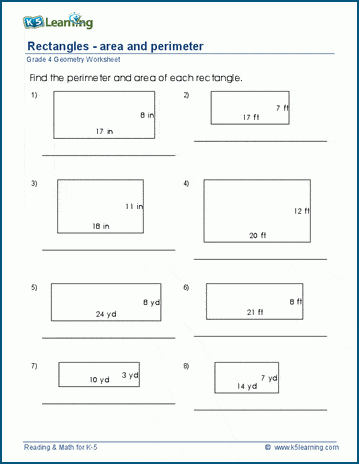
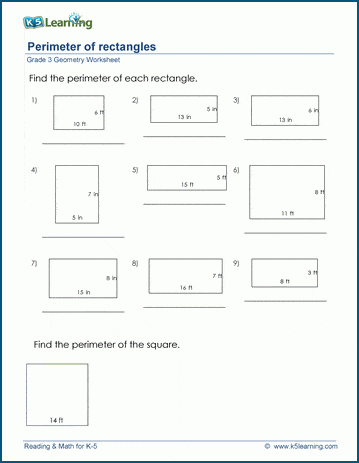
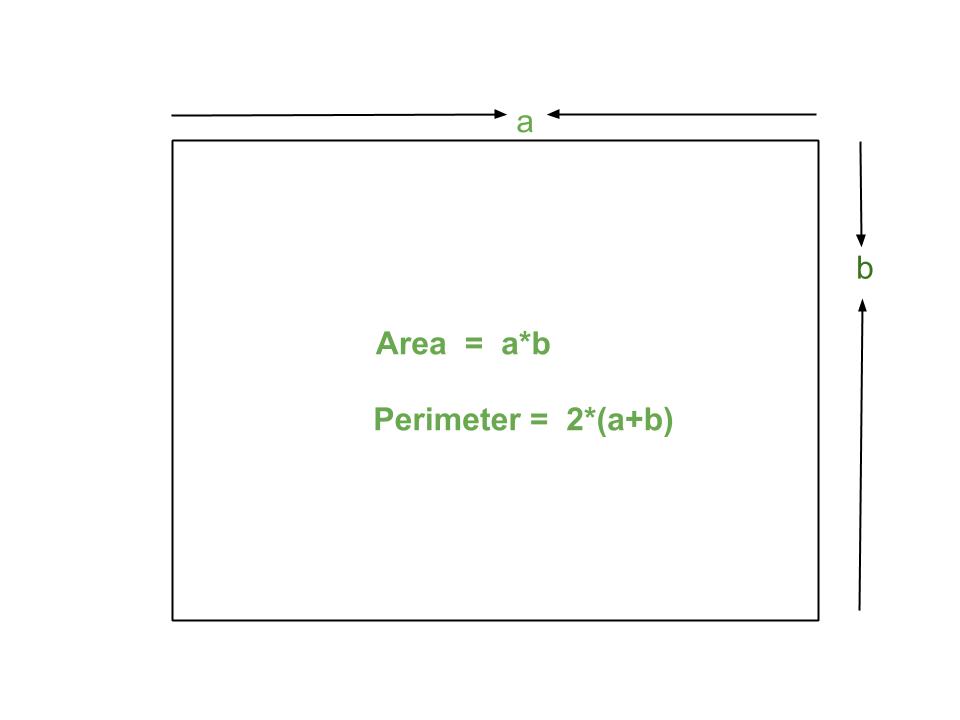
Topic area of perimeter of triangle: Discover the fascinating world of triangles, where mastering the area and perimeter unlocks a universe of geometric understanding and practical application.
Table of Content
- What is the formula for finding the area and perimeter of a triangle?
- Introduction to Triangle Geometry
- Basic Formulas for Triangle Area and Perimeter
- Special Cases: Equilateral, Isosceles, and Scalene Triangles
- Application of Heron\"s Formula for Irregular Triangles
- Triangle Inequality Theorem and Its Implications
- YOUTUBE: Area & Perimeter of a Triangle
- Calculating Triangle Area and Perimeter in Real-World Contexts
- Advanced Concepts: Incircle and Circumcircle of Triangles
- Understanding Triangles in Coordinate Geometry
- Interactive Examples and Problem-Solving Strategies
- Additional Resources and Learning Tools
What is the formula for finding the area and perimeter of a triangle?
The formula for finding the area of a triangle is:
A = (base * height) / 2
The formula for finding the perimeter of a triangle is:
P = side1 + side2 + side3
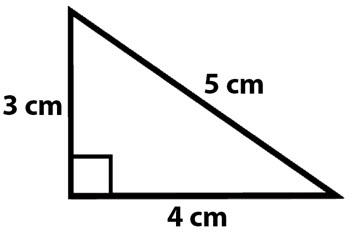
- To find the area of a triangle, you need to know the length of the base and the height of the triangle. Multiply the base by the height and then divide the result by 2.
- To find the perimeter of a triangle, you need to know the lengths of all three sides. Simply add up the lengths of all three sides.
It is important to note that the base of the triangle should be perpendicular to the height in order to accurately calculate the area. The sides of the triangle can have any length, but it\'s essential to include all three sides when calculating the perimeter.
READ MORE:
Introduction to Triangle Geometry
Triangles, with their three sides and angles, form a fundamental shape in geometry. This section introduces the basics of triangle geometry, essential for understanding concepts like area and perimeter.
- Definition: A triangle is a three-sided polygon, the simplest form of polygons, characterized by three edges and three vertices.
- Types of Triangles: Based on side lengths, triangles can be equilateral (all sides equal), isosceles (two sides equal), or scalene (no sides equal). Based on angle measurements, they can be acute, right-angled, or obtuse.
- Area and Perimeter: The area of a triangle is the region enclosed by its sides, while the perimeter is the total length of its sides. These measurements are crucial in various fields, from architecture to engineering.
- Formulas: The area is generally calculated as 0.5 x base x height. The perimeter is the sum of all sides. Special formulas like Heron\"s formula are used for specific triangle types.
- Applications: Understanding triangle geometry is vital in real-life applications, including construction, design, and even in the study of molecular structures.
This section sets the foundation for deeper exploration into the intricate world of triangles, their properties, and their significance in both theoretical and practical realms.

Basic Formulas for Triangle Area and Perimeter
Understanding the basic formulas for calculating the area and perimeter of a triangle is fundamental in geometry. Here are the key formulas:
- Area of a Triangle: The area (A) can be calculated as A = 0.5 × base (b) × height (h).
- Perimeter of a Triangle: The perimeter (P) is the sum of its three sides, P = a + b + c.
These formulas apply to various triangle types:
- Equilateral Triangle: With all sides equal (a), the area is A = (√3/4) × a², and the perimeter is P = 3a.
- Isosceles Triangle: Having two equal sides (a) and a base (b), the area is A = b/4 × √(4a² - b²).
- Scalene Triangle: With no equal sides, apply Heron\"s formula: A = √[s(s-a)(s-b)(s-c)], where s is the semi-perimeter.
These foundational formulas are not only vital for academic purposes but also have practical applications in fields such as architecture, engineering, and design.
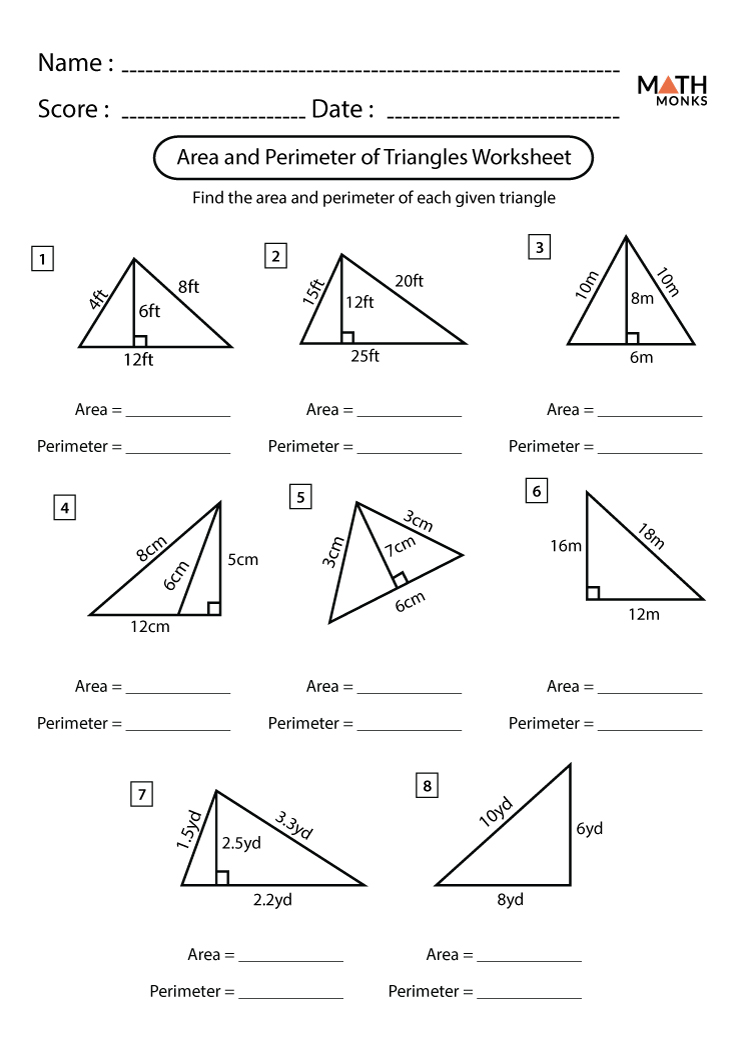
Special Cases: Equilateral, Isosceles, and Scalene Triangles
Triangles come in various forms, each with unique properties. This section delves into the special cases of equilateral, isosceles, and scalene triangles.
- Equilateral Triangles: In these triangles, all three sides and angles are equal. The angles are always 60°, making it a perfect example of symmetry in geometry. They are used in various applications due to their balanced properties.
- Isosceles Triangles: These have two sides of equal length and two angles of equal measure. This symmetry offers a simpler calculation for area and perimeter and plays a crucial role in architectural designs and structures.
- Scalene Triangles: With no equal sides or angles, scalene triangles are the most general form. They are a great example of triangles that often require the use of advanced formulas like Heron\"s formula for area calculation.
Understanding these special cases provides a deeper insight into triangle geometry and aids in solving complex geometric problems.

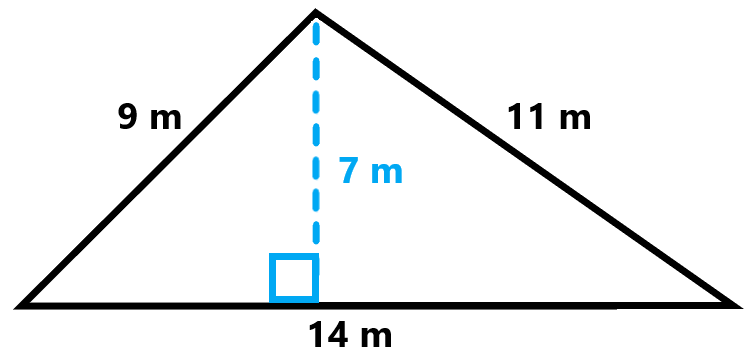
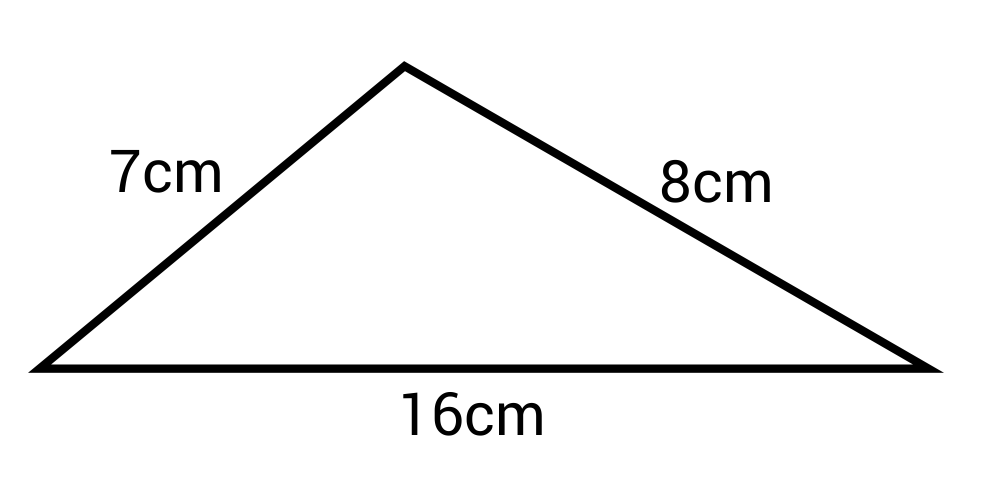
Application of Heron\"s Formula for Irregular Triangles
Heron\"s Formula is a powerful tool for calculating the area of irregular triangles, where traditional methods might not be straightforward. Here\"s how it\"s applied:
- Calculating Semi-Perimeter: First, find the semi-perimeter (s) of the triangle. It\"s half the sum of all three sides: s = (a + b + c) / 2.
- Applying the Formula: The area (A) can then be calculated using the formula: A = √[s(s - a)(s - b)(s - c)], where a, b, and c are the lengths of the sides.
- Real-World Applications: This formula is particularly useful in various fields such as architecture, surveying, and astronomy, where precise area calculations of irregular shapes are necessary.
Understanding and applying Heron\"s Formula not only simplifies complex geometric problems but also deepens our appreciation for the elegance of mathematical solutions.
_HOOK_
Triangle Inequality Theorem and Its Implications
The Triangle Inequality Theorem is a fundamental principle in geometry, stating that in any triangle, the sum of the lengths of any two sides must be greater than the length of the remaining side. This theorem has significant implications in various fields.
- Understanding Triangle Formation: This theorem helps in determining whether a set of three lines can form a triangle. If the sum of any two sides is not greater than the third side, a triangle cannot exist.
- Implications in Design and Construction: In architecture and construction, this theorem ensures the feasibility and stability of triangular structures and frameworks.
- Application in Mathematics and Physics: The theorem is crucial in advanced mathematical theories and physics, especially in studying the properties of space and shapes.
Overall, the Triangle Inequality Theorem plays a crucial role in both theoretical and practical aspects of geometry, offering essential insights into the nature of triangles and their applications.

Area & Perimeter of a Triangle
\"Discover the fascinating world of triangles in our latest video! Unlock the secrets of this versatile shape as we explore its properties, applications, and mind-bending mathematical mysteries. Get ready for an exhilarating journey into the captivating realm of triangles!\"
Area and Perimeter of Triangles
\"Calling all geometry enthusiasts! Join us as we dive into the labyrinth of triangles in our exciting new video. From equilateral to isosceles, obtuse to right-angled, we unravel the enchanting variety of triangles and their profound influence in art, architecture, and nature. Prepare for an epic exploration of the mesmerizing world of triangles!\"
Calculating Triangle Area and Perimeter in Real-World Contexts
The Triangle Inequality Theorem is a fundamental principle in geometry, stating that in any triangle, the sum of the lengths of any two sides must be greater than the length of the remaining side. This theorem has significant implications in various fields.
- Understanding Triangle Formation: This theorem helps in determining whether a set of three lines can form a triangle. If the sum of any two sides is not greater than the third side, a triangle cannot exist.
- Implications in Design and Construction: In architecture and construction, this theorem ensures the feasibility and stability of triangular structures and frameworks.
- Application in Mathematics and Physics: The theorem is crucial in advanced mathematical theories and physics, especially in studying the properties of space and shapes.
Overall, the Triangle Inequality Theorem plays a crucial role in both theoretical and practical aspects of geometry, offering essential insights into the nature of triangles and their applications.

Advanced Concepts: Incircle and Circumcircle of Triangles
The Triangle Inequality Theorem is a fundamental principle in geometry, stating that in any triangle, the sum of the lengths of any two sides must be greater than the length of the remaining side. This theorem has significant implications in various fields.
- Understanding Triangle Formation: This theorem helps in determining whether a set of three lines can form a triangle. If the sum of any two sides is not greater than the third side, a triangle cannot exist.
- Implications in Design and Construction: In architecture and construction, this theorem ensures the feasibility and stability of triangular structures and frameworks.
- Application in Mathematics and Physics: The theorem is crucial in advanced mathematical theories and physics, especially in studying the properties of space and shapes.
Overall, the Triangle Inequality Theorem plays a crucial role in both theoretical and practical aspects of geometry, offering essential insights into the nature of triangles and their applications.
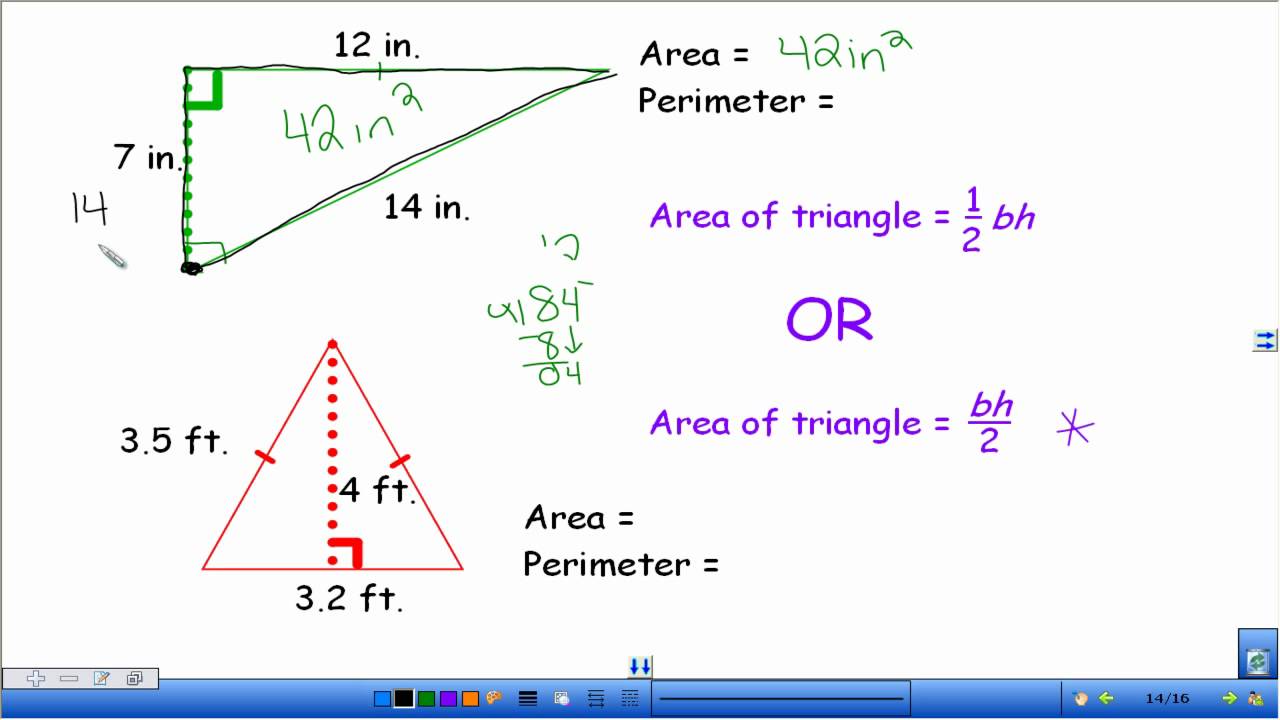
Understanding Triangles in Coordinate Geometry
Understanding the area of triangles in coordinate geometry involves applying specific formulas that use the coordinates of the triangle\"s vertices. This approach is key in computational and graphical applications of geometry.
Area Calculation Methods
- Basic Formula: For a triangle with vertices A, B, and C at coordinates (x₁, y₁), (x₂, y₂), and (x₃, y₃), the area is calculated as:
- A = 1/2 |x₁(y₂ − y₃) + x₂(y₃ − y₁) + x₃(y₁ − y₂)|
- Determinant Method: This involves a matrix representation:
- A = 1/2 |det[x₁ y₁ 1; x₂ y₂ 1; x₃ y₃ 1]|
- Here, \"det\" refers to the determinant of the matrix formed by the vertices\" coordinates.
- Heron\"s Formula: After calculating the lengths of the sides using the distance formula, Heron\"s formula can be applied to find the area.
Special Cases
- If the calculated area is zero, it indicates that the points are collinear, meaning they lie on a straight line and do not form a triangle.
- The \"handedness\" of the points can be inferred from the sign of the area calculated without the absolute value. A negative value suggests a certain orientation of the points.
Practical Applications
These methods are crucial in various fields, including computer graphics, architectural design, and geographical mapping, where triangle areas need to be calculated based on spatial coordinates.
Interactive Exploration
Using software tools or programming libraries that support coordinate geometry, one can visualize and manipulate triangle vertices in a coordinate plane, offering a deeper understanding of these concepts.
Interactive Examples and Problem-Solving Strategies
This section provides interactive examples and strategies to understand and solve problems related to the area and perimeter of triangles. Engaging in these activities enhances understanding and application of geometric concepts.
Interactive Activities
- Counting Unit Squares: Students can practice finding area by counting unit squares in various shapes, including triangles.
- Creating Shapes: An interactive exercise where students create rectangles or other shapes with a given area, helping them understand the relationship between shape dimensions and area.
- Perimeter Exploration: Activities to find the perimeter by counting units or using given side lengths, reinforcing the concept of perimeter in different shapes.
Problem-Solving Strategies
- Understanding Formulas: Learning and applying formulas for the area and perimeter of triangles, including special cases like equilateral and right-angled triangles.
- Missing Dimensions: Solving problems that involve finding a missing side length when given the area or perimeter of a triangle, which helps in understanding the inverse relationship between area and dimensions.
- Grid-Based Problems: Using grids to calculate the area of triangles and other shapes, which aids in visualizing and solving geometry problems.
Challenges and Quizzes
Engage in quizzes and challenges that test understanding of area and perimeter concepts. These activities help identify areas of growth and reinforce learning through practical application.
Real-World Application
Encouraging the application of these concepts in real-world scenarios, like calculating the area of land plots or designing objects with specific dimensions, to show the practical importance of understanding area and perimeter.
_HOOK_
READ MORE:
Additional Resources and Learning Tools
Exploring the concepts of triangle area and perimeter can be greatly enhanced through various online resources and tools. These materials provide comprehensive learning experiences, from basic principles to advanced applications.