Perimeter of Ellipse Formula: Unveiling the Mysteries of Elliptical Calculations

The formula for finding the perimeter of an ellipse is not as straightforward as the formula for finding the area.

However, there are several approximations that can be used to estimate the perimeter of an ellipse:

1. The most common approximation is to use the Ramanujan approximation formula:

P ≈ π(a + b) * (1 + (3h / (10 + √(4 - 3h))))

• P is the perimeter
• π is a mathematical constant approximately equal to 3.14159
• a is the length of the major axis
• b is the length of the minor axis
• h is the square of the difference between a and b, divided by the square of the sum of a and b (h = (a - b)^2 / (a + b)^2)
2. Another common approximation is to use the Ramanujan second approximation formula:

P ≈ π(a + b) * (1 + (h / 4))

3. There are also other approximation formulas available, such as those derived by Ritz, Varga, and Archimedes.

These formulas provide reasonably accurate estimations of the perimeter of an ellipse, but it\'s important to note that they are approximations and may not be as precise as desired for certain applications.

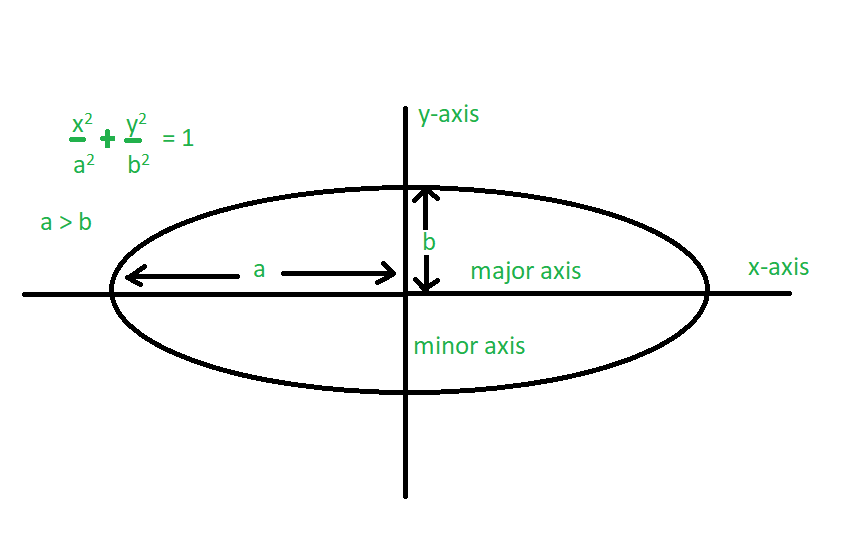
An ellipse, a fundamental shape in geometry and physics, is defined as the locus of points in a plane where the sum of distances from two fixed points (foci) is constant. This unique property leads to its oval shape. The ellipse was first studied by ancient mathematicians like Menaechmus and Euclid, and it was named by Apollonius. It\"s one of the conic sections, formed by intersecting a plane with a cone at an angle. Notably, a circle is a special case of an ellipse where the two foci coincide.

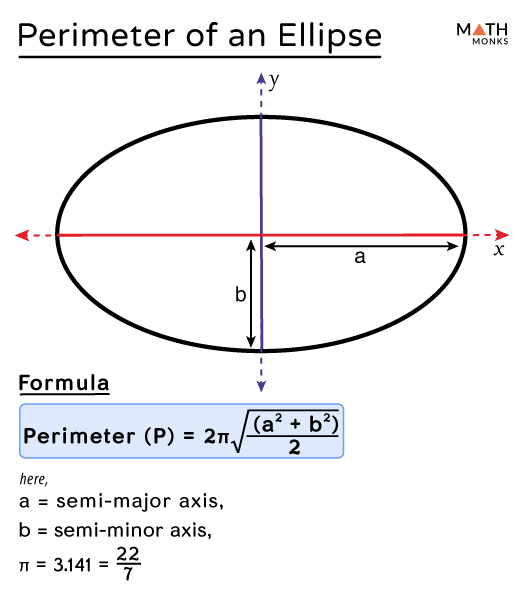
The ellipse is characterized by its major and minor axes. The major axis is the longest diameter, running through the center at the widest part of the ellipse, while the minor axis is the shortest, at the narrowest part. Each axis is divided into two equal parts: the semi-major and semi-minor axes. The sum of distances from any point on the ellipse to the two foci remains constant, equal to the length of the major axis. The eccentricity of an ellipse, a measure of its deviation from a circular shape, is always between zero and one.

Ellipses have various real-world applications, including in astronomy where planetary orbits are elliptical with the sun at one focus, and in engineering and design for creating oval shapes. Understanding the properties of ellipses, such as their axes, foci, and eccentricity, is crucial for calculating their area and perimeter, with the latter being notably complex due to its approximation nature.

Several methods exist for calculating the perimeter of an ellipse, including Ramanujan\"s approximation and integral-based formulas. These calculations involve complex mathematical concepts like infinite series and integration, demonstrating the intricacy of accurately determining the perimeter of an ellipse.

The perimeter of an ellipse, a fundamental geometric shape, represents the total distance around its edge. Unlike a circle, calculating the perimeter of an ellipse is complex and cannot be done with a simple formula. This complexity arises due to the elliptical shape, which involves two axes of different lengths – the major and minor axes.

One basic approach to approximate the perimeter involves using the semi-major and semi-minor axes (denoted as \"a\" and \"b\", respectively). A simple yet less accurate formula for the perimeter is P ≈ π(a + b). However, for more accurate approximations, various complex formulas are used, including those derived by Ramanujan and other mathematical approaches involving infinite series and integral calculus.

Ramanujan\"s first approximation formula for the perimeter is given as P ≈ π(a+b) [1 + 3h/(10 + √(4-3h))], where h = (a-b)²/(a+b)². For ellipses with low eccentricity, this formula provides a close approximation. The eccentricity \"e\" of an ellipse is a measure of its deviation from being circular and is calculated using the formula e = √(1 - (b²/a²)).

For more precise calculations, especially for ellipses with high eccentricity, integral calculus is used. The integral formula for the perimeter of an ellipse is P = 4a ∫(0 to π/2) √(1 - e² sin² θ) dθ, where \"e\" is the eccentricity. This integral, known as the complete elliptic integral of the second kind, is more complex but provides exact results.

Understanding the basic concept of ellipse perimeter involves recognizing the complexities involved in its calculation and the various mathematical methods employed to approximate or accurately determine it. The ellipse\"s unique shape, defined by its major and minor axes and eccentricity, makes the task challenging yet intriguing for mathematicians and scientists alike.

The perimeter of an ellipse, intriguingly complex, lacks a straightforward formula akin to that of a circle. Instead, multiple approximations and integral-based formulas are used, each varying in complexity and accuracy.

One of the simplest approximations uses the semi-major (a) and semi-minor (b) axes, giving a perimeter estimate of P ≈ π(a + b). This formula is generally effective for ellipses with minor eccentricities.

For more precise calculations, especially for ellipses with higher eccentricity, more complex formulas are employed. One of the renowned formulas is Ramanujan\"s approximation, which provides a close estimation for the ellipse perimeter. Ramanujan\"s first approximation formula is expressed as P ≈ π(a+b) [1 + 3h/(10 + √(4-3h))], where h = (a-b)²/(a+b)².

Another approach involves using infinite series. The infinite series formula, though complex, expands to offer a closer approximation of the perimeter. It involves calculating terms to an infinite degree, with each additional term providing a finer approximation.

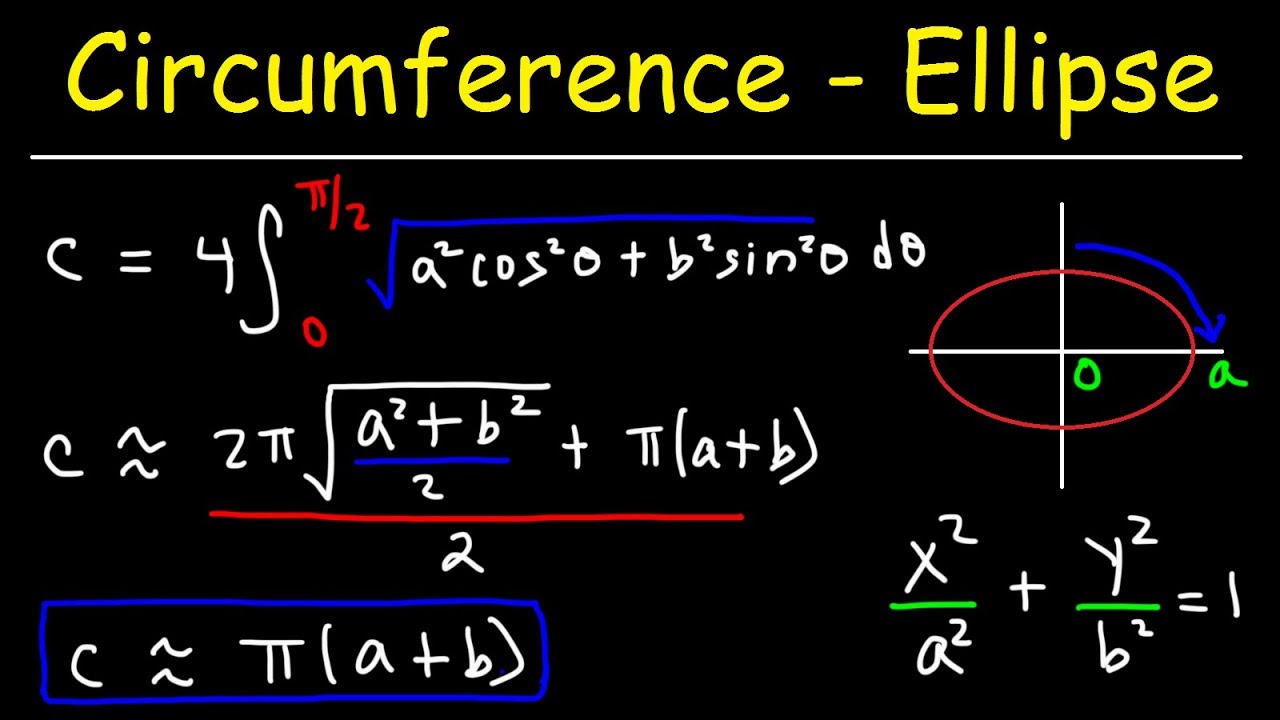
An exact solution for the ellipse perimeter can be obtained through integration. The integral formula is P = 4a ∫(0 to π/2) √(1 - e² sin² θ) dθ, where e is the eccentricity of the ellipse. This formula, known as the complete elliptic integral of the second kind, is complex but provides precise results.

The choice of formula depends on the required accuracy and the elliptical properties, particularly the eccentricity. Understanding these formulas provides a deep insight into the nature of ellipses and their geometric properties.

Srinivasa Ramanujan, a renowned mathematician, developed several approximations for calculating the perimeter of an ellipse, which are known for their simplicity and high accuracy.

The first approximation formula provided by Ramanujan is expressed as:

• P ≈ π [ 3(a + b) - √ [ (3a + b)(a + 3b) ] ]

This formula is effective for ellipses with minor eccentricities and offers a close approximation to the actual perimeter.

Ramanujan\"s second approximation is even more refined, especially for ellipses with greater eccentricities. It is given as:

• P ≈ π(a+b) [ 1 + 3h/(10 + √(4-3h)) ]

Here, h is defined as (a-b)²/(a+b)². This formula is known for its remarkable accuracy, especially for ellipses that are not significantly elongated.

For ellipses with very low eccentricity, the perimeter can also be approximated by simpler formulas like P ≈ π(a + b), which, although less accurate, provides a reasonable estimate for nearly circular ellipses.

These approximations by Ramanujan are significant because they offer a practical way to calculate the perimeter of an ellipse without resorting to complex integral calculus, making them highly valuable in both academic and applied settings.

Calculating the perimeter of an ellipse involves complex mathematical techniques, particularly integrals and infinite series. Unlike simpler geometric shapes, the ellipse\"s perimeter calculation cannot be expressed by a straightforward formula.

The integral formula for the perimeter of an ellipse is derived using the concept of eccentricity \"e\", where e = √(a² - b²)/a. This formula is represented as:

• P = 4a ∫ (from 0 to π/2) √(1 - e² sin² θ) dθ

This integral, known as the complete elliptic integral of the second kind, provides an exact solution for the ellipse\"s perimeter. However, its calculation involves an infinite series, making it complex and challenging to compute.

In addition to the integral approach, there are infinite series formulas used to approximate the ellipse\"s perimeter. One such method involves expanding the series to numerous terms, each adding to the accuracy of the approximation. For instance, one formula expands as follows:

• Ellipse perimeter approx = 2a π [ 1 - (1/2)² e² - (1x3/2x4)² e⁴ /3 - ...]

These series continue infinitely, and the more terms calculated, the closer the approximation gets to the actual perimeter. However, despite their accuracy, these methods are complex and require substantial computational effort.

The complexity of these formulas reflects the intricate nature of elliptical shapes, differentiating them from simpler geometrical figures like circles or squares.

The eccentricity of an ellipse plays a crucial role in determining its shape and the complexity of calculating its perimeter. Eccentricity (e) is a measure of how much an ellipse deviates from being circular, with values ranging from 0 (a perfect circle) to values close to 1 (highly elongated ellipses).

Low Eccentricity Ellipses: When an ellipse has low eccentricity (close to 0), it resembles a circle. In these cases, the perimeter can be approximated more accurately by simpler formulas. For example, for an ellipse that is almost circular (where a and b are nearly equal), the perimeter can be approximated by P ≈ π(a + b).

High Eccentricity Ellipses: For ellipses with high eccentricity (close to 1), the shape becomes highly elongated. These ellipses are challenging to deal with as the conventional approximation formulas become less accurate. In such cases, more complex formulas or integral-based calculations are often required to approximate the perimeter accurately. The complete elliptic integral of the second kind, given by P = 4a ∫(0 to π/2) √(1 - e² sin² θ) dθ, can provide an exact solution but requires intricate calculations involving an infinite series.

In summary, the eccentricity of an ellipse significantly influences the method and accuracy of calculating its perimeter. While simpler formulas suffice for ellipses with low eccentricity, highly eccentric ellipses demand more complex mathematical approaches.

Ellipses, fascinating geometric shapes, are not just theoretical constructs but have several practical applications and appear in various real-life scenarios. The unique properties of ellipses make them useful in a wide range of fields, from astronomy to engineering.

Astronomy and Space Science

• Planetary Orbits: Ellipses describe the orbits of planets around the sun. This concept, first proposed by Johannes Kepler, indicates that planets move in elliptical orbits with the sun at one focal point.
• Satellite Trajectories: The paths of satellites around Earth or any other celestial body are often elliptical, with varying eccentricities based on their launch parameters and intended function.

Engineering and Technology

• Antenna Design: In the field of telecommunications, the shape of elliptical antennas helps in focusing signals, thereby enhancing communication quality and reducing interference.
• Optical Instruments: Ellipses are used in the design of optical instruments like telescopes and cameras, where mirrors with elliptical shapes help in focusing light effectively.

Architecture and Art

• Acoustic Design: The elliptical shape is used in the design of auditoriums and concert halls to optimize sound distribution and enhance acoustic quality.
• Artistic Perspective: Ellipses are used in art and graphic design to create perspectives and illusions of depth, especially in depicting circular objects in a three-dimensional view.

Everyday Applications

• Industrial Design: Many machine parts and tools are designed with elliptical shapes to provide specific mechanical advantages or to fit particular spaces efficiently.
• Sports: In sports, the trajectory of balls in certain games, like tennis or table tennis, can form elliptical paths depending on how they are hit.

Mathematics and Physics

• Statistical Data Representation: Ellipses are used in statistics, particularly in the form of confidence ellipses, to represent and interpret multivariate data visually.
• Theoretical Physics: In physics, the concept of elliptical orbits is crucial in understanding celestial mechanics and the gravitational interactions between astronomical bodies.

These examples illustrate how the ellipse, from its mathematical properties to its unique shape, plays a vital role in various domains, blending the beauty of mathematics with the practicality of its applications.

Calculating the perimeter of an ellipse has been a subject of mathematical inquiry for centuries, leading to the development of various formulas. Each formula offers a different level of accuracy and complexity. This comparative analysis explores some of the most significant formulas.

Simple Approximations

1. Basic Approximation: One of the simplest formulas is (P approx pi(a+b)), providing a rough estimate for ellipses that are not too elongated.
2. Ramanujan\"s First Approximation: Ramanujan proposed (P approx pi [ 3(a + b) - sqrt{(3a + b)(a + 3b)} ]), known for its balance between simplicity and accuracy, particularly for ellipses with low eccentricity.

Advanced Approximations

• Ramanujan\"s Second Approximation: Another formula by Ramanujan, (P approx pi (a+b) [ 1 + 3h/(10+sqrt{4-3h}) ]), where (h = (a-b)^2/(a+b)^2), is renowned for its precision up to the coefficient of (e^{18}) in its expansion.
• Integral Based Formulas: More complex formulas involve integrals and infinite series, such as (P = 4a int_{0}^{pi/2} sqrt{1-e^{2} sin^{2} heta} , d heta), offering high precision at the cost of computational complexity.

Comparison and Practicality

For practical purposes, the choice of formula depends on the required precision and the ellipse\"s properties. Simple formulas are adequate for most everyday applications, while advanced formulas are reserved for high-precision calculations in scientific and engineering contexts. Interestingly, all formulas converge to the same value for a circle (where (a = b)).

Calculating the exact perimeter of an ellipse presents unique challenges and limitations, primarily due to the complexity of its shape and the absence of a simple, closed-form formula.

Complexity of Exact Calculation

• The exact calculation of an ellipse\"s perimeter involves advanced mathematical functions, such as the complete elliptic integral of the second kind or the Gaussian hypergeometric function, which are typically covered in advanced mathematics courses.
• These exact formulas require the use of specialist mathematical software to calculate the perimeter to arbitrary precision.

Approximations and Limitations

1. Various approximation formulas exist, such as those proposed by Ramanujan, which provide a balance between computational simplicity and accuracy. However, these approximations have limitations, especially as the ellipse becomes more elongated.
2. For ellipses with low eccentricity, these approximations are quite accurate, but their accuracy diminishes for highly elongated ellipses.
3. The challenge lies in finding a formula that is both simple enough to be practical and accurate enough for a wide range of ellipse shapes.

Practical Considerations

In practical applications, the choice of formula for calculating the ellipse\"s perimeter is often a trade-off between the required precision and the computational resources available. For most real-world applications, approximation formulas suffice.

The ongoing exploration in the field of mathematics to find more accurate and simpler formulas for the ellipse\"s perimeter calculation continues to be a topic of research and intrigue.

When exploring advanced topics in ellipse perimeter calculations, mathematicians delve into a realm far beyond basic approximation formulas. These advanced methods often involve complex mathematical concepts and calculations.

Infinite Series in Ellipse Perimeter Calculation

• One advanced method involves the use of infinite series for calculating the ellipse\"s perimeter. This approach requires the calculation of numerous terms to achieve a close approximation of the perimeter.
• For example, an infinite sum formula involving a series of calculations using the binomial coefficient with half-integer factorials provides a more accurate result after a few terms are calculated.

Parametric Equations and Integral Calculations

1. Another advanced method utilizes parametric equations and integral calculations. This approach involves complex integrals to calculate the perimeter, especially when dealing with ellipses that exhibit significant eccentricity.
2. The integral formula, often seen in the form of (P = 4a int_{0}^{pi / 2} sqrt{1-e^{2} sin ^{2} heta} , dt), is one such example where \"e\" represents the eccentricity of the ellipse.

Geometrical Properties of Ellipses

Advanced studies also focus on the inherent geometrical properties of ellipses, such as their foci, eccentricity, and the behavior of lines parallel to the minor axis passing through the foci, known as latera recta.

These advanced topics showcase the intricate and complex nature of ellipse perimeter calculations, demonstrating the mathematical depth and precision required in such endeavours.

Calculating the perimeter of an ellipse can be complex, but interactive tools and calculators make it easier. Here are some methods and tools to understand and calculate the ellipse perimeter accurately.

1. Approximation Formulas:
2. Simple Approximation: P ≈ 2π √((a²+b²)/2) - This formula gives an approximation within about 5% of the true value for ellipses that are not excessively elongated.
3. Ramanujan\"s Approximation: P ≈ π [3(a+b) - √((3a+b)(a+3b))] - A more accurate approximation proposed by the famous mathematician Ramanujan.
4. Integral and Infinite Series:
5. Exact Integral Formula: P = 4a ∫ from 0 to π/2 √(1 - e² sin² θ) dθ - While this gives an exact value, it requires an infinite series of calculations, making it impractical for quick computations.
6. Online Calculators:
7. These calculators use various formulas, including the approximations and integral methods, to calculate the ellipse perimeter. Users can input the values of the major (a) and minor (b) axes to get an instant calculation of the perimeter.

These tools and formulas provide different levels of approximation and accuracy, allowing users to choose based on their needs and the specific requirements of their calculations.

The study of ellipses, particularly in the context of determining their perimeter, has been a subject of considerable mathematical interest and practical significance. Despite significant advancements, the exact calculation of an ellipse\"s perimeter remains elusive, primarily due to its reliance on complex integrals and series expansions. However, various approximation formulas have been developed to estimate the perimeter with varying degrees of accuracy.

Among the notable methods, Ramanujan\"s formulas stand out for their simplicity and precision. Ramanujan proposed two formulas that provide highly accurate estimates of an ellipse\"s perimeter, especially for ellipses with low eccentricity. These formulas have been foundational in the study of ellipses and continue to be widely used in both academic and practical applications.

One fundamental approach to calculating an ellipse\"s perimeter involves using parametric equations and arc length formulas. This method, though mathematically rigorous, can be complex and is more suited for theoretical studies. In contrast, simpler approximations, like the quadratic expression and the formulas involving eccentricity, offer a more accessible means for practical calculations, albeit with less precision.

Looking to the future, the field of ellipse research may benefit from exploring new computational methods and algorithms that can enhance the accuracy of perimeter calculations. The development of more sophisticated approximation formulas, possibly leveraging advancements in numerical analysis and computer-aided calculations, holds promise. Additionally, the exploration of ellipses in multidisciplinary contexts, such as astronomy, engineering, and computer graphics, may yield new insights and applications.

In summary, while the quest for an exact formula for the perimeter of an ellipse remains a challenging mathematical problem, the existing approximation methods offer valuable tools for both theoretical exploration and practical application. The ongoing research in this area is likely to continue uncovering deeper insights into the properties of ellipses and their applications in various fields.

Discovering the elusive perimeter of an ellipse unlocks a realm of mathematical beauty and practical application. Join us on a journey through elegant formulas and ingenious approximations that reveal the intricate tapestry of this classic geometric shape.