Topic perimeter of an isosceles trapezoid: Explore the intriguing world of geometry with our comprehensive guide on the "Perimeter of an Isosceles Trapezoid", unlocking a fascinating blend of mathematical elegance and practical application.
Table of Content
- How do you calculate the perimeter of an isosceles trapezoid?
- Basic Definition and Formula for Perimeter
- Calculating Perimeter with Given Sides
- Properties of Isosceles Trapezoids
- YOUTUBE: Finding the Area and Perimeter of an Isosceles Trapezoid
- Distinguishing Between Trapezoids and Isosceles Trapezoids
- Isosceles Trapezoid Diagonals and Their Properties
- Practical Examples and Problem Solving
- Role of Base Angles in Isosceles Trapezoids
- Understanding the Height of Isosceles Trapezoids
- Advanced Calculations: Area, Diagonals, and More
- Frequently Asked Questions About Isosceles Trapezoids
How do you calculate the perimeter of an isosceles trapezoid?
To calculate the perimeter of an isosceles trapezoid, you need to know the lengths of its bases and the height. Here are the steps to calculate the perimeter:
- Identify the lengths of the bases of the trapezoid.
- Measure the height of the trapezoid.
- Add the lengths of the bases of the trapezoid.
- Multiply the sum by 2 to account for the two non-parallel sides of the trapezoid.
- Add the height of the trapezoid to the sum of the bases multiplied by 2.
The formula to calculate the perimeter of an isosceles trapezoid can be summarized as follows:
Perimeter = (Base1 + Base2) * 2 + Height
By substituting the actual measurements into this formula, you can calculate the perimeter of the isosceles trapezoid.
READ MORE:
Basic Definition and Formula for Perimeter
An isosceles trapezoid is a fascinating geometric figure with one pair of parallel sides called bases and another pair of non-parallel, equal-length sides known as legs. Its unique shape plays a significant role in various mathematical and practical applications.
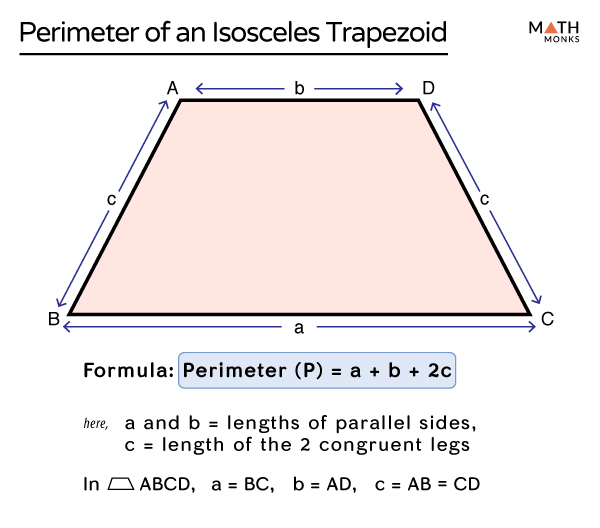
The formula to calculate the perimeter of an isosceles trapezoid is straightforward yet elegant. The perimeter (P) is the sum of the lengths of all its sides:
[P = a + b + 2c]
- (a) and (b) are the lengths of the parallel sides (bases).
- (c) is the length of the non-parallel, equal sides (legs).
This formula is a direct consequence of the trapezoid\"s symmetry, where the legs ((c)) are of equal length, simplifying the perimeter calculation. The concept becomes clearer with an example:
Example: For an isosceles trapezoid with bases (a = 10) inches, (b = 15) inches, and legs (c = 20) inches, the perimeter is calculated as:
[P = 10 + 15 + 2 imes 20 = 65] inches.
This example illustrates the simplicity and elegance of the perimeter formula for isosceles trapezoids, making it an accessible concept for learners at various levels.

Calculating Perimeter with Given Sides
Calculating the perimeter of an isosceles trapezoid is a straightforward process when you have the measurements of its sides. An isosceles trapezoid, characterized by its two parallel bases and two equal-length non-parallel sides, requires a simple formula for its perimeter.
The formula to calculate the perimeter (P) is:
[P = a + b + 2 imes c]
- Identify the lengths of the two parallel sides, labeled (a) and (b).
- Measure the length of one of the non-parallel sides (legs), labeled (c). Remember, in an isosceles trapezoid, both legs are of equal length.
- Add the lengths of the bases and twice the length of the leg to find the perimeter.
For example, if an isosceles trapezoid has bases of 10 cm and 15 cm, and the lengths of its non-parallel sides are both 5 cm, the perimeter is calculated as follows:
[P = 10 + 15 + 2 imes 5 = 35] cm
This simple approach allows for quick and accurate calculations, making it an essential skill for students and professionals working with geometric shapes.

Properties of Isosceles Trapezoids
The isosceles trapezoid is a unique and interesting geometric figure, exhibiting several distinctive properties that set it apart from other quadrilaterals. Understanding these properties is crucial for grasping the trapezoid\"s geometry and for solving related mathematical problems.
- Parallel Bases: The defining characteristic of an isosceles trapezoid is its two parallel sides known as bases.
- Congruent Non-parallel Sides: The non-parallel sides, or legs, of an isosceles trapezoid are congruent (equal in length).
- Congruent Base Angles: Each pair of base angles (angles adjacent to the same base) are congruent. This means if one base angle is 30°, the other angle adjacent to the same base will also be 30°.
- Congruent Diagonals: The diagonals of an isosceles trapezoid are congruent, meaning they are of equal length.
- Diagonal Properties: The diagonals divide each other proportionally, in a ratio equal to the ratio of the lengths of the parallel sides they intersect.
- Line of Symmetry: The isosceles trapezoid has a line of symmetry bisecting one pair of opposite sides, typically running through the midpoints of the bases.
- No Rotational Symmetry: Unlike some other geometric shapes, the isosceles trapezoid does not exhibit rotational symmetry, except in the special case where it is a rectangle.
- Sum of Opposite Angles: The sum of the measures of any two opposite angles in an isosceles trapezoid is 180 degrees.
- Median Length: The median (mid-segment) of an isosceles trapezoid, connecting the midpoints of the non-parallel sides, is parallel to the bases and its length equals half the sum of the base lengths.
These properties not only provide a deeper understanding of the isosceles trapezoid but also aid in solving complex geometric problems involving this shape.

Finding the Area and Perimeter of an Isosceles Trapezoid
Explore the captivating world of areas in this video! Learn how to calculate the area of various shapes and discover practical applications of this fundamental concept. It\'s time to unlock the secrets of areas and expand your mathematical knowledge!
Distinguishing Between Trapezoids and Isosceles Trapezoids
Understanding the differences between trapezoids and isosceles trapezoids is crucial for geometry enthusiasts and students alike. While both are four-sided figures, they have distinct characteristics that set them apart.
- Definition of a Trapezoid: A trapezoid is defined as a quadrilateral with only one pair of parallel sides. These parallel sides are known as the bases.
- Definition of an Isosceles Trapezoid: An isosceles trapezoid is a special type of trapezoid where the non-parallel sides (legs) are equal in length. This equality of legs leads to congruent base angles and diagonals. Additionally, an isosceles trapezoid has a line of symmetry bisecting one pair of opposite sides.
- Legs and Angles: In a regular trapezoid, the legs (non-parallel sides) may be of different lengths, and the base angles are not necessarily equal. Conversely, in an isosceles trapezoid, the legs are of equal length, and each pair of base angles are equal.
- Diagonals: In an isosceles trapezoid, the diagonals are congruent (equal in length). However, in a general trapezoid, the diagonals may not be congruent.
- Symmetry: An isosceles trapezoid typically exhibits reflection symmetry across a vertical axis, while a regular trapezoid does not necessarily have any symmetry.
These differences are key in identifying and working with these two distinct types of quadrilaterals in geometry.
_HOOK_
Perimeter of an Isosceles Trapezoid with One Angle and One Base Length
Ready to dive into the world of angles? This video will provide you with a comprehensive understanding of different types of angles, their properties, and how they relate to everyday life. Get ready to sharpen your geometry skills and uncover the hidden angles all around us!
Isosceles Trapezoid Diagonals and Their Properties
The diagonals of an isosceles trapezoid offer fascinating insights into its geometry. Understanding these diagonals is crucial for comprehending the trapezoid\"s structure and solving related problems.
- Equal Length Diagonals: One of the defining characteristics of an isosceles trapezoid is that its diagonals are of equal length. This property distinguishes it from other trapezoids where diagonals may not be congruent.
- Diagonals Divide Proportionally: The diagonals in an isosceles trapezoid not only have the same length but also divide each other into segments of equal length. This means if one diagonal is divided into two segments, the other diagonal is divided into two segments of the same lengths respectively.
- Diagonal Length Calculation: The length of each diagonal can be calculated using Ptolemy\"s theorem, which involves the lengths of the parallel sides and the legs. Specifically, the length of a diagonal is given by the square root of the product of the lengths of the parallel sides plus the square of the leg length.
- Diagonal Ratio: The ratio in which each diagonal is divided corresponds to the ratio of the lengths of the parallel sides that they intersect. This means the segment ratios of the diagonals are directly related to the lengths of the bases of the trapezoid.
These properties of the diagonals not only contribute to the symmetry and balance of the isosceles trapezoid but also play a significant role in various geometric calculations and constructions related to this shape.

Practical Examples and Problem Solving
Applying the concept of the perimeter of an isosceles trapezoid to practical examples enhances understanding and problem-solving skills. Here are some illustrative examples:
- Example 1: Find the perimeter of an isosceles trapezoid with bases of 20 inches and 25 inches, and non-parallel sides of 30 inches each. Using the formula ( P = a + b + 2c ), we calculate: ( P = 20 + 25 + 2 imes 30 = 105 ) inches.
- Example 2: If an isosceles trapezoid has a perimeter of 67.3 cm with one base of 30 cm, the other base of 18.3 cm, and leg length of 9.5 cm, verify this using the formula. Calculation: ( P = 30 + 18.3 + 2 imes 9.5 = 67.3 ) cm.
- Problem Solving Strategy: To solve problems related to the perimeter of an isosceles trapezoid, identify the lengths of the bases and the legs first. Then apply the formula ( P = a + b + 2c ) where ( a ) and ( b ) are the bases, and ( c ) is the length of the legs.
These examples show how understanding the properties and formulas of isosceles trapezoids can be applied to solve real-world problems effectively.

Role of Base Angles in Isosceles Trapezoids
The base angles in isosceles trapezoids are a fundamental aspect of their geometry, offering insight into their properties and applications.
- Equal Base Angles: In isosceles trapezoids, the base angles are congruent. This means that each pair of angles sharing the same base (e.g., angles adjacent to the top base and angles adjacent to the bottom base) are equal in measure.
- Supplementary Angles: The angles adjacent to opposite bases are supplementary, meaning the sum of these angles is 180 degrees. This is due to the parallel nature of the bases in isosceles trapezoids.
- Proofs and Theorems: The property of equal base angles can be proven using various geometric theorems and is fundamental in understanding the structure of isosceles trapezoids.
- Impact on Diagonals: The equality of base angles in isosceles trapezoids also influences other properties, such as the congruence of diagonals.
- Applications in Problem Solving: Understanding the role of base angles is crucial in solving geometric problems involving isosceles trapezoids, particularly in calculating angles and sides.
This geometric characteristic of equal base angles not only defines the shape of isosceles trapezoids but also aids in various mathematical computations and proofs.

Understanding the Height of Isosceles Trapezoids
The height of an isosceles trapezoid is a key element in understanding its geometry and calculating its area. The height is defined as the perpendicular distance between the two parallel bases.
- Calculating Height: To find the height of an isosceles trapezoid, if the area and the lengths of the bases are known, the height can be calculated using the formula: ( h = frac{2A}{a + b} ), where ( A ) is the area, and ( a ) and ( b ) are the lengths of the bases.
- Height and Diagonals: When the diagonals and one of the base lengths are known, the height can be determined using trigonometric calculations or Pythagoras\" theorem. For example, if the diagonal lengths and one base length are known, the other base can be calculated, which can then help to determine the height.
- Height and Perimeter: If the perimeter and the lengths of the legs are known, the base lengths can be determined, which in turn helps to find the height.
- Geometric Significance: The height is crucial for determining the area of the trapezoid and is a fundamental aspect in various geometrical problems and proofs related to isosceles trapezoids.
Understanding how to calculate and apply the concept of height is essential for solving problems related to isosceles trapezoids, including area and volume calculations in practical applications.
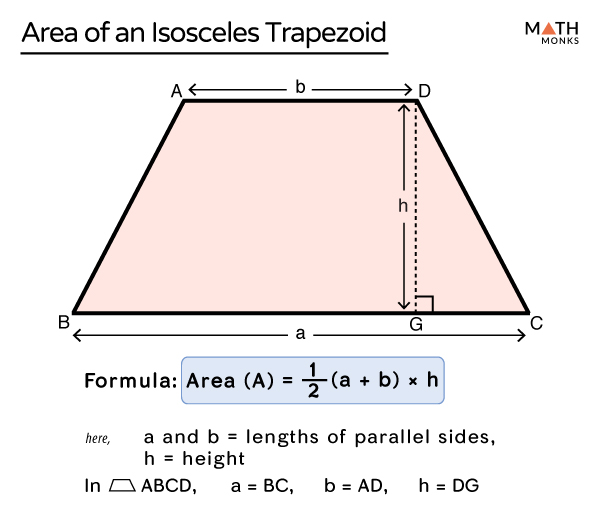
Advanced Calculations: Area, Diagonals, and More
Performing advanced calculations for isosceles trapezoids involves understanding their area, diagonal properties, and more intricate aspects of their geometry.
- Area Calculation: The area of an isosceles trapezoid can be calculated using the formula: ( Area = frac{(a+b)}{2} imes h ), where ( a ) and ( b ) are the lengths of the parallel bases, and ( h ) is the height.
- Diagonal Properties: The diagonals of an isosceles trapezoid are congruent and divide each other into segments of equal length. The length of each diagonal can be found using Ptolemy\"s theorem, involving the lengths of the parallel sides and the legs.
- Height Determination: The height can be found using the Pythagorean theorem, especially when the lengths of the diagonals and bases are known.
- Advanced Theorems: Utilizing advanced theorems such as the Pythagorean theorem or trigonometric functions helps in determining unknown dimensions of the trapezoid.
- Calculating Diagonals: The diagonals can be calculated using geometric formulas, which involve the sides of the trapezoid and its angles.
- Perimeter Calculation: The perimeter is calculated as the sum of all sides of the isosceles trapezoid. It can be represented as ( P = a + b + 2c ), where ( c ) is the length of the non-parallel sides (legs).
These advanced calculations are pivotal for comprehensive understanding and application in geometrical problems involving isosceles trapezoids.

_HOOK_
READ MORE:
Frequently Asked Questions About Isosceles Trapezoids
- What is an Isosceles Trapezoid?
- An isosceles trapezoid is a quadrilateral with one pair of parallel sides (bases) and non-parallel sides (legs) that are equal in length. It often has a line of symmetry and congruent base angles.
- How Do You Calculate the Area of an Isosceles Trapezoid?
- The area is calculated using the formula: ( Area = frac{(a + b)}{2} imes h ), where ( a ) and ( b ) are the lengths of the parallel bases, and ( h ) is the height.
- Are the Diagonals of an Isosceles Trapezoid Congruent?
- Yes, the diagonals of an isosceles trapezoid are congruent and divide each other into segments of equal length.
- How Do You Find the Height of an Isosceles Trapezoid?
- The height can be found using the Pythagorean theorem, especially if the lengths of the diagonals and one base are known, or by using the area formula rearranged to solve for the height.
- What Makes an Isosceles Trapezoid Different from a Regular Trapezoid?
- In an isosceles trapezoid, the non-parallel sides are equal in length and the base angles are congruent, which is not necessarily the case in a regular trapezoid.
- Can an Isosceles Trapezoid Be a Parallelogram?
- An isosceles trapezoid is not a parallelogram because it has only one pair of parallel sides, whereas a parallelogram has two pairs of parallel sides.
In conclusion, mastering the perimeter of an isosceles trapezoid unravels a world of geometric beauty and practical application, offering insights that blend mathematical theory with real-world problem-solving.