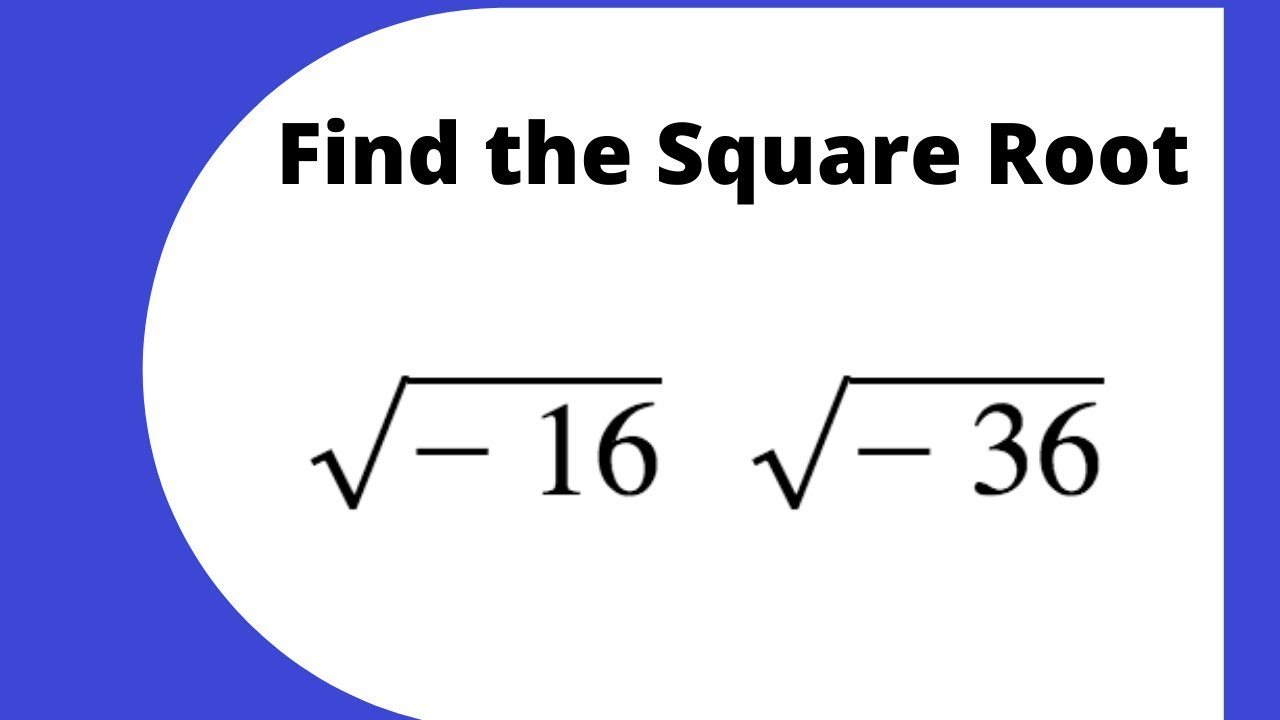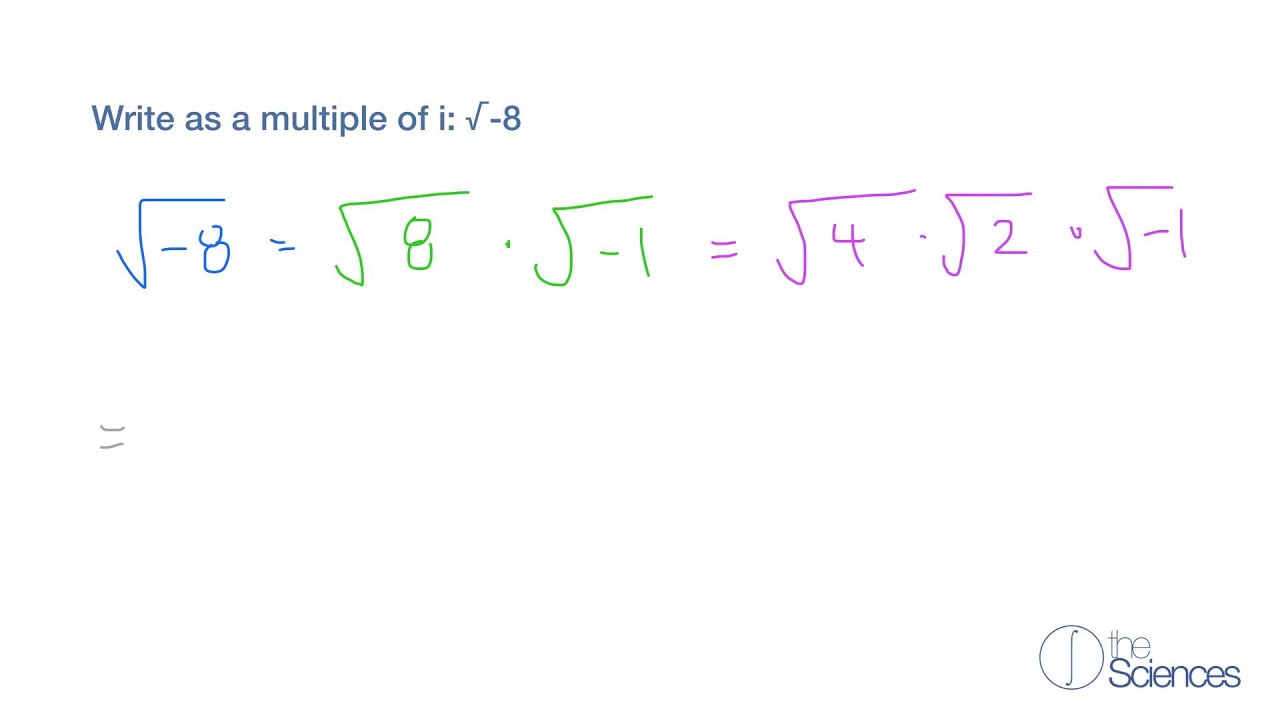Topic square root of 1 to 25: Unlock the fascinating world of square roots with our comprehensive guide on the square root of numbers from 1 to 25. Whether you're a student, educator, or math enthusiast, this article provides clear explanations, practical applications, and interesting trivia to enhance your understanding of these fundamental mathematical concepts.
Table of Content
- Square Root of Numbers from 1 to 25
- Introduction to Square Roots
- Understanding the Concept of Square Roots
- Methods to Calculate Square Roots
- Square Roots of Perfect Squares from 1 to 25
- Detailed Square Root Calculations
- 1. Square Root of 1
- 2. Square Root of 2
- 3. Square Root of 3
- 4. Square Root of 4
- 5. Square Root of 5
- 6. Square Root of 6
- 7. Square Root of 7
- 8. Square Root of 8
- 9. Square Root of 9
- 10. Square Root of 10
- 11. Square Root of 11
- 12. Square Root of 12
- 13. Square Root of 13
- YOUTUBE: Video hướng dẫn tính bình phương của các số từ 1 đến 25, phù hợp cho việc học toán và nâng cao kiến thức về số học.
Square Root of Numbers from 1 to 25
Understanding the square roots of numbers from 1 to 25 is fundamental in mathematics, especially in algebra and geometry. The square root of a number is a value that, when multiplied by itself, gives the original number. Below is a detailed table and explanations for the square roots of numbers from 1 to 25.
Table of Square Roots from 1 to 25
| Number | Square Root |
|---|---|
| 1 | \(\sqrt{1} = 1\) |
| 2 | \(\sqrt{2} \approx 1.414\) |
| 3 | \(\sqrt{3} \approx 1.732\) |
| 4 | \(\sqrt{4} = 2\) |
| 5 | \(\sqrt{5} \approx 2.236\) |
| 6 | \(\sqrt{6} \approx 2.449\) |
| 7 | \(\sqrt{7} \approx 2.646\) |
| 8 | \(\sqrt{8} \approx 2.828\) |
| 9 | \(\sqrt{9} = 3\) |
| 10 | \(\sqrt{10} \approx 3.162\) |
| 11 | \(\sqrt{11} \approx 3.317\) |
| 12 | \(\sqrt{12} \approx 3.464\) |
| 13 | \(\sqrt{13} \approx 3.606\) |
| 14 | \(\sqrt{14} \approx 3.742\) |
| 15 | \(\sqrt{15} \approx 3.873\) |
| 16 | \(\sqrt{16} = 4\) |
| 17 | \(\sqrt{17} \approx 4.123\) |
| 18 | \(\sqrt{18} \approx 4.243\) |
| 19 | \(\sqrt{19} \approx 4.359\) |
| 20 | \(\sqrt{20} \approx 4.472\) |
| 21 | \(\sqrt{21} \approx 4.583\) |
| 22 | \(\sqrt{22} \approx 4.690\) |
| 23 | \(\sqrt{23} \approx 4.796\) |
| 24 | \(\sqrt{24} \approx 4.899\) |
| 25 | \(\sqrt{25} = 5\) |
Examples and Applications
Square roots have numerous applications in mathematics and real-life situations. Here are a few examples:
- Geometry: The length of the diagonal of a square with side length \(a\) can be found using the square root: \(\sqrt{2a^2} = a\sqrt{2}\).
- Physics: Calculating the root mean square velocity of gas particles involves taking the square root of the average of the squares of velocities.
- Engineering: Determining the stress and strain in materials often requires the use of square roots.
Visual Representation
Square roots can also be represented visually, making it easier to understand their properties and relationships. For instance, the square root of 9 is the length of each side of a square with an area of 9 square units.
By mastering the square roots of numbers from 1 to 25, students can enhance their mathematical skills and apply this knowledge to more advanced topics.

READ MORE:
Introduction to Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. It is a fundamental concept in mathematics with applications in various fields such as algebra, geometry, and engineering. The square root of a number \( x \) is represented as \( \sqrt{x} \).
For example:
- \(\sqrt{1} = 1\) because \(1 \times 1 = 1\)
- \(\sqrt{4} = 2\) because \(2 \times 2 = 4\)
- \(\sqrt{9} = 3\) because \(3 \times 3 = 9\)
Square roots can be classified into two categories:
- Perfect Squares: Numbers whose square roots are whole numbers. For example, 1, 4, 9, 16, and 25 are perfect squares.
- Non-Perfect Squares: Numbers whose square roots are not whole numbers and are represented as decimals or fractions. For example, 2, 3, 5, and 7 are non-perfect squares.
The square root function is the inverse of the squaring function. If \( y = x^2 \), then \( x = \sqrt{y} \).
Here is a table showing the square roots of numbers from 1 to 25:
| Number | Square Root |
| 1 | \(\sqrt{1} = 1\) |
| 2 | \(\sqrt{2} \approx 1.414\) |
| 3 | \(\sqrt{3} \approx 1.732\) |
| 4 | \(\sqrt{4} = 2\) |
| 5 | \(\sqrt{5} \approx 2.236\) |
| 6 | \(\sqrt{6} \approx 2.449\) |
| 7 | \(\sqrt{7} \approx 2.646\) |
| 8 | \(\sqrt{8} \approx 2.828\) |
| 9 | \(\sqrt{9} = 3\) |
| 10 | \(\sqrt{10} \approx 3.162\) |
| 11 | \(\sqrt{11} \approx 3.317\) |
| 12 | \(\sqrt{12} \approx 3.464\) |
| 13 | \(\sqrt{13} \approx 3.606\) |
| 14 | \(\sqrt{14} \approx 3.742\) |
| 15 | \(\sqrt{15} \approx 3.873\) |
| 16 | \(\sqrt{16} = 4\) |
| 17 | \(\sqrt{17} \approx 4.123\) |
| 18 | \(\sqrt{18} \approx 4.243\) |
| 19 | \(\sqrt{19} \approx 4.359\) |
| 20 | \(\sqrt{20} \approx 4.472\) |
| 21 | \(\sqrt{21} \approx 4.583\) |
| 22 | \(\sqrt{22} \approx 4.690\) |
| 23 | \(\sqrt{23} \approx 4.796\) |
| 24 | \(\sqrt{24} \approx 4.899\) |
| 25 | \(\sqrt{25} = 5\) |
Understanding square roots is essential for solving various mathematical problems and real-world applications. By mastering this concept, you can enhance your problem-solving skills and mathematical reasoning.
Understanding the Concept of Square Roots
Square roots are fundamental mathematical operations that reverse the process of squaring a number. To find the square root of a number means determining a value that, when multiplied by itself, equals the original number. The square root of a number \( x \) is denoted as \( \sqrt{x} \) and is defined as follows:
If \( y^2 = x \), then \( y = \sqrt{x} \).
For example:
- \(\sqrt{4} = 2\) because \(2 \times 2 = 4\).
- \(\sqrt{9} = 3\) because \(3 \times 3 = 9\).
- \(\sqrt{16} = 4\) because \(4 \times 4 = 16\).
Square roots can be visualized geometrically. Consider a square with an area of \( A \) square units. The length of each side of the square is the square root of \( A \). For instance, a square with an area of 25 square units has sides of length 5 units, since \( \sqrt{25} = 5 \).
Here are some key points to understand about square roots:
- Positive and Negative Roots: Every positive number has two square roots: one positive and one negative. For example, \( \sqrt{25} = 5 \) and \( \sqrt{25} = -5 \).
- Zero: The square root of zero is zero, \( \sqrt{0} = 0 \).
- Non-Negative Numbers: The principal square root of a number is always non-negative. When we refer to \( \sqrt{x} \), we usually mean the principal (positive) square root.
- Irrational Numbers: The square roots of most non-perfect squares are irrational numbers. For example, \( \sqrt{2} \approx 1.414 \), and it cannot be expressed as an exact fraction.
To better understand square roots, consider this table showing the square roots of numbers from 1 to 25:
| Number | Square Root |
| 1 | \(\sqrt{1} = 1\) |
| 2 | \(\sqrt{2} \approx 1.414\) |
| 3 | \(\sqrt{3} \approx 1.732\) |
| 4 | \(\sqrt{4} = 2\) |
| 5 | \(\sqrt{5} \approx 2.236\) |
| 6 | \(\sqrt{6} \approx 2.449\) |
| 7 | \(\sqrt{7} \approx 2.646\) |
| 8 | \(\sqrt{8} \approx 2.828\) |
| 9 | \(\sqrt{9} = 3\) |
| 10 | \(\sqrt{10} \approx 3.162\) |
| 11 | \(\sqrt{11} \approx 3.317\) |
| 12 | \(\sqrt{12} \approx 3.464\) |
| 13 | \(\sqrt{13} \approx 3.606\) |
| 14 | \(\sqrt{14} \approx 3.742\) |
| 15 | \(\sqrt{15} \approx 3.873\) |
| 16 | \(\sqrt{16} = 4\) |
| 17 | \(\sqrt{17} \approx 4.123\) |
| 18 | \(\sqrt{18} \approx 4.243\) |
| 19 | \(\sqrt{19} \approx 4.359\) |
| 20 | \(\sqrt{20} \approx 4.472\) |
| 21 | \(\sqrt{21} \approx 4.583\) |
| 22 | \(\sqrt{22} \approx 4.690\) |
| 23 | \(\sqrt{23} \approx 4.796\) |
| 24 | \(\sqrt{24} \approx 4.899\) |
| 25 | \(\sqrt{25} = 5\) |
Understanding square roots helps in solving equations, simplifying expressions, and analyzing geometric properties. It is a vital tool in various branches of mathematics and science, fostering a deeper comprehension of numerical relationships.
Methods to Calculate Square Roots
Calculating square roots can be approached using several methods, each suitable for different types of numbers and precision requirements. Here are some commonly used methods:
1. Prime Factorization Method
This method is most effective for perfect squares. It involves breaking down the number into its prime factors and pairing them to find the square root.
- Example: To find the square root of 81:
- Prime factorization of 81 is \(3 \times 3 \times 3 \times 3\).
- Pair the prime factors: \(81 = (3 \times 3) \times (3 \times 3) = 9 \times 9\).
- The square root of 81 is 9.
2. Long Division Method
This method is useful for both perfect and imperfect squares, providing a systematic way to find square roots with high precision.
- Example: To find the square root of 2:
- Write the number as 2.00000000.
- Group the digits in pairs from the decimal point: 2.00 | 00 | 00 | 00.
- Find the largest number whose square is less than or equal to the first group: 1 (since \(1^2 = 1\)).
- Subtract and bring down the next pair of zeros: \(2 - 1 = 1\); new number is 100.
- Double the divisor (1 becomes 2) and find the largest digit \(x\) such that \(2x \times x \leq 100\). The digit is 4, and \(24 \times 4 = 96\).
- Repeat the process to obtain more decimal places.
- The approximate square root of 2 is 1.4142.
3. Repeated Subtraction Method
This method is simple but limited to finding square roots of perfect squares by repeatedly subtracting consecutive odd numbers until reaching zero.
- Example: To find the square root of 25:
- 25 - 1 = 24
- 24 - 3 = 21
- 21 - 5 = 16
- 16 - 7 = 9
- 9 - 9 = 0
- Since we reached zero in the 5th step, the square root of 25 is 5.
4. Using a Calculator
The easiest and most accurate method for finding square roots of any number is to use a calculator. Most calculators have a square root function (√) that quickly provides the result.
- Example: To find the square root of 10 using a calculator, simply press the √ button followed by 10, and the calculator will display approximately 3.1623.
5. Estimation and Refinement
This method involves estimating the square root and then refining the estimate using arithmetic mean.
- Example: To find the square root of 10:
- Estimate: Since \(3^2 = 9\) and \(4^2 = 16\), √10 is between 3 and 4.
- Refinement: Try 3.5: \(3.5 \times 3.5 = 12.25\) (too high). Try 3.2: \(3.2 \times 3.2 = 10.24\) (still high).
- Continue refining until the desired precision is reached, e.g., \(3.162\).
Square Roots of Perfect Squares from 1 to 25
Understanding the square roots of perfect squares between 1 and 25 helps in various mathematical calculations and problem-solving scenarios. Here, we list the square roots of the perfect squares in this range.
| Number | Square Root |
|---|---|
| 1 | \(\sqrt{1} = 1\) |
| 4 | \(\sqrt{4} = 2\) |
| 9 | \(\sqrt{9} = 3\) |
| 16 | \(\sqrt{16} = 4\) |
| 25 | \(\sqrt{25} = 5\) |
The table above shows that the perfect squares between 1 and 25 have integer square roots. These values are fundamental in mathematics, making computations involving areas and roots straightforward. Let's briefly discuss the concept of perfect squares and their properties:
- Definition: A perfect square is an integer that is the square of another integer. For instance, 16 is a perfect square because it equals \(4^2\).
- Properties: Perfect squares always have an odd number of total factors. They can be visually represented as a square area with sides of integer lengths.
- Examples in Real Life: Perfect squares appear in various real-world scenarios, such as determining the side length of a square given its area.
Understanding these square roots helps in simplifying radical expressions and solving quadratic equations. In real-life applications, knowing the square roots of these numbers can assist in geometry, physics, engineering, and various fields that require mathematical calculations.

Detailed Square Root Calculations
Calculating the square root of a number involves finding a value that, when multiplied by itself, gives the original number. Here, we will provide detailed calculations for the square roots of numbers from 1 to 25.
- Square Root of 1:
\(\sqrt{1} = 1\)
- Square Root of 2:
Approximate value: \(\sqrt{2} \approx 1.414\)
- Square Root of 3:
Approximate value: \(\sqrt{3} \approx 1.732\)
- Square Root of 4:
\(\sqrt{4} = 2\)
- Square Root of 5:
Approximate value: \(\sqrt{5} \approx 2.236\)
- Square Root of 6:
Approximate value: \(\sqrt{6} \approx 2.449\)
- Square Root of 7:
Approximate value: \(\sqrt{7} \approx 2.646\)
- Square Root of 8:
Approximate value: \(\sqrt{8} \approx 2.828\)
- Square Root of 9:
\(\sqrt{9} = 3\)
- Square Root of 10:
Approximate value: \(\sqrt{10} \approx 3.162\)
- Square Root of 11:
Approximate value: \(\sqrt{11} \approx 3.317\)
- Square Root of 12:
Approximate value: \(\sqrt{12} \approx 3.464\)
- Square Root of 13:
Approximate value: \(\sqrt{13} \approx 3.606\)
- Square Root of 14:
Approximate value: \(\sqrt{14} \approx 3.742\)
- Square Root of 15:
Approximate value: \(\sqrt{15} \approx 3.873\)
- Square Root of 16:
\(\sqrt{16} = 4\)
- Square Root of 17:
Approximate value: \(\sqrt{17} \approx 4.123\)
- Square Root of 18:
Approximate value: \(\sqrt{18} \approx 4.243\)
- Square Root of 19:
Approximate value: \(\sqrt{19} \approx 4.359\)
- Square Root of 20:
Approximate value: \(\sqrt{20} \approx 4.472\)
- Square Root of 21:
Approximate value: \(\sqrt{21} \approx 4.583\)
- Square Root of 22:
Approximate value: \(\sqrt{22} \approx 4.690\)
- Square Root of 23:
Approximate value: \(\sqrt{23} \approx 4.796\)
- Square Root of 24:
Approximate value: \(\sqrt{24} \approx 4.899\)
- Square Root of 25:
\(\sqrt{25} = 5\)
These calculations can be verified using methods such as the long division method or prime factorization for more accurate results. For non-perfect squares, iterative methods like the Newton-Raphson method can be used to find more precise values.
1. Square Root of 1
The square root of a number is a value that, when multiplied by itself, gives the original number. The square root of 1 is particularly simple and important in mathematics. Below is a detailed explanation of how to determine and understand the square root of 1.
Definition:
The square root of 1, denoted as √1, is the number that, when multiplied by itself, equals 1.
Mathematically, this can be written as:
$$\sqrt{1} = 1$$
Let's verify this:
$$1 \times 1 = 1$$
Therefore, the square root of 1 is indeed 1.
Prime Factorization Method
For the number 1, the prime factorization method is straightforward:
- Express 1 as a product of its prime factors:
Since 1 is a unique number that is both its own prime factor and its own square, this step is trivial. - Pair the prime factors:
Again, since 1 is its own factor, it is already paired.
Thus, the square root of 1 remains 1.
Properties of the Square Root of 1
- Identity Element: 1 is the multiplicative identity, meaning any number multiplied by 1 remains unchanged.
- Non-negative: The square root of 1 is always non-negative. Although technically -1 squared also equals 1, by convention, the principal square root (√) is always the non-negative value.
The square root of 1 is a simple yet fundamental concept in mathematics, serving as a basis for understanding more complex square roots and other mathematical operations.
2. Square Root of 2
The square root of 2 is an important irrational number, often represented as \( \sqrt{2} \) or 2½. Its value is approximately 1.414213562373095, though it extends infinitely without repeating.
Properties of \( \sqrt{2} \)
- It is an irrational number, meaning it cannot be expressed as a simple fraction.
- The decimal representation of \( \sqrt{2} \) is non-terminating and non-repeating.
- \( \sqrt{2} \) is also known as Pythagoras' constant.
- It represents the length of the diagonal of a unit square.
Calculating \( \sqrt{2} \)
There are several methods to approximate the value of \( \sqrt{2} \). Two common methods are:
1. Long Division Method
This method involves iterative steps to find the square root. Here's a simplified process:
- Estimate a number close to \( \sqrt{2} \) (e.g., 1.4).
- Divide 2 by this estimate (2 / 1.4 ≈ 1.4286).
- Average the result with the original estimate ((1.4 + 1.4286) / 2 ≈ 1.4143).
- Repeat the process until the desired accuracy is achieved.
2. Estimation and Approximation Method
This method uses iterative formulas to improve the estimate. The basic formula is:
\[ y_{n+1} = \frac{(x/y_n) + y_n}{2} \]
For \( \sqrt{2} \), start with \( y_1 = 1 \):
- Iteration 1: \( y_2 = \frac{(2/1) + 1}{2} = 1.5 \)
- Iteration 2: \( y_3 = \frac{(2/1.5) + 1.5}{2} ≈ 1.4167 \)
- Iteration 3: \( y_4 = \frac{(2/1.4167) + 1.4167}{2} ≈ 1.4142 \)
Applications of \( \sqrt{2} \)
The square root of 2 is widely used in geometry, especially in calculations involving right-angled triangles and squares. For example, it is used to determine the diagonal length of a square with sides of length 1:
\[ \text{Diagonal} = \sqrt{2} \]
Examples
- To find the length of the diagonal of a square with side length 2 units:
- Diagonal = \( \sqrt{2} \times 2 ≈ 2.828 \) units
- In an equilateral triangle with an area of \( 2\sqrt{3} \) square units:
- The side length \( a \) can be found using the formula for the area of an equilateral triangle, yielding \( a = 2\sqrt{2} ≈ 2.828 \) units.
3. Square Root of 3
The square root of 3, denoted as \( \sqrt{3} \), is an important mathematical constant. The value of \( \sqrt{3} \) is approximately 1.732. This value is widely used in various fields such as geometry, trigonometry, and engineering.
Since \( \sqrt{3} \) is an irrational number, it cannot be expressed exactly as a fraction and its decimal representation is non-terminating and non-repeating.
Approximate Value
The approximate value of \( \sqrt{3} \) is:
\[
\sqrt{3} \approx 1.732050807568877293527446341505872366 \ldots
\]
Long Division Method
To find the square root of 3 using the long division method, follow these steps:
- Start by pairing the digits from the decimal point, considering 3 as 3.000000...
- Find the largest number whose square is less than or equal to 3. In this case, 1 (since \(1^2 = 1\)).
- Subtract 1 from 3, bringing down two zeros, making it 200.
- Double the quotient (1), getting 2. Use 20 as the new divisor and find the number x such that 20x * x ≤ 200. The suitable number is 7 (since 207 * 7 = 1449 ≤ 2000).
- Repeat the process, bringing down pairs of zeros and finding suitable digits for each step.
This iterative process gives a more accurate value of \( \sqrt{3} \).
Geometric and Trigonometric Applications
- The height of an equilateral triangle with a side length of 2 is \( \sqrt{3} \).
- The long leg of a 30-60-90 triangle with a hypotenuse of 2 is \( \sqrt{3} \).
- The space diagonal of a unit cube is \( \sqrt{3} \).
Continued Fraction Representation
The square root of 3 can also be expressed as a continued fraction:
\[
\sqrt{3} = 1 + \frac{1}{1 + \frac{1}{2 + \frac{1}{1 + \frac{1}{2 + \cdots}}}}
\]
This representation provides another way to approximate the value of \( \sqrt{3} \) through an infinite series.
Use in Power Engineering
In power engineering, the voltage between two phases in a three-phase system is \( \sqrt{3} \) times the line to neutral voltage. This is due to the 120-degree separation between any two phases in a three-phase system.
Conclusion
The square root of 3 is a fundamental mathematical constant with numerous applications in geometry, trigonometry, and engineering. Its value can be approximated through various methods, including the long division method and continued fractions.

4. Square Root of 4
The square root of a number is a value that, when multiplied by itself, gives the original number. In the case of 4, we are looking for a number that satisfies the equation:
\( \sqrt{4} = ? \)
To find the square root of 4, let's use the following steps:
- Identify the square number: \(4\).
- Determine the number which, when multiplied by itself, equals 4.
The equation we need to solve is:
\( x^2 = 4 \)
This means we need to find \( x \) such that \( x \cdot x = 4 \). We can try a few values:
- \( 1 \cdot 1 = 1 \)
- \( 2 \cdot 2 = 4 \)
So, we find that \( 2 \) is the number that works. Therefore, the square root of 4 is:
\( \sqrt{4} = 2 \)
This can be verified by reversing the process:
\( 2 \cdot 2 = 4 \)
Additionally, we know that both \( +2 \) and \( -2 \) squared give 4, but by convention, we take the principal (non-negative) square root. Thus:
\( \sqrt{4} = 2 \)
For further understanding, consider the geometric interpretation: if you have a square with an area of 4 square units, each side of the square will be:
\( \sqrt{4} = 2 \) units
So, the square root of 4 is \( 2 \), which is a fundamental concept in mathematics, often used as a building block for understanding more complex operations involving square roots and exponents.
5. Square Root of 5
The square root of 5 is an irrational number, which means it cannot be expressed as a simple fraction and its decimal form is non-repeating and non-terminating. The approximate value of the square root of 5 is:
\(\sqrt{5} \approx 2.23607\)
Step-by-Step Calculation Using Long Division Method
One way to find the square root of 5 is by using the long division method. Here is a detailed step-by-step explanation:
- Setup: Write the number 5 under the square root symbol. Start grouping the digits in pairs from the decimal point, both to the left and the right. Since 5 is a single digit, it forms one group.
- Find the largest number: Find the largest number whose square is less than or equal to 5. This number is 2, since \(2^2 = 4\).
- Divide and Subtract: Subtract the square of 2 (which is 4) from 5 to get the remainder of 1.
- Bring down pairs of zeros: Bring down the next pair of digits (which is 00 in this case), making the new number 100.
- Double the quotient: The quotient so far is 2. Double it (2 * 2 = 4) and place it next to a blank digit to get 40_.
- Find the suitable digit: Find a digit \(d\) such that 40_d multiplied by \(d\) is less than or equal to 100. The suitable digit here is 2, making it 402 * 2 = 804.
- Repeat: Repeat the process: subtract, bring down pairs of zeros, find the next digit. This gives a more accurate approximation of the square root each time.
The more steps you perform, the more accurate the value you get. For practical purposes, stopping after a few decimal places is often sufficient.
Examples of Applications
Square roots are used in various fields such as mathematics, physics, engineering, and finance. For instance, the square root of 5 may be used in calculations involving quadratic equations, geometry (such as finding the diagonal of a rectangle with sides 1 and 2), and in statistical formulas.
Using a Calculator
To quickly find the square root of 5, you can use a scientific calculator. Simply press the square root button (√) and enter 5, which will give you the value approximately equal to 2.23607.
6. Square Root of 6
The square root of 6 is an irrational number, meaning it cannot be expressed exactly as a simple fraction. However, it can be approximated and calculated to a high degree of accuracy. Let's explore the methods to calculate and understand the square root of 6.
Approximate Value
The square root of 6 is approximately 2.449489742783178. This approximation can be useful for practical purposes where an exact value is not required.
Methods to Calculate
There are several methods to calculate the square root of 6, including:
-
Prime Factorization:
This method is most effective for perfect squares, but for non-perfect squares like 6, we use other methods.
-
Long Division Method:
This method involves a step-by-step manual process similar to long division in arithmetic, providing a decimal approximation.
-
Newton's Method (Newton-Raphson Method):
This iterative method can be used to find increasingly accurate approximations of the square root. Here’s how it works:
- Start with an initial guess \( x_0 \). A good starting point is 2.
- Use the formula \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{6}{x_n} \right) \).
- Repeat the process until the difference between successive approximations is less than the desired accuracy.
For example, starting with \( x_0 = 2 \):
- \( x_1 = \frac{1}{2} \left( 2 + \frac{6}{2} \right) = 2.5 \)
- \( x_2 = \frac{1}{2} \left( 2.5 + \frac{6}{2.5} \right) \approx 2.45 \)
- \( x_3 = \frac{1}{2} \left( 2.45 + \frac{6}{2.45} \right) \approx 2.4495 \)
Using a Calculator
The easiest and most accurate way to find the square root of 6 is by using a scientific calculator. Simply enter 6 and press the square root button to get the result, which will be displayed as approximately 2.44948974278.
Mathematical Expression with MathJax
We can represent the square root of 6 using MathJax for clarity in mathematical documents:
\(\sqrt{6} \approx 2.449489742783178\)
Applications
The square root of 6 can be used in various fields, such as engineering, physics, and computer science, where precise measurements and calculations are required.
7. Square Root of 7
The square root of 7 is an irrational number, which means it cannot be expressed as a simple fraction and its decimal representation is non-repeating and non-terminating. The approximate value of the square root of 7 is:
\[\sqrt{7} \approx 2.6457513110645906\]
Methods to Calculate the Square Root of 7
There are several methods to calculate the square root of 7. Here, we will discuss two common methods: the long division method and the approximation method.
1. Long Division Method
The long division method involves a series of steps to get a precise value of the square root. Here's how you can do it:
- Start by grouping the digits of the number in pairs, starting from the decimal point. For 7, we write it as 7.000000...
- Find the largest number whose square is less than or equal to 7. This number is 2 because \(2^2 = 4\).
- Subtract \(4\) from 7 to get the remainder 3, and bring down a pair of zeros to make it 300.
- Double the quotient (which is 2) and write it as 4, and think of a number (x) that, when placed next to 4, forms a number 4x such that 4x * x is less than or equal to 300. The number is 6 because 46 * 6 = 276.
- Subtract 276 from 300 to get 24, bring down another pair of zeros to make it 2400.
- Repeat the process to get more decimal places.
2. Approximation Method
An easier method for a quick approximation is to use the values of square roots of nearby perfect squares:
- \(\sqrt{4} = 2\)
- \(\sqrt{9} = 3\)
Since 7 lies between 4 and 9, \(\sqrt{7}\) will lie between 2 and 3. By averaging and iterating, we refine the value to approximately 2.646.
Properties of the Square Root of 7
- The square root of 7 is an irrational number.
- Its decimal expansion is non-terminating and non-repeating.
- When squared, it gives the original number: \((\sqrt{7})^2 = 7\).
Applications of the Square Root of 7
Understanding the square root of 7 is useful in various fields such as mathematics, physics, and engineering. It helps in solving equations, analyzing wave functions, and in geometric calculations.
Examples
Let's consider a few examples to illustrate the use of \(\sqrt{7}\):
- Geometry: Finding the length of the diagonal of a square with side length 7 units. The diagonal \(d\) is given by: \[ d = \sqrt{2} \times \text{side} = \sqrt{2} \times 7 = 7\sqrt{2} \approx 9.899 \text{ units}\]
- Algebra: Solving for \(x\) in the equation \(x^2 = 7\): \[ x = \sqrt{7} \approx 2.646 \]

8. Square Root of 8
The square root of 8 is an irrational number that can be approximated using various methods. Here, we will explore the value, calculation methods, and some interesting properties related to the square root of 8.
Value of Square Root of 8:
\(\sqrt{8} \approx 2.828\)
Methods to Calculate the Square Root of 8:
- Prime Factorization Method:
- Express 8 as a product of its prime factors: \(8 = 2 \times 2 \times 2 = 2^3\)
- Pair the prime factors to simplify: \( \sqrt{8} = \sqrt{2^3} = \sqrt{4 \times 2} = \sqrt{4} \times \sqrt{2} = 2 \sqrt{2} \)
- Since \( \sqrt{2} \approx 1.414\), we get \(2 \times 1.414 = 2.828\)
- Long Division Method:
The long division method involves a step-by-step process to find the decimal value of the square root:
- Set up the number 8 under the long division symbol.
- Find the largest number whose square is less than or equal to 8 (which is 2, since \(2^2 = 4\)).
- Subtract 4 from 8 to get the remainder 4. Bring down two zeros to make it 400.
- Double the quotient (which is 2) to get 4, and find the next digit such that when it's added to 40 (forming 40X) and multiplied by X, it gives a product less than or equal to 400.
- Repeat the steps to get more decimal places (2.828...).
Properties of the Square Root of 8:
- Irrational Number: The square root of 8 cannot be expressed as a fraction of two integers. It is a non-terminating, non-repeating decimal.
- Approximation: For practical purposes, \(\sqrt{8}\) is approximated as 2.828. This approximation is often sufficient for most calculations.
Applications:
- Geometry: The square root of 8 can be useful in geometric calculations, such as finding the diagonal of a square with sides of length 2 (since the diagonal is \(2 \sqrt{2}\)).
- Algebra: It appears in algebraic equations and can be used to simplify radical expressions.
Understanding and calculating the square root of 8 involves a combination of prime factorization, long division method, and recognizing its properties as an irrational number.
9. Square Root of 9
The square root of 9 is a fundamental concept in mathematics. The value is straightforward because 9 is a perfect square. Let's explore this in more detail:
When we talk about the square root of a number, we refer to a value that, when multiplied by itself, gives the original number. For 9, the square root is 3, since:
\[
3 \times 3 = 9
\]
To illustrate this further, let's break it down step by step:
-
Identify the number for which we need to find the square root, which is 9 in this case.
-
Find a number that, when multiplied by itself, equals 9. Here, it is 3 because:
\[
3^2 = 9
\] -
Therefore, the square root of 9 is:
\[
\sqrt{9} = 3
\]
It's important to note that the square root of a number can also be negative, as:
\[
(-3) \times (-3) = 9
\]
Thus,
\[
\sqrt{9} = \pm3
\]
However, in most cases, we consider the principal (positive) square root when we mention the square root of a number.
Understanding square roots is essential as it plays a crucial role in various mathematical applications, including algebra, geometry, and solving quadratic equations.
10. Square Root of 10
The square root of 10 is an important value in mathematics and has many practical applications. The square root of 10 is an irrational number, meaning it cannot be expressed as a simple fraction and its decimal representation is non-terminating and non-repeating. The approximate value of the square root of 10 is:
\[ \sqrt{10} \approx 3.162 \]
Understanding the Square Root of 10
The square root of 10 can be understood as the number that, when multiplied by itself, gives the product 10. This is mathematically represented as:
\[ \sqrt{10} \times \sqrt{10} = 10 \]
Methods to Calculate the Square Root of 10
There are several methods to calculate the square root of a number. For the square root of 10, the most common methods are:
- Prime Factorization: Since 10 is not a perfect square, prime factorization is not the most straightforward method here.
- Long Division Method: This is a more suitable method for finding the square root of non-perfect squares like 10.
Step-by-Step Calculation Using Long Division Method:
- Pair the digits of 10 from right to left: 10.00 (adding pairs of zeros for decimal places).
- Find the largest number whose square is less than or equal to 10. This number is 3 (since \(3^2 = 9\)).
- Subtract 9 from 10 to get 1 and bring down the next pair of zeros to get 100.
- Double the divisor (which is 3), getting 6. Place it next to the 3, making it 60.
- Find a digit (x) such that 60x multiplied by x is less than or equal to 100. The digit is 1, so the new divisor is 61, and 61*1=61.
- Subtract 61 from 100 to get 39, and bring down the next pair of zeros to get 3900.
- Repeat the process to get more decimal places.
Following this method, the value converges towards the approximate square root of 10:
\[ \sqrt{10} \approx 3.162 \]
Applications of the Square Root of 10
The square root of 10 appears in various mathematical contexts and real-world applications, such as:
- Engineering: In calculations involving waveforms and other periodic functions.
- Physics: When dealing with certain constants and in dimensional analysis.
- Statistics: In formulas related to standard deviation and variance.
Fun Fact
The number 10 is an important base in our number system, and its square root, while not a simple fraction, is crucial for understanding the properties of numbers around it.
11. Square Root of 11
The square root of 11 is an irrational number, meaning it cannot be expressed as a simple fraction and its decimal form is non-repeating and non-terminating. The approximate value of the square root of 11 is:
\[
\sqrt{11} \approx 3.317
\]
Methods to Calculate the Square Root of 11
There are various methods to calculate or approximate the square root of 11:
- Prime Factorization Method:
This method is not suitable for 11 because 11 is a prime number and cannot be broken down into smaller prime factors that pair up. Hence, we use other methods.
- Long Division Method:
The long division method is an effective way to find the square root of non-perfect squares. Here’s a step-by-step outline:
- Write 11 as 11.000000 to facilitate the calculation of decimal places.
- Start pairing the digits from the decimal point, moving to the left and to the right.
- Find a number (N) such that \( N \times N \leq 11 \). In this case, \( N \) is 3, because \( 3 \times 3 = 9 \) and \( 4 \times 4 = 16 \) which is greater than 11.
- Subtract \( 9 \) (which is \( 3 \times 3 \)) from 11 to get 2. Bring down the next pair of zeros to make it 200.
- Double the quotient (which is 3), and write it as 6 on the left side. Find a digit (D) such that \( 60D \times D \leq 200 \). The digit D is 3 because \( 603 \times 3 = 1809 \).
- Repeat the process to get more decimal places.
Representation of \(\sqrt{11}\) on a Number Line
To represent \(\sqrt{11}\) on a number line:
- Identify the integers between which \(\sqrt{11}\) lies. It is between 3 and 4 because \(3^2 = 9\) and \(4^2 = 16\).
- Divide the segment between 3 and 4 into ten equal parts to get decimal places.
- Identify the approximate position at 3.3 to represent \(\sqrt{11}\).
Applications of \(\sqrt{11}\)
The square root of 11 can be found in various real-world contexts, such as in geometry when calculating the diagonal of a rectangle or in physics problems involving distances and forces.
| Square Root | Value |
|---|---|
| \(\sqrt{11}\) | 3.317 |
In conclusion, understanding and calculating the square root of 11 is useful in many mathematical and practical applications.

12. Square Root of 12
The square root of 12 is an important mathematical value often encountered in various calculations. It is not a perfect square, which means its square root is an irrational number and cannot be expressed as a simple fraction.
To find the square root of 12, we can use the long division method or estimate its value using prime factorization. Here’s a detailed step-by-step method:
Prime Factorization Method
- Express 12 as a product of its prime factors:
- 12 = 2 × 2 × 3
- Pair the prime factors:
- 12 = (2 × 2) × 3 = 4 × 3
- Take the square root of each pair and multiply:
- \(\sqrt{12} = \sqrt{4 \times 3} = \sqrt{4} \times \sqrt{3} = 2 \times \sqrt{3}\)
Since \(\sqrt{3}\) is approximately 1.732, the square root of 12 is:
\(\sqrt{12} \approx 2 \times 1.732 = 3.464\)
Decimal Approximation
Using a calculator or numerical methods, we find that:
\(\sqrt{12} \approx 3.464\)
Properties and Applications
- The square root of 12 is used in various geometric calculations, such as finding the diagonal of a square with a side length of 6, since \(\sqrt{36} = 6\sqrt{2}\), and we know that \(\sqrt{12} = 6 / \sqrt{2}\).
- It appears in algebraic equations and functions involving roots and powers.
Understanding the square root of 12 and how to calculate it can be beneficial for solving complex mathematical problems and performing accurate measurements in both academic and practical fields.
13. Square Root of 13
The square root of 13 is an irrational number, meaning it cannot be expressed as a simple fraction and its decimal representation is non-repeating and non-terminating. The approximate value of the square root of 13 is:
\[
\sqrt{13} \approx 3.605551275
\]
To find the square root of 13 step-by-step, we can use the long division method. Here's how you can do it:
- Set up the long division: Start by pairing the digits from right to left. For 13, we pair it as (13).
- Find the largest number: Determine the largest number whose square is less than or equal to 13. In this case, 3 is the largest number because \(3^2 = 9\) which is less than 13.
- Divide: Subtract \(9\) from \(13\), which gives \(4\). Bring down a pair of zeros, making it \(400\).
- Double the divisor: Double the number found in step 2 (3) to get 6. Use 60 as a new divisor. Find the largest number \(x\) such that \(60x \times x \leq 400\). Here, \(60 \times 6 \leq 400\), so the next digit is 6.
- Repeat the process: Continue this process to get more decimal places as needed. This process will provide the approximate value of \(\sqrt{13}\).
Below is a table showing the values of the square roots of numbers around 13 for comparison:
| Number | Square Root |
|---|---|
| 12 | \(\sqrt{12} \approx 3.464\) |
| 13 | \(\sqrt{13} \approx 3.606\) |
| 14 | \(\sqrt{14} \approx 3.742\) |
Understanding the square root of 13 is helpful in various mathematical calculations and real-world applications. With practice, you can become proficient at estimating and calculating square roots of other non-perfect squares.
Video hướng dẫn tính bình phương của các số từ 1 đến 25, phù hợp cho việc học toán và nâng cao kiến thức về số học.
Hướng dẫn Tính Bình Phương từ 1 đến 25/1² đến 25²/Bình Phương của 1 đến 25
READ MORE:
Video hướng dẫn tính căn bậc hai của các số từ 1 đến 25, giúp người xem hiểu rõ và ứng dụng vào việc học toán.
Căn Bậc Hai của 1 đến 25