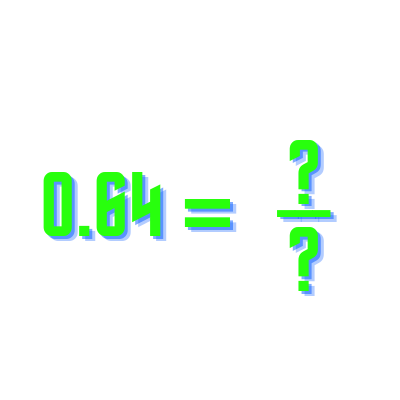How to Simplify Square Root 90: Easy Step-by-Step Guide

The square root of 90 can be simplified as follows:

\[ \sqrt{90} = \sqrt{9 \times 10} = \sqrt{9} \times \sqrt{10} = 3\sqrt{10} \]

Therefore, the simplified form of \( \sqrt{90} \) is \( 3\sqrt{10} \).

Simplifying square roots is a fundamental skill in mathematics that involves reducing a square root to its simplest form. This process helps in solving equations more easily and understanding the properties of numbers better. Here, we'll explore the steps to simplify the square root of 90, a common example used in various math problems.

To simplify a square root, follow these general steps:

1. Identify the factors of the number under the square root.
2. Look for perfect square factors.
3. Rewrite the square root as a product of the square root of these factors.
4. Simplify the expression by taking the square root of the perfect square factors.

Let's apply these steps to simplify the square root of 90:

• Step 1: Identify the factors of 90.
• Step 2: The factors of 90 are 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, and 90.
• Step 3: Identify the largest perfect square factor. Here, it is 9, since \(9 = 3^2\).
• Step 4: Rewrite \( \sqrt{90} \) as \( \sqrt{9 \times 10} \).
• Step 5: Separate the square root into \( \sqrt{9} \) and \( \sqrt{10} \).
• Step 6: Simplify \( \sqrt{9} \) to 3, so \( \sqrt{90} = 3\sqrt{10} \).

Therefore, the simplified form of \( \sqrt{90} \) is \( 3\sqrt{10} \). This process helps in breaking down complex square roots into simpler, more manageable parts, making calculations easier and more intuitive.

Square roots are mathematical expressions that represent a value which, when multiplied by itself, gives the original number. The square root of a number \(x\) is denoted as \( \sqrt{x} \). For example, \( \sqrt{25} = 5 \) because \( 5 \times 5 = 25 \).

Here are key concepts to understand square roots better:

• Perfect Squares: Numbers like 1, 4, 9, 16, and 25 are perfect squares because they can be expressed as the product of an integer with itself (e.g., \( 4 = 2 \times 2 \), \( 16 = 4 \times 4 \)).
• Non-Perfect Squares: Numbers that are not perfect squares, such as 2, 3, 5, and 10, have square roots that are irrational numbers (e.g., \( \sqrt{2} \approx 1.414 \)).
• Principal Square Root: The non-negative square root of a number is called the principal square root. For example, the principal square root of 25 is 5, even though both \( 5 \) and \( -5 \) squared result in 25.

To further understand square roots, consider the following properties:

1. Product Property: The square root of a product is the product of the square roots. Mathematically, \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \).
2. Quotient Property: The square root of a quotient is the quotient of the square roots. Mathematically, \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \) for \( b \neq 0 \).
3. Simplifying Square Roots: Simplifying involves breaking down the number into its prime factors and pairing the prime factors into perfect squares.

For example, to understand the square root of 90:

• Prime factorize 90: \( 90 = 2 \times 3^2 \times 5 \).
• Apply the product property: \( \sqrt{90} = \sqrt{2 \times 3^2 \times 5} \).
• Separate the perfect square: \( \sqrt{90} = \sqrt{9 \times 10} = \sqrt{9} \times \sqrt{10} \).
• Simplify further: \( \sqrt{9} = 3 \), so \( \sqrt{90} = 3\sqrt{10} \).

By understanding these principles, you can simplify and work with square roots more effectively, enhancing your overall mathematical skills.

The square root of 90 is a value that, when multiplied by itself, gives the number 90. This can be represented mathematically as \( \sqrt{90} \). Since 90 is not a perfect square, its square root is an irrational number, meaning it cannot be expressed as a simple fraction and has a non-repeating, non-terminating decimal expansion.

To find the square root of 90, we can simplify it by using prime factorization:

1. Step 1: Prime factorize 90.

We find that 90 can be broken down into prime factors:

• 90 = 2 × 45
• 45 = 3 × 15
• 15 = 3 × 5

So, the prime factorization of 90 is \( 2 \times 3^2 \times 5 \).

2. Step 2: Identify perfect squares within the factors.

From the factorization, we see that \( 3^2 \) is a perfect square.

3. Step 3: Rewrite the square root of 90 using these factors.

We can express \( \sqrt{90} \) as \( \sqrt{2 \times 3^2 \times 5} \).

4. Step 4: Simplify the square root.

Separate the perfect square factor:

\( \sqrt{90} = \sqrt{3^2 \times 2 \times 5} = \sqrt{3^2} \times \sqrt{2 \times 5} \).

Simplify further:

\( \sqrt{90} = 3 \times \sqrt{10} \).

Therefore, the simplified form of the square root of 90 is \( 3\sqrt{10} \).

This means that while \( \sqrt{90} \) is approximately equal to 9.4868, the simplified radical form is \( 3\sqrt{10} \), which is often more useful in mathematical expressions and equations.

The prime factorization method is a systematic way to simplify the square root of a number. Here, we will apply this method to simplify the square root of 90.

1. Find the prime factors of 90:

   First, we break down 90 into its prime factors:

   • 90 ÷ 2 = 45
   • 45 ÷ 3 = 15
   • 15 ÷ 3 = 5
   • 5 ÷ 5 = 1

   So, the prime factors of 90 are 2, 3, 3, and 5. This can be expressed as:

   \[90 = 2^1 \times 3^2 \times 5^1\]

2. Group the factors in pairs:

   We look for pairs of prime factors. In this case, we have a pair of 3s. The prime factorization in pairs looks like this:

   \[90 = (3 \times 3) \times (2 \times 5)\]

3. Take one factor from each pair:

   From the pair of 3s, we take a single 3 out of the square root. The other factors (2 and 5) remain under the square root:

   \[\sqrt{90} = 3 \sqrt{2 \times 5}\]

4. Multiply the factors:

   The remaining factors under the square root can be multiplied together:

   \[\sqrt{2 \times 5} = \sqrt{10}\]

   Thus, the simplified form of the square root of 90 is:

   \[\sqrt{90} = 3 \sqrt{10}\]

Therefore, the square root of 90 simplified using the prime factorization method is \(3 \sqrt{10}\).

To simplify the square root of 90, follow these steps:

1. Factor 90 into its prime factors:

90 = 2 × 3² × 5

2. Rewrite the square root of the product:

\(\sqrt{90} = \sqrt{2 \times 3^2 \times 5}\)

3. Separate the square root into the product of square roots:

\(\sqrt{2 \times 3^2 \times 5} = \sqrt{3^2} \times \sqrt{2 \times 5}\)

4. Simplify the square root of the perfect square:

\(\sqrt{3^2} = 3\)

5. Combine the simplified square root with the remaining factors:

\(3 \times \sqrt{10} = 3\sqrt{10}\)

Therefore, the simplified form of \(\sqrt{90}\) is \(3\sqrt{10}\).

To simplify the square root of 90, we need to break down the number into its prime factors. Here are the steps:

1. List all factors of 90:

   1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90

2. Identify the perfect squares:

   From the list of factors, the perfect squares are 1 and 9.

3. Find the largest perfect square:

   The largest perfect square factor of 90 is 9.

4. Divide 90 by the largest perfect square:

   \( \frac{90}{9} = 10 \)

5. Calculate the square root of the perfect square:

   \( \sqrt{9} = 3 \)

6. Combine the results:

   \( \sqrt{90} = \sqrt{9 \times 10} = \sqrt{9} \times \sqrt{10} = 3\sqrt{10} \)

Therefore, the simplified form of \( \sqrt{90} \) is \( 3\sqrt{10} \).

Simplifying the square root of 90 involves using perfect squares to make the simplification process easier. Here is a step-by-step guide:

1. Identify the factors of 90: The first step is to find the factors of 90 that include a perfect square. We know that 90 can be factored into 9 and 10, where 9 is a perfect square.

2. Write 90 as a product of its factors: Express 90 as the product of 9 and 10:

   \[ \sqrt{90} = \sqrt{9 \times 10} \]

3. Use the property of square roots: The square root of a product is equal to the product of the square roots of the factors:

   \[ \sqrt{9 \times 10} = \sqrt{9} \times \sqrt{10} \]

4. Simplify the perfect square: Since 9 is a perfect square, we know its square root:

   \[ \sqrt{9} = 3 \]

   So, we can simplify the expression further:

   \[ \sqrt{9} \times \sqrt{10} = 3 \sqrt{10} \]

Therefore, the simplified form of \(\sqrt{90}\) is \(3 \sqrt{10}\). By recognizing the perfect square factor within 90, we were able to simplify the square root to a more manageable expression.

Understanding the properties and rules of square roots is essential for simplifying and working with radical expressions. Here are some fundamental properties and rules:

1. Definition of a Square Root

The square root of a number \( n \), written as \( \sqrt{n} \), is the positive number that, when multiplied by itself, gives \( n \). For example:

\(\sqrt{25} = 5\) because \( 5 \times 5 = 25 \).

2. Product Rule for Radicals

The square root of a product is equal to the product of the square roots of each factor:

\[
\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}
\]

For example:

\[
\sqrt{50} = \sqrt{25 \cdot 2} = \sqrt{25} \cdot \sqrt{2} = 5 \cdot \sqrt{2}
\]

3. Quotient Rule for Radicals

The square root of a quotient is equal to the quotient of the square roots of the numerator and the denominator:

\[
\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}
\]

For example:

\[
\sqrt{\frac{49}{4}} = \frac{\sqrt{49}}{\sqrt{4}} = \frac{7}{2}
\]

4. Simplifying Square Roots

To simplify a square root, factor the number into its prime factors and look for pairs of prime factors:

1. Write the number under the square root in terms of its prime factors.
2. Pair the prime factors.
3. Move one factor from each pair outside the square root.

For example, to simplify \( \sqrt{72} \):

\[
\sqrt{72} = \sqrt{2^3 \cdot 3^2} = \sqrt{(2 \cdot 2) \cdot 2 \cdot (3 \cdot 3)} = 2 \cdot 3 \cdot \sqrt{2} = 6 \sqrt{2}
\]

5. Adding and Subtracting Like Square Roots

Like square roots have the same radicand (the number under the square root). To add or subtract like square roots, treat them as like terms:

\[
3 \sqrt{2} + 4 \sqrt{2} = 7 \sqrt{2}
\]

\[
5 \sqrt{3} - 2 \sqrt{3} = 3 \sqrt{3}
\]

6. Rationalizing the Denominator

When a square root appears in the denominator, multiply the numerator and the denominator by a value that will eliminate the square root from the denominator:

\[
\frac{1}{\sqrt{2}} = \frac{1}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}
\]

By mastering these properties and rules, you will be able to simplify and manipulate square roots with greater ease and confidence.

There are several methods to simplify the square root of 90. Each method offers a unique approach, allowing for flexibility depending on the context and the required precision.

1. Estimation Method

This method involves making an educated guess and refining it:

1. Recognize that \( \sqrt{81} = 9 \) and \( \sqrt{100} = 10 \), so \( \sqrt{90} \) is between 9 and 10.
2. Refine the estimate by testing values between 9 and 10. For example, 9.5 is too high as \( 9.5^2 = 90.25 \), but 9.4 is too low as \( 9.4^2 = 88.36 \). Adjust until a satisfactory precision is reached.

2. Long Division Method

This traditional method provides a manual way to calculate square roots:

1. Set up 90.000000 and pair the digits from the decimal point.
2. Find the largest number whose square is less than or equal to 90, which is 9. Subtract \( 9^2 = 81 \) from 90 to get a remainder of 9.
3. Bring down the next pair of zeros to get 900.
4. Double the initial quotient (9) to get 18, then find the digit to append to 18 to form a new divisor such that \( 184 \times 4 = 736 \), which is close to 900.
5. Repeat this process to refine the quotient and get more decimal places.

3. Prime Factorization Method

As explained earlier, this method simplifies the square root by breaking down the number into its prime factors:

1. Express 90 as the product of its prime factors: \( 90 = 2 \times 3^2 \times 5 \).
2. Apply the square root to each factor: \( \sqrt{90} = \sqrt{2 \times 3^2 \times 5} = \sqrt{2} \times \sqrt{3^2} \times \sqrt{5} \).
3. Simplify to \( 3\sqrt{10} \).

4. Using a Calculator

For a quick and precise result, using a calculator is often the best choice:

• Simply enter 90 and press the square root button to get \( \sqrt{90} \approx 9.4868 \).

5. Newton's Method

Newton's Method (or the Newton-Raphson method) is an iterative technique to find successively better approximations to the roots (or zeroes) of a real-valued function:

1. Choose an initial guess (x₀). For \( \sqrt{90} \), start with x₀ = 9.5.
2. Use the formula: \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{90}{x_n} \right) \).
3. Repeat the iteration until the desired level of accuracy is reached. After a few iterations, you will converge to \( \sqrt{90} \approx 9.4868 \).

Simplifying square roots can sometimes lead to errors. Here are common mistakes to avoid when simplifying √90:

• Incorrect Factorization:

  Ensure you factorize the number correctly. For example, 90 can be factored as 9 × 10. Incorrect factorization can lead to wrong results.

• Forgetting Perfect Squares:

  Always check for the largest perfect square factor. For 90, the largest perfect square factor is 9, as \( 9 = 3^2 \).

• Incorrect Application of Square Root Rules:

  Remember the property \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \). For 90, this translates to \( \sqrt{90} = \sqrt{9 \times 10} = \sqrt{9} \times \sqrt{10} = 3\sqrt{10} \).

• Overcomplicating Simplification:

  Do not overcomplicate the process. Simplify step-by-step and verify each step. For example, \( \sqrt{90} = 3\sqrt{10} \) is straightforward when you follow the correct steps.

• Incorrect Final Answer:

  Always simplify to the final answer correctly. The simplified form of √90 should be \( 3\sqrt{10} \), not just 3 or √10.

Test your understanding of simplifying square roots with the following practice problems. Each problem is followed by its detailed solution to help you learn the process step-by-step.

Practice Problems

1. Simplify the square root of 50.
2. Find the simplified form of √72.
3. Simplify √200.
4. Simplify the square root of 45.
5. Find the simplified form of √108.

Solutions

1. Problem: Simplify the square root of 50.

   Solution:

   • Identify perfect square factors: \(50 = 25 \times 2\).
   • Use the property: \( \sqrt{ab} = \sqrt{a} \times \sqrt{b} \).
   • Thus, \( \sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} = 5\sqrt{2} \).

2. Problem: Simplify the square root of 72.

   Solution:

   • Identify perfect square factors: \(72 = 36 \times 2\).
   • Thus, \( \sqrt{72} = \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} = 6\sqrt{2} \).

3. Problem: Simplify the square root of 200.

   Solution:

   • Identify perfect square factors: \(200 = 100 \times 2\).
   • Thus, \( \sqrt{200} = \sqrt{100 \times 2} = \sqrt{100} \times \sqrt{2} = 10\sqrt{2} \).

4. Problem: Simplify the square root of 45.

   Solution:

   • Identify perfect square factors: \(45 = 9 \times 5\).
   • Thus, \( \sqrt{45} = \sqrt{9 \times 5} = \sqrt{9} \times \sqrt{5} = 3\sqrt{5} \).

5. Problem: Simplify the square root of 108.

   Solution:

   • Identify perfect square factors: \(108 = 36 \times 3\).
   • Thus, \( \sqrt{108} = \sqrt{36 \times 3} = \sqrt{36} \times \sqrt{3} = 6\sqrt{3} \).

Simplified square roots are used in various real-life applications across multiple fields. Understanding these applications can help illustrate the importance and practicality of mathematical concepts. Here are some notable examples:

• Construction and Architecture:

  In construction, square roots are used to calculate the length of diagonal braces, ensuring structures are built with precise measurements. For example, if a builder needs to find the length of a diagonal brace for a wall with sides of 6 feet and 8 feet, they can use the Pythagorean theorem: \( \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10 \) feet. This calculation helps maintain structural integrity.

• Finance:

  In finance, square roots are used to calculate the volatility of stock prices. The standard deviation, which is the square root of the variance, helps investors understand the risk associated with a particular investment. For example, if the variance of a stock's returns is 16, the standard deviation would be \( \sqrt{16} = 4 \), indicating the average deviation from the mean return.

• Physics and Engineering:

  Square roots are essential in physics for calculating various properties, such as the period of a pendulum, which is proportional to the square root of its length. For instance, if the length of a pendulum is 4 meters, the period \( T \) is calculated using the formula \( T = 2\pi \sqrt{\frac{L}{g}} \), where \( L \) is the length and \( g \) is the acceleration due to gravity.

• Navigation:

  In navigation, square roots are used to compute distances between points on a map. For example, to find the distance between two points with coordinates (3, 4) and (6, 8), you can use the distance formula \( \sqrt{(6-3)^2 + (8-4)^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \) units.

• Statistics:

  In statistics, square roots are used to calculate the standard deviation, providing insights into data variability. For example, if the variance of a data set is 25, the standard deviation is \( \sqrt{25} = 5 \), indicating how much individual data points deviate from the mean.

• Science and Medicine:

  In scientific research, square roots are used to determine quantities such as radiation dosage or sound intensity. For instance, the intensity of sound waves decreases with the square of the distance from the source, a principle crucial in acoustics and audio engineering.

• Computer Science:

  Square roots are used in algorithms for graphics, encryption, and more. For example, calculating the distance between two points in a 2D space in computer graphics often involves using the Pythagorean theorem.

These applications highlight the importance of understanding and simplifying square roots, demonstrating their relevance and utility in everyday life and various professional fields.

Here are some commonly asked questions about simplifying the square root of 90, along with their answers to help you better understand the process:

• Q: Why do we simplify square roots?

  A: Simplifying square roots helps in making calculations easier and expressions more manageable. It allows us to work with smaller numbers and recognize common patterns.

• Q: How do we know which factors to use when simplifying √90?

  A: To simplify √90, we look for perfect square factors. In this case, 90 can be factored into 9 and 10, where 9 is a perfect square. So, √90 = √(9×10) = √9 × √10 = 3√10.

• Q: What is the simplest form of √90?

  A: The simplest form of √90 is 3√10. This is because 90 can be broken down into 9 and 10, with 9 being a perfect square.

• Q: Are there other methods to simplify square roots?

  A: Yes, aside from factoring into perfect squares, you can also use prime factorization or estimation methods to simplify square roots.

• Q: Can √90 be simplified further?

  A: No, 3√10 is already in its simplest form. We have extracted all possible perfect square factors.

• Q: What are some common mistakes to avoid when simplifying square roots?

  A: A common mistake is not fully factoring the number into its prime factors or missing a perfect square factor. Always double-check your factorization.

The process of simplifying the square root of 90 involves breaking it down into more manageable parts using mathematical properties and methods. This comprehensive guide has covered the necessary steps and strategies to simplify √90 effectively.

Here’s a summary of the key points:

• Understanding Square Roots: A square root is a value that, when multiplied by itself, gives the original number.
• Prime Factorization Method: By finding the prime factors of 90, we can simplify the square root. The prime factorization of 90 is \(2 \times 3^2 \times 5\).
• Simplification Process: The square root of 90 can be simplified by identifying and separating the perfect squares. This gives us: \[ \sqrt{90} = \sqrt{2 \times 3^2 \times 5} = 3\sqrt{10}. \]
• Properties and Rules: Utilizing properties of square roots, such as \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\), helps in the simplification process.
• Alternative Methods: Other techniques like estimation and approximation can also be used for practical purposes when exact simplification isn't necessary.
• Common Mistakes: Avoid common errors such as incorrectly identifying factors or forgetting to simplify fully.
• Real-Life Applications: Simplified square roots are useful in various real-world scenarios, including engineering, physics, and architecture, where precise calculations are essential.

In conclusion, simplifying the square root of 90 involves using prime factorization and applying square root properties to reduce it to its simplest form: \(3\sqrt{10}\). Mastering this skill enhances mathematical understanding and problem-solving abilities, proving valuable in both academic and practical contexts.