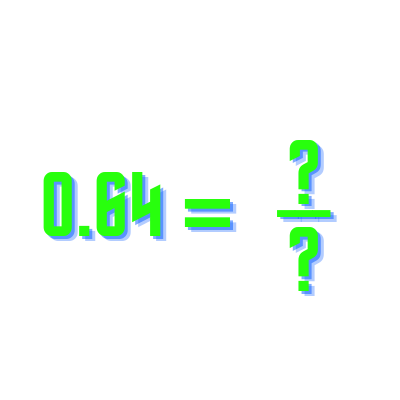Topic square root of 90 simplified radical form: The square root of 90 simplified into radical form reveals the essence of breaking down complex numbers into simpler, more manageable parts. This guide will walk you through understanding and simplifying √90 using various methods. Whether you are a student or a math enthusiast, mastering this skill will enhance your mathematical toolkit and boost your confidence.
Table of Content
- Square Root of 90 Simplified Radical Form
- Introduction to Square Roots and Radical Expressions
- Understanding the Concept of Simplifying Square Roots
- Step-by-Step Process to Simplify the Square Root of 90
- Prime Factorization Method to Simplify √90
- Using the Perfect Square Factors to Simplify √90
- Expressing √90 in Simplified Radical Form
- Comparison with Decimal Form: √90 ≈ 9.49
- Applications and Examples of Simplified Radicals
- Common Mistakes to Avoid When Simplifying Radicals
- Practice Problems for Simplifying Square Roots
- Further Resources and Reading on Radical Expressions
- Frequently Asked Questions about Simplifying Radicals
- Conclusion: Mastering the Simplification of √90
- YOUTUBE: Hướng dẫn cách đơn giản hóa căn bậc hai của 90 trong video này sẽ giúp bạn nắm vững các bước cơ bản và áp dụng dễ dàng vào bài toán.
Square Root of 90 Simplified Radical Form
The square root of 90 can be simplified to its simplest radical form. Here, we will demonstrate the steps involved in this simplification process and provide additional insights into the calculation.
Simplification Process
- Identify the factors of 90: 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90.
- Find the largest perfect square factor of 90, which is 9.
- Rewrite 90 as the product of 9 and 10: \( 90 = 9 \times 10 \).
- Take the square root of both factors: \( \sqrt{90} = \sqrt{9 \times 10} \).
- Simplify by taking the square root of 9: \( \sqrt{9} = 3 \).
- Express the simplified form: \( \sqrt{90} = 3\sqrt{10} \).
Mathematical Expressions
Using Mathjax, the simplified form of the square root of 90 is expressed as:
\[ \sqrt{90} = 3\sqrt{10} \]
Additional Information
- The square root of 90 in decimal form is approximately 9.486832980505138.
- It is an irrational number since it cannot be expressed as a simple fraction.
- In exponential form, the square root of 90 is written as \( 90^{1/2} \).
Example Problems
Here are a few examples that involve the square root of 90:
- Multiplication: \( \sqrt{90} \times \sqrt{75} = 3\sqrt{10} \times 5\sqrt{10} = 15 \times 10 = 150 \).
- Addition: \( \sqrt{90} + \sqrt{75} = 3\sqrt{10} + 5\sqrt{10} = 8\sqrt{10} \).
Interactive Question
Try simplifying the square root of other numbers. For example, simplify \( \sqrt{56} \).
- Simplified form: \( \sqrt{56} = 2\sqrt{14} \).
Conclusion
The square root of 90 simplifies to \( 3\sqrt{10} \). Understanding this process is crucial for solving various mathematical problems involving radicals.

READ MORE:
Introduction to Square Roots and Radical Expressions
Square roots and radical expressions are fundamental concepts in mathematics that involve finding a number which, when multiplied by itself, yields the original number. For instance, the square root of 9 is 3 because \( 3 \times 3 = 9 \). Radicals, symbolized by the square root sign \( \sqrt{} \), are used to represent these operations.
Understanding square roots is essential for simplifying expressions, solving equations, and handling various mathematical problems. Here, we will delve into the basics of square roots and explore how they are simplified into radical form.
- Square Root Notation: The square root of a number \( n \) is denoted as \( \sqrt{n} \). For example, \( \sqrt{16} = 4 \), since \( 4 \times 4 = 16 \).
- Perfect Squares: A perfect square is a number that has an integer as its square root. Examples include 1, 4, 9, 16, and 25. These numbers simplify neatly under the square root sign.
- Non-Perfect Squares: Numbers like 2, 3, and 90 are not perfect squares and do not simplify to whole numbers. These require us to find their simplified radical forms.
Radical expressions can sometimes be simplified to make them easier to work with. Simplifying involves finding factors of the number under the radical that are perfect squares.
| Example | Simplified Form |
| \( \sqrt{90} \) | \( \sqrt{9 \times 10} = 3\sqrt{10} \) |
| \( \sqrt{45} \) | \( \sqrt{9 \times 5} = 3\sqrt{5} \) |
| \( \sqrt{50} \) | \( \sqrt{25 \times 2} = 5\sqrt{2} \) |
To simplify a square root:
- Factor the number inside the radical into its prime factors.
- Pair the prime factors. Each pair of identical factors can be simplified outside the radical.
- Multiply the simplified factors outside the radical to obtain the final simplified form.
For instance, to simplify \( \sqrt{90} \), we find its prime factors: \( 90 = 2 \times 3^2 \times 5 \). We pair the \( 3 \)'s and take one outside the radical, resulting in \( 3\sqrt{10} \).
Understanding these fundamentals lays the groundwork for mastering more complex radical expressions and their simplifications.
Understanding the Concept of Simplifying Square Roots
Simplifying square roots involves rewriting a radical expression in its simplest form. This process helps to make complex numbers easier to work with, especially when they are not perfect squares. Let's explore the steps and methods used to simplify square roots.
When we talk about simplifying square roots, we essentially mean expressing them in the form \( a\sqrt{b} \), where \( a \) is an integer and \( b \) is a number that cannot be simplified further under the square root. Here's how to achieve this:
- Identify the Prime Factors: Start by finding the prime factors of the number under the square root. Prime factorization is the process of breaking down a number into its basic building blocks, which are prime numbers. For example, the prime factors of 90 are \( 2 \times 3^2 \times 5 \).
- Group the Factors: Once you have the prime factors, group them into pairs. Each pair of the same number under the radical can be simplified. For instance, in \( \sqrt{90} \), the prime factors \( 3 \times 3 \) can be paired.
- Simplify the Pairs: Each pair of factors comes out of the radical as a single number. So, \( \sqrt{3 \times 3} = 3 \). Using our example \( \sqrt{90} \), the pair of 3s simplifies to 3 outside the radical, leaving the 2 and 5 inside.
- Combine the Simplified Parts: Multiply the numbers outside the radical. If any factors are left inside the radical, multiply them as well. For \( \sqrt{90} \), after simplifying, we get \( 3\sqrt{10} \) because \( 2 \times 5 = 10 \) remains under the radical.
Let's look at another example to clarify:
| Example | Prime Factorization | Simplified Form |
| \( \sqrt{50} \) | \( 50 = 2 \times 5^2 \) | \( \sqrt{2 \times 5^2} = 5\sqrt{2} \) |
| \( \sqrt{72} \) | \( 72 = 2^3 \times 3^2 \) | \( \sqrt{2^3 \times 3^2} = 6\sqrt{2} \) |
| \( \sqrt{32} \) | \( 32 = 2^5 \) | \( \sqrt{2^5} = 4\sqrt{2} \) |
By following these steps, you can simplify any square root. This is especially useful in algebra, geometry, and higher-level math, where simplified forms make further calculations easier and more intuitive.
Remember, the key to simplifying square roots is recognizing patterns in prime factorization and being methodical in pairing and simplifying the factors. With practice, these steps become second nature, allowing you to handle complex radicals with confidence.
Step-by-Step Process to Simplify the Square Root of 90
Simplifying the square root of 90 involves breaking down the number into its simplest radical form. This process helps in reducing the expression to a more manageable and understandable form. Here’s a detailed, step-by-step guide to simplify \( \sqrt{90} \).
- Find the Prime Factorization of 90:
Start by identifying the prime factors of 90. Prime factorization is the process of breaking down a number into the product of its prime numbers. For 90, the prime factors are:
- 90 is divisible by 2: \( 90 \div 2 = 45 \)
- 45 is divisible by 3: \( 45 \div 3 = 15 \)
- 15 is divisible by 3 again: \( 15 \div 3 = 5 \)
- 5 is a prime number.
So, the prime factorization of 90 is \( 2 \times 3 \times 3 \times 5 \) or \( 2 \times 3^2 \times 5 \).
- Express 90 as a Product of Its Prime Factors:
Rewrite 90 under the square root as a product of its prime factors:
\( \sqrt{90} = \sqrt{2 \times 3^2 \times 5} \)
- Pair the Prime Factors:
Group the identical prime factors in pairs under the square root. For \( \sqrt{90} \), the pairs are:
\( 3^2 = 3 \times 3 \)
Since \( 3^2 \) is a perfect square, it can be taken outside the radical:
\( \sqrt{2 \times 3^2 \times 5} = 3\sqrt{2 \times 5} \)
- Simplify the Remaining Radical:
Multiply the factors left inside the radical:
\( 2 \times 5 = 10 \)
Thus, the expression simplifies to:
\( 3\sqrt{10} \)
Therefore, the simplified radical form of \( \sqrt{90} \) is \( 3\sqrt{10} \). Here’s a summary in tabular form:
| Step | Expression | Explanation |
| 1 | \( \sqrt{90} \) | Original square root to simplify. |
| 2 | \( \sqrt{2 \times 3^2 \times 5} \) | Prime factorize 90. |
| 3 | \( 3\sqrt{2 \times 5} \) | Simplify by taking the pair \( 3^2 \) outside the radical. |
| 4 | \( 3\sqrt{10} \) | Multiply remaining factors under the radical. |
By following these steps, you can simplify the square root of 90 to \( 3\sqrt{10} \), making it easier to use in further calculations.
Prime Factorization Method to Simplify √90
The prime factorization method is a systematic approach to simplify the square root of a number. By breaking down the number into its prime factors, we can identify and extract perfect squares, making the expression simpler. Let’s apply this method to simplify \( \sqrt{90} \).
- Find the Prime Factors of 90:
Prime factorization involves expressing a number as a product of its prime numbers. For 90, the process is as follows:
- 90 is even and divisible by 2: \( 90 \div 2 = 45 \).
- 45 is divisible by 3: \( 45 \div 3 = 15 \).
- 15 is also divisible by 3: \( 15 \div 3 = 5 \).
- 5 is a prime number.
So, the prime factors of 90 are \( 2 \times 3^2 \times 5 \).
- Write the Square Root with the Prime Factors:
Substitute the prime factors back into the square root:
\( \sqrt{90} = \sqrt{2 \times 3^2 \times 5} \)
- Identify and Extract Perfect Squares:
Look for any pairs of prime factors that form perfect squares. In our example, \( 3^2 \) is a perfect square:
\( \sqrt{2 \times 3^2 \times 5} \)
Since \( 3^2 \) equals 9, which is a perfect square, it can be taken out of the square root as a single 3:
\( 3\sqrt{2 \times 5} \)
- Multiply Remaining Factors under the Radical:
Multiply the factors left inside the square root. Here, \( 2 \times 5 = 10 \):
\( 3\sqrt{10} \)
Thus, the simplified radical form of \( \sqrt{90} \) is \( 3\sqrt{10} \).
| Step | Expression | Description |
| 1 | \( \sqrt{90} \) | Start with the square root of 90. |
| 2 | \( \sqrt{2 \times 3^2 \times 5} \) | Write 90 as the product of its prime factors. |
| 3 | \( 3\sqrt{2 \times 5} \) | Extract the perfect square \( 3^2 \) as 3 outside the radical. |
| 4 | \( 3\sqrt{10} \) | Multiply remaining factors under the radical. |
Using the prime factorization method allows for an efficient way to simplify square roots, particularly when dealing with larger numbers or those that aren't immediately obvious as perfect squares.

Using the Perfect Square Factors to Simplify √90
Simplifying the square root of 90 by using perfect square factors involves breaking down the number into factors where at least one is a perfect square. This method is straightforward and particularly useful for quickly simplifying square roots. Here’s how you can simplify \( \sqrt{90} \) using perfect square factors.
- Identify the Factors of 90:
First, list the factors of 90. We are looking for pairs where one is a perfect square:
- 1 and 90
- 2 and 45
- 3 and 30
- 5 and 18
- 9 and 10
Among these, 9 is a perfect square (\( 9 = 3^2 \)). So, we can pair 9 with 10.
- Rewrite 90 as a Product of a Perfect Square and Another Factor:
Express 90 in terms of its perfect square factor:
\( 90 = 9 \times 10 \)
- Use the Product Property of Square Roots:
The product property of square roots states that \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \). Apply this property to our factors:
\( \sqrt{90} = \sqrt{9 \times 10} = \sqrt{9} \times \sqrt{10} \)
- Simplify the Perfect Square:
Since 9 is a perfect square, \( \sqrt{9} = 3 \). Simplify \( \sqrt{9} \) outside the radical:
\( \sqrt{90} = 3 \times \sqrt{10} \)
Thus, the simplified form of \( \sqrt{90} \) using perfect square factors is \( 3\sqrt{10} \).
To visualize this process, let’s look at it in a tabular form:
| Step | Expression | Description |
| 1 | \( \sqrt{90} \) | Start with the square root of 90. |
| 2 | \( \sqrt{9 \times 10} \) | Rewrite 90 as a product of its perfect square factor 9 and another factor 10. |
| 3 | \( \sqrt{9} \times \sqrt{10} \) | Apply the product property of square roots. |
| 4 | \( 3\sqrt{10} \) | Simplify the perfect square \( \sqrt{9} \) to 3 outside the radical. |
Using the perfect square factor method simplifies the square root of non-perfect squares by leveraging the properties of square roots and identifying factors that are easier to handle. This method is effective for numbers like 90, where a perfect square factor exists.
Expressing √90 in Simplified Radical Form
To express the square root of 90 in simplified radical form, we need to follow these steps:
- First, find the prime factorization of 90.
- 90 can be factored into 9 and 10, i.e., 90 = 9 × 10.
- Next, factor 9 and 10 into their prime factors: 9 = 3 × 3 and 10 = 2 × 5.
- So, 90 = 3 × 3 × 2 × 5.
- Group the prime factors into pairs of identical factors.
- The prime factors of 90 are: 3, 3, 2, 5.
- Here, we can pair one set of 3s: (3 × 3) × 2 × 5.
- Take the square root of each pair of identical factors and move them outside the radical.
- The pair of 3s can be taken out of the radical as a single 3.
- What remains inside the radical are the unpaired factors: 2 and 5.
- Multiply the factors outside and inside the radical.
- Outside the radical: 3.
- Inside the radical: 2 × 5 = 10.
- Thus, √90 simplifies to 3√10.
Therefore, the simplified radical form of √90 is:
Comparison with Decimal Form: √90 ≈ 9.49
When simplifying the square root of 90, we find that:
This simplified form, 3√10, can be compared to its decimal approximation. Here’s a step-by-step process to understand the comparison:
- First, calculate the decimal value of √10.
- The approximate value of √10 is 3.162.
- Next, multiply this value by 3 (since we simplified √90 to 3√10).
- 3 × 3.162 = 9.486.
- Round the result to two decimal places for simplicity.
- 9.486 rounds to approximately 9.49.
Therefore, we can say:
This demonstrates that the simplified radical form 3√10 is equivalent to the decimal value approximately 9.49, providing a clear comparison between the two representations.
Applications and Examples of Simplified Radicals
Simplified radicals are frequently used in various mathematical and practical applications. Here are some common uses and examples:
1. Geometry and Measurement
Simplified radicals often appear in geometric calculations, such as finding the lengths of sides in right triangles, the diagonals of squares, and other shapes. For example, the diagonal \(d\) of a square with side length \(s\) can be found using the Pythagorean theorem:
\[
d = \sqrt{s^2 + s^2} = \sqrt{2s^2} = s\sqrt{2}
\]
2. Simplifying Expressions
Simplifying expressions involving radicals makes them easier to work with, particularly when adding, subtracting, or multiplying them. For example, combining like terms:
\[
\sqrt{12} + 3\sqrt{3} = 2\sqrt{3} + 3\sqrt{3} = 5\sqrt{3}
\]
3. Solving Equations
When solving algebraic equations, simplified radicals can help find exact solutions. For example, solving \(x^2 = 90\) gives:
\[
x = \pm\sqrt{90} = \pm3\sqrt{10}
\]
4. Real-life Problems
Radicals appear in real-life problems involving areas, volumes, and other measurements. For instance, if the area of a square garden is 90 square yards, the side length \(s\) of the garden is:
\[
s = \sqrt{90} = 3\sqrt{10} \approx 9.49 \text{ yards}
\]
The perimeter of the garden is then:
\[
4s = 4 \times 9.49 = 37.96 \text{ yards}
\]
5. Advanced Mathematical Concepts
In higher mathematics, simplified radicals are used in calculus, trigonometry, and other fields to simplify and solve complex problems. For instance, in calculus, radicals are used to find derivatives and integrals of functions involving roots.
Example Problems
- Find the simplified form of \(\sqrt{72}\):
\[
\sqrt{72} = \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} = 6\sqrt{2}
\] - Simplify \(\sqrt{50} + \sqrt{18}\):
\[
\sqrt{50} = 5\sqrt{2}, \quad \sqrt{18} = 3\sqrt{2}
\]\[
\sqrt{50} + \sqrt{18} = 5\sqrt{2} + 3\sqrt{2} = 8\sqrt{2}
\]
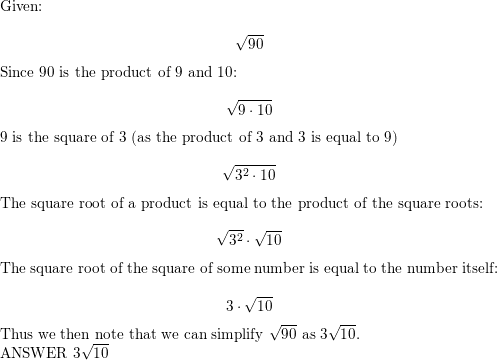
Common Mistakes to Avoid When Simplifying Radicals
Simplifying radicals can be challenging, but avoiding common mistakes can make the process easier and more accurate. Here are some key points to keep in mind:
- Incorrect Prime Factorization: Ensure that you correctly perform the prime factorization of the number under the radical. For example, the prime factorization of 90 is \( 2 \times 3^2 \times 5 \).
- Forgetting to Extract All Square Factors: Make sure to extract all possible square factors from under the radical. For \(\sqrt{90}\), the correct simplification involves recognizing that \( 3^2 \) is a square factor, leading to \( 3\sqrt{10} \).
- Leaving the Radical in an Unsimplified Form: Always simplify the radical to its simplest form. For example, don’t leave \(\sqrt{90}\) as it is when it can be simplified to \( 3\sqrt{10} \).
- Incorrect Multiplication of Factors: Be careful when multiplying factors outside the radical. Ensure that you only multiply terms correctly, such as \( 3 \times \sqrt{10} \) remains \( 3\sqrt{10} \) and not \(\sqrt{30}\).
- Misinterpreting the Radical Rules: Understand the basic rules of radicals, such as \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \). Misapplying these rules can lead to incorrect simplifications.
Here’s a step-by-step guide to avoid these mistakes when simplifying \(\sqrt{90}\):
- Perform the prime factorization of 90: \( 90 = 2 \times 3^2 \times 5 \).
- Identify and extract the square factors: \( \sqrt{90} = \sqrt{2 \times 3^2 \times 5} \).
- Rewrite the expression to highlight the square factor: \( \sqrt{2 \times 3^2 \times 5} = \sqrt{3^2} \times \sqrt{2 \times 5} \).
- Simplify the square root of the square factor: \( \sqrt{3^2} = 3 \).
- Combine the simplified factor with the remaining radical: \( 3\sqrt{10} \).
By following these steps and being aware of these common mistakes, you can simplify radicals accurately and efficiently.
Practice Problems for Simplifying Square Roots
Practicing the simplification of square roots is essential to mastering the concept. Below are several practice problems that will help you reinforce your understanding of simplifying square roots using different methods.
- Simplify the following square roots by finding the largest perfect square factor:
- \(\sqrt{72}\)
- \(\sqrt{180}\)
- \(\sqrt{200}\)
- Use the product property of square roots to simplify:
- \(\sqrt{50}\)
- \(\sqrt{98}\)
- \(\sqrt{125}\)
- Simplify the square roots of the following expressions:
- \(\sqrt{32}\)
- \(\sqrt{75}\)
- \(\sqrt{147}\)
- Simplify the square roots involving variables:
- \(\sqrt{50x^2}\)
- \(\sqrt{72y^4}\)
- \(\sqrt{18z^6}\)
Here are some worked examples to guide you:
| \(\sqrt{72}\) |
|
| \(\sqrt{180}\) |
|
| \(\sqrt{50}\) |
|
Try solving the above problems on your own and then check your answers with the provided solutions. Consistent practice will improve your ability to simplify square roots efficiently and accurately.
Further Resources and Reading on Radical Expressions
Understanding and simplifying radical expressions, such as the square root of 90, is a fundamental skill in algebra and higher mathematics. To deepen your knowledge and find additional practice, consider exploring the following resources:
- Khan Academy: Offers comprehensive lessons and practice problems on simplifying radicals, including video tutorials and interactive exercises. Visit for more.
- Mathway: A versatile tool that not only provides step-by-step solutions to algebraic problems but also explains the process of simplifying square roots. Explore more at .
- Cuemath: Provides detailed articles and solved examples related to the square root of 90 and other radical expressions. Check out their article on for a thorough understanding.
- Wolfram Alpha: An excellent computational engine that can solve and simplify radicals, offering both exact and decimal forms. Visit for advanced calculations.
- Interactive Math Websites: Sites like Purplemath and Math is Fun offer explanations and interactive problems to practice simplifying square roots and other radical expressions. Find more resources at and .
Additionally, numerous textbooks and online courses cover radical expressions in depth. Whether you are a student seeking to improve your skills or an educator looking for teaching resources, these tools and websites provide valuable information and practice opportunities.
Frequently Asked Questions about Simplifying Radicals
Understanding how to simplify radicals can be challenging. Below are some frequently asked questions to help clarify common doubts and improve your understanding.
-
Q: What is a radical?
A: A radical is an expression that includes a root symbol (√). For example, √90 is a radical expression.
-
Q: How do you simplify the square root of 90?
A: To simplify √90, you break it down into prime factors and look for perfect squares:
- Prime factorize 90: 90 = 2 × 3² × 5
- Identify the perfect squares: 3²
- Rewrite the expression: √90 = √(3² × 2 × 5) = 3√10
-
Q: Why do we need to simplify radicals?
A: Simplifying radicals makes them easier to work with in algebraic expressions and can reveal properties of the number that are not immediately obvious.
-
Q: Can all square roots be simplified?
A: Not all square roots can be simplified to remove the radical entirely, but many can be reduced to a simpler form.
-
Q: What are some common mistakes to avoid when simplifying radicals?
A: Common mistakes include:
- Forgetting to simplify completely by not finding all perfect square factors.
- Incorrectly assuming that the square root of a product is the product of the square roots.
- Not checking if the result can be simplified further.
-
Q: Can the square root of a negative number be simplified?A: The square root of a negative number is not a real number but can be expressed using imaginary numbers. For example, √(-1) = i.
-
Q: How can I practice simplifying radicals?
A: Practice problems and worksheets are available online, and many math textbooks include exercises on this topic. Use resources like Khan Academy and Math Warehouse for guided practice.

Conclusion: Mastering the Simplification of √90
Mastering the simplification of square roots, such as √90, involves understanding key mathematical concepts and applying them systematically. Here's a step-by-step recap of the process:
- Identify the perfect square factors: √90 can be expressed as √(9×10).
- Apply the product rule for radicals: √90 = √9 × √10.
- Simplify the square root of the perfect square: √9 = 3.
- Combine the simplified terms: 3√10.
Thus, the simplified radical form of √90 is 3√10.
Through consistent practice and by avoiding common mistakes, such as failing to recognize perfect square factors or incorrectly combining unlike radicals, one can achieve proficiency in simplifying radicals.
Understanding the difference between the simplified radical form and its decimal approximation is also crucial. While the exact simplified form of √90 is 3√10, its decimal form is approximately 9.49. This distinction is important for applications requiring precision.
By mastering these steps and concepts, you can confidently simplify a wide range of square roots and apply this knowledge in various mathematical contexts.
Hướng dẫn cách đơn giản hóa căn bậc hai của 90 trong video này sẽ giúp bạn nắm vững các bước cơ bản và áp dụng dễ dàng vào bài toán.
Cách Đơn Giản Hóa Căn Bậc Hai của 90: sqrt(90)
READ MORE:
Căn bậc hai của 90 được đơn giản hóa