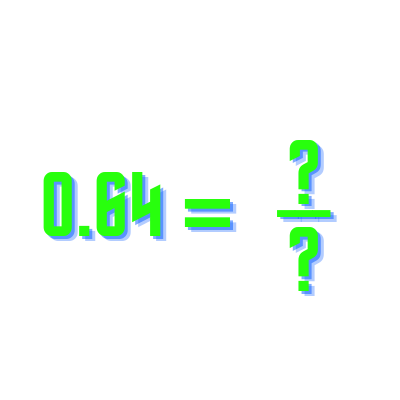Topic what is the square root of 100: Curious about what the square root of 100 is? You’re in the right place! Understanding the square root of this perfect square is easier than you might think. Read on to find out the straightforward answer and explore the fascinating concepts behind square roots.
Table of Content
- Square Root of 100
- Introduction to Square Roots
- Understanding the Concept of Square Roots
- Mathematical Definition of Square Roots
- Square Root of 100: Basic Explanation
- Calculation of Square Root of 100
- Properties of the Square Root of 100
- Square Roots in Real Life Applications
- Historical Background of Square Roots
- Visualizing Square Roots
- Common Misconceptions about Square Roots
- Advanced Concepts Related to Square Roots
- Using Technology to Calculate Square Roots
- Practice Problems and Solutions
- Conclusion and Further Reading
- YOUTUBE: Tìm hiểu về căn bậc hai của 100 trong video này để thu hút người xem và cải thiện kiến thức của bạn.
Square Root of 100
The square root of 100 is a fundamental mathematical concept that is often encountered in various calculations and problem-solving scenarios. Below is a detailed explanation and various methods to calculate the square root of 100.
Definition
The square root of a number is a value that, when multiplied by itself, gives the original number. The square root of 100 can be written as:
$$ \sqrt{100} = 10 $$
Methods to Calculate the Square Root of 100
-
Prime Factorization
Using prime factorization, we can express 100 as:
$$ 100 = 2^2 \times 5^2 $$
Taking the square root of both sides, we get:
$$ \sqrt{100} = \sqrt{2^2 \times 5^2} = 2 \times 5 = 10 $$
-
Long Division Method
- Pair the digits of 100 from right to left (100).
- Find a number whose square is less than or equal to 100 (10 × 10 = 100).
- Since 10 × 10 = 100, we find that the square root of 100 is 10.
-
Using a Calculator
Most calculators have a square root function. Simply enter 100 and press the square root button (√) to get:
-
Using Exponents
The square root can also be expressed using exponents:
$$ \sqrt{100} = 100^{1/2} = 10 $$
Properties
- 100 is a perfect square since it can be expressed as \(10^2\).
- The square root of 100 is a rational number.
- It has both positive and negative values: \( \pm 10 \).
Applications
- Used in geometry to calculate the sides of squares.
- Commonly used in various algebraic equations.
- Useful in real-life situations like determining areas and lengths.
Table of Square Roots for Comparison
| Number | Square Root |
|---|---|
| 64 | 8 |
| 81 | 9 |
| 100 | 10 |
| 121 | 11 |

READ MORE:
Introduction to Square Roots
Square roots are fundamental concepts in mathematics, representing a number that, when multiplied by itself, gives the original number. For example, the square root of 100 is a number \( x \) such that \( x^2 = 100 \).
Here's a step-by-step understanding of square roots:
- Definition: The square root of a number \( n \) is a value that, when squared, equals \( n \). This is represented as \( \sqrt{n} \).
- Perfect Squares: Numbers like 100, 81, and 64 are perfect squares because they are squares of integers (10, 9, and 8, respectively).
- Calculating Square Roots: For perfect squares, the square root can be found easily. For instance, \( \sqrt{100} = 10 \) because \( 10 \times 10 = 100 \).
- Properties:
- Square roots of positive numbers are always non-negative.
- The square root function is the inverse of squaring a number.
To further illustrate, let's look at a simple table of perfect squares and their roots:
| Number | Square Root |
| 100 | 10 |
| 81 | 9 |
| 64 | 8 |
| 49 | 7 |
| 36 | 6 |
Understanding square roots is crucial for various mathematical applications, including algebra, geometry, and more advanced fields. Embrace this concept, and you’ll find it simplifies many mathematical problems.
Understanding the Concept of Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. It is a fundamental concept in mathematics, particularly in algebra and geometry. To understand square roots, let's break down the concept step by step:
1. Definition: The square root of a number x is a number y such that \( y^2 = x \). The square root is usually denoted by the radical symbol √.
2. Positive and Negative Roots: Every positive number has two square roots: a positive root and a negative root. For example, the square roots of 100 are 10 and -10, since \( 10^2 = 100 \) and \( (-10)^2 = 100 \).
3. Principal Square Root: By convention, the principal square root is the non-negative root. When we refer to the square root of a number, we typically mean the principal square root. For instance, √100 = 10.
Examples of Square Roots
√16 = 4, because \( 4^2 = 16 \)√25 = 5, because \( 5^2 = 25 \)√81 = 9, because \( 9^2 = 81 \)
Properties of Square Roots
- Non-negative: The principal square root of a non-negative number is always non-negative.
- Product Property: The square root of a product is the product of the square roots:
√(ab) = √a × √b. - Quotient Property: The square root of a quotient is the quotient of the square roots:
√(a/b) = √a / √b.
Visual Representation
Square roots can also be visualized geometrically. For example, the square root of 100 can be represented as the side length of a square with an area of 100 square units.
Consider the following table of perfect squares and their roots:
| Number | Square Root |
|---|---|
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
| 36 | 6 |
| 49 | 7 |
| 64 | 8 |
| 81 | 9 |
| 100 | 10 |
Understanding these fundamental properties and visual representations helps in grasping the concept of square roots, making it easier to apply them in various mathematical problems and real-life scenarios.
Mathematical Definition of Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. In mathematical terms, if \( x \) is the square root of \( y \), then \( x^2 = y \).
For example, the square root of 100 is a number \( x \) such that \( x^2 = 100 \). The number 10 is the square root of 100 because \( 10^2 = 100 \).
There are several key concepts associated with square roots:
- Radical Symbol (√): The symbol used to denote the square root.
- Radicand: The number under the radical symbol. For √100, the radicand is 100.
- Principal Square Root: The non-negative square root of a number. For 100, the principal square root is 10.
- Negative Square Root: The negative counterpart of the principal square root. For 100, it is -10.
Using mathematical notation, the square roots of 100 can be represented as:
\[
\sqrt{100} = 10 \quad \text{and} \quad -\sqrt{100} = -10
\]
The concept of square roots can be extended to complex numbers, where the square root of a negative number involves the imaginary unit \( i \), defined as \( i = \sqrt{-1} \). For instance, the square root of -100 is expressed as:
\[
\sqrt{-100} = 10i
\]
Here, \( 10i \) is the imaginary square root of -100.
In summary, the square root function provides a way to determine a number that, when squared, returns the original value. This concept is fundamental in various mathematical applications, from solving quadratic equations to analyzing geometrical properties.
Square Root of 100: Basic Explanation
The square root of a number is a value that, when multiplied by itself, gives the original number. In mathematical terms, if \( y \) is the square root of \( x \), then \( y^2 = x \). For the number 100, the square root is 10 because \( 10 \times 10 = 100 \).
Here are some key points to understand the concept better:
- The square root symbol is \( \sqrt{} \).
- When we write \( \sqrt{100} \), we are asking for a number that, when squared, equals 100.
- The square root of 100 is 10 because \( 10^2 = 100 \).
- Every positive number has two square roots: a positive and a negative one. Thus, the square roots of 100 are \( \pm 10 \).
Mathematically, this can be expressed as:
\[
\sqrt{100} = \pm 10
\]
Steps to Calculate the Square Root of 100
Here’s a simple step-by-step explanation:
- Identify the number for which you need to find the square root. In this case, it's 100.
- Find a number which, when multiplied by itself, equals 100. By trial or knowledge of basic squares, we know \( 10 \times 10 = 100 \).
- Conclude that 10 is the square root of 100.
Properties of the Square Root of 100
- It is a perfect square, meaning it has an integer as its square root.
- The square root of 100 is rational, as it can be expressed as an integer (10).
- It’s positive square root is referred to as the principal square root, which is 10.
Visual Representation
To visualize, think of a square with an area of 100 square units. Each side of this square will be 10 units long because \( 10 \times 10 = 100 \).
Conclusion
Understanding the square root of 100 helps in grasping the fundamental concepts of square roots. The square root of 100 is straightforward because it is a perfect square. Knowing that \( \sqrt{100} = \pm 10 \) is useful in various mathematical and real-life applications.

Calculation of Square Root of 100
The square root of 100 can be calculated using various methods such as prime factorization and the long division method. Here, we'll explain both methods in detail.
Prime Factorization Method
Prime factorization involves breaking down 100 into its prime factors and then using these factors to find the square root.
- Find the prime factors of 100:
100 = 2 × 2 × 5 × 5
- Group the factors into pairs of the same numbers:
(2 × 2) and (5 × 5)
- Take one number from each pair:
2 and 5
- Multiply these numbers to get the square root:
\(\sqrt{100} = 2 \times 5 = 10\)
Long Division Method
The long division method is another way to find the square root of 100. Here are the steps:
- Pair the digits of the number starting from the decimal point (if any) to the left:
100 is already a pair of digits.
- Find a number whose square is less than or equal to the first pair:
The largest number whose square is less than or equal to 100 is 10 (since \(10 \times 10 = 100\)).
- Place the quotient above the number:
Quotient is 10.
- Subtract the square of the quotient from the original number and bring down the next pair of digits (if any):
Since \(10 \times 10 = 100\) and there are no more digits to bring down, the calculation is complete.
Thus, the square root of 100 using the long division method is also 10.
Summary
Both the prime factorization and long division methods yield the same result:
\[\sqrt{100} = 10\]
Therefore, the square root of 100 is 10.
Properties of the Square Root of 100
The square root of 100 is an important mathematical concept with several noteworthy properties. Understanding these properties helps in various mathematical and real-world applications.
- Value: The square root of 100 is 10. This is because \(10 \times 10 = 100\).
- Positive and Negative Roots: While the principal square root of 100 is 10, it's important to note that -10 is also a square root of 100 because \((-10) \times (-10) = 100\).
- Rational Number: The square root of 100 is a rational number since it can be expressed as a fraction, specifically \( \frac{10}{1} \).
- Perfect Square: 100 is a perfect square, which means its square root is an integer. This property simplifies many calculations and applications.
- Even Number: The square root of 100 is an even number, which is useful in certain algebraic and geometric contexts.
- Multiplicative Property: The square root of a product can be expressed as the product of the square roots. For example, \( \sqrt{100} = \sqrt{25 \times 4} = \sqrt{25} \times \sqrt{4} = 5 \times 2 = 10 \).
- Exponential Form: In exponential notation, the square root of 100 can be written as \( 100^{0.5} \) or \( 10^1 \).
- Logarithmic Relation: The square root of 100 can also be related to logarithms. For example, if \( \log_{10}(100) = 2 \), then \( \sqrt{100} = 10^{\frac{2}{2}} = 10 \).
These properties highlight the significance and versatility of the square root of 100 in various mathematical domains.
Square Roots in Real Life Applications
The concept of square roots, including the square root of 100, is frequently applied in various real-life scenarios. Here are some notable examples:
- Geometry and Measurement: Square roots are essential in geometry for calculating the length of the sides of squares and right triangles. For instance, if the area of a square is 100 square units, the length of each side is the square root of 100, which is 10 units.
- Architecture and Construction: Architects and engineers use square roots to determine dimensions and ensure structural integrity. For example, in designing a square-shaped garden or plaza with an area of 100 square meters, each side would measure 10 meters.
- Physics: In physics, square roots are used to solve equations involving areas and distances. For example, if a sphere has a surface area of 400π square units, its radius can be found using the formula \(A = 4πr^2\). Solving for \(r\) involves taking the square root of 100, giving a radius of 10 units.
- Finance: Square roots are applied in finance to calculate volatility and risk. The standard deviation, a measure of market volatility, is often derived from the square root of the variance.
- Technology: In computer graphics, algorithms often use square roots to calculate distances between points in a 2D or 3D space. This is crucial for rendering images and simulations accurately.
- Gardening: A practical example in gardening is determining the layout of plants. For a gardener with 100 plants who wants to arrange them in a square formation, each row would contain 10 plants, as the square root of 100 is 10.
These examples illustrate how understanding and using square roots can simplify complex problems and provide practical solutions in everyday life.
Historical Background of Square Roots
The concept of square roots has a rich and varied history, stretching back to ancient civilizations and progressing through significant mathematical advancements over the centuries.
- Ancient Civilizations: The Babylonians, around 2000 BCE, were among the first to develop methods for approximating square roots, recorded on clay tablets. Their method involved iterative approaches to get closer to the true value.
- Greek Contributions: The Greeks, particularly through the work of Pythagoras and later Euclid, explored square roots in the context of geometry. They understood the square root of a number as the side length of a square with that area.
- Indian Mathematicians: In the 5th century, Indian mathematician Aryabhata provided algorithms for extracting square roots and used these methods in astronomical calculations.
- Islamic Golden Age: Mathematicians like Al-Khwarizmi in the 9th century further developed methods for solving quadratic equations, which inherently involved finding square roots. Al-Khwarizmi’s works were later translated into Latin, significantly influencing European mathematics.
- Medieval Europe: The 12th-century mathematician Leonardo of Pisa, known as Fibonacci, introduced Arabic numerals and algebraic techniques, including methods for finding square roots, to Europe in his book "Liber Abaci".
- Renaissance Advancements: During the Renaissance, mathematicians such as Girolamo Cardano and Niccolò Tartaglia made substantial progress in algebra, which included solving cubic and quartic equations that required an understanding of square roots.
- Modern Era: The development of calculus and numerical methods in the 17th and 18th centuries by Newton and others allowed for more precise calculations of square roots. The introduction of algorithms like the Newton-Raphson method provided efficient means to approximate square roots.
Today, the understanding and computation of square roots are fundamental in mathematics and its applications, benefiting from the cumulative knowledge and techniques developed over millennia.

Visualizing Square Roots
Visualizing square roots can be a powerful way to understand their properties and applications. Below are some methods and examples to help visualize the square root of 100 and square roots in general:
Number Line Representation
One of the simplest ways to visualize the square root of a number is on a number line:
- Place the number whose square root you want to find on the number line. For example, 100.
- The square root of 100, which is 10, will be the point that, when squared, gives the original number (100).
- On the number line, you can mark points at 0, 10, and 100 to illustrate this.
Geometric Interpretation
Square roots can also be visualized using geometric shapes:
- Consider a square with an area of 100 square units. The side length of this square is the square root of 100.
- Since the area of a square is given by side length squared, we solve for the side length by taking the square root: \( \sqrt{100} = 10 \).
- Thus, each side of the square measures 10 units.
Graphical Representation
Graphing the function \( y = \sqrt{x} \) can provide another visual way to understand square roots:
- Plot the function \( y = \sqrt{x} \) on a coordinate plane.
- The point (100, 10) will lie on this curve, illustrating that the square root of 100 is 10.
Interactive Tools
Using interactive tools and software can enhance the visualization of square roots:
- Graphing calculators and online tools allow you to input different values and see their square roots instantly.
- Many educational websites provide interactive graphs and animations to help visualize square roots.
Example Visualization in Real Life
Let's take a practical example to visualize the square root of 100:
- Imagine a garden plot with an area of 100 square meters. To find the length of each side if it is square-shaped, we calculate the square root of 100.
- The length of each side will be 10 meters, as \( \sqrt{100} = 10 \).
Tabular Representation
A table can help compare square roots of different numbers for better understanding:
| Number | Square Root |
|---|---|
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
| 100 | 10 |
By using these different methods and examples, we can gain a deeper understanding and visualization of square roots, making the concept more intuitive and easier to grasp.
Common Misconceptions about Square Roots
Square roots are a fundamental concept in mathematics, but several misconceptions can lead to confusion. Below are some common misconceptions about square roots and clarifications to help understand them better:
- Misconception 1: The square root of a number always has two values
Many students believe that \(\sqrt{x}\) always yields two values: a positive and a negative result. However, the principal square root function, denoted as \(\sqrt{x}\), only returns the non-negative root. For example, \(\sqrt{100} = 10\), not \(\pm 10\). The notation \(\pm\) is used when solving equations like \(x^2 = 100\) to account for both possible solutions, \(x = 10\) and \(x = -10\).
- Misconception 2: \(\sqrt{x+y} = \sqrt{x} + \sqrt{y}\)
This is a common error due to misunderstanding how square roots work. In reality, \(\sqrt{x + y} \neq \sqrt{x} + \sqrt{y}\). For instance, \(\sqrt{4 + 9} = \sqrt{13}\), which is not equal to \(\sqrt{4} + \sqrt{9} = 2 + 3 = 5\). Such additive assumptions do not hold true for roots.
- Misconception 3: The square root function is the inverse of the square function for all real numbers
While the square root function is the inverse of the square function, this is only true for non-negative numbers. The square function \(x^2\) has a domain of all real numbers, but the square root function \(\sqrt{x}\) is only defined for \(x \geq 0\) in the set of real numbers. Thus, \(\sqrt{x^2} = |x|\), not simply \(x\), to account for the absolute value.
- Misconception 4: Errors in simplifying expressions involving square roots
Another frequent mistake involves the incorrect simplification of expressions. For example, students might incorrectly simplify \(\sqrt{x^2 + y^2}\) as \(\sqrt{x^2} + \sqrt{y^2}\), which is incorrect. Proper understanding requires recognizing that such simplifications are invalid unless specific conditions are met.
- Misconception 5: Solving equations and the square root step
When solving equations such as \(x^2 = 25\), students often mistakenly write \(x = \sqrt{25}\), omitting the negative solution. The correct approach is to write \(x = \pm \sqrt{25}\) to include both \(x = 5\) and \(x = -5\).
By understanding these misconceptions and the correct principles, one can avoid common errors and have a better grasp of square roots and their applications.
Advanced Concepts Related to Square Roots
The study of square roots extends beyond basic arithmetic into more complex mathematical areas. Below are some advanced concepts related to square roots:
- Complex Numbers: The square root function can be extended to complex numbers. For a complex number \( z = a + bi \), its square roots are also complex numbers. If \( z \) is not zero, it has two square roots given by:
\(\pm \sqrt{r} \left( \cos \frac{\theta}{2} + i \sin \frac{\theta}{2} \right)\)
where \( r \) is the modulus and \( \theta \) is the argument of \( z \). - Matrix Square Roots: In linear algebra, a square root of a matrix \( A \) is another matrix \( B \) such that \( B^2 = A \). Not all matrices have square roots, but those that do can have multiple square roots.
- Function Spaces: In functional analysis, square roots can be defined for operators on function spaces. For instance, if \( T \) is a positive definite operator, there exists an operator \( S \) such that \( S^2 = T \).
- Fractional Exponents: The square root can be expressed using fractional exponents. For any positive real number \( x \):
\[ \sqrt{x} = x^{\frac{1}{2}} \] This notation generalizes to other roots, where \( x^{\frac{m}{n}} \) represents the \( n \)-th root of \( x \) raised to the power of \( m \). - Newton's Method: An iterative numerical method for finding successively better approximations to the roots (or zeroes) of a real-valued function. To find the square root of \( S \), one can use:
\[ x_{n+1} = \frac{1}{2} \left( x_n + \frac{S}{x_n} \right) \] Starting with an initial guess \( x_0 \). - Irrational and Transcendental Numbers: The square roots of non-square integers are irrational. Furthermore, certain algebraic numbers have square roots that are transcendental, meaning they are not roots of any non-zero polynomial equation with rational coefficients.
Using Technology to Calculate Square Roots
Calculating square roots has been greatly simplified with the advent of modern technology. Here are some of the methods and tools you can use:
1. Calculators
Most scientific and graphing calculators have a square root function, typically denoted by the symbol √. To find the square root of 100, you simply press the square root button followed by 100, and the result will be 10.
2. Computer Software
Various computer software programs, such as MATLAB, Mathematica, and Python, provide built-in functions to calculate square roots. For instance, in Python, you can use the math.sqrt() function:
import math
result = math.sqrt(100)
print(result) # Output: 10.03. Online Calculators
There are numerous online calculators available that can compute the square root of any number. Websites like Symbolab and Wolfram Alpha allow you to input your number and instantly get the square root along with additional information and visualizations.
4. Mobile Apps
Many mobile apps are designed for mathematical computations, including square roots. Apps like Microsoft Math Solver and Photomath not only calculate the square root but also show the steps involved in the calculation.
5. Spreadsheet Software
Programs like Microsoft Excel and Google Sheets have functions to calculate square roots. In Excel, you can use the =SQRT() function. For example, =SQRT(100) will return 10.
Example Using Excel
| Cell | Function | Result |
|---|---|---|
| A1 | 100 | |
| B1 | =SQRT(A1) | 10 |
Technology not only simplifies the calculation of square roots but also helps in understanding the concept through visual aids and step-by-step solutions, enhancing the learning experience.

Practice Problems and Solutions
Practicing square root problems can help solidify your understanding of the concept. Below are a series of problems with solutions to help you practice calculating square roots.
Basic Square Root Problems
-
Problem: Find the square root of 100.
Solution:
\[
\sqrt{100} = 10
\] -
Problem: Find the square root of 225.
Solution:
\[
\sqrt{225} = 15
\] -
Problem: Find the square root of 144.
Solution:
\[
\sqrt{144} = 12
\]
Intermediate Square Root Problems
-
Problem: Find the square root of 784.
Solution:
\[
\sqrt{784} = 28
\] -
Problem: Find the square root of 1,296.
Solution:
\[
\sqrt{1296} = 36
\] -
Problem: Find the square root of 2,500.
Solution:
\[
\sqrt{2500} = 50
\]
Advanced Square Root Problems
-
Problem: Find the square root of 10,000.
Solution:
\[
\sqrt{10000} = 100
\] -
Problem: Solve for \( x \) in the equation \( x^2 = 6400 \).
Solution:
\[
x = \pm \sqrt{6400} = \pm 80
\] -
Problem: Solve for \( y \) in the equation \( y^2 = 529 \).
Solution:
\[
y = \pm \sqrt{529} = \pm 23
\]
Real-World Application Problems
-
Problem: A square garden has an area of 400 square meters. Find the length of one side of the garden.
Solution:
\[
\text{Side length} = \sqrt{400} = 20 \text{ meters}
\] -
Problem: The area of a square painting is 625 square inches. What is the length of one side of the painting?
Solution:
\[
\text{Side length} = \sqrt{625} = 25 \text{ inches}
\] -
Problem: If a square field has an area of 2,025 square feet, find the length of one side of the field.
Solution:
\[
\text{Side length} = \sqrt{2025} = 45 \text{ feet}
\]
Conclusion and Further Reading
The square root of 100 is a fundamental mathematical concept with broad implications and applications in various fields. It highlights the importance of understanding basic arithmetic operations and their inverses. In this guide, we have explored the definition, properties, calculation methods, and real-life applications of the square root of 100. We also delved into common misconceptions and advanced concepts related to square roots.
Understanding square roots is crucial not only for academic purposes but also for practical applications in science, engineering, and everyday problem-solving. The square root of 100, being a perfect square, offers a clear example of how these concepts can be applied and understood intuitively.
For those interested in further expanding their knowledge, here are some recommended readings and resources:
- Books:
- "The Joy of x: A Guided Tour of Math, from One to Infinity" by Steven Strogatz
- "Principles of Mathematics" by Bertrand Russell
- Online Resources:
- Software and Tools:
- Graphing calculators such as the TI-84 Plus
- Mathematical software like Wolfram Alpha
Continued practice and exploration of mathematical concepts can significantly enhance your understanding and application skills. Whether you are a student, educator, or enthusiast, there is always more to learn and discover in the fascinating world of mathematics.
Tìm hiểu về căn bậc hai của 100 trong video này để thu hút người xem và cải thiện kiến thức của bạn.
Căn bậc hai của 100
READ MORE:
Khám phá cách đơn giản hóa căn bậc hai của 100 trong video này để thu hút người xem và cải thiện kiến thức của bạn.
Cách Đơn Giản Hóa Căn Bậc Hai của 100: sqrt(100)