Topic simplify square root with variables: Discover how to simplify square roots with variables through clear, step-by-step instructions. Mastering this skill will enhance your algebra proficiency and make tackling complex mathematical problems easier. Dive in and learn the essential techniques to simplify square root expressions effortlessly, boosting your confidence and mathematical capabilities.
Table of Content
- Simplifying Square Roots with Variables
- Introduction
- Understanding Square Roots and Variables
- Basic Properties of Square Roots
- Factorizing Numbers and Variables
- Identifying and Grouping Pairs
- Moving Factors Outside the Square Root
- Multiplying Inside and Outside the Square Root
- Common Mistakes to Avoid
- Advanced Techniques for Complex Expressions
- Practice Problems and Solutions
- Applications in Algebra and Beyond
- Useful Formulas and Tips
- Conclusion
- YOUTUBE: Video hướng dẫn cách đơn giản hóa căn bậc hai với biến số một cách chi tiết và dễ hiểu. Phù hợp cho học sinh và người yêu thích toán học.
Simplifying Square Roots with Variables
Simplifying square roots with variables involves breaking down the expression into its simplest form. The process requires an understanding of basic algebraic principles and the properties of square roots.
Steps to Simplify Square Roots with Variables
- Factor the number inside the square root into its prime factors.
- Identify pairs of the same number/variable inside the square root.
- Move one number/variable from each pair outside the square root.
- Multiply the numbers/variables outside the square root.
- Multiply the numbers/variables left inside the square root.
Example Problems
Here are some example problems to illustrate the process:
-
Example 1: Simplify \( \sqrt{50x^2} \)
First, factorize the number inside the square root: \( 50 = 2 \times 5^2 \).
Identify pairs: \( \sqrt{50x^2} = \sqrt{2 \times 5^2 \times x^2} \).
Move one number/variable from each pair outside the square root: \( \sqrt{2 \times 5^2 \times x^2} = 5x\sqrt{2} \).
Thus, the simplified form is \( 5x\sqrt{2} \).
-
Example 2: Simplify \( \sqrt{72y^4} \)
First, factorize the number inside the square root: \( 72 = 2^3 \times 3^2 \).
Identify pairs: \( \sqrt{72y^4} = \sqrt{2^3 \times 3^2 \times y^4} \).
Move one number/variable from each pair outside the square root: \( \sqrt{2^3 \times 3^2 \times y^4} = 6y^2\sqrt{2} \).
Thus, the simplified form is \( 6y^2\sqrt{2} \).
Practice Problems
Try simplifying the following square roots with variables:
- Simplify \( \sqrt{32a^3} \)
- Simplify \( \sqrt{18b^5} \)
- Simplify \( \sqrt{45c^2} \)
- Simplify \( \sqrt{98d^4} \)
Remember to factorize the numbers, identify pairs, and simplify step by step. Happy learning!
Useful Formulas
| \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \) |
| \( \sqrt{a^2} = a \) |
| \( \sqrt{x^n} = x^{n/2} \) |

READ MORE:
Introduction
Simplifying square roots with variables is a fundamental skill in algebra that allows you to transform complex expressions into simpler, more manageable forms. This process is essential for solving equations, simplifying expressions, and understanding higher-level mathematics. By mastering this technique, you will improve your mathematical fluency and confidence.
The process of simplifying square roots with variables involves several key steps:
- Factor the expression inside the square root into its prime factors.
- Group the factors into pairs.
- Move one factor from each pair outside the square root.
- Multiply the factors outside and inside the square root separately.
Understanding and applying these steps correctly will help you simplify expressions like \( \sqrt{50x^2} \) to \( 5x\sqrt{2} \) and \( \sqrt{72y^4} \) to \( 6y^2\sqrt{2} \). Let's explore these steps in detail:
- Factor the expression: Break down the number and variable inside the square root into their prime factors.
- Group pairs: Identify and group pairs of the same factors.
- Move factors outside: For each pair, move one factor outside the square root.
- Multiply separately: Combine the factors outside and simplify the remaining expression inside the square root.
By following these steps, you can simplify complex square root expressions efficiently, making it easier to solve algebraic problems and gain deeper insights into mathematical concepts.
Understanding Square Roots and Variables
Square roots and variables are fundamental concepts in algebra, allowing for the simplification and solution of various mathematical expressions. To fully grasp how to simplify square roots with variables, it's essential to understand the properties of square roots and how variables interact within these expressions.
Properties of Square Roots
- Definition: The square root of a number \(a\) is a value \(b\) such that \(b^2 = a\). It is denoted as \( \sqrt{a} \).
- Product Property: \( \sqrt{ab} = \sqrt{a} \times \sqrt{b} \).
- Quotient Property: \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \).
- Power Property: \( \sqrt{a^2} = a \) for non-negative \(a\).
Understanding Variables in Square Roots
Variables within square roots follow the same properties as numerical values. When simplifying square roots that contain variables, treat the variables as factors that can be paired and simplified similarly to numbers.
Steps to Simplify Square Roots with Variables
- Factorization: Break down the number and variable into their prime factors.
- Example: \( \sqrt{50x^2} \rightarrow \sqrt{2 \times 5^2 \times x^2} \).
- Pairing Factors: Group identical factors into pairs.
- Example: \( \sqrt{2 \times 5^2 \times x^2} \rightarrow \sqrt{2} \times \sqrt{5^2} \times \sqrt{x^2} \).
- Extracting Pairs: Move one factor from each pair outside the square root.
- Example: \( \sqrt{2} \times \sqrt{5^2} \times \sqrt{x^2} \rightarrow 5x\sqrt{2} \).
- Simplifying: Multiply the factors outside the square root and leave the remaining factors inside.
- Example: \( 5x\sqrt{2} \) is the simplified form of \( \sqrt{50x^2} \).
Understanding and applying these properties and steps will allow you to simplify square roots containing variables effectively. This skill is crucial for solving complex algebraic expressions and advancing in your mathematical studies.
Basic Properties of Square Roots
Square roots are a critical concept in algebra, representing a value that, when multiplied by itself, yields the original number. Understanding the basic properties of square roots is essential for simplifying expressions that include them, especially when variables are involved. Here are the key properties:
Properties of Square Roots
- Non-Negative: The square root of a non-negative number is also non-negative. For any \(a \geq 0\), \( \sqrt{a} \geq 0 \).
- Product Property: The square root of a product is the product of the square roots. \[ \sqrt{ab} = \sqrt{a} \times \sqrt{b} \] This property is useful when breaking down complex expressions into simpler factors.
- Quotient Property: The square root of a quotient is the quotient of the square roots. \[ \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \] This property is particularly helpful when simplifying fractions within square roots.
- Power Property: The square root of a squared number is the absolute value of the original number. \[ \sqrt{a^2} = |a| \] This ensures that the result is non-negative.
- Zero Property: The square root of zero is zero. \[ \sqrt{0} = 0 \] This is straightforward but important to remember.
Examples of Applying Square Root Properties
Let's apply these properties to simplify some expressions:
- Simplify \( \sqrt{36} \):
- Using the power property: \( \sqrt{36} = \sqrt{6^2} = |6| = 6 \).
- Simplify \( \sqrt{50} \):
- Factorize the number: \( 50 = 2 \times 5^2 \).
- Apply the product property: \( \sqrt{50} = \sqrt{2 \times 5^2} = \sqrt{2} \times \sqrt{5^2} = 5\sqrt{2} \).
- Simplify \( \sqrt{\frac{9}{16}} \):
- Apply the quotient property: \( \sqrt{\frac{9}{16}} = \frac{\sqrt{9}}{\sqrt{16}} = \frac{3}{4} \).
By mastering these properties, you will be well-equipped to handle more complex algebraic expressions involving square roots, whether they include variables or not. Practicing these properties will enhance your mathematical skills and provide a strong foundation for advanced topics.
Factorizing Numbers and Variables
Factorizing numbers and variables is a crucial step in simplifying square root expressions. This process involves breaking down a number or variable into its prime factors or basic components, making it easier to simplify the expression inside the square root. Here’s a detailed, step-by-step guide to factorizing numbers and variables:
Step-by-Step Guide to Factorizing
- Identify the Number or Variable:
Determine the number or variable that needs to be factorized.
- Example: Factorize \( 72y^4 \).
- Prime Factorization of Numbers:
Break down the number into its prime factors.
- Example: \( 72 = 2^3 \times 3^2 \).
- Factorizing Variables:
Express the variable in its simplest exponential form.
- Example: \( y^4 = y \times y \times y \times y = (y^2)^2 \).
- Combine Factors:
Combine the prime factors of the number and the factorized form of the variable.
- Example: \( 72y^4 = 2^3 \times 3^2 \times (y^2)^2 \).
Examples of Factorizing
- Example 1: Factorize \( 50x^2 \)
- Identify the number and variable: \( 50 \) and \( x^2 \).
- Prime factorize the number: \( 50 = 2 \times 5^2 \).
- Factorize the variable: \( x^2 = x \times x \).
- Combine factors: \( 50x^2 = 2 \times 5^2 \times x^2 \).
- Example 2: Factorize \( 32a^3 \)
- Identify the number and variable: \( 32 \) and \( a^3 \).
- Prime factorize the number: \( 32 = 2^5 \).
- Factorize the variable: \( a^3 = a \times a \times a \).
- Combine factors: \( 32a^3 = 2^5 \times a^3 \).
Practice Problems
Try factorizing the following expressions:
- Factorize \( 45b^5 \)
- Factorize \( 98c^2 \)
- Factorize \( 54d^6 \)
By mastering the art of factorizing numbers and variables, you will find it much easier to simplify square root expressions, enhancing your overall algebra skills.

Identifying and Grouping Pairs
After factorizing the numbers and variables inside a square root, the next critical step is identifying and grouping pairs of factors. This process simplifies the square root by allowing certain factors to move outside the radical. Here’s a detailed guide on how to identify and group pairs:
Step-by-Step Guide to Identifying and Grouping Pairs
- Factorize the Expression:
Ensure that the number and variables are fully factorized into their prime factors or simplest exponential forms.
- Example: \( \sqrt{72y^4} \) is factorized as \( \sqrt{2^3 \times 3^2 \times y^4} \).
- Identify Pairs of Factors:
Look for pairs of identical factors in the factorized expression.
- Example: In \( \sqrt{2^3 \times 3^2 \times y^4} \), the pairs are \( 2^2 \), \( 3^2 \), and \( y^4 = (y^2)^2 \).
- Group the Pairs:
Group the identified pairs together. Each pair can be simplified as a single factor outside the square root.
- Example: Group \( 2^2 \) and \( 3^2 \) as \( (2^2) \) and \( (3^2) \).
- Simplify the Expression:
Move one factor from each pair outside the square root, while the remaining factors stay inside.
- Example: \( \sqrt{2^3 \times 3^2 \times y^4} = \sqrt{2^2 \times 2 \times 3^2 \times y^4} = 6y^2\sqrt{2} \).
Examples of Identifying and Grouping Pairs
- Example 1: Simplify \( \sqrt{50x^2} \)
- Factorize: \( 50 = 2 \times 5^2 \) and \( x^2 \).
- Identify pairs: \( 5^2 \) and \( x^2 \).
- Group pairs: \( (5^2) \) and \( (x^2) \).
- Move outside: \( 5x\sqrt{2} \).
- Example 2: Simplify \( \sqrt{18b^5} \)
- Factorize: \( 18 = 2 \times 3^2 \) and \( b^5 = b^4 \times b = (b^2)^2 \times b \).
- Identify pairs: \( 3^2 \) and \( (b^2)^2 \).
- Group pairs: \( (3^2) \) and \( (b^2)^2 \).
- Move outside: \( 3b^2\sqrt{2b} \).
Practice Problems
Try identifying and grouping pairs in the following expressions:
- Simplify \( \sqrt{45c^6} \)
- Simplify \( \sqrt{98d^8} \)
- Simplify \( \sqrt{54e^3} \)
By practicing these steps and examples, you will gain proficiency in identifying and grouping pairs, which is crucial for simplifying square root expressions involving variables.
Moving Factors Outside the Square Root
Once you have identified and grouped pairs of factors inside the square root, the next step is to move these factors outside the square root. This process helps in simplifying the expression significantly. Here is a detailed, step-by-step guide to moving factors outside the square root:
Step-by-Step Guide to Moving Factors Outside
- Identify Pairs of Factors:
Ensure you have grouped pairs of identical factors from the factorized form.
- Example: In \( \sqrt{72y^4} \), the pairs are \( 2^2 \), \( 3^2 \), and \( (y^2)^2 \).
- Move Each Pair Outside:
For each pair identified, move one of the factors outside the square root. This step utilizes the property \( \sqrt{a^2} = a \).
- Example:
- Start with \( \sqrt{72y^4} = \sqrt{2^3 \times 3^2 \times y^4} \).
- Identify and group pairs: \( \sqrt{(2^2 \times 2) \times 3^2 \times (y^2)^2} \).
- Move pairs outside: \( 6y^2\sqrt{2} \).
- Example:
- Simplify Remaining Expression:
Ensure the expression outside the square root is in its simplest form and that any remaining factors inside the square root are also simplified.
- Example: \( 6y^2\sqrt{2} \) is the simplified form where 6 and \( y^2 \) are outside and \( 2 \) remains inside the square root.
Examples of Moving Factors Outside
- Example 1: Simplify \( \sqrt{50x^2} \)
- Factorize: \( 50 = 2 \times 5^2 \) and \( x^2 \).
- Identify pairs: \( 5^2 \) and \( x^2 \).
- Move pairs outside: \( 5x \).
- Simplify: \( 5x\sqrt{2} \).
- Example 2: Simplify \( \sqrt{18b^5} \)
- Factorize: \( 18 = 2 \times 3^2 \) and \( b^5 = b^4 \times b = (b^2)^2 \times b \).
- Identify pairs: \( 3^2 \) and \( (b^2)^2 \).
- Move pairs outside: \( 3b^2 \).
- Simplify: \( 3b^2\sqrt{2b} \).
Practice Problems
Try simplifying the following expressions by moving factors outside the square root:
- Simplify \( \sqrt{45c^6} \)
- Simplify \( \sqrt{98d^8} \)
- Simplify \( \sqrt{54e^3} \)
By mastering these steps and practicing with different examples, you will be able to simplify complex square root expressions involving variables, making them much easier to work with in algebraic problems.
Multiplying Inside and Outside the Square Root
In some cases, simplifying square root expressions with variables involves multiplying factors both inside and outside the square root. Understanding how to properly handle these multiplications can further simplify the expression. Here’s a detailed, step-by-step guide to multiplying inside and outside the square root:
Step-by-Step Guide to Multiplying Inside and Outside the Square Root
- Understand the Properties:
Recall the basic properties of square roots and multiplication:
- \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\)
- \(\sqrt{a^2} = a\)
- Multiply Inside the Square Root:
When multiplying two square roots, you can combine the radicands (the numbers inside the square roots):
- Example: \( \sqrt{3} \times \sqrt{12} = \sqrt{3 \times 12} = \sqrt{36} = 6 \).
- Multiply Factors Outside the Square Root:
If you have factors outside the square root, multiply them directly:
- Example: \( 2 \times \sqrt{3} \times 4 \times \sqrt{5} = (2 \times 4) \times \sqrt{3 \times 5} = 8 \times \sqrt{15} \).
- Combine Inside and Outside Factors:
When you have both inside and outside factors, treat them separately before combining:
- Example: \( 3 \sqrt{2} \times 4 \sqrt{5} = (3 \times 4) \times \sqrt{2 \times 5} = 12 \sqrt{10} \).
Examples of Multiplying Inside and Outside the Square Root
- Example 1: Simplify \( 2 \sqrt{3} \times 5 \sqrt{7} \)
- Multiply outside factors: \( 2 \times 5 = 10 \).
- Multiply inside the square root: \( \sqrt{3} \times \sqrt{7} = \sqrt{21} \).
- Combine: \( 10 \sqrt{21} \).
- Example 2: Simplify \( 6 \sqrt{2x} \times 3 \sqrt{5y} \)
- Multiply outside factors: \( 6 \times 3 = 18 \).
- Multiply inside the square root: \( \sqrt{2x} \times \sqrt{5y} = \sqrt{10xy} \).
- Combine: \( 18 \sqrt{10xy} \).
Practice Problems
Try multiplying the following square root expressions:
- Simplify \( 4 \sqrt{3a} \times 2 \sqrt{6b} \)
- Simplify \( 5 \sqrt{7x} \times 3 \sqrt{2y} \)
- Simplify \( 7 \sqrt{5m} \times 4 \sqrt{3n} \)
By mastering these steps and practicing with different expressions, you will be able to efficiently multiply factors both inside and outside the square root, greatly simplifying your algebraic work.
Common Mistakes to Avoid
Simplifying square roots with variables can sometimes be tricky, and there are several common mistakes that students often make. Understanding these mistakes and how to avoid them will help you simplify expressions correctly and efficiently.
Mistake 1: Incorrectly Factorizing the Radicand
When breaking down the radicand into its prime factors, ensure that you correctly identify all the factors. Missing a factor or incorrectly factoring the expression can lead to incorrect simplification.
- Example: Incorrectly factorizing \( \sqrt{50} \) as \( 5 \sqrt{2} \) instead of \( 5 \sqrt{2} \).
Mistake 2: Failing to Identify All Pairs
Always look for pairs of factors inside the square root. Missing pairs means you won’t simplify the expression fully.
- Example: Simplifying \( \sqrt{18} \) as \( \sqrt{9 \times 2} = 3 \sqrt{2} \) instead of leaving it as \( \sqrt{18} \).
Mistake 3: Not Simplifying Variables Correctly
Variables under the square root need to be simplified in the same way as numerical factors. Look for pairs of variables as well.
- Example: Simplifying \( \sqrt{x^4} \) as \( \sqrt{x^2 \cdot x^2} = x^2 \), not \( x \sqrt{x^2} \).
Mistake 4: Incorrectly Combining Factors
When moving factors outside the square root, ensure that you correctly multiply them. Also, remember to multiply any coefficients that were already outside the square root.
- Example: Simplifying \( 2 \sqrt{3} \times 3 \sqrt{5} = (2 \times 3) \times \sqrt{3 \times 5} = 6 \sqrt{15} \).
Mistake 5: Ignoring the Absolute Value
When simplifying square roots that involve variables raised to an even power, remember to consider the absolute value. This is especially important in more advanced algebra.
- Example: Simplifying \( \sqrt{x^2} \) as \( |x| \), not just \( x \).
Mistake 6: Misinterpreting the Square Root Property
The property \( \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \) only holds if \( a \) and \( b \) are non-negative. Be cautious about applying this property when negative values are involved.
- Example: Applying \( \sqrt{-4 \cdot 4} = \sqrt{-4} \cdot \sqrt{4} \), which is not valid because it involves the square root of a negative number.
Tips to Avoid Mistakes
Here are some tips to help you avoid these common mistakes:
- Double-check your factorization of the radicand.
- Carefully identify all pairs of factors and variables.
- Verify each step of your simplification process.
- Consider the absolute value when dealing with variables.
- Be cautious with properties involving negative values.
By being aware of these common mistakes and following these tips, you can improve your skills in simplifying square roots with variables and avoid common pitfalls.

Advanced Techniques for Complex Expressions
In this section, we will delve into advanced techniques for simplifying square roots that contain variables and more complex expressions. These techniques will help you handle expressions that go beyond the basics, making it easier to work with them in algebra and other areas of mathematics.
1. Simplifying Expressions with Multiple Variables
When dealing with square roots that involve multiple variables, the key is to simplify each part of the expression separately before combining them. Here are the steps:
- Identify and separate the numerical and variable parts of the expression.
- Simplify the numerical part by factoring and finding perfect squares.
- Simplify the variable part by grouping variables into pairs.
- Combine the simplified numerical and variable parts.
Example:
\[
\sqrt{50x^4y^3} = \sqrt{50} \cdot \sqrt{x^4} \cdot \sqrt{y^3}
\]
Factor each part:
- \(\sqrt{50} = \sqrt{25 \cdot 2} = 5\sqrt{2}\)
- \(\sqrt{x^4} = x^2\)
- \(\sqrt{y^3} = \sqrt{y^2 \cdot y} = y\sqrt{y}\)
Combine the results:
\[
5x^2y\sqrt{2y}
\]
2. Simplifying Nested Square Roots
Nested square roots can be simplified by rationalizing them, which involves removing the square root from the denominator. Here is a step-by-step process:
- Identify the nested square root.
- Multiply the numerator and the denominator by the conjugate of the denominator.
- Simplify the resulting expression.
Example:
\[
\frac{1}{\sqrt{3} + \sqrt{2}}
\]
Multiply by the conjugate:
\[
\frac{1}{\sqrt{3} + \sqrt{2}} \cdot \frac{\sqrt{3} - \sqrt{2}}{\sqrt{3} - \sqrt{2}} = \frac{\sqrt{3} - \sqrt{2}}{(\sqrt{3})^2 - (\sqrt{2})^2} = \frac{\sqrt{3} - \sqrt{2}}{3 - 2} = \sqrt{3} - \sqrt{2}
\]
3. Simplifying Expressions with Fractional Exponents
Expressions with fractional exponents can also be simplified using the properties of exponents and radicals:
- Rewrite the expression with fractional exponents as radicals.
- Simplify the radicals as usual.
Example:
\[
(x^2y)^{3/2} = \sqrt{(x^2y)^3} = \sqrt{x^6y^3} = x^3y^{3/2} = x^3\sqrt{y^3} = x^3y\sqrt{y}
\]
4. Using the Binomial Theorem for Complex Expressions
The Binomial Theorem can be useful for expanding and simplifying expressions involving square roots:
Example:
\[
(\sqrt{a} + \sqrt{b})^2 = a + 2\sqrt{ab} + b
\]
5. Solving Equations with Square Roots
Sometimes, simplifying square roots is part of solving equations. Here’s an example:
Example:
Solve \(\sqrt{2x + 3} = x - 1\)
- Square both sides to eliminate the square root:
- Expand and simplify:
- Rearrange into a standard quadratic equation:
- Solve the quadratic equation using the quadratic formula:
\[
2x + 3 = (x - 1)^2
\]
\[
2x + 3 = x^2 - 2x + 1
\]
\[
x^2 - 4x - 2 = 0
\]
\[
x = \frac{4 \pm \sqrt{16 + 8}}{2} = \frac{4 \pm \sqrt{24}}{2} = \frac{4 \pm 2\sqrt{6}}{2} = 2 \pm \sqrt{6}
\]
By mastering these advanced techniques, you'll be able to tackle even the most complex expressions involving square roots and variables with confidence.
Practice Problems and Solutions
Practice simplifying square roots that contain variables to reinforce your understanding and mastery of the concepts. Below are a series of problems followed by detailed solutions to guide you through the process.
Problem 1
Simplify: \( \sqrt{50x^4} \)
Solution:
- Factorize the number and variables inside the square root: \( \sqrt{50x^4} = \sqrt{25 \cdot 2 \cdot x^4} \).
- Separate the factors into individual square roots: \( \sqrt{25} \cdot \sqrt{2} \cdot \sqrt{x^4} \).
- Simplify each square root: \( 5 \cdot \sqrt{2} \cdot x^2 \).
The simplified form is: \( 5x^2 \sqrt{2} \).
Problem 2
Simplify: \( \sqrt{72y^6} \)
Solution:
- Factorize the number and variables inside the square root: \( \sqrt{72y^6} = \sqrt{36 \cdot 2 \cdot y^6} \).
- Separate the factors into individual square roots: \( \sqrt{36} \cdot \sqrt{2} \cdot \sqrt{y^6} \).
- Simplify each square root: \( 6 \cdot \sqrt{2} \cdot y^3 \).
The simplified form is: \( 6y^3 \sqrt{2} \).
Problem 3
Simplify: \( \sqrt{125x^3y^4} \)
Solution:
- Factorize the number and variables inside the square root: \( \sqrt{125x^3y^4} = \sqrt{25 \cdot 5 \cdot x^2 \cdot x \cdot y^4} \).
- Separate the factors into individual square roots: \( \sqrt{25} \cdot \sqrt{5} \cdot \sqrt{x^2} \cdot \sqrt{x} \cdot \sqrt{y^4} \).
- Simplify each square root: \( 5 \cdot \sqrt{5} \cdot x \cdot \sqrt{x} \cdot y^2 \).
The simplified form is: \( 5xy^2 \sqrt{5x} \).
Problem 4
Simplify: \( \sqrt{48x^2y^5} \)
Solution:
- Factorize the number and variables inside the square root: \( \sqrt{48x^2y^5} = \sqrt{16 \cdot 3 \cdot x^2 \cdot y^4 \cdot y} \).
- Separate the factors into individual square roots: \( \sqrt{16} \cdot \sqrt{3} \cdot \sqrt{x^2} \cdot \sqrt{y^4} \cdot \sqrt{y} \).
- Simplify each square root: \( 4 \cdot \sqrt{3} \cdot x \cdot y^2 \cdot \sqrt{y} \).
The simplified form is: \( 4xy^2 \sqrt{3y} \).
Problem 5
Simplify: \( \sqrt{98x^7y^2} \)
Solution:
- Factorize the number and variables inside the square root: \( \sqrt{98x^7y^2} = \sqrt{49 \cdot 2 \cdot x^6 \cdot x \cdot y^2} \).
- Separate the factors into individual square roots: \( \sqrt{49} \cdot \sqrt{2} \cdot \sqrt{x^6} \cdot \sqrt{x} \cdot \sqrt{y^2} \).
- Simplify each square root: \( 7 \cdot \sqrt{2} \cdot x^3 \cdot \sqrt{x} \cdot y \).
The simplified form is: \( 7x^3y \sqrt{2x} \).
Problem 6
Simplify: \( \sqrt{200x^5y^8} \)
Solution:
- Factorize the number and variables inside the square root: \( \sqrt{200x^5y^8} = \sqrt{100 \cdot 2 \cdot x^4 \cdot x \cdot y^8} \).
- Separate the factors into individual square roots: \( \sqrt{100} \cdot \sqrt{2} \cdot \sqrt{x^4} \cdot \sqrt{x} \cdot \sqrt{y^8} \).
- Simplify each square root: \( 10 \cdot \sqrt{2} \cdot x^2 \cdot \sqrt{x} \cdot y^4 \).
The simplified form is: \( 10x^2y^4 \sqrt{2x} \).
Continue practicing with these problems and refer back to the solutions to ensure your understanding and accuracy in simplifying square roots with variables.
Applications in Algebra and Beyond
Simplifying square roots with variables is not just an isolated algebraic skill; it has practical applications across various areas of mathematics and science. Here are some key applications:
1. Solving Quadratic Equations
In many quadratic equations, the solutions involve square roots. Understanding how to simplify these roots when they include variables is crucial.
For example, solving \( ax^2 + bx + c = 0 \) using the quadratic formula:
\[
x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
\]
If the discriminant (\( b^2 - 4ac \)) contains variables, simplifying the square root is essential to find the correct solutions.
2. Geometry and Trigonometry
In geometry, simplifying square roots of variables is used in problems involving the Pythagorean theorem and distance formulas. For example, the distance between two points \((x_1, y_1)\) and \((x_2, y_2)\) in the coordinate plane is given by:
\[
d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\]
If \(x_1\), \(x_2\), \(y_1\), and \(y_2\) are expressions containing variables, you will need to simplify the resulting square root.
3. Physics and Engineering
In physics, square roots appear in formulas for wave speeds, energy calculations, and other applications. For instance, the formula for the period \( T \) of a pendulum is:
\[
T = 2\pi \sqrt{\frac{L}{g}}
\]
where \( L \) is the length of the pendulum and \( g \) is the acceleration due to gravity. If \( L \) is expressed as a variable equation, simplifying the square root is necessary to understand the period's dependency on different factors.
4. Statistics
The standard deviation formula in statistics includes a square root:
\[
\sigma = \sqrt{\frac{\sum (x_i - \mu)^2}{N}}
\]
Where \( x_i \) represents each value, \( \mu \) is the mean, and \( N \) is the number of values. Simplifying this root is crucial in data analysis, especially when dealing with variable expressions.
5. Complex Numbers
In advanced algebra, dealing with complex numbers often involves simplifying square roots of negative numbers. For example, the square root of a negative variable \( -x \) can be simplified using imaginary units:
\[
\sqrt{-x} = i\sqrt{x}
\]
This concept is fundamental in solving equations involving complex numbers.
6. Computer Science
Algorithms in computer science, particularly those involving graphics and geometry, frequently require the simplification of square roots with variables. Understanding how to handle these calculations is essential for optimizing code and ensuring accurate results.
By mastering the simplification of square roots with variables, you enhance your problem-solving toolkit, enabling you to tackle a wide range of mathematical, scientific, and engineering challenges.
Useful Formulas and Tips
Simplifying square roots that include variables can be made easier with a few key formulas and tips. Here are some useful guidelines:
- Basic Formula for Square Roots: \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\). This can be applied to both numbers and variables.
- Simplifying Variables: For any variable raised to an even power, \( \sqrt{x^{2n}} = x^n \). For example, \( \sqrt{x^4} = x^2 \).
- Combining Factors: If you have a product under a square root, factor each part separately and then combine. For example, \( \sqrt{50x^4} = \sqrt{25 \cdot 2 \cdot x^4} = 5x^2\sqrt{2} \).
Here are some additional formulas and tips:
Useful Formulas
- \(\sqrt{x^2} = |x|\)
- \(\sqrt{a^2b^2} = ab\)
- \(\sqrt{a^m \cdot b^n} = a^{m/2} \cdot b^{n/2}\)
Tips for Simplifying Square Roots
- Identify and separate the numerical and variable parts of the radicand (the expression under the square root).
- Factorize the number into its prime factors and the variables into their lowest possible powers.
- Group the factors into pairs for the variables, and apply the square root to each pair.
- Move one factor from each pair outside the square root, leaving any unpaired factors inside.
Let's look at some examples to illustrate these steps:
Example 1
Simplify \( \sqrt{72x^5} \)
- Factorize: \( 72 = 2^3 \cdot 3^2 \), so \( 72x^5 = 2^3 \cdot 3^2 \cdot x^5 \).
- Group pairs: \( \sqrt{2^3 \cdot 3^2 \cdot x^5} = \sqrt{(2^2 \cdot 2) \cdot (3^2) \cdot (x^4 \cdot x)} \).
- Apply square root: \( = 3x^2 \sqrt{2x} \).
Example 2
Simplify \( \sqrt{50y^6} \)
- Factorize: \( 50 = 2 \cdot 5^2 \), so \( 50y^6 = 2 \cdot 5^2 \cdot y^6 \).
- Group pairs: \( \sqrt{2 \cdot 5^2 \cdot y^6} = \sqrt{(5^2) \cdot (y^6) \cdot 2} \).
- Apply square root: \( = 5y^3 \sqrt{2} \).
With these formulas and tips, simplifying square roots with variables becomes a systematic process that can be applied to various algebraic expressions.
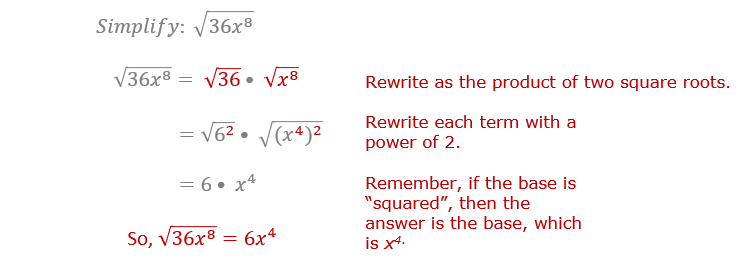
Conclusion
Simplifying square roots with variables is an essential skill in algebra that extends to various mathematical applications. By mastering the fundamental properties and techniques, such as identifying perfect squares, using the product and quotient properties, and handling variables with both even and odd exponents, students can confidently approach more complex expressions.
Throughout this guide, we explored the basic properties of square roots, step-by-step procedures for simplification, and practical examples to illustrate these concepts. We also delved into advanced techniques and provided useful formulas and tips to enhance your understanding.
To recap, here are the key takeaways:
- Factorize the expression under the square root to identify perfect squares.
- Use the product property: \( \sqrt{xy} = \sqrt{x} \cdot \sqrt{y} \).
- Use the quotient property: \( \sqrt{\frac{x}{y}} = \frac{\sqrt{x}}{\sqrt{y}} \).
- For variables with even exponents, divide the exponent by 2.
- For variables with odd exponents, separate the variable into factors with one even and one exponent of 1, then simplify.
By practicing these methods, you can simplify square root expressions with variables more effectively, making complex algebraic problems more manageable. Remember, consistent practice is key to mastering these skills. We hope this guide has provided you with the necessary tools and confidence to tackle square root simplifications in your mathematical journey.
Keep exploring and applying these techniques in different contexts, and you'll find them invaluable in solving a wide range of algebraic problems and beyond.
Video hướng dẫn cách đơn giản hóa căn bậc hai với biến số một cách chi tiết và dễ hiểu. Phù hợp cho học sinh và người yêu thích toán học.
Căn Bậc Hai với Biến Số (Đơn Giản Hóa Toán Học)
READ MORE:
Video hướng dẫn cách đơn giản hóa căn bậc hai với biến số, số mũ, phân số và căn bậc ba. Phù hợp cho học sinh học đại số và người yêu thích toán học.
Đơn Giản Hóa Căn Bậc Hai Với Biến Số, Số Mũ, Phân Số, Căn Bậc Ba - Đại Số











