Topic simplify square root of 56: Unlock the secrets of simplifying the square root of 56 with our comprehensive, easy-to-follow guide. Whether you're a student or a math enthusiast, this article breaks down the process into simple steps, helping you understand and master the concept. Dive in to simplify square roots with confidence and clarity!
Table of Content
- Simplifying the Square Root of 56
- Introduction to Simplifying Square Roots
- Understanding Prime Factorization
- Step-by-Step Guide to Simplifying the Square Root of 56
- Identifying Perfect Squares
- Extracting Factors from the Radical
- Combining Like Terms
- Final Simplified Form of Square Root of 56
- Common Mistakes to Avoid
- Additional Examples of Simplifying Square Roots
- Practice Problems
- References and Further Reading
- YOUTUBE: Hướng dẫn đơn giản hóa căn bậc hai của 56 bằng tiếng Việt. Video giải thích chi tiết từng bước và phù hợp cho bài viết về chủ đề này.
Simplifying the Square Root of 56
To simplify the square root of 56, we need to find the prime factorization of 56 and then simplify the radical by extracting squares.
Step-by-Step Process
-
First, find the prime factorization of 56.
\[
56 = 2 \times 28 = 2 \times 2 \times 14 = 2 \times 2 \times 2 \times 7 = 2^3 \times 7
\] -
Next, rewrite the square root of 56 using its prime factors.
\[
\sqrt{56} = \sqrt{2^3 \times 7}
\] -
Group the factors inside the square root in pairs of two.
\[
\sqrt{2^3 \times 7} = \sqrt{(2^2) \times 2 \times 7}
\] -
Extract the square root of the perfect square (which is 22) and move it outside the radical.
\[
\sqrt{(2^2) \times 2 \times 7} = 2 \sqrt{2 \times 7} = 2 \sqrt{14}
\]
Conclusion
Therefore, the simplified form of the square root of 56 is:
\[
\sqrt{56} = 2 \sqrt{14}
\]

READ MORE:
Introduction to Simplifying Square Roots
The process of simplifying square roots is a fundamental concept in algebra and is essential for solving various mathematical problems. Simplifying square roots involves reducing the expression to its simplest form, making it easier to work with in equations and other calculations. This section will guide you through the basics of simplifying square roots using the square root of 56 as an example.
To simplify a square root, you need to follow these general steps:
- Identify the prime factors of the number under the square root.
- Group the prime factors into pairs.
- Extract the pairs from under the radical sign, leaving any unpaired factors inside.
Let's apply these steps to simplify the square root of 56:
- Identify the prime factors:
The prime factorization of 56 is \( 2 \times 2 \times 2 \times 7 \) or \( 2^3 \times 7 \). - Group the factors:
Group the factors into pairs: \( (2 \times 2) \times (2 \times 7) \). We can see that \( 2^2 \) forms a pair. - Extract the pairs:
Take the square root of each pair and move it outside the radical sign. The pair \( 2^2 \) comes out as 2, and the remaining factors \( 2 \times 7 = 14 \) stay inside the radical.
Therefore, \( \sqrt{56} = \sqrt{2^2 \times 14} = 2\sqrt{14} \).
Thus, the simplified form of \( \sqrt{56} \) is \( 2\sqrt{14} \).
Understanding this process helps in simplifying other square roots and solving related mathematical problems more efficiently.
Understanding Prime Factorization
Prime factorization is a method of breaking down a composite number into its prime factors. A prime number is a number greater than 1 that has no positive divisors other than 1 and itself. Prime factorization helps in simplifying square roots by identifying the prime components of the number under the radical.
To understand prime factorization, let's break down the steps involved:
- Identify Prime Numbers: The first step is to know which numbers are prime. For example, 2, 3, 5, 7, 11, 13, etc., are prime numbers.
- Divide by Smallest Prime: Start by dividing the number by the smallest prime number (2) and continue dividing by prime numbers until the quotient is 1.
- List Prime Factors: Write down all the prime numbers you used as divisors. These are the prime factors of the original number.
Let's apply these steps to factorize 56:
- 56 is an even number, so we start by dividing it by 2:
- 56 ÷ 2 = 28
- 28 is also even, so we divide by 2 again:
- 28 ÷ 2 = 14
- 14 is even, so we divide by 2 one more time:
- 14 ÷ 2 = 7
- 7 is a prime number and cannot be divided further.
Therefore, the prime factorization of 56 is:
\[56 = 2 \times 2 \times 2 \times 7 = 2^3 \times 7\]
Prime factorization is crucial in simplifying square roots. For instance, simplifying the square root of 56 involves using these prime factors:
\[\sqrt{56} = \sqrt{2^3 \times 7} = \sqrt{2^2 \times 2 \times 7} = \sqrt{2^2} \times \sqrt{2 \times 7} = 2 \sqrt{14}\]
By understanding and applying prime factorization, simplifying square roots becomes a straightforward process, making it easier to work with radical expressions.
Step-by-Step Guide to Simplifying the Square Root of 56
In this section, we will provide a detailed, step-by-step guide to simplify the square root of 56.
-
Identify Factors:
First, we need to identify the factors of 56. The goal is to find the largest perfect square factor.
- Factors of 56: 1, 2, 4, 7, 8, 14, 28, 56
- Perfect square factors: 1, 4
- Largest perfect square factor: 4
-
Apply the Product Rule for Radicals:
We use the product rule for radicals which states: \(\sqrt{ab} = \sqrt{a} \cdot \sqrt{b}\).
For 56, we have:
\[
\sqrt{56} = \sqrt{4 \cdot 14}
\] -
Separate the Radicals:
Next, we separate the square root into two parts:
\[
\sqrt{56} = \sqrt{4} \cdot \sqrt{14}
\] -
Simplify the Perfect Square:
Since 4 is a perfect square, we can simplify \(\sqrt{4}\) to 2:
\[
\sqrt{4} \cdot \sqrt{14} = 2\sqrt{14}
\] -
Write the Final Simplified Form:
The simplified form of the square root of 56 is:
\[
\sqrt{56} = 2\sqrt{14}
\]
By following these steps, we have simplified \(\sqrt{56}\) to \(2\sqrt{14}\).
Identifying Perfect Squares
When simplifying square roots, it is essential to identify perfect squares within the radicand (the number under the square root symbol). A perfect square is a number that can be expressed as the square of an integer.
For instance, the numbers 1, 4, 9, 16, 25, and 36 are all perfect squares because:
- 1 = 12
- 4 = 22
- 9 = 32
- 16 = 42
- 25 = 52
- 36 = 62
To simplify a square root, we look for the largest perfect square factor of the number inside the radical. Let's take the square root of 56 as an example:
First, identify the perfect squares that are factors of 56. The number 4 is a perfect square and a factor of 56 because 56 = 4 × 14.
Rewrite the square root of 56 using this factorization:
\(\sqrt{56} = \sqrt{4 \times 14}\)
Apply the property of square roots that allows you to separate the factors:
\(\sqrt{4 \times 14} = \sqrt{4} \times \sqrt{14}\)
Simplify the square root of the perfect square:
\(\sqrt{4} = 2\)
Combine the simplified square root with the remaining factor:
\(\sqrt{4} \times \sqrt{14} = 2\sqrt{14}\)
Therefore, the simplified form of \(\sqrt{56}\) is \(2\sqrt{14}\). Identifying and using perfect squares is a key step in simplifying square roots efficiently.
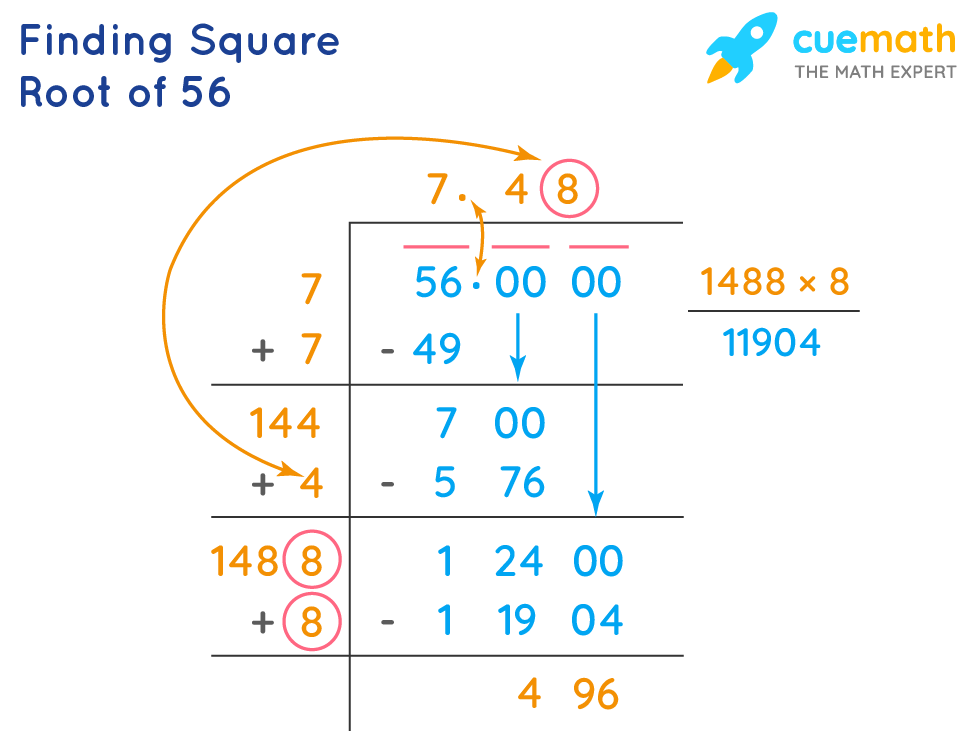
Extracting Factors from the Radical
When simplifying square roots, one useful technique is to extract factors from the radical. This process involves identifying the factors of the number under the radical sign and simplifying them to find the simplest form.
Let's use the square root of 56 as an example to illustrate this technique:
-
List the Factors of 56:
- 1, 2, 4, 7, 8, 14, 28, 56
-
Identify the Perfect Squares:
From the list of factors, identify the perfect squares. The perfect squares in the list of factors are 1 and 4.
-
Divide by the Largest Perfect Square:
Divide 56 by the largest perfect square found in the previous step:
\[ \frac{56}{4} = 14 \]
-
Calculate the Square Root of the Perfect Square:
The square root of 4 is 2:
\[ \sqrt{4} = 2 \]
-
Simplify the Expression:
Combine the results to express the original square root in its simplest form:
\[ \sqrt{56} = \sqrt{4 \times 14} = \sqrt{4} \times \sqrt{14} = 2 \sqrt{14} \]
By following these steps, you can extract factors from the radical and simplify square roots efficiently. This method is particularly useful when dealing with larger numbers or when you need to perform further calculations.
Combining Like Terms
Combining like terms is a fundamental process in simplifying mathematical expressions. When dealing with radicals, particularly square roots, it involves bringing together terms that have the same radicand. Here’s a detailed guide to combining like terms:
-
Identify Like Terms:
Like terms are those that contain the same variable raised to the same power. For square roots, this means they must have the same radicand. For example, \( \sqrt{2} \) and \( 3\sqrt{2} \) are like terms because they both have \( \sqrt{2} \).
-
Combine the Coefficients:
Once like terms are identified, add or subtract their coefficients while keeping the radical part unchanged. For example:
\( 2\sqrt{3} + 5\sqrt{3} = (2 + 5)\sqrt{3} = 7\sqrt{3} \)
Similarly:
\( 6\sqrt{7} - 2\sqrt{7} = (6 - 2)\sqrt{7} = 4\sqrt{7} \)
-
Example Problem:
Consider the expression \( 3\sqrt{14} + 2\sqrt{14} \):
Since both terms have the same radicand \( \sqrt{14} \), combine their coefficients:
\( 3\sqrt{14} + 2\sqrt{14} = (3 + 2)\sqrt{14} = 5\sqrt{14} \)
-
Check Your Work:
Always recheck to ensure that only like terms were combined and the radicand remains the same. Incorrectly combining unlike terms will lead to errors.
Combining like terms simplifies the expression and makes it easier to work with in further calculations. It is an essential skill in algebra and higher-level mathematics.
Final Simplified Form of Square Root of 56
To find the final simplified form of the square root of 56, follow these steps:
First, find the prime factorization of 56:
\[ 56 = 2^3 \times 7 \]Group the factors in pairs of two:
\[ 56 = (2^2) \times (2 \times 7) \]Take the square root of each pair of factors:
\[ \sqrt{56} = \sqrt{2^2} \times \sqrt{2 \times 7} \]Simplify the square roots:
\[ \sqrt{56} = 2 \sqrt{14} \]Therefore, the final simplified form of the square root of 56 is:
\[ \sqrt{56} = 2 \sqrt{14} \]
In decimal form, this is approximately:
\[ 2 \sqrt{14} \approx 7.483 \]
Common Mistakes to Avoid
When simplifying square roots, it's important to be mindful of common errors. Avoiding these mistakes can help ensure accurate and efficient solutions:
- Overlooking Perfect Squares: Always check for perfect squares within the number. For example, in √56, 4 is a perfect square factor (since 4 × 14 = 56), which can simplify the process.
- Incorrect Prime Factorization: Ensure accurate prime factorization. Misidentifying prime factors can lead to incorrect simplification.
- Incomplete Simplification: Don't stop simplifying too early. Make sure to fully simplify the expression. For instance, continuing the simplification of √56 as 2√14 rather than stopping at √56.
- Forgetting to Rationalize the Denominator: If the square root appears in a fraction's denominator, remember to rationalize it. For example, convert 1/√56 to √56/56.
- Rushing Through Calculations: Take your time to verify each step, ensuring no errors in the simplification process.
By being aware of these common mistakes, you can simplify square roots more effectively and accurately.

Additional Examples of Simplifying Square Roots
In this section, we will explore several examples of how to simplify square roots. These examples will help solidify the concepts and techniques discussed earlier.
Example 1: Simplifying \(\sqrt{72}\)
To simplify \(\sqrt{72}\), we need to find the prime factorization of 72:
- 72 can be expressed as \(72 = 2^3 \times 3^2\).
- Next, group the prime factors in pairs: \(2^2 \times 2 \times 3^2\).
- Take one factor out of each pair: \(\sqrt{72} = \sqrt{(2^2) \times (3^2) \times 2}\).
- This simplifies to \(2 \times 3 \times \sqrt{2}\), which equals \(6\sqrt{2}\).
Example 2: Simplifying \(\sqrt{50}\)
Let's simplify \(\sqrt{50}\):
- Find the prime factors of 50: \(50 = 2 \times 5^2\).
- Group the factors: \(2 \times (5^2)\).
- Take one factor out of the pair: \(\sqrt{50} = \sqrt{2 \times 5^2}\).
- This simplifies to \(5\sqrt{2}\).
Example 3: Simplifying \(\sqrt{18}\)
To simplify \(\sqrt{18}\), follow these steps:
- Find the prime factorization of 18: \(18 = 2 \times 3^2\).
- Group the factors: \(2 \times (3^2)\).
- Take one factor out of the pair: \(\sqrt{18} = \sqrt{2 \times 3^2}\).
- This simplifies to \(3\sqrt{2}\).
Example 4: Simplifying \(\sqrt{200}\)
Now, let's simplify \(\sqrt{200}\):
- Prime factorize 200: \(200 = 2^3 \times 5^2\).
- Group the factors: \(2^2 \times 2 \times 5^2\).
- Take one factor out of each pair: \(\sqrt{200} = \sqrt{(2^2) \times (5^2) \times 2}\).
- This simplifies to \(2 \times 5 \times \sqrt{2}\), which equals \(10\sqrt{2}\).
Example 5: Simplifying \(\sqrt{45}\)
To simplify \(\sqrt{45}\), follow these steps:
- Prime factorize 45: \(45 = 3^2 \times 5\).
- Group the factors: \((3^2) \times 5\).
- Take one factor out of the pair: \(\sqrt{45} = \sqrt{3^2 \times 5}\).
- This simplifies to \(3\sqrt{5}\).
Conclusion
By practicing these examples, you will become more comfortable with the process of simplifying square roots. Remember to always look for perfect square factors and group them accordingly to simplify the expression effectively.
Practice Problems
Here are some practice problems to help you master the process of simplifying square roots, including the square root of 56.
-
Problem 1: Simplify the square root of 56.
- Find the prime factorization of 56.
- Write 56 as a product of its prime factors: \( 56 = 2^3 \times 7 \).
- Pair the factors: \( \sqrt{56} = \sqrt{2^2 \times 14} = 2\sqrt{14} \).
- The simplified form is \( 2\sqrt{14} \).
-
Problem 2: Simplify \( \sqrt{72} \).
- Find the prime factorization of 72.
- Write 72 as a product of its prime factors: \( 72 = 2^3 \times 3^2 \).
- Pair the factors: \( \sqrt{72} = \sqrt{2^2 \times 3^2 \times 2} = 6\sqrt{2} \).
- The simplified form is \( 6\sqrt{2} \).
-
Problem 3: Simplify \( \sqrt{98} \).
- Find the prime factorization of 98.
- Write 98 as a product of its prime factors: \( 98 = 2 \times 7^2 \).
- Pair the factors: \( \sqrt{98} = \sqrt{2 \times 7^2} = 7\sqrt{2} \).
- The simplified form is \( 7\sqrt{2} \).
-
Problem 4: Simplify \( \sqrt{50} \).
- Find the prime factorization of 50.
- Write 50 as a product of its prime factors: \( 50 = 2 \times 5^2 \).
- Pair the factors: \( \sqrt{50} = \sqrt{2 \times 5^2} = 5\sqrt{2} \).
- The simplified form is \( 5\sqrt{2} \).
-
Problem 5: Simplify \( \sqrt{200} \).
- Find the prime factorization of 200.
- Write 200 as a product of its prime factors: \( 200 = 2^3 \times 5^2 \).
- Pair the factors: \( \sqrt{200} = \sqrt{2^2 \times 2 \times 5^2} = 10\sqrt{2} \).
- The simplified form is \( 10\sqrt{2} \).
These practice problems should help reinforce the steps needed to simplify square roots effectively. For more practice, try simplifying other square roots and verify your answers with a calculator or algebraic methods.
References and Further Reading
For those looking to deepen their understanding of simplifying square roots and to explore additional resources, the following references and tools will be invaluable:
- - This online tool allows you to simplify a wide range of mathematical expressions, including square roots. It provides step-by-step solutions, making it an excellent resource for learning and verifying your work.
- - This specific example on Mathway shows the detailed steps to simplify the square root of 56, from factorizing the number to extracting the square root of perfect squares.
- - Number Maniacs provides a comprehensive breakdown of the steps involved in simplifying the square root of 56, making it easier to understand the process.
- - Khan Academy offers a video tutorial that explains the process of simplifying square roots, perfect for visual learners who benefit from seeing each step in action.
- - Symbolab's calculator helps you find and simplify square roots, providing step-by-step explanations to enhance your understanding of the methods used.
By exploring these resources, you can gain a deeper insight into the techniques and principles behind simplifying square roots, improving your mathematical skills and confidence.
Hướng dẫn đơn giản hóa căn bậc hai của 56 bằng tiếng Việt. Video giải thích chi tiết từng bước và phù hợp cho bài viết về chủ đề này.
Đơn Giản Hóa Căn Bậc Hai của 56: Sqrt(56)
READ MORE:
Hướng dẫn cách sử dụng phân tích thừa số nguyên tố để xác định căn bậc hai của số, cụ thể là sqrt(56). Video phù hợp cho bài viết về đơn giản hóa căn bậc hai của 56.
Cách sử dụng phân tích thừa số nguyên tố để xác định căn bậc hai của một số, sqrt(56)

















