Topic simplify square root of 150: Discover the simplest way to simplify the square root of 150 with our easy-to-follow guide. Learn the step-by-step process to break down √150 into its simplest form and understand the underlying concepts. Perfect for students, educators, and math enthusiasts looking to enhance their mathematical skills and knowledge.
Table of Content
- Simplifying the Square Root of 150
- Introduction to Square Roots
- Understanding the Basics of Square Roots
- Example: Simplifying the Square Root of 150
- Properties of Square Roots
- Square Roots of Non-Perfect Squares
- Prime Factorization Method
- Steps to Simplify Square Root of 150
- Example Problems
- Properties of Square Roots
- Applications of Simplified Square Roots
- Common Mistakes to Avoid
- YOUTUBE: Xem video hướng dẫn cách đơn giản hóa căn bậc hai của 150 để hiểu rõ hơn về quá trình tính toán và áp dụng trong các tình huống thực tế.
Simplifying the Square Root of 150
The square root of 150 can be simplified using prime factorization and properties of square roots. Below is a detailed explanation of how to simplify .
Steps to Simplify
- Find the prime factorization of 150:
- 150 = 2 × 3 × 5 × 5
- Group the prime factors into pairs:
- 150 = 2 × 3 × (5 × 5)
- Rewrite the square root of 150 using these factors:
- Extract the square root of the perfect square (25):
Conclusion
Thus, the simplified form of is .

READ MORE:
Introduction to Square Roots
The concept of square roots is fundamental in mathematics, particularly in algebra. A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 150 can be simplified by expressing 150 as the product of its prime factors. Let's explore this process step-by-step.
First, factorize 150:
- 150 = 2 × 3 × 5²
Next, use the property of square roots that allows us to separate the factors:
- \(\sqrt{150} = \sqrt{2 \times 3 \times 5^2}\)
Now, apply the square root to each factor:
- \(\sqrt{2 \times 3 \times 5^2} = \sqrt{2} \times \sqrt{3} \times \sqrt{5^2}\)
Simplify the expression by taking the square root of 5²:
- \(\sqrt{5^2} = 5\)
So, the simplified form of \(\sqrt{150}\) is:
- \(\sqrt{150} = 5\sqrt{6}\)
Understanding square roots and their simplification is essential for solving various mathematical problems. This knowledge is applicable in many areas, including geometry, physics, and engineering, where calculating precise values is crucial.
Understanding the Basics of Square Roots
The concept of square roots is fundamental in mathematics. A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 9 is 3 because 3 multiplied by 3 equals 9. The square root symbol is denoted as √, and it represents the principal or positive square root.
- The square root of a number n is written as √n.
- For instance, √25 = 5 because 52 = 25.
Example: Simplifying the Square Root of 150
To simplify the square root of 150, follow these steps:
- List the factors of 150: 1, 2, 3, 5, 6, 10, 15, 25, 30, 50, 75, 150.
- Identify the perfect squares among the factors: 1, 25.
- Divide 150 by the largest perfect square, which is 25: 150 ÷ 25 = 6.
- Take the square root of 25, which is 5.
- Combine the results to express √150: 5√6.
Therefore, the simplified form of √150 is 5√6.
Properties of Square Roots
Square roots have several important properties:
- Product Property: √a√b = √(a×b)
- Quotient Property: √(a/b) = √a/√b
These properties can be useful for simplifying more complex expressions involving square roots.
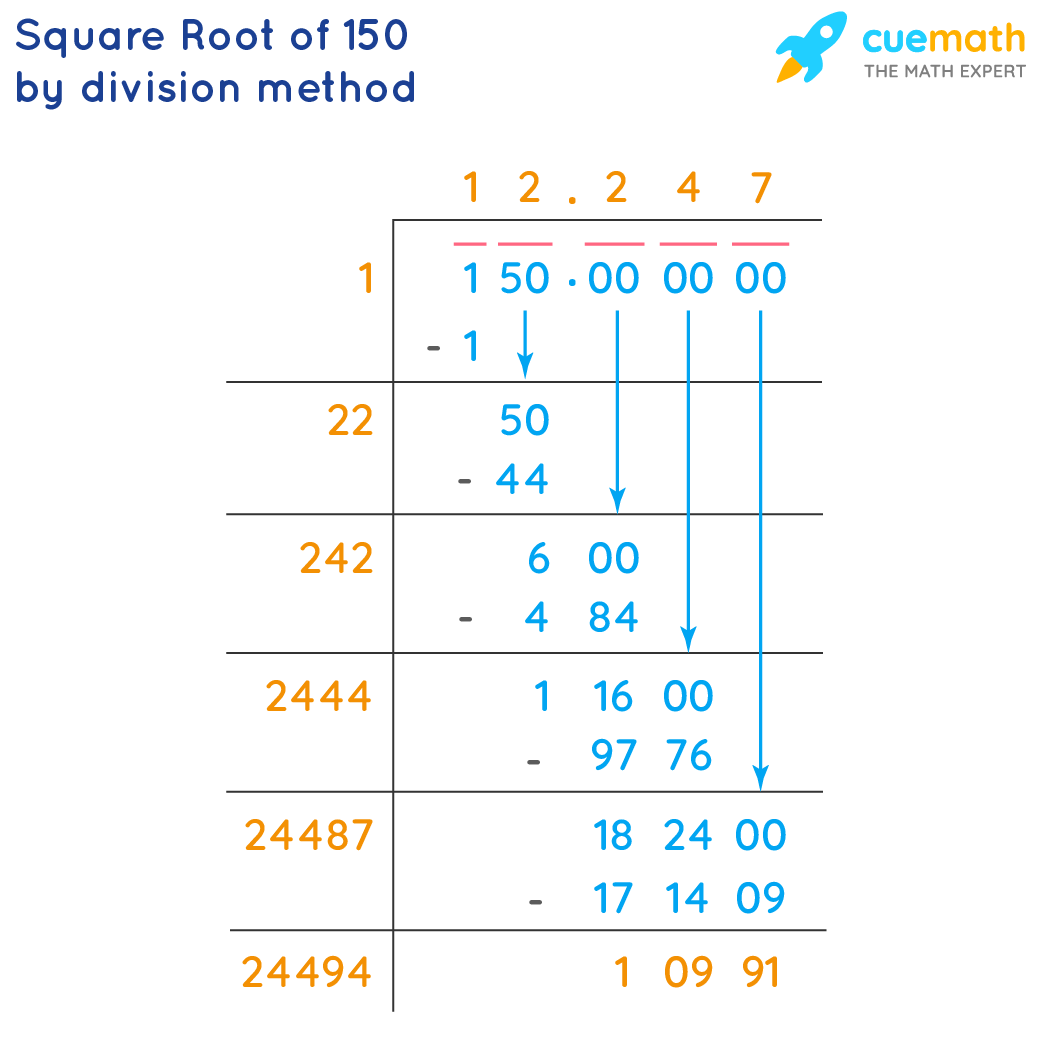
Square Roots of Non-Perfect Squares
For non-perfect squares, the square root will be an irrational number. For example, √150 is approximately 12.247, and it cannot be expressed as a simple fraction. Instead, it is usually left in its simplified radical form.
Understanding and simplifying square roots is a crucial skill in mathematics, useful in various applications ranging from algebra to geometry.
Prime Factorization Method
The prime factorization method is a systematic way to simplify the square root of a number by breaking it down into its prime factors. This method is particularly useful for simplifying square roots of non-perfect squares.
Let's apply the prime factorization method to simplify the square root of 150.
- Prime Factorization of 150:
First, we need to find the prime factors of 150. We can do this by dividing 150 by the smallest prime numbers:
- 150 is divisible by 2: 150 ÷ 2 = 75
- 75 is divisible by 3: 75 ÷ 3 = 25
- 25 is divisible by 5: 25 ÷ 5 = 5
- 5 is a prime number
Thus, the prime factorization of 150 is: \( 150 = 2 \times 3 \times 5^2 \)
- Rewrite the Square Root:
Next, we rewrite the square root of 150 using its prime factors:
\(\sqrt{150} = \sqrt{2 \times 3 \times 5^2}\)
- Simplify the Expression:
We can separate the perfect square ( \( 5^2 \) ) from the other factors under the square root:
\(\sqrt{150} = \sqrt{2 \times 3 \times 5^2} = \sqrt{2} \times \sqrt{3} \times \sqrt{5^2}\)
Since the square root of \( 5^2 \) is 5, we can simplify the expression further:
\(\sqrt{150} = \sqrt{2} \times \sqrt{3} \times 5\)
Therefore, the simplified form is:
\(\sqrt{150} = 5\sqrt{6}\)
In conclusion, using the prime factorization method, we have simplified the square root of 150 to \( 5\sqrt{6} \). This method helps in breaking down complex square roots into simpler forms by extracting and simplifying perfect squares from the radical.
Steps to Simplify Square Root of 150
Simplifying the square root of 150 involves expressing it in its simplest radical form. Here are the steps to achieve this:
- Factorize 150 into its prime factors: \(150 = 2 \times 3 \times 5^2\).
- Identify the perfect squares within the factorization. Here, \(5^2\) is a perfect square.
- Rewrite the square root of 150 using the identified perfect square: \(\sqrt{150} = \sqrt{5^2 \times 6} = \sqrt{5^2} \times \sqrt{6}\).
- Take the square root of the perfect square: \(\sqrt{5^2} = 5\).
- Combine the results to express the square root of 150 in its simplest form: \(5\sqrt{6}\).
Thus, the simplified form of the square root of 150 is \(5\sqrt{6}\).
Example Problems
Here are some example problems to help you understand how to simplify the square root of 150 using different methods.
-
Problem 1: Simplify \( \sqrt{150} \)
- Step 1: Factor 150 into prime factors: \( 150 = 2 \times 3 \times 5^2 \)
- Step 2: Identify pairs of factors: \( 5^2 \)
- Step 3: Simplify by taking the square root of the pair: \( \sqrt{150} = 5\sqrt{6} \)
-
Problem 2: Simplify \( \sqrt{75} \)
- Step 1: Factor 75 into prime factors: \( 75 = 3 \times 5^2 \)
- Step 2: Identify pairs of factors: \( 5^2 \)
- Step 3: Simplify by taking the square root of the pair: \( \sqrt{75} = 5\sqrt{3} \)
-
Problem 3: Simplify \( \sqrt{45} \)
- Step 1: Factor 45 into prime factors: \( 45 = 3^2 \times 5 \)
- Step 2: Identify pairs of factors: \( 3^2 \)
- Step 3: Simplify by taking the square root of the pair: \( \sqrt{45} = 3\sqrt{5} \)
These examples illustrate the steps to simplify square roots by breaking down the number into its prime factors, identifying pairs, and simplifying accordingly.
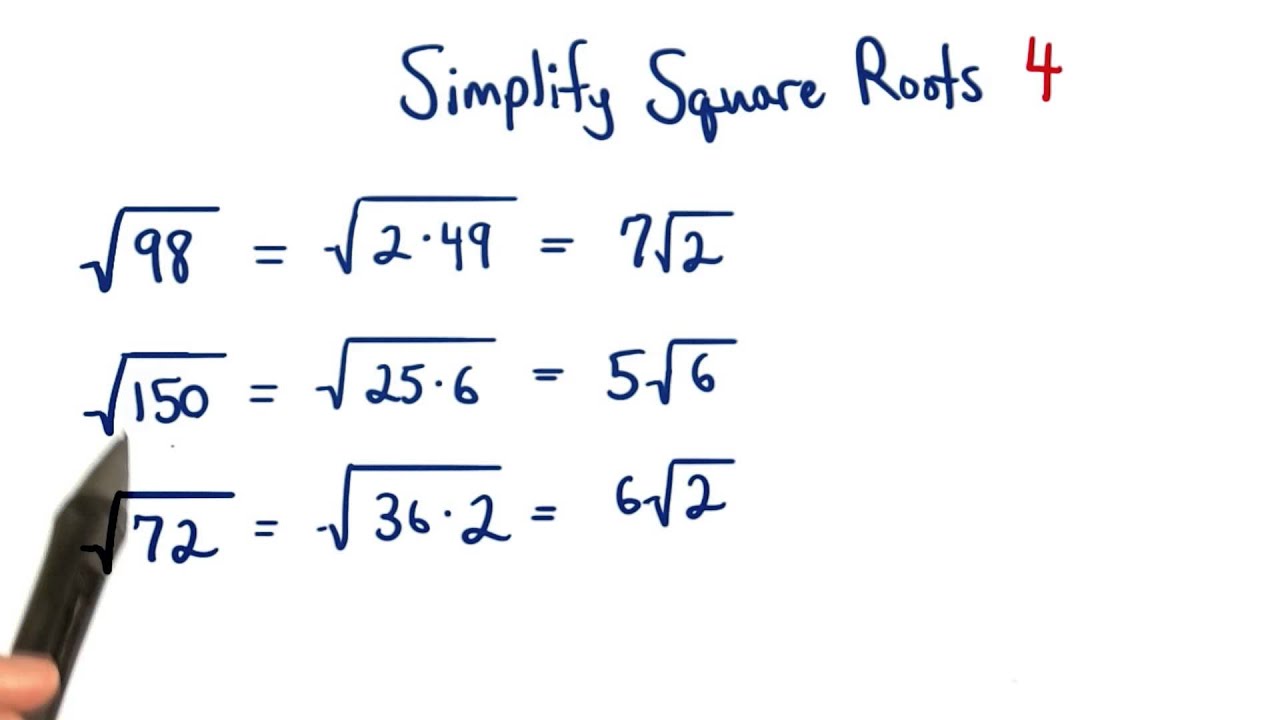
Properties of Square Roots
Understanding the properties of square roots is essential in simplifying and manipulating radical expressions. Below are some fundamental properties:
- Non-Negative Property: The square root of a non-negative number is also non-negative. For example, \( \sqrt{25} = 5 \) and \( \sqrt{0} = 0 \).
- Product Property: The square root of a product is equal to the product of the square roots of the factors. Mathematically, \( \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \). For instance, \( \sqrt{6 \cdot 3} = \sqrt{6} \cdot \sqrt{3} = 3\sqrt{2} \).
- Quotient Property: The square root of a quotient is equal to the quotient of the square roots. This is expressed as \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \). For example, \( \sqrt{\frac{35}{7}} = \frac{\sqrt{35}}{\sqrt{7}} = \sqrt{5} \).
- Even and Odd Properties: The square root of an even perfect square is always even, and the square root of an odd perfect square is always odd. For instance, \( \sqrt{144} = 12 \) (even) and \( \sqrt{225} = 15 \) (odd).
- Irrational Numbers: If a number is not a perfect square, its square root will be irrational. For example, \( \sqrt{23} = 4.79583... \), an irrational number.
- Negative Numbers: The square root of a negative number is imaginary. For instance, \( \sqrt{-9} = 3i \).
These properties help in simplifying complex expressions and solving various mathematical problems involving square roots.
Applications of Simplified Square Roots
Simplified square roots are used in various real-world applications and different fields of study. Understanding how to simplify square roots can make calculations easier and more efficient. Here are some key applications:
- Geometry and Trigonometry:
In geometry, simplified square roots are often used to find the lengths of sides in right triangles, especially when dealing with the Pythagorean theorem. For example, the hypotenuse of a right triangle with legs of length 5 and 5 can be simplified using square roots:
\[\sqrt{5^2 + 5^2} = \sqrt{25 + 25} = \sqrt{50} = 5\sqrt{2}\]
- Engineering:
Engineers frequently use simplified square roots in calculations involving areas, volumes, and other measurements. Simplifying the square root of 150 can make it easier to handle and communicate:
\[\sqrt{150} = \sqrt{25 \times 6} = 5\sqrt{6}\]
- Physics:
In physics, square roots appear in formulas related to motion, energy, and waves. Simplifying these roots can help in understanding and solving physical problems more efficiently. For example, the formula for the period of a simple pendulum involves the square root of the length of the pendulum:
\[T = 2\pi\sqrt{\frac{L}{g}}\]
- Computer Science:
Algorithms in computer science sometimes involve calculations with square roots. Simplified roots can help optimize these algorithms for better performance. For instance, in some graphics algorithms, distances between points are calculated using square roots.
- Statistics:
In statistics, standard deviation and other measures of spread involve square roots. Simplifying these calculations can make statistical analysis more straightforward. For example, the variance of a dataset often requires taking the square root to find the standard deviation.
Overall, mastering the simplification of square roots like \(\sqrt{150} = 5\sqrt{6}\) can be highly beneficial across various disciplines, enabling more efficient and accurate calculations.
Common Mistakes to Avoid
When simplifying square roots, it's important to be aware of some common pitfalls that students often encounter. By understanding these mistakes, you can avoid them and simplify square roots correctly.
-
Not Identifying Perfect Squares:
One of the most frequent mistakes is failing to recognize perfect square factors within the radicand (the number under the square root). For instance, in simplifying \( \sqrt{150} \), it's crucial to notice that 150 can be factored as 25 and 6, where 25 is a perfect square.
-
Incorrectly Breaking Down the Radicand:
Ensure you correctly factor the radicand into its prime factors and identify the largest perfect square. For example, \( 150 = 2 \times 3 \times 5^2 \). From this, \( \sqrt{150} \) simplifies to \( 5\sqrt{6} \) because \( \sqrt{25} = 5 \).
-
Forgetting to Simplify Completely:
After initial simplification, double-check that no further simplification is possible. Simplifying \( \sqrt{50} \) to \( 5\sqrt{2} \) is correct, but always ensure no additional factors can be simplified.
-
Neglecting to Rationalize Denominators:
When dealing with fractions, make sure to rationalize the denominator. For instance, if you have \( \frac{\sqrt{2}}{\sqrt{3}} \), multiply numerator and denominator by \( \sqrt{3} \) to get \( \frac{\sqrt{6}}{3} \).
-
Misapplying the Distributive Property:
Be cautious when applying the distributive property. For example, \( \sqrt{a + b} \neq \sqrt{a} + \sqrt{b} \). Each term inside the square root must be simplified separately unless they can be factored together.
-
Errors with Negative Radicands:
Remember that the square root of a negative number involves imaginary numbers. For example, \( \sqrt{-16} \) simplifies to \( 4i \) where \( i \) is the imaginary unit.
By being mindful of these common mistakes, you can enhance your skills in simplifying square roots and avoid potential errors.
Xem video hướng dẫn cách đơn giản hóa căn bậc hai của 150 để hiểu rõ hơn về quá trình tính toán và áp dụng trong các tình huống thực tế.
Cách Đơn Giản Hóa Căn Bậc Hai của 150: sqrt(150)
READ MORE:
Xem video hướng dẫn cách đơn giản hóa căn bậc hai của 150 để nắm vững phương pháp và ứng dụng trong các bài toán thực tế.
Căn bậc hai của 150 được đơn giản hóa || Hướng dẫn Toán học












