Topic simplified square root of 10: Welcome to our comprehensive guide on the simplified square root of 10. This article delves into the intricacies of square roots, focusing on the unique properties and applications of the square root of 10. Whether you're a student, educator, or math enthusiast, you'll find valuable insights and practical tips to enhance your understanding.
Table of Content
- Understanding the Simplified Square Root of 10
- Introduction to Square Root of 10
- Understanding Irrational Numbers
- Approximating the Square Root of 10
- Methods to Simplify Square Roots
- Prime Factorization of 10
- Why Square Root of 10 Cannot Be Simplified Further
- Approximate Value of Square Root of 10
- Decimal Representation of Square Root of 10
- Using Calculators to Find Square Roots
- Mathematical Properties of Square Root of 10
- Practical Applications of Square Root of 10
- Square Root of 10 in Geometry
- Square Root of 10 in the Pythagorean Theorem
- Comparing Square Root of 10 with Other Square Roots
- Visual Representation of Square Root of 10
- Conclusion on Square Root of 10
- YOUTUBE: Tìm hiểu căn bậc hai của số 10 và cách đơn giản hóa nó. Video này cung cấp các bước chi tiết để giúp bạn hiểu rõ hơn về khái niệm này.
Understanding the Simplified Square Root of 10
The square root of 10 is an irrational number, meaning it cannot be expressed as a simple fraction. It is represented as √10. However, we can approximate its value to better understand it.
Approximation of √10
Using a calculator, we find that:
√10 ≈ 3.162277660168379
This value is an approximation accurate to several decimal places.
Simplifying Square Roots
When simplifying square roots, we look for factors that are perfect squares. However, 10 does not have any factors that are perfect squares, other than 1.
Therefore, the simplified form of √10 remains √10.
Steps to Simplify Square Roots
- Find the prime factors of the number.
- Identify pairs of prime factors.
- Take out each pair of prime factors from under the square root as a single number.
- Multiply the numbers outside the square root.
- Multiply the numbers inside the square root.
Since 10 = 2 × 5 and neither 2 nor 5 is a perfect square, we cannot simplify √10 further.
Practical Applications
The square root of 10 appears in various mathematical contexts, such as in geometry when dealing with right triangles and the Pythagorean theorem.
Conclusion
While √10 cannot be simplified further, understanding its approximate value and the method for simplifying square roots can be very useful in many mathematical problems.
| Symbol | Value |
| √10 | ≈ 3.162277660168379 |

READ MORE:
Introduction to Square Root of 10
The square root of 10, denoted as \( \sqrt{10} \), is an important mathematical concept that finds application in various fields. It is classified as an irrational number, meaning it cannot be expressed as a simple fraction. In this section, we will explore the fundamental aspects of the square root of 10.
Here are some key points to understand about \( \sqrt{10} \):
- The square root of 10 is approximately equal to 3.16227766017.
- It is an irrational number, so its decimal representation is non-repeating and non-terminating.
- The square root of 10 can be found using methods such as long division, approximation, or a calculator.
Let's delve deeper into the properties and significance of \( \sqrt{10} \).
- Irrational Number: The square root of 10 cannot be expressed as a fraction of two integers. This irrationality implies a complex decimal expansion.
- Approximations: While \( \sqrt{10} \) cannot be simplified to a smaller integer, its value can be approximated using various techniques. For instance, \( \sqrt{10} \approx 3.162 \).
- Methods to Find:
- Long Division: A manual method to approximate square roots.
- Calculator: The most efficient and accurate method for most purposes.
Understanding the square root of 10 is crucial for its application in geometry, algebra, and beyond. Whether calculating areas, solving equations, or understanding the properties of numbers, \( \sqrt{10} \) plays a significant role.
Understanding Irrational Numbers
Irrational numbers are a fascinating class of numbers that cannot be expressed as a simple fraction of two integers. They have unique properties and play a significant role in various branches of mathematics. An irrational number's decimal expansion is non-repeating and non-terminating, making it impossible to represent exactly as a fraction.
Here are some key characteristics of irrational numbers:
- Non-repeating Decimal: The decimal expansion of an irrational number does not repeat. For example, \( \sqrt{10} \approx 3.16227766017 \ldots \) continues indefinitely without a repeating pattern.
- Non-terminating Decimal: Unlike rational numbers, irrational numbers do not terminate. Their decimal form goes on forever.
- Cannot be Expressed as a Fraction: There are no two integers \(a\) and \(b\) such that \( \frac{a}{b} \) equals an irrational number. For example, \( \sqrt{10} \) cannot be written as a fraction of two integers.
To further understand irrational numbers, let's consider their properties and examples:
- Square Roots: Many square roots of non-perfect squares are irrational. For instance, \( \sqrt{2} \), \( \sqrt{3} \), and \( \sqrt{10} \) are all irrational.
- Pi ( \( \pi \) ): The number \( \pi \), representing the ratio of a circle's circumference to its diameter, is another famous irrational number.
- Euler's Number ( \( e \) ): The base of natural logarithms, \( e \), is an irrational number widely used in calculus and complex analysis.
Irrational numbers are essential in mathematical theories and real-world applications. Their unique properties enable precise calculations in geometry, trigonometry, and calculus, contributing to advancements in science and engineering.
Approximating the Square Root of 10
Approximating the square root of 10, \( \sqrt{10} \), involves finding a value that is close to the actual square root. Since \( \sqrt{10} \) is an irrational number, its exact value cannot be determined, but we can get close through various methods. Here, we explore different techniques for approximation.
One common method is using a calculator, but manual methods provide a deeper understanding of the process. Let's look at a few methods:
- Long Division Method: This traditional method can provide a precise approximation by following these steps:
- Pair the digits of the number starting from the decimal point. For 10, we write it as 10.00 00.
- Find the largest number whose square is less than or equal to the first pair. Here, it's 3 because \( 3^2 = 9 \).
- Subtract the square from the first pair and bring down the next pair of digits (10 - 9 = 1, bring down 00 to get 100).
- Double the quotient (3) to get 6, then find a digit \( x \) such that \( 6x \cdot x \) is less than or equal to 100. Here, \( x = 1 \) since \( 61 \times 1 = 61 \).
- Repeat the process to get more decimal places.
- Using Newton's Method: Also known as the Heron's method, this iterative approach refines the approximation:
- Start with an initial guess, \( x_0 \). For \( \sqrt{10} \), a good starting point might be 3.
- Apply the formula \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{10}{x_n} \right) \).
- Repeat until the desired precision is reached.
- Using a Calculator: The simplest and quickest way to approximate \( \sqrt{10} \):
- Enter 10 and press the square root function.
- The calculator provides an approximation, typically to several decimal places. For example, \( \sqrt{10} \approx 3.16227766017 \).
By employing these methods, you can approximate the square root of 10 with varying degrees of accuracy. Understanding these techniques enhances your mathematical skills and provides insights into the nature of irrational numbers.
Methods to Simplify Square Roots
Simplifying square roots involves expressing the square root in its simplest form. While some square roots cannot be simplified further, the process of simplification helps in understanding the properties of square roots and making calculations easier. Here, we will discuss several methods to simplify square roots step by step.
Let's consider a general square root \( \sqrt{a} \), where \( a \) is a positive integer.
- Prime Factorization Method:
- Find the prime factorization of the number \( a \).
- Group the prime factors in pairs.
- Move one factor from each pair outside the square root.
- If any factors are not paired, they remain inside the square root.
For example, to simplify \( \sqrt{72} \):
- Prime factorization of 72: \( 72 = 2 \times 2 \times 2 \times 3 \times 3 \).
- Grouping in pairs: \( 72 = (2 \times 2) \times (3 \times 3) \times 2 \).
- Taking one factor from each pair: \( \sqrt{72} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2} \).
- Simplifying Square Roots of Non-Perfect Squares:
When dealing with non-perfect squares, it's important to identify if the number has any perfect square factors.
- For example, \( \sqrt{50} \) can be simplified by recognizing that 50 is \( 25 \times 2 \).
- Since \( 25 \) is a perfect square, we can write \( \sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} = 5\sqrt{2} \).
- Using the Property of Square Roots:
Utilize the property \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \) to break down the square root into simpler parts.
- For instance, \( \sqrt{18} = \sqrt{9 \times 2} = \sqrt{9} \times \sqrt{2} = 3\sqrt{2} \).
In the case of the square root of 10, \( \sqrt{10} \), it cannot be simplified further because 10 does not have any perfect square factors. Therefore, \( \sqrt{10} \) remains in its simplest form.

Prime Factorization of 10
Prime factorization involves breaking down a number into its prime factors. This process is fundamental in simplifying square roots and understanding the properties of numbers. Let's explore the prime factorization of 10 and its implications.
Here are the steps to find the prime factorization of 10:
- Identify the smallest prime number:
The smallest prime number is 2. Check if 10 is divisible by 2.
- Since 10 is an even number, it is divisible by 2.
- Divide the number by the prime number:
Divide 10 by 2 to get 5.
- \( 10 \div 2 = 5 \)
- Check if the result is a prime number:
Determine if the quotient, 5, is a prime number.
- 5 is a prime number because it is only divisible by 1 and itself.
Thus, the prime factorization of 10 is:
\( 10 = 2 \times 5 \)
This prime factorization helps in understanding the composition of the number 10. Each factor, 2 and 5, is a prime number, meaning they cannot be broken down further into other integers.
In the context of simplifying the square root of 10, the prime factorization shows that \( \sqrt{10} \) cannot be simplified because neither 2 nor 5 is a perfect square. Therefore, \( \sqrt{10} \) remains in its simplest form.
Why Square Root of 10 Cannot Be Simplified Further
Understanding why the square root of 10, \( \sqrt{10} \), cannot be simplified further requires a look into its prime factorization and properties of square roots. Simplifying a square root involves expressing it in terms of smaller, perfect squares, but this is not possible for \( \sqrt{10} \).
Here are the detailed reasons:
- Prime Factorization:
The prime factorization of 10 is:
\( 10 = 2 \times 5 \)
Both 2 and 5 are prime numbers. To simplify a square root, we look for pairs of prime factors. However, since 10 is composed of two distinct prime numbers with no pairs, it cannot be simplified.
- No Perfect Square Factors:
For a square root to be simplified, the number must have factors that are perfect squares. Perfect squares are numbers like 1, 4, 9, 16, etc., which can be expressed as \( n^2 \). Since 10 does not have any perfect square factors other than 1, it remains unsimplified.
- Irrational Number:
The square root of 10 is an irrational number, meaning it cannot be expressed as a simple fraction or a terminating or repeating decimal. Its decimal form is non-repeating and non-terminating:
\( \sqrt{10} \approx 3.16227766017 \ldots \)
This irrational nature indicates that \( \sqrt{10} \) does not simplify neatly into a rational number.
In summary, the square root of 10 cannot be simplified further because its prime factorization does not contain pairs of primes, it lacks perfect square factors, and it is inherently an irrational number. Therefore, \( \sqrt{10} \) remains in its simplest form as \( \sqrt{10} \).
Approximate Value of Square Root of 10
The square root of 10, \( \sqrt{10} \), is an irrational number, which means its exact value cannot be represented as a simple fraction or a finite decimal. However, we can approximate its value to a high degree of accuracy. Here, we explore different methods to approximate \( \sqrt{10} \).
Here are some steps to find the approximate value of \( \sqrt{10} \):
- Using a Calculator:
- The most straightforward method is to use a scientific calculator. By entering 10 and pressing the square root function, the calculator provides the approximation:
- \( \sqrt{10} \approx 3.16227766017 \)
- Long Division Method:
This manual method involves a series of steps to find the square root to a desired decimal place:
- Pair the digits of 10 starting from the decimal point: 10.00 00 00.
- Find the largest integer whose square is less than or equal to the first pair (10). Here, it is 3, since \( 3^2 = 9 \).
- Subtract the square from the first pair and bring down the next pair of digits: \( 10 - 9 = 1 \), bring down 00 to get 100.
- Double the quotient (3) to get 6, and find a digit \( x \) such that \( 60x \times x \) is less than or equal to 100. Here, \( x = 1 \) since \( 61 \times 1 = 61 \).
- Repeat the process with the remainder (100 - 61 = 39) and bring down the next pair to continue.
- Newton's Method:
Also known as the Heron's method, this iterative technique refines the approximation:
- Start with an initial guess, \( x_0 \). For \( \sqrt{10} \), a good starting point might be 3.
- Apply the formula \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{10}{x_n} \right) \).
- Repeat the process until the difference between \( x_n \) and \( x_{n+1} \) is within the desired precision.
For example, starting with \( x_0 = 3 \):
- First iteration: \( x_1 = \frac{1}{2} \left( 3 + \frac{10}{3} \right) = 3.1667 \)
- Second iteration: \( x_2 = \frac{1}{2} \left( 3.1667 + \frac{10}{3.1667} \right) = 3.1623 \)
- Continuing this process yields a more accurate approximation.
By using these methods, we can approximate \( \sqrt{10} \) as 3.162, 3.1623, or even more precisely, depending on the level of accuracy required.
Decimal Representation of Square Root of 10
The square root of 10, \( \sqrt{10} \), is an irrational number, which means its decimal representation is non-terminating and non-repeating. This makes it impossible to express exactly, but we can represent it to a high degree of precision. Here, we explore the decimal representation of \( \sqrt{10} \) step by step.
Using a calculator, the square root of 10 is approximately:
\( \sqrt{10} \approx 3.16227766017 \ldots \)
Let's delve into the steps of finding this decimal representation:
- Long Division Method:
This manual method provides a way to approximate the square root to several decimal places:
- Pair the digits of the number starting from the decimal point: 10.00 00 00.
- Find the largest number whose square is less than or equal to the first pair (10). Here, it's 3, because \( 3^2 = 9 \).
- Subtract the square from the first pair and bring down the next pair: \( 10 - 9 = 1 \), bring down 00 to get 100.
- Double the quotient (3) to get 6, then find a digit \( x \) such that \( 60x \times x \leq 100 \). Here, \( x = 1 \) since \( 61 \times 1 = 61 \).
- Continue the process with the remainder (100 - 61 = 39) and bring down the next pair to continue: 3900.
- Repeat the steps to get more decimal places. The process yields more digits as needed.
- Newton's Method:
This iterative method provides an increasingly accurate approximation:
- Start with an initial guess, \( x_0 \). For \( \sqrt{10} \), a good starting point is 3.
- Apply the formula \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{10}{x_n} \right) \).
- Repeat the process until the values stabilize to the desired precision.
For instance, starting with \( x_0 = 3 \):
- First iteration: \( x_1 = \frac{1}{2} \left( 3 + \frac{10}{3} \right) = 3.1667 \)
- Second iteration: \( x_2 = \frac{1}{2} \left( 3.1667 + \frac{10}{3.1667} \right) = 3.1623 \)
- Further iterations refine this value.
- Using a Calculator:
Most scientific calculators can quickly provide the decimal representation of \( \sqrt{10} \). Simply enter the number and press the square root button to get the approximation:
\( \sqrt{10} \approx 3.16227766017 \ldots \)
The decimal representation of \( \sqrt{10} \) is infinite and non-repeating, demonstrating its irrational nature. By using these methods, you can approximate \( \sqrt{10} \) to as many decimal places as needed for practical applications.

Using Calculators to Find Square Roots
Calculators are powerful tools that simplify the process of finding square roots, providing quick and accurate results. Here's a detailed guide on how to use calculators to find the square root of a number, specifically focusing on \( \sqrt{10} \).
Follow these steps to find the square root using a calculator:
- Turn on the Calculator:
Ensure your calculator is powered on. For scientific and graphing calculators, this typically involves pressing the power button.
- Input the Number:
Enter the number for which you want to find the square root. For example, to find \( \sqrt{10} \), simply press the number 10 on the keypad.
- Locate the Square Root Function:
Most calculators have a square root button, often labeled as \( \sqrt{x} \) or with a radical symbol (√). This button is usually found among the function keys.
- On a standard scientific calculator, it might be a primary or secondary function. If it's a secondary function, you might need to press the "Shift" or "2nd" key first.
- Press the Square Root Button:
After entering the number 10, press the square root button. The calculator will then display the square root of 10.
The display should show: \( \sqrt{10} \approx 3.16227766017 \).
- Interpret the Result:
Understand that the result is an approximation of the square root, accurate to the number of decimal places your calculator can display. Most scientific calculators show at least 10 decimal places.
Using calculators not only speeds up the process of finding square roots but also ensures accuracy, which is particularly useful in complex calculations and practical applications.
Additionally, some advanced calculators and software tools offer more functionalities:
- Graphing Calculators: These can plot functions and visually display the square root values on graphs, providing a deeper understanding of their behavior.
- Online Calculators and Apps: Many websites and mobile apps offer square root functions, often with additional features like step-by-step solutions and educational explanations.
By leveraging these tools, you can easily and accurately find the square roots of any number, including the simplified square root of 10.
Mathematical Properties of Square Root of 10
The square root of 10, denoted as \( \sqrt{10} \), is an irrational number. This means it cannot be expressed as a simple fraction, and its decimal representation is non-terminating and non-repeating. Here are some key mathematical properties of \( \sqrt{10} \):
- Irrationality: \( \sqrt{10} \) cannot be written as a ratio of two integers. Its decimal expansion is infinite and non-repeating.
- Decimal Approximation: The approximate value of \( \sqrt{10} \) is 3.162277660168379. For practical purposes, it is often rounded to 3.16 or 3.162.
- Algebraic Properties: \( \sqrt{10} \) satisfies the equation \( x^2 = 10 \).
- Continuity: As a function, \( \sqrt{10} \) is continuous and differentiable, meaning it has no breaks or holes in its graph.
- Comparison with Integers: Since \( \sqrt{9} = 3 \) and \( \sqrt{16} = 4 \), \( \sqrt{10} \) lies between 3 and 4.
Let's explore some additional mathematical aspects of \( \sqrt{10} \):
| Property | Explanation |
|---|---|
| Square | \( (\sqrt{10})^2 = 10 \) |
| Reciprocal | \( \frac{1}{\sqrt{10}} = \frac{\sqrt{10}}{10} \approx 0.316 \) |
| Exponentiation | \( \sqrt{10}^n = 10^{n/2} \) for any real number \( n \) |
In trigonometry and geometry, \( \sqrt{10} \) often appears in various formulas and calculations. For example:
- In the Pythagorean theorem, it can represent the hypotenuse of a right triangle with legs of lengths \( \sqrt{5} \) and \( \sqrt{5} \), as \( \sqrt{5^2 + 5^2} = \sqrt{10} \).
- It is used to calculate distances in the coordinate plane and in three-dimensional space.
The number \( \sqrt{10} \) also exhibits interesting behavior in calculus:
- The derivative of \( f(x) = \sqrt{x} \) at \( x = 10 \) is \( f'(10) = \frac{1}{2\sqrt{10}} \).
- The integral of \( f(x) = \sqrt{x} \) from 0 to 10 is \( \int_0^{10} \sqrt{x} \, dx = \frac{2}{3} \cdot 10^{3/2} = \frac{20\sqrt{10}}{3} \).
Practical Applications of Square Root of 10
The square root of 10, approximately 3.162, has various practical applications in different fields. Here are some significant uses:
- Engineering and Physics:
In engineering and physics, the square root of 10 is often used in calculations involving the design and analysis of systems. For example, it can be used in determining the lengths of diagonals in rectangular structures or calculating the magnitudes of vectors.
- Geometry:
In geometry, the square root of 10 can be used to find the diagonal of a rectangle. For a rectangle with side lengths of 1 and 3, the diagonal \(d\) can be calculated using the Pythagorean theorem:
\[
d = \sqrt{1^2 + 3^2} = \sqrt{1 + 9} = \sqrt{10}
\] - Astronomy:
Astronomers may use the square root of 10 in various calculations, such as determining distances between celestial objects. The square root of 10 is also relevant in formulas that describe the scaling of distances or sizes in the universe.
- Statistics:
In statistics, the square root of 10 can appear in formulas for standard deviations or variances. For instance, if the variance of a dataset is 10, the standard deviation is the square root of the variance:
\[
\sigma = \sqrt{10}
\] - Finance:
In finance, the square root of 10 can be used in the context of risk management and investment. For example, it may appear in calculations of volatility or in the assessment of the standard deviation of investment returns.
Overall, the square root of 10 is a valuable mathematical constant that plays a crucial role in various scientific, engineering, and mathematical applications.
Square Root of 10 in Geometry
The square root of 10, denoted as \( \sqrt{10} \), has significant applications in geometry, particularly in solving problems involving right triangles, distances, and certain geometric constructions. Here are some practical examples:
-
Right Triangles: In right triangles, the Pythagorean theorem is frequently used to find the length of sides. For example, in a right triangle where one leg is 1 and the hypotenuse is \( \sqrt{10} \), the other leg can be found as follows:
Given: \( a^2 + b^2 = c^2 \)
\( 1^2 + b^2 = (\sqrt{10})^2 \)
\( 1 + b^2 = 10 \)
\( b^2 = 9 \)
\( b = 3 \)
Thus, the other leg of the triangle is 3.
-
Distance Between Points: In coordinate geometry, the distance between two points \((x_1, y_1)\) and \((x_2, y_2)\) is given by:
\( d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \)
For instance, the distance between points (0, 0) and (3, 1) is:
\( d = \sqrt{(3 - 0)^2 + (1 - 0)^2} = \sqrt{9 + 1} = \sqrt{10} \)
This shows that the distance between these two points is \( \sqrt{10} \).
-
Circle Radius and Area: If a circle has an area of 10 square units, the radius can be found using the formula for the area of a circle, \( A = \pi r^2 \).
\( 10 = \pi r^2 \)
\( r^2 = \frac{10}{\pi} \)
\( r = \sqrt{\frac{10}{\pi}} \)
Thus, the radius of the circle is \( \sqrt{\frac{10}{\pi}} \).
-
Geometric Constructions: The length \( \sqrt{10} \) can be used in geometric constructions involving irrational numbers, for example, constructing a right triangle with sides of known lengths to approximate \( \sqrt{10} \).
These examples demonstrate the importance and utility of \( \sqrt{10} \) in various geometric contexts, providing a practical understanding of its application beyond theoretical mathematics.

Square Root of 10 in the Pythagorean Theorem
The Pythagorean Theorem is a fundamental principle in geometry that relates the lengths of the sides of a right triangle. It states that the square of the hypotenuse (\(c\)) is equal to the sum of the squares of the other two sides (\(a\) and \(b\)):
\(a^2 + b^2 = c^2\)
To explore the application of the square root of 10 in the Pythagorean Theorem, consider a right triangle where one of the legs is \( \sqrt{10} \). This example demonstrates how the theorem can be used to find unknown side lengths:
- Example 1: Right Triangle with sides \( \sqrt{10} \) and 3
- Given sides: \( a = \sqrt{10} \) and \( b = 3 \)
- Apply the Pythagorean Theorem: \( a^2 + b^2 = c^2 \)
- Substitute the known values: \( (\sqrt{10})^2 + 3^2 = c^2 \)
- Simplify: \( 10 + 9 = c^2 \)
- Combine terms: \( 19 = c^2 \)
- Solve for \( c \): \( c = \sqrt{19} \)
Thus, the hypotenuse \( c \) of the triangle is \( \sqrt{19} \).
- Example 2: Right Triangle with hypotenuse \( \sqrt{10} \)
- Given: Hypotenuse \( c = \sqrt{10} \) and one leg \( a = 2 \)
- Apply the Pythagorean Theorem: \( a^2 + b^2 = c^2 \)
- Substitute the known values: \( 2^2 + b^2 = (\sqrt{10})^2 \)
- Simplify: \( 4 + b^2 = 10 \)
- Isolate \( b^2 \): \( b^2 = 10 - 4 \)
- Solve for \( b \): \( b^2 = 6 \)
- Final result: \( b = \sqrt{6} \)
Therefore, the other leg \( b \) of the triangle is \( \sqrt{6} \).
These examples show how the square root of 10 can be used in the context of the Pythagorean Theorem to determine the lengths of sides in a right triangle. Understanding and applying this relationship allows for solving a variety of geometric problems.
Comparing Square Root of 10 with Other Square Roots
The square root of 10, approximately \(3.162\), can be compared to other square roots to understand its relative magnitude and properties. Here is a detailed comparison with various other square roots:
- Square Root of 2: \( \sqrt{2} \approx 1.414 \)
- Smaller than \( \sqrt{10} \)
- Commonly appears in geometric contexts, such as the diagonal of a square with unit side length.
- Square Root of 3: \( \sqrt{3} \approx 1.732 \)
- Smaller than \( \sqrt{10} \)
- Occurs in the geometry of equilateral triangles (height calculation).
- Square Root of 5: \( \sqrt{5} \approx 2.236 \)
- Smaller than \( \sqrt{10} \)
- Appears in the golden ratio, \( \phi = \frac{1 + \sqrt{5}}{2} \).
- Square Root of 10: \( \sqrt{10} \approx 3.162 \)
- Larger than \( \sqrt{2}, \sqrt{3}, \) and \( \sqrt{5} \)
- Often used in statistical calculations and standard deviations.
- Square Root of 16: \( \sqrt{16} = 4 \)
- Larger than \( \sqrt{10} \)
- A perfect square, often seen in simple geometric shapes like squares and circles.
- Square Root of 20: \( \sqrt{20} \approx 4.472 \)
- Larger than \( \sqrt{10} \)
- Can be simplified as \( 2\sqrt{5} \), showing a relationship with \( \sqrt{5} \).
To summarize, the square root of 10 is an irrational number that is larger than the square roots of 2, 3, and 5, but smaller than the square roots of 16 and 20. It often appears in various mathematical and scientific contexts where approximate values are sufficient.
For a visual comparison, consider the following table:
| Number | Square Root | Approximate Value |
|---|---|---|
| 2 | \( \sqrt{2} \) | 1.414 |
| 3 | \( \sqrt{3} \) | 1.732 |
| 5 | \( \sqrt{5} \) | 2.236 |
| 10 | \( \sqrt{10} \) | 3.162 |
| 16 | \( \sqrt{16} \) | 4.000 |
| 20 | \( \sqrt{20} \) | 4.472 |
Visual Representation of Square Root of 10
Visualizing the square root of 10 helps to understand its approximate value and its place among other numbers. Here are a few ways to visually represent and conceptualize the square root of 10:
-
Number Line Representation: Place the square root of 10 on a number line between 3 and 4. Since √9 = 3 and √16 = 4, √10 lies slightly above 3.1 but below 3.2.

-
Square Representation: Draw a square with an area of 10 square units. The length of each side of this square will be √10 units.
10 To better visualize, the side length of this square is about 3.162 units (since √10 ≈ 3.162).
-
Geometric Construction: You can construct a right triangle where one side is 1 unit and the hypotenuse is √10 units. By the Pythagorean theorem, if the other side of the triangle is 3 units, then:
12 + 32 = 1 + 9 = 10
So, the hypotenuse = √10.

These visual methods help to provide a concrete understanding of the square root of 10, emphasizing its approximate value and geometric significance.
Conclusion on Square Root of 10
The square root of 10, denoted as √10, is an irrational number approximately equal to 3.162. It cannot be simplified further into a rational number because it does not have a perfect square factorization. This intrinsic property arises from its prime factorization of 2 and 5, neither of which form a complete pair of squares.
Despite its inability to be simplified into a smaller radical form, the square root of 10 holds significant value in various mathematical contexts. For instance, it plays a crucial role in geometry, where it can be used to calculate diagonal distances in rectangular shapes and other geometric figures. Its practical applications extend to fields like engineering and physics, where precise calculations often require the use of √10.
Using a calculator, √10 can be approximated to several decimal places, offering a more practical value for real-world applications. This approximation is crucial for calculations in scientific experiments and engineering designs, ensuring accuracy and reliability.
To summarize, the square root of 10, though not simplifiable, is a vital mathematical constant with extensive applications in both theoretical and practical realms. Its irrational nature exemplifies the beauty and complexity of mathematics, where even seemingly simple numbers can reveal profound insights and utility.
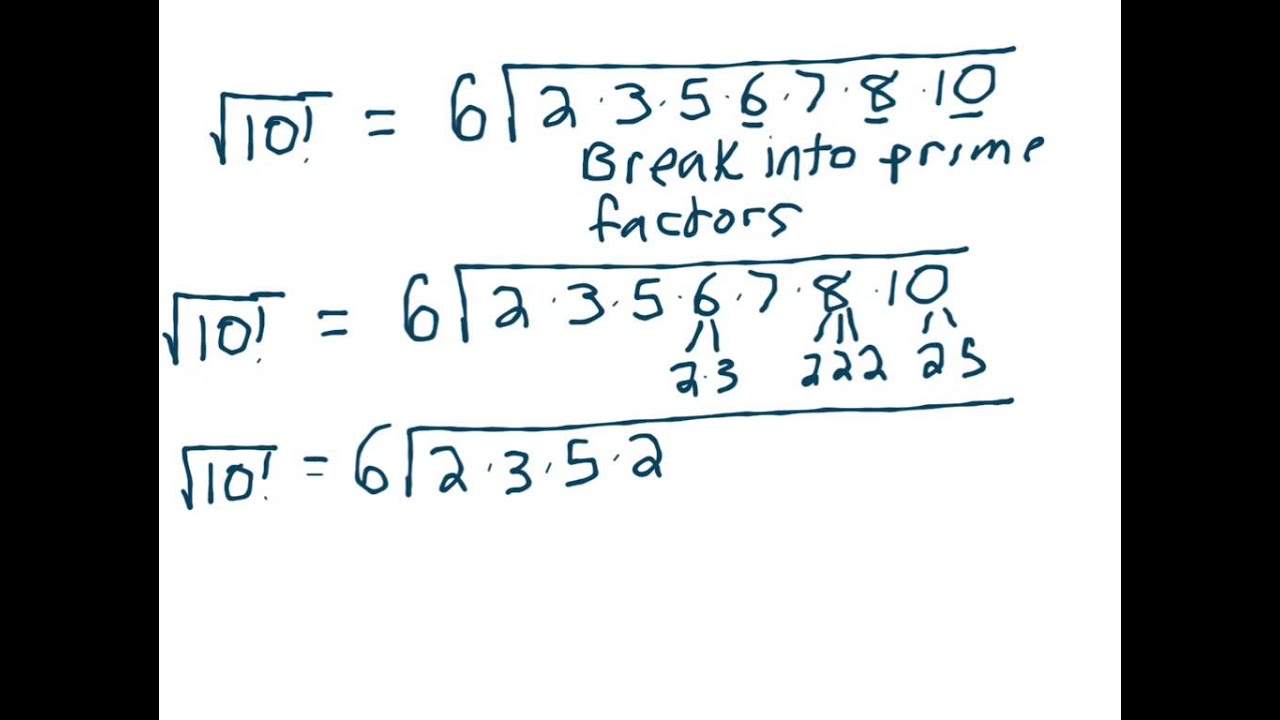
Tìm hiểu căn bậc hai của số 10 và cách đơn giản hóa nó. Video này cung cấp các bước chi tiết để giúp bạn hiểu rõ hơn về khái niệm này.
Căn bậc hai của số 10










